随机运动导电粒子对微波腔内电场分布的影响

（天津科技大学机械工程学院，天津 300222）

（天津科技大学机械工程学院，天津 300222）

针对微波腔内不均匀电磁场导致的微波加热不均匀现象，利用金属对微波具有反射的特点，将导电粒子与运动物料相结合，研究了随机运动导电粒子对微波转筒干燥腔内电场分布的影响.利用EDEM与COMSOL软件将运动场与电磁场相耦合，模拟导电粒子的尺寸、数量以及随机运动方式对微波腔内电场分布的影响.结果表明：直径小于20，mm的导电粒子对电场的影响较小；自由随机运动的导电粒子因粒子集聚而恶化微波腔内的电场分布；固定间距的随机运动导电粒子可提高微波腔内的平均电场强度及电场分布的均匀性.

微波加热；均匀性；回转运动；导电粒子；电场

微波加热由于其加热速度快及选择性加热等特点，在食品、化工、材料、陶瓷及废弃物处理中受到广泛的应用［1-5］.但在工业应用中，微波加热的不均匀性导致产品因局部过热而降低品质以及因局部冷点不能完全杀死微生物而存在食品安全问题［6-9］.因此，提高微波加热的均匀性是研究人员在微波加热应用中需主要解决的问题.Vadivambal等［10］综述了微波加热食品的不均匀现象及影响因素.Li等［11］对微波加热产生不均匀的原因及改善均匀性的措施进行了综述.由于加热不均匀主要由微波腔内不均匀的电磁场和物料的特性（形状、大小、位置、湿含量分布及介电特性）引起，因此，解决不均匀的措施主要包括改善微波腔内电磁场分布的均匀性及物料对微波能吸收的均匀性.其中，微波腔内电磁场的均匀性主要取决于微波腔内模式的数量，模式越多，电磁场分布越均匀.目前，利用模式搅拌器［12-14］、改变微波频率［15］、采用脉动微波［16-17］及微波辐射器［18-19］等均可提高微波腔内电磁场分布的均匀性.另外，利用金属对电磁场反射的特点，Ho等［20］用金属带改善食品温度分布的均匀性，Itaya等［21］在流化床中加入导电粒子改善微波腔内的电磁场分布.Wang等［22］研究了矩形微波腔内放置导电粒子对电磁场分布的影响.研究发现：合理的放置导电粒子可以增大腔内的电场强度和提高电场分布的均匀性.但在应用中导电粒子的放置位置难以直接确定，其放置方式也会受到限制.

本文将导电粒子和运动物料相结合，研究随机运动导电粒子对微波转筒干燥装置内电场分布均匀性的影响.研究中采用EDEM和COMSOL软件分别模拟导电粒子在转筒内的随机运动和矩形微波腔内的电场分布，主要研究导电粒子的尺寸、数量及随机运动方式对微波转筒腔内电场强度及电场分布均匀性的影响.

1 材料与方法

1.1 微波转筒干燥装置

微波转筒干燥装置为在 330，mm×300，mm× 210，mm的矩形微波腔内放置直径为 150，mm、长度为 200，mm的水平回转圆筒，其几何模型见图 1.在转筒内部分布有 6个与轴平行的宽度为 20，mm、厚度为4，mm的抄板.模拟中选择水平转筒的材质为有机玻璃，其物性参数见表 1.微波炉的馈口激励通过矩形波导发射，频率为2.45，GHz，模式为TE10.

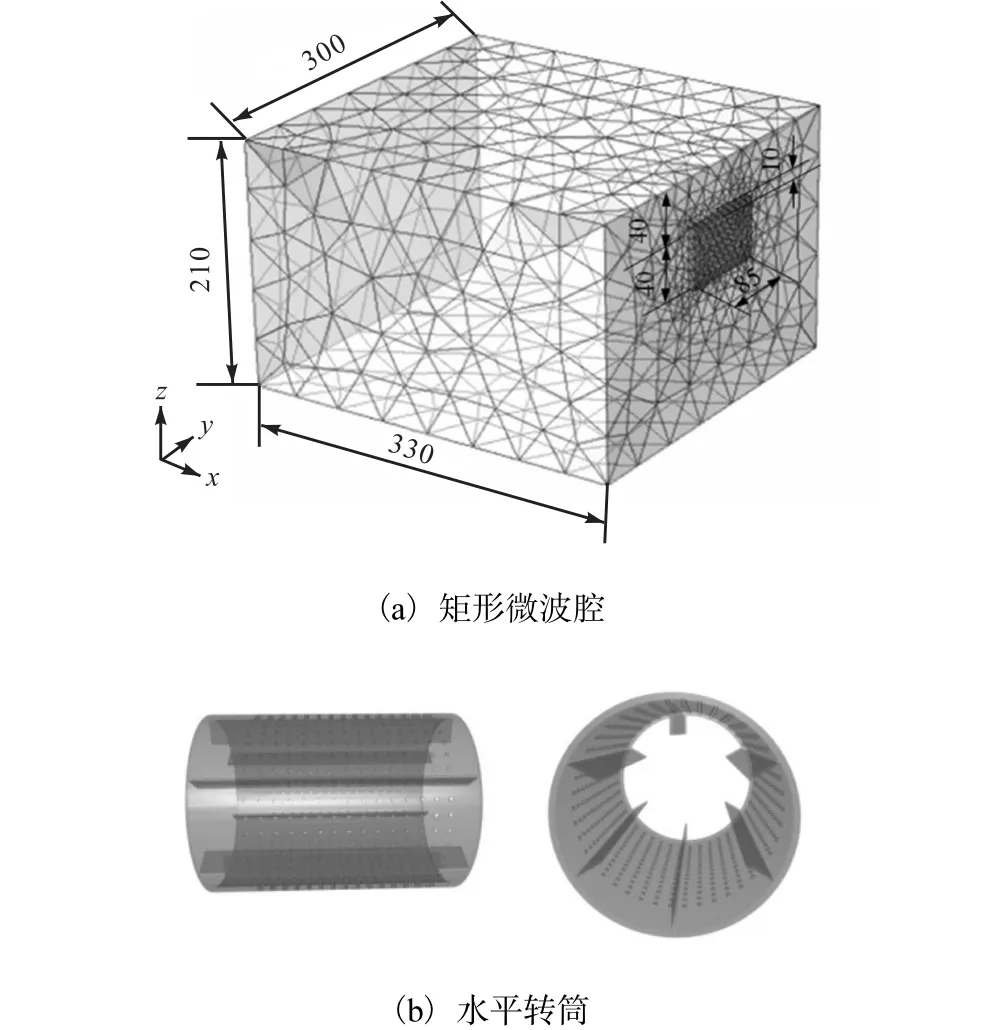
图1 微波转筒干燥装置几何模型Fig. 1 Microwave rotary drying device

表1 有机玻璃的物性参数Tab. 1 Physical properties of plexiglass

1.2 模拟物料

本文主要研究微波转筒干燥大豆时，置于转筒内随机运动的导电粒子对微波转筒腔内电场分布的影响.因此，模拟物料为大豆，导电粒子为金属球.大豆颗粒的物性见表 2.模拟中大豆颗粒的三轴径尺寸分别为长l=7.47，mm，宽b=7.17，mm，高h= 6.63，mm.在EDEM中根据多球产生不同形状颗粒的方法生成颗粒模型如图2所示.在模拟中，假设导电粒子表面为完美电导体，因此导电粒子的材料对模拟没有影响.为避免金属尖角，粒子为圆球形颗粒.

表2 大豆颗粒的物性Tab. 2 Physical properties of soybean particles

图2 大豆颗粒模型Fig. 2 Soybean particle model

2 数学模型

为研究转筒内随机运动导电粒子对微波腔内电场分布的影响，首先利用 EDEM 软件，采用 Hertz-Mindlin接触模型跟踪颗粒群中导电粒子在运动过程中的位置，然后利用 COMSOL软件，通过求解Maxwell方程获得微波腔内电磁场分布.物料（大豆）没有磁性，因此，只对电场强度进行了研究.其控制方程、边界条件及电场分布均匀性评价指标分别为式（1）、式（2）和式（3）.

2.1 控制方程

微波腔内的电场分布通过Maxwell方程求解

式中：μr为相对磁导率；E为电场强度，V/m；k0为波数，m-1；εr为相对介电常数；ε0为真空中的介电常数，F/m；ω为角频率，rad/s；σ为电导率，S/m.

2.2 边界条件

由于导电粒子表面、微波腔及波导内壁面均假设为完美电导体，由 Faraday定律和 Gauss理论［23］可知，沿着所有壁面的电场切向分量均为0，即

2.3 电场分布均匀性评价指标

电场分布的均匀性由变动系数（COV）进行评价，其定义为

式中：Ei和分别为每个取样点的电场强度和平均电场强度，V/m.COV越小表示电场分布越均匀.

3 结果与分析

文献［24］对本装置转筒的装载量及转速对大豆粒子随机运动和混合的影响进行了研究，当装载量为10%时，颗粒的随机性和混合性较好.本文取大豆装载量为10%，转筒转速为15，r/min，通过EDEM模拟与大豆混合的导电粒子在转筒内的随机运动，再利用COMSOL模拟导电粒子在随机运动过程中对微波转筒腔内电场分布的影响.研究中没有考虑大豆颗粒对电场的影响.

3.1 导电粒子尺寸对微波转筒腔内电场分布的影响

由文献［22］可知，在微波腔内放入一个导电粒子，粒径为20，mm时对电场强度的影响较大，故本文以3个20，mm的导电粒子在转筒中的随机运动位置作为COMSOL中不同粒径导电粒子的建模位置.图3为转筒运动至600，s时导电粒子的位置分布图.

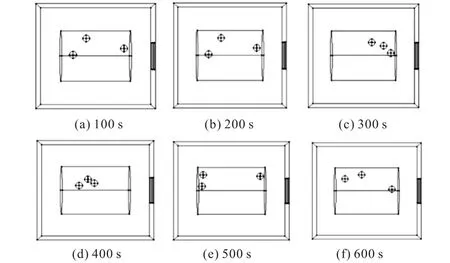
图3 随机运动导电粒子位置（d=20，mm，n=3）Fig. 3 Positions of electrically conductive beads at different time（d=20，mm，n=3）

图 4为导电粒子（d=20，mm，n=3）在运动过程中对微波腔内电场分布的影响，图中三角符号分别表示在该时刻电场强度的最大值和最小值.

图4 随机运动导电粒子对电场强度的影响（xy截面，z= 45，mm，d=20，mm，n=3）Fig. 4 Effect of electrically conductive beads on electric field intensity at different time（xy section，z= 45，mm，d=20，mm，n=3）

图 5反映了导电粒子粒径（d=5、16、20，mm）对电场分布均匀性的影响.

图5 导电粒子粒径对电场分布均匀性的影响（n=3）Fig. 5 Effectof different size of electrically conductive beads on the uniformity of electric field distribution（n=3）

从图5中可见：在转筒中放入适当导电粒子可以提高微波腔内电场分布的均匀性，粒径越大，其对电场分布的改善越明显；在转筒未运动时，产生的导电粒子集中于转筒的某个位置，转筒内的电场分布极不均匀，随着转筒的转动，导电粒子在转筒中的分布呈随机分布状态，随机分布越均匀，电场分布也越均匀.在实际应用中，放置导电粒子的转筒在转动一定时间后再开启微波源，即可避免由于导电粒子在最初放置时较集中导致的电场不均匀现象.

导电粒子粒径对平均电场强度的影响见图 6.在400，s时平均电场强度均突然增大，其中粒径 d= 20，mm时的平均电场强度达到没有导电粒子时的1.4倍.主要原因是，此时 3个导电粒子分布比较集中（见图3），导致局部电场强度增大.

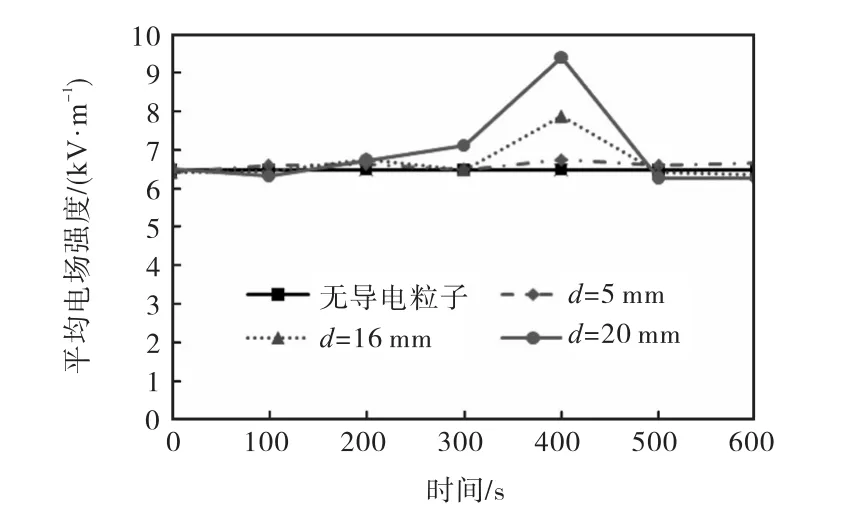
图6 导电粒子粒径对平均电场强度的影响（n=3）Fig. 6 Effect of different size of electrically conductive beads on average electric field intensity（n=3）

3.2 导电粒子数量对微波转筒腔内电场分布的影响

为了研究导电粒子数量对电场分布的影响，分别取对电场分布影响不明显的粒径（d=16，mm）和对电场分布影响较明显的粒径（d=20，mm）进行分析.

由图 7（a）和图 8（a）可见，当导电粒子直径 d= 16，mm时，导电粒子数量对电场分布和平均电场强度的影响很小，说明导电粒子尺寸对电场分布的影响起主要作用，当粒径影响较小时，通过增加粒子数量并不能改善电场分布的均匀性.

由图 7（b）和图 8（b）可见，当导电粒子直径 d= 20，mm时，随着粒子数量的增多，电场分布的均匀性下降，当粒子数n=7时，电场分布极不均匀，平均电场强度在200，s时急剧增大.其主要原因是当粒子数增大时，粒子在随机运动过程中，粒子之间的距离会减小，当金属粒子间距离小于一定值时，电场会在局部过度集聚，从而造成局部电场强度过大及电场分布均匀性的下降.在研究中，当n=7时，局部最大电场强度值达到 7.6×105，V/m，超过电场发生电离允许的最大值 1×105，V/m［25］，该种现象是在微波加热中必须避免的.

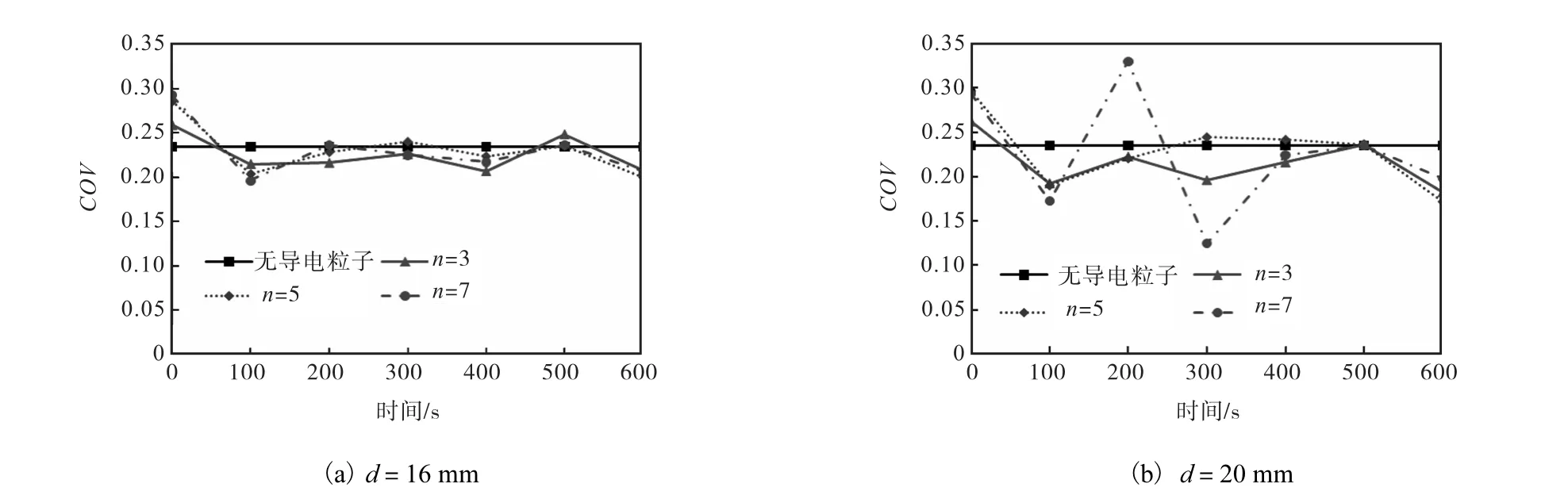
图7 导电粒子数量对电场分布的影响Fig. 7 Effect of different number of electrically conductive beads on electric field distribution

图8 导电粒子数量对平均电场强度的影响Fig. 8 Effect of number of electrically conductive beads on average electric field intensity

3.3 固定间距的导电粒子对微波转筒腔内电场分布的影响

尽管一定数量和尺寸的随机运动导电粒子可以提高微波腔内电场分布的均匀性，但自由随机运动的导电粒子会因运动中粒子集聚而导致局部电场强度过大，以至于超过电离允许的最大值.为了解决这一问题，本文在保证粒子间安全距离的前提下固定粒子间距，如图9所示，取3个直径为20，mm的导电粒子，其中粒子 1与粒子 2和 3表面间的距离为25，mm，粒子2和3表面之间的距离为20，mm，当转筒转动时，粒子随着转筒转动并沿着转筒的轴向方向随机运动.当保证粒子之间的安全距离后，粒子随着转筒沿着转筒轴向方向随机运动时，微波转筒腔内的电场分布均匀性相对没有导电粒子时提高了 39.87%（图 10（a））；同时，微波腔内的平均电场强度在 600，s内平均提高 18%左右（图 10（b）），这对于提高腔内的加热效率有着很好的作用.

图9 固定间距的导电粒子位置（n=3，d=20，mm）Fig. 9 The positions of fixed distance of electrically conductive beads（n=3，d=20，mm）

图10 不同随机运动导电粒子对电场分布和平均电场强度的影响（d=20，mm）Fig. 10 Effect of different random motion of electrically conductive beads on electric field distribution and average electric field intensity （d=20，mm）

4 结 论

本文仿真研究了随机运动导电粒子对微波转筒干燥腔内电场强度及电场分布均匀性的影响.研究发现，随机运动导电粒子可以改善微波腔内电场分布的均匀性，但导电粒子对电场分布的影响与其尺寸和数量有关.当粒径小于20，mm时，导电粒子对电场分布的影响较小.在粒径影响较大的情况下，随着导电粒子数量的增多，微波腔内电场强度因导电粒子间距离太小而造成过度集聚，严重者超过避免电离允许的最大值.固定导电粒子间隔后，在导电粒子随着转筒转动并沿着转筒轴向方向随机运动时，微波转筒腔内的电场强度得到明显提高，电场分布的均匀性提高39.87%，这对于提高加热效率及加热的均匀性有着重要的作用.

［1］ Datta A K，Anantheswaran R C. Handbook of Microwave Technology for Food Application［M］. New York：Marcel Dekker，2001.

［2］ Bogdal D. Microwave-assisted Organic Synthesis：One Hundred Reaction Procedures［M］. Oxford：Elsevier Science，2005.

［3］ Committee on Microwave Processing of Materials. Microwave Processing of Materials ［R］. Washington D C：National Academy Press，1994.

［4］ Katz J D. Microwave sintering of ceramics［J］. Annual Review of Materials Science，1992，22（1）：53-170.

［5］ Appleton T J，Colder R I，Kingman S W，et al. Microwave technology for energy-efficient processing of waste［J］. Applied Energy，2005，81（1）：85-113.

［6］ Blaszczak W，Gralik J，Klockiewicz-kaminska E，et al. Effect of γ-radiation and microwave heating on endosperm microstructure in relation to some technological properties of wheat grain［J］. Nahrung/Food，2002，46（2）：122-129.

［7］ Krokida M K，Maroulis Z B，Saravacos G D. The effect of the method of drying on the color of dehydrated products［J］. International Journal of Food Science & Technology，2001，36（1）：53-59.

［8］ Aleixo J A G，Swaminathan B，Jamesen K S，et al. Destruction of pathogenic bacteria in turkeys roasted in microwave ovens［J］. Journal of Food Science，1985，50（4）：873-875.

［9］ Rosenberg U，Bogl W. Microwave pasteurization，sterilization，blanching，and pest control in the food industry［J］. Food Technology，1987，41（6）：92-97.

［10］ Vadivambal R，Jayas D S. Non-uniform temperature distribution during microwave heating of food materials：A review［J］. Food and Bioprocess Technology，2010，3（2）：161-171.

［11］ Li Z Y，Wang R F，Kudra T. Uniformity issue in microwave drying［J］. Drying Technology，2011，29（6）：652-660.

［12］ George J，Bergman R. Selective re-meshing：A new approach to include mode stirring effects in the steady state FDTD simulation of microwave heating cavities［J］. Microwave and Optical Technology Letters，2006，48（6）：1179-1182.

［13］ Plaza-Gonzalez P，Monzo-Cabrera J，Catala-Civera J M，et al. Effect of mode-stirrer configurations on dielectric heating performance in multimode microwave applicators［J］. IEEE Transactions on Microwave Theory and Techniques，2005，53（5）：1699-1706.

［14］ Sebera V，Nasswettrová A，Nikl K. Finite element analysis of mode stirrer impact on electric field uniformity in a microwave application［J］. Drying Technology，2012，30（13）：1388-1396.

［15］ Bows J R. Variable frequency microwave heating of food［J］. Journal of Microwave Power and Electromagnetic Energy，1999，34（4）：227-238.

［16］ Wang Y C，Zhang M，Mujumdar A S. Study of drying uniformity in pulsed spouted microwave-vacuum drying of stem lettuce slices with regard to product quality［J］. Drying Technology，2013，31（1）：91-101.

［17］ Yang H W，Gunasekaran S. Comparison of temperature distribution in model food cylinders based on Maxwell's equations and Lambert's law during pulsed microwave heating［J］. Journal of Food Engineering，2004，64（4）：445-453.

［18］ Dominguez-Tortajada E，Plaza-Gonzalez P，Diaz-Morcillo A，et al. Optimisation of electric field uniformity in microwave heating systems by means of multifeeding and genetic algorithms［J］. Materials and Product Technology，2007，29（1）：149-162.

［19］ Wang S M，Hu Z C，Han Y B. Effects of magnetron arrangement and power combination of microwave on drying uniformity of carrot［J］. Drying Technology，2013，31（11）：1206-1211.

［20］ Ho Y C，Yam K L. Effect of metal shielding on microwave heating uniformity of a cylindrical food model［J］. Journal of Food Processing and Preservation，1992，16（5）：337-359.

［21］ Itaya Y，Uchiyama S，Hatano S. Effect of scattering by fluidization of electrically conductive beads on electrical field intensity profile in microwave dryers［J］. Drying Technology，2005，23（1/2）：273-287.

［22］ Wang R F，Huo H H，Dou R B，et al. Effect of the inside placement of electrically conductive beads on electric field uniformity in a microwave applicator［J/OL］. Drying Technology［2014-07-30］. http：// www. tandfonline. com/doi/abs/10. 1080/07373937. 2014. 929585.

［23］ Rattanadecho P，Cha-um W. Theoretical analysis of microwave heating of dielectric materials filled a rectangular wave guide with various resonator distances［J］. Journal of Heat Transfer，2011，133（3）：031008-1-031008-9.

［24］ 王瑞芳，李占勇，窦如彪，等. 水平转筒内大豆颗粒随机运动与混合特性模拟［J］. 农业机械学报，2013，44（6）：93-99.

［25］ 李占勇，Kudra T，王瑞芳. 微波干燥：机遇和挑战［J/OL］. 中国科技论文在线精品论文，2014，7（7）：683-688［2014-07-30］. http：//highlights.paper.edu.cn/ page_detail. php？id=2875.

随机运动导电粒子对微波腔内电场分布的影响

王瑞芳，王 喆，徐 庆，李占勇

Effects of Random Motion Electrically Conductive Beads on the Electric Field Distribution in Microwave Applicator

WANG Ruifang，WANG Zhe，XU Qing，LI Zhanyong
（College of Mechanical Engineering，Tianjin University of Science & Technology，Tianjin 300222，China）

Non-uniform heating is a major problem in microwave applications，mainly due to inherently uneven distribution of electromagnetic energy in the microwave applicator. This research work is aimed to improve the uniformity of electric field distribution by utilizing the microwave reflection of the electrically conductive beads which move randomly in a microwave rotary drum. Commercial softwares，EDEM and COMSOL，were coupled to simulate the interactions of multiphysical fields of the particles' movement and the electromagnetic field. The effects of size，number and ways of random movement of the electrically conductive beads on the electric field distribution in the microwave applicator were discussed. The results show that the influence of beads on the electric field is small when the bead diameter is less than 20，mm；beads in free random motion deteriorate the electric field distribution due to the agglomeration of beads；beads in random motion but restricted between a fixed distance can improve the intensity of the electric field and the uniformity of electric field distribution.

microwave heating；uniformity；rotary movement；electrically conductive beads；electric field

TQ051.5 文献标志码：A 文章编号：1672-6510（2015）02-0051-06

10.13364/j.issn.1672-6510.20140110

2014-07-30；

2014-10-10

国家自然科学基金资助项目（21106104）；高等学校博士学科点专项科研基金资助项目（20111208110004）

王瑞芳（1974—），女，内蒙古人，副教授，wangruifang@tust.edu.cn.

常涛