基于探地雷达的粮仓探测技术研究

于素萍，毛伟伟*,秦 瑶

(1.洛阳理工学院 计算机与信息工程系，河南 洛阳 471000；2.河南工业大学 信息科学与工程学院，河南 郑州450001)

0 引言

雷达电磁波具有穿透性强、探测便捷、维护方便等诸多优势，因此，利用探地雷达进行粮仓探测成为近几年粮食监管领域中的一个重点研究方向，利用探仓雷达可进行仓内异物成像[1]、异常层识别[2]、储量估算以及粮食湿度分布[3-4]等研究.本文首先分析了探地雷达的基本工作原理，然后针对粮仓的特殊应用环境，从雷达探测品质因子出发，根据粮仓仓底散射截面特性，结合粮食介质的衰减因子，推导出雷达最大探测深度计算公式，并对影响探测深度的因素进行了仿真分析.

1 探仓雷达工作原理

探仓雷达就是利用探地雷达技术进行粮仓探测，其基本探测原理与探地雷达[5]相同，见图1.雷达在粮面通过发射天线T发射一定频段的电磁波，遇到存在电性差异的界面时，电磁波就会产生反射信号，反射信号返回到粮面后被接收天线R接收，根据电磁波信号的双程传播时间△t，仓内实际储粮高度Z可由式(1)计算，

(1)

针对雷达回波中有异常反射的情况，也可根据反射信号的走时、强度等信息进行异物位置、性质等参数的判定，以解决粮堆仓储中，粮面以下异常目标的无损探测问题.

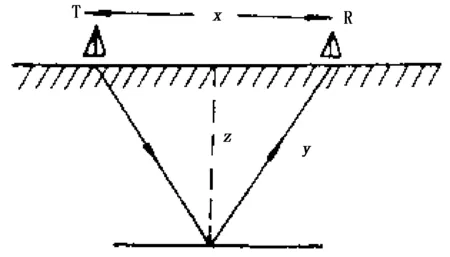
图1 反射探测原理Fig.1 Reflection detection principle

2 探仓雷达性能参数分析

不同仓型的粮仓，储粮高度有所不同.平房仓较浅，储粮高度在5～10 m；浅圆仓居中，在10～20 m；圆筒仓较高，储粮高度为30～60 m.无载频脉冲探仓雷达的探测距离和分辨率与待测媒质特性密切相关，粮食属于有耗媒质，对电磁波具有低通滤波效应，使得雷达的探测深度和分辨率互相矛盾.因此，探仓雷达的参数选择应当在二者之间折中考虑，即要满足探测距离的要求，又要保证足够的分辨能力[6].

2.1 探仓深度计算公式推导

电磁波的探测距离依赖于雷达波传播时媒质的电性属性、目标体的尺寸大小及目标体与周围介质的电性差异程度等因素，可由品质因子出发进行定性讨论.品质因子(Q)的定义为：接收天线能够接收到的最小回波信号功率与发射机馈入发射天线的功率比值[7]，即：

(2)

式2中：ξT为发射天线效率，ξR为接收天线效率，GT为发射天线方向增益，GR为接收天线方向增益，v为电磁波在粮食层中的传播速度，g为目标体的反向散射增益，ζ为目标体的散射截面积，α为地下介质的衰减系数，L为发射天线至目标体间的距离，f为天线中心频率.

粮食介质的衰减因子用α表示，则：

a=20lgeα=8.68α(dB/m).

(3)

将式(3)代入式(2)，式(2)可改写成式(4)，

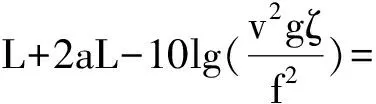
(4)

式(4)反映了探测深度与仪器性能参数、目标体及地下介质的关系.可以看出，雷达的探测距离涉及很多因素，一方面是由雷达体制决定，如发射源功率、天线的增益、覆盖的频率范围等；另一方面是由探测介质所决定，如媒质的介电常数、目标散射截面积、目标散射增益等因素.

对于粮仓储量探测，需要从雷达的探测结果中提取仓内粮堆的真实厚度信息，因此，式(4)中反射目标体为粮食层与仓底的交界面.粮仓的仓底一般为粗糙水泥面，根据工作经验，可近似地认为此类目标体的散射截面积接近第一菲涅尔带的面积，由图2可知，探仓雷达反射回波路径长度的最大值为：

(5)

其中，λ为电磁波在粮食中传播时的波长.目标体的散射截面积为：

(6)

当满足L≫λ时，ζ可写为：

ζ=πλL/2.

(7)

由于反射能量依赖于反射体表面的反射率，因此，gζ项为：

gζ=ρπλL/2，

(8)

其中，ρ为反射面的功率反射系数.

图2 粗糙界面散射截面积模型Fig.2 Rough interface scattering sectional area of the model

利用文献[10]所假设的gζ项关系模型：

gζ=10B1LB2fB3

(9)

其中:B1=lgπvρ/2,B2=1,B3=-1.

将式(9)代入式(4)得到雷达最大探测深度L的计算公式：

lgL+D1·L=D2.

(10)

式(10)中：

(11)

D1主要与地下介质电性参数相关，D2主要与雷达系统参数相关.

2.2 探仓深度影响因素仿真分析

为了更直观地了解上述影响因素对探测深度的影响，设探仓雷达收发天线的增益GT=GR=3 dB，收发天线耦合效率ξT=ξR=1/3，反射面的功率反射系数ρ=1/3.取粮食的介电常数实部为4，衰减系数为6 dB/m.将上述参数代入式(11)中，得到不同品质因子时，探测频率与探测深度的关系曲线如图3所示.可以看出，当雷达系统的品质因子一定时，探测深度随探测频率的增大而减小；当探测频率一定时，有效探测深度随系统品质因子的增大而增大.

本文的探测主要针对我国储粮的主力仓型平房仓和浅圆仓进行，根据这两种仓型的常见高度，确定最小探测距离应大于20 m.由图3可以看出，如果发射频率选为0.5 GHz，则要求探仓雷达系统的品质因子不小于110 dB；如果发射频率选为0.1 GHz，则要求系统的品质因子不小于90 dB.

图3 探测频率与探测深度的关系曲线Fig.3 Curve detection frequency and depth of investigation

3 实验

探仓实验在中储粮直属库-涿州粮库中储有小麦的浅圆仓进行.仓内实际储量高度为13 m.此雷达系统品质因子为90 dB；收发天线的增益约为3 dB；天线耦合效率约为1/3；反射面的功率反射系数约为1/3；仓内小麦电磁参数同2.2节，即介电常数实部为4，衰减系数为6 dB/m.由图3知：天线频率为0.1 GHz时，最大探测深度约为20 m；天线频率为0.3 GHz时，最大探测深度约为17 m；天线频率为0.5 GHz时，最大探测深度约为13 m.

结合实际仓内储粮高度，既要保证足够的探测深度，又要有尽可能高的探测精度，因此实验选用0.3 GHz杆状雷达天线进行测量.测量过程沿仓内直径方向进行探测，仓内长度方向为25.8 m，测量步长为3.5 cm，共测量737道数据.图4即为实测雷达图像.可以看出，在探测深度13 m处有持续稳定的明显反射，可判断13 m处为仓底的位置，与实际吻合.此外，观察图4，能较清晰地判断仓顶反射和异常目标体的反射(如图中圆形区域所示).实验结果证实了依据本文的计算方法选取合适的雷达系统和发射频率，能够准确地实现储粮深度探测，同时还能够进行仓内异常目标体的定位，为后续有效目标回波的提取提供了技术支持.

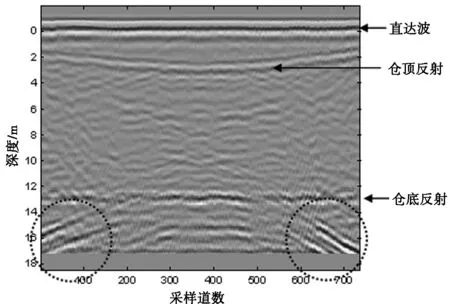
图4 探仓雷达实测图像Fig.4 Radar detecting image of barn

4 结论

本文结合粮食特性和粮仓特点，对探仓雷达最大探测深度的计算进行了详细推导，并进行了仿真．在实际探仓过程中，综合考虑粮仓仓形、实际储量高度、粮食的电磁特性、反射面以及天线参数等因素，选取合适的雷达系统和探测频率，能得到最优的探测性能.