粒子的散射方程、孤子解和高能统计模型

2015-08-08张一方张国玺

信阳师范学院学报（自然科学版） 2015年1期

张一方，张国玺

(1.云南大学物理系，云南昆明 650091; 2.郑州幼儿师范高等专科学校，河南郑州 450000)

0 引言

对于粒子的运动态主要研究弹性、非弹性及各种相互作用时的碰撞及多重产生.因此,各种粒子的碰撞截面在粒子物理中是一个十分具体的实验结果，并且积累了海量的实验数据.然而，从1980年到2010年,其中大部分结果都基本相同[1-2],但是对这些实验数据及图形的解释却是非常困难的问题，也是许多高深理论并不讨论的问题.

散射时只有基态强子及轻子、光子的散射，而共振态寿命太短，无法散射.散射实验结果主要有：1)非弹性散射部分所占比例不变，约为3/4.2)总截面上升[2].3)交叉对称性等.按能量散射可以分为低、中、高、超高能区域.超高能时联系于喷、多重产生.低能弹性散射对应Compton散射等.对pp弹性散射，低能时是库仑散射，高能时是Van der Waals(VdW)公式.

散射理论一般基于场论等纯理论，如WKB法、分波法、Born近似法等[3]，但通常无精确解.分波法是普遍方法，r→∞时相互作用可以略去，V(r)→0，最后结果与势无关，如此波函数、截面与粒子无关.量子力学的散射理论中有一个著名公式[3]，

(1)

而且散射截面σ(θ)=|f(θ)|2=|ψ2|2r2.分波法和Born近似法分别适用于低能和高能，如此中能散射应该在二者之间内插.量子场论中严格的散射理论，是基于散射矩阵和微扰论.散射中无限远时(入射前或后)是自由场方程，而散射时是相互作用场方程.此外也有一些散射的半唯象理论，如VdW公式及其推广，对总截面的Lipkin绘标.这又涉及标度性和部分子-夸克模型等.量子力学的方法是把相互作用归为势.碰撞时的方程应该是解相互作用耦合方程，然后相互作用化为流、势等.量子场论的散射矩阵理论拒绝讨论任何局域可观察量.散射矩阵满足数条公理：对称性，幺正性(这就是量子力学中的几率守恒)和解析性(对某些简单的散射过程，解析性是相对论因果律的推论).而粒子物理中存在各种对称性[1,4-5].

笔者在回顾粒子碰撞中的模型后，讨论了由这些碰撞得到的某些实验现象.并重点探讨了某几类碰撞截面和相应的散射方程.这些方程及截面是互相联系的，甚至是可以统一的.把方程归为四类：特殊函数方程、VdW方程、Γ分布及一般分布的方程和某些新的方程[6].散射总截面的变化可以认为是低能波动性(离散分布)越来越弱，最后趋于粒子性(连续、Γ分布).1990年基于统计性试图解释pp弹性散射截面[7].已知统计物理又类似量子场论[8].无相互作用则各种散射统一.R(p)方程的解是Bessel函数.相互作用作为微扰，则类似Born近似法.本文基于散射的实验结果，讨论散射的各种方程及相应的模型.

1 散射方程及其解

散射方程可以是量子场论方程，有势的量子力学方程，KdV方程等.

各种粒子相应的方程具有相同性和不同性.最基础的应该归为相互作用、拉氏量方程不同.如电磁相互作用不同的π+p,π-p；量子数S、I不同的Kp,πp等等.但结果必然还是与能量有关.对Kp,πp等，动力学模型的矢量场必须先化为标量场.理论上如果都化为夸克-胶子相互作用，则全部强相互作用碰撞应该统一.散射有n级近似就是存在n种相互作用，可以化为各种势，如反比曲线对应于基本相互作用，而波形图对应强相互作用等.

正正荷电pp、π+p等碰撞，可以是波形和Γ形的中插，最简单是二者结合.如联系于相对论立方方程，对应Higgs方程.低能时是非相对论立方Schrodinger方程，碰撞时是波形图，高能时对应于Higgs方程，孤子解又是Γ形图.

量子力学和量子场论方法结合则[9]：

σ∝d∑fi∝dWfi∝|Mfi|2∝|Sfi|2∝|ψ|2;

σ∝|T|2,τ-1∝|Tba|2.

(2)

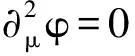
把各种截面都化为方程，有结果.

1)一般σ=C(ln (s/s0))α-1(s/s0)-β，所以

dσ/ds=(C/s0)(ln (s/s0))α-2(s/s0)-(β+1)

((α-1)-βln (s/s0)).

(3)

它包括多重数=A+Blns+C(lns)2及方程

d/ds=(B+2Clns)/s,

(α=2,β=0,s0=1).

(4)

α=1时包括Lipkin标绘dσT/ds=-Rs-3/2/2，Collins公式，火球模型，=a+blns或AEα等.β=0时包括夸克-部分子模型等的结果.

2)s0=1,β+1→b，(α-1)→a,则

dσ/dx=Cx-b(lnx)α(a-βlnx).

(5)

它包括量子电动力学(QED)中高能时的结果[10]：

a)对光子自由散射，

b)对e+e-→2γ，

dσ/dx=2π(α/m)2x-2(2-lnx).

c)光被库仑场散射，

dσ/dx=(3σ2/π2x-3(1-2lnx).

d)核场中单光子的对产生，

e)核场中单光子的相干散射，

f)对产生，dσ/dx=2Cx-3lnx(1-lnx).

但不包括双光子的标量介子对产生，

3)令lnx=y，则

dσ/dy=Ce-(b+1)yyα(a-βy).

(6)

进一步，一阶方程可以化为二阶方程，如式(6)化为

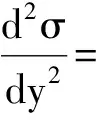
a(b+1)-β(α+1)).

(7)

如果C′e-(b+1)yyα=σ，则

(8)

C″e-(b+1)yyα-1=σ,

(9)

则

σ″=(βy2-my+γ)σ,

(10)

是谐振子势的Schrodinger方程

▽2ψ+2m(E-U0-(kx2/2)+akx-

(ka2/2))ψ=0.

(11)

解是

ψ=Cexp(-α2x2/2)H0(αx).

(12)

其能级是谐振子.

如果C‴e-(b+1)yyα+1=σ，则

σ″+(-β+(m/y)-(γ/y2))σ=0,

(13)

是库仑场中的Schrodinger方程

u″+(2m(E+Ze2/r)-l(l+1)/r2)u=0.

(14)

解是

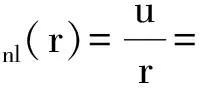
(15)

令r=lnx，则由此可解得QED散射中的某些高能截面：n=2,l=0是b)；n=2,l=1是c)；n=3,l=2或u21=rR21是e)和f).其中QED对应库仑场.

散射截面随能量改变，总截面有Lipkin绘标[13]：

(16)

非相对论ψ-φ方程的解是Laguerre函数[14]；而非相对论ψ-Aμ方程的解是Hermite函数[14].二函数在n=0,1时都是线性关系；n增大时就是多项式，对应波形图，能量越大，n越大.

对Laguerre方程

xy″+(1-x)y′+λy=0

(17)

的解是Laguerre函数L.λ=0，L=1对应PV/NkT=1；λ=1，L(C/V)=1-(C/V)是直线或反比式；λ=2,3,4等，L(C/V)更复杂.

对Pearson方程

(18)

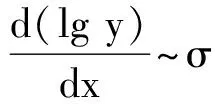
2 非线性方程的孤子解和碰撞解

笔者讨论过粒子物理中的各种非线性理论，如非线性波、非线性方程、复时空及其与几何、数学等的关系和可能的检验[15-16].具体描述粒子散射可以应用非线性方程的孤子解、碰撞解结合量子力学的散射截面得σ=A|ψ|2.弹性碰撞应该是孤子波碰撞解，而非弹性碰撞是耗散波或色散波的碰撞解.这必须首先发展数学方法.

对非线性Schrodinger方程的碰撞可以是：1)把相互作用作为势.2)发展为碰撞解.3)发展为非线性Dirac方程、Klein-Gordon(KG)方程等及其碰撞解.

研究具有非线性效应和色散效应，而不考虑耗散效应的浅水波等很大一类问题得到KdV方程[17].KdV方程计算结果或其平方类似某些散射截面.KdV方程的一般形式是：

(19)

其最简单的一种推广是：

φt+αφ2φx+φxxx=0.

(20)

目前主要都是研究一个方程的孤子碰撞解，这至多对应于相同粒子的碰撞.其中双子解应该等于碰撞解，对应于散射.发展为两个粒子的碰撞解，必须解孤子方程组.一般的方法是解一个方程再代入另一个.如果方程组化为非相对论的势方程，则是单个方程；其又可以化为非线性孤子方程.并且还必须考虑耗散效应及相应的结果.

进一步，应该发展一般的非线性Schrodinger方程(特例是立方Schrodinger方程)和非线性相对论Dirac方程、KG方程、Proca及Maxwell方程，其联系于非线性光学、激光等.并且研究它们的孤子解、碰撞解等.

初态或末态为n体的孤子碰撞在某一时刻或某一位置起码应该有n个峰，特别对两体相互作用.孤子用于两体弹性散射只能有两个峰，如π+p,K-p,pp的实验结果[1-2].

总截面对应于孤子解积分一次的Γ形孤子.这起码是一级近似，有起伏是高级近似.解碰撞粒子的方程组，这是严格解.在一定条件下化为一个方程，其必然是非线性方程.此时非线性项对应于势，非相对论时是非线性Schrodinger方程.

Γ形截面可以化为略有起伏的Γ形孤子解，再结合Λ(钟)形孤子解,即二者叠加.Γ形对x求导就是Λ形，反之是求积分.由此联系于Higgs方程，其解为Γ形、结合旋量场方程就可以进一步修改Γ形.冲击波和Burgers方程的解都是Γ形孤子.Γ形又类似Einstein-Debye固体理论的图形.其形式(起码一级近似时)是

(21)

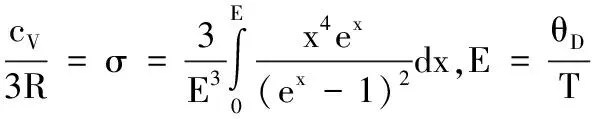
(22)

这是基于统计模型的碰撞理论.碰撞的相互作用势是谐振子势，热容量对应于截面.Γ形更类似原子核结合能曲线.这已有半唯象的公式和理论.

Γ形截面仅对总截面成立.强子碰撞，正正荷电者pp、pd、K+p、K+d、π+p总截面应该类似，高能时上升；K+p是Γ形孤子，上下截面各是12.7和 2.3[2].二阶方程是非线性Higgs方程，解为Ath(a+bx)，一阶方程是

(23)

这对应动力学模型及其Γ形孤子.

立方Schrodinger方程的解及其平方(即几率密度及截面)就导致Λ型孤子.方程对应于低速、低能，此时正好才有Λ型孤子.高能时都是平滑曲线，对应于统计性，应由高能时的方程导致，此时化为相对论量子力学方程，有非线性相互作用时就导致Λ型孤子或反比.一般是高低能叠加.这是解叠加.进一步应该是方程及相应的解统一.

基于量子力学非线性方程得到几率密度方程[14,18]：

dρ/dE=aρ(1-2ρ).

(24)

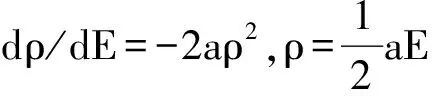
具体方法是：(A)解旋量场、标量场方程，然后平方得截面.(B)直接解密度及截面方程.费米子和玻色子方程形式上统一[14,19]，则

ψ″+cψ′+mψ+aψ″=0,

(25)

对应非线性振动方程，有极限环；又类似(统一的)立方Schrodinger方程，有Λ型孤子解.化为

pdp/dψ+cp+mψ+aψn=0,

(26)

原方程是变形的埃姆登方程

v″+(2u-1)v′+μ(μ-1)v+vn=0,

(27)

仅在特殊情况时解有限.

最好的方法是非线性Schrodinger方程、Dirac方程、KG方程或其他方程的解的叠加或Backlund变换等.碰撞作为方程解的叠加应该:1)同位旋空间的方程及相同的Feynman规则的粒子，如pp,pn及其反粒子等相同或相似;2)电磁相互作用，如pp是排斥力等，对应于电荷不同的库仑场.基础是几种力同时相互作用，即把截面σ分解为几种图形和相应的相互作用、解、方程的叠加.

3 共振态、弹性散射和非弹性散射

低能时散射常常得到共振态，高能时就是连续的非弹性区.π+p,π-p散射的总截面的波峰，在E—σ图中是△，N的部分共振态.而π-p的第一峰也是对应于△(1236)，不是N.如此σ(E)函数的极大值就是某些共振态的质量.总之，碰撞有时只产生共振态；有时还产生其他粒子.而对应波峰的粒子基本都是Regge共振态，除N(1520).Regge极上的重子基本都是波形峰.

共振态都是小质量、低自旋、窄宽度峰.共振态可以是:1)直接产生A+B→C+R，其中R→D+E+…;2)复合形成A+B→R→C+D+…，波形峰和Regge极都是如此.这类似复合核、中间态.散射曲线、动力学模型方程碰撞解的极大值就应导致Regge极S=aJ+b.二者统一为A+B→R+C(C≠0，或C=0).

散射可以化为复合中间态，类似复核，然后衰变.对碰撞复合粒子的中间态应用方程，费米子-费米子及玻色子-玻色子是KG方程，如γγ,NN；玻色子-费米子是Dirac方程，如γp(γd),π+p(N,d),Kp(N,d).引入中间态的总粒子是自由粒子方程，但有内部结构和相互作用.特别几率密度ρ∝ψ2方程就对应截面σ∝ψ2方程.这可以类比原子核、分子的碰撞.

对此首先分析实验数据[1-2]，同时进行分类.

1)弹性散射，有近似公式

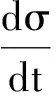
(28)

弹性散射在一定能量区域时主要是衍射.理论基础是热力学，统计性及量子液滴模型，其中

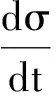
(29)

近似时化为Aeβt，再取近似就是直线式.对应于孤子碰撞解，孤波叠加.

2)非弹性散射，对应于统计性方程或特殊函数，及统计性的火球模型、激发态模型和部分子及其场论.这包括衍射.

进而研究弹性与非弹性散射的关系.推广研究总截面，结合Feld的渐近近似关系[20].弹性散射可以认为是纯粹的碰撞；非弹性散射则认为还必须有一个中间过程，如火球、激发态等.二者对应的粒子分别是稳定态和不稳定态.在极限碎裂模型(HLF)中，上一层粒子是非弹性散射，下一层夸克等是弹性散射.这可以结合标度假设.如果各类散射所占比例不变，则应由粒子内部结构决定.弹性散射占30%，这基本上也是胶子的比例.

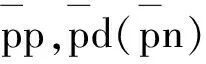
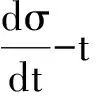
(30)

c<0和cb-a>0是反比曲线；c>0和cb-a<0是Γ型曲线；c>0和cb-a>0是上坡曲线；c<0和cb-a<0是L型曲线.积分得

(31)

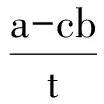
理论上，电磁、弱相互作用应该全部由QED、弱电统一理论决定.在QED中，截面常常在低能时是多项式，高能时散射截面几乎都有对数项，无论对轫致辐射或者对电离辐射[21].强相互作用电荷共轭C守恒，所以强子散射时Pomeranchuk定理[20]渐近成立，近似与电荷无关，符合很好.这说明高能时正负电荷的差别可以忽略.强相互作用中，p和n相同，pp与pn散射之间的差别是电磁相互作用.根据结构模型，截面之间可建立一定关系[20]：pp/pn=37.1/38.3，K+p/K+n=19.1/19.35都是电荷相同的截面较小，有一个中性粒子的截面较大.π+p/K+p=22.1/19.2，质量增大时截面变小.截面的总变化是：

K+p>K-n,π-p>π+p.

(32)

4 高能散射和统计模型

强子高能碰撞多重产生的许多模型，从预言次级粒子快度分布看，一是以多重边缘碰撞模型为代表，分布基本上在一个比较大的范围内均匀分布.二是以火球模型为代表，分布基本上集中在一个或几个小区域.

高能轻子(e,μ,v)与核子的散射说明大动量转移过程，即小距离处(<10-14cm)强相互作用变弱(渐近自由).高能粒子碰撞中多重数分布具有多分形结构[22].

量子力学一个最基本的特性就是统计性[8].这包括量子力学方程，非线性统计性的各种方程及其在高能时的解.高能时质量项可以略去，即无线性项，就是反比曲线.结合高能时统一方程[14]有

dψ/dη+mψ=J，其中m≈0.

(33)

无相互作用J=0时，σ=C是常数.有相互作用J≠0时，σ=J2(Ap+BE)2+C随能量、动量上升.进一步发展为非线性方程

dψ/dη+Aψn+1=0,ψ=(Anη+C)-1/n.

(34)

n=2时是Heisenberg统一方程[23].σ=|ψ|2=(1/2Aη)+C是反比关系.方程

ψ′+mψ+aψ″=0

(35)

相应的密度方程有Γ型孤子解.方程本身的解为

ψ=(Ce(n-1)mη-(a/m))-1/(n-1).

(36)

n=3时密度对应量子统计[14,24].对二阶方程

φ″±m2φ∓bφn=0,

(37)

可以有Λ型、Γ型孤子解；高能时对应波动方程应该是反比关系；m≈0，C=0时解为

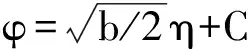
碰撞时的统计性只有两种：Fermi-Dirac(FD)或Bose-Einstein(BE)统计，其量子数不同，但不涉及具体的中间过程.粗略而言，可以分为同类粒子散射，对应气体状态方程；不同类粒子散射，对应自洽场方程.也可能不同方程对应不同能级，其实质是多体问题.自洽场方程近似时是托马斯-费米气体，其曲线类似Kendall分布.

统计性起码对散射成立，例如多重产生、各种统计模型、pp散射的VdW公式(这表明此时是热力学体系)等.散射可以是统计性结合特殊函数.但具体计算显示不可能是单独的任何函数.