浅谈数形结合在数学教学中的应用

闫子兰

[摘 要]数形结合，指在研究抽象的数的时候，借助具体直观的形帮助理解，即把抽象的知识具体形象化，从而达到事半功倍的效果。

[关键词]分析题意 概念本质 本质特征 数形结合 数学教学

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2015）21-039

数形结合的思维方法是理论与实际的有机联系，是思维的起点，是学生建构数学模型的基本方法。纵观整个小学数学教材，从一年级到六年级，无不体现数与形的有机结合。由于抽象思维与形象思维的结合，即数形结合，可以使学习内容变得比较易于理解，所以在课堂教学中，教师应帮助学生从直观到抽象，逐步建立起整个数学知识体系，培养学生的思维能力。那么，如何更好地引导学生以形象“解”抽象，是我们一线数学教师一直思考的问题。

一、利用数形结合，有助于学生分析题意

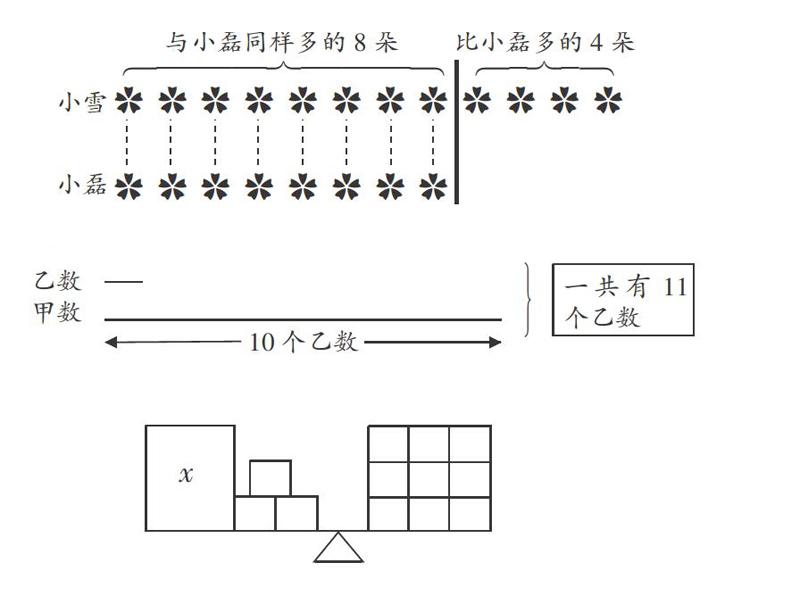
例如，在教学“小雪比小磊多几朵花”这个问题时，我让学生拿出学具，动手摆一摆并说说摆的过程。

师：小组讨论思考三个问题：（1）谁和谁比？（2）谁的多，谁的少？（3）多的分成几部分，是哪几部分？

根据直观的数与物（形）的对应关系，学生很快明白小雪的花分为两部分，一部分是与小磊同样多的花，另一部分则是小雪比小磊多的花，然后列出算式求解。

二、利用数形结合，有助于学生理解概念

小学生的数学认知结构主要是加法结构和乘法结构，而从加法结构到乘法结构，学生的认知结构需要发生一定程度上的“质”的变化。其中，“倍”的学习是认知结构发生“质”的变化的第一次机会，因此学生学习“倍”的知识感觉非常困难。我在教学时让学生在操作的基础上充分利用数形结合，建构倍的直观模型，以突破这个教学难点。通过感官操作，将图案与具体实物间建立一一对应的关系，使学生清楚地看到比较量有几个标准，就是标准量的几倍，从而由已有知识认识“倍”的数学概念。数形结合在这里体现的是数量与图形之间的对应关系，引导学生通过数与图的相互转化来明确两个比较量之间的数量关系，使他们很快就触及概念的本质。

三、利用数形结合，有助于学生理解量与量之间的抽象关系

我在平时的教学中很注重培养学生画线段图的能力，因为线段图能将抽象的数与数之间的关系具体形象地展现在学生面前，使他们轻松地理解题意。

例如，在数学五年级练习题中有这样一道题目：“甲数的小数点向左移动一位是乙数，甲乙两数的和是283.8。甲乙两数各是多少？”对于此题，大多数学生一看题目都感到无从下手。我引导学生发现甲乙两数存在着倍数关系——甲数是乙数的10倍，并提示用线段图来表示它们的关系。学生立刻正确的画出图（如下），直观地理解了题意，很快解答了问题。

四、利用数形结合，有助于学生理解知识的本质特征

在“简易方程”教学中，要求学生应用等式的性质来解方程。我在教学时充分利用天平让学生写等式，并多次变换天平两边的物体，引导他们明白等式的左边表示应做的运算，右边表示答案，等号表示左右两边的等价性，这为学生利用等式的性质解方程提供了强有力的支撑。

例如，在教学x+3=9时，教师出示图片（如右），并提问：“怎样让天平左边只剩下x？”

生1：从天平的左边拿走3个方框。

师：为了让天平仍然保持平衡，右边怎么办？

生2：从天平的右边也拿走3个方框。

师：用等式把这个过程表示出来。

生：x+3-3=9-3。

……

这样，通过数形结合，让学生明白方程的每一步都是一个等式。

华罗庚先生说过：“数与形，本是相倚依，焉能分作两边飞。数无形时少直觉，形少数时难入微。数形结合百般好，隔离分家万事非；切莫忘，几何代数统一体，永远联系，切莫分离！”这里明确指出了数形结合的价值，并揭示了数形结合的本质。也就是说，我们在研究抽象的“數”的时候，往往要借助于直观的“形”。数形结合既是一种重要的数学思想，也是一种智慧的数学方法。所以，教师在课堂中应将“以形助数”与“以数解形”有机地结合在一起，使教学收到事半功倍的效果。

（责编 蓝 天）