小学数学习题设计需注重三个方面

王琴

[摘 要]在小学数学教学中，习题设计是帮助学生巩固旧知，发展数学技能的有效途径。在进行习题设计时，应注重习题设计的针对性、综合性和思维性，运用有效的习题，训练学生的数学思维，提高学生的数学能力。

[关键词]习题设计 小学数学 针对性 综合性 思维性

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2015）20-054

习题设计在数学教学中的功效不言而喻，一方面可考查学生对知识的掌握情况，另一方面能培养学生对数学思想方法的灵活运用能力。在小学数学习题设计中，不论是化抽象为形象，还是化新知为旧知，教师习题设计的核心，都是要能够纲举目张、举一反三，促进学生的数学思考，发展学生的数学思维。现以“平均分”这一概念为例谈谈小学数学习题设计需注重的三个方面。

一、注重针对性，指向知识核心

习题设计的本质，是要能够强化学生所学知识，并将所学知识拿来熟练运用，突破学习的难点，解决数学问题。因而，教师要将习题设计的重心放在学生容易迷惑的地方，越是认知模糊，越是需要加强习题训练，由此突破数学难点，直指知识核心。

例如，在学生学完《分数的意义》之后，对“平均分”这个关键概念仍然没有建构深刻认知，还停留在浅层次上。为此，我设计了这样一道习题：一根绳子长5米，分成6段，每段绳长占几分之几？学生在做这道题时，认为绳子的长度除以6，就是每段绳子占总绳长的几分之几。结果整个班级几乎“全军覆没”。此时我让学生思考：想一想，题目中说将绳子分为6段，从这里你知道了什么？很快有学生反应过来，指出题目中的条件是“将绳子分为6段”，并没有标明平均分，因而这个题目给出的已知条件并不充分，也就没法进行解答。此时，我引导学生反思：你有什么教训？得到了什么启示？学生认为，自己忽略了“平均分”这个重要条件，由此从错误中获得深刻认知，明确了平均分在分数中所占据的重要地位。

二、注重综合性，沟通新旧知识

数学家华罗庚指出，读书的第一层境界是要将书读薄，将知识吸收拓展，内化成为自己的技能，书就可以扔掉了。对于习题设计来说，也应当如此。教师应将宏观和微观的教材都统合起来，沟通学生所学的新旧知识，将散落的知识由点到面，串成线、连成片，构建系统化的知识体系，将教材读薄读透，由此提升学生的数学思维。

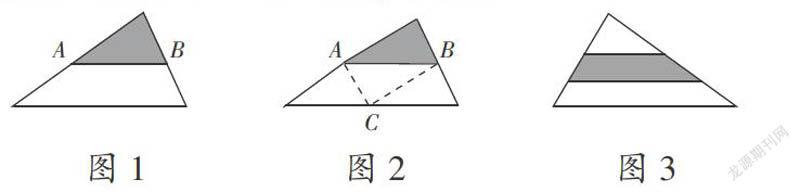
例如，在第一次习题设计中，学生对“平均分”这个字眼有了敏感度，那么，是否学生就对平均分有了深刻认知呢？我紧接着又设计了一道习题：如图1，A、B两点分别是三角形两条边的中线，阴影部分的面积占三角形面积的几分之几？（ ）。A.■ B.■ C.■ D.无法解答

学生认为，这里没有“平均分”的字眼，因而不能判断阴影部分面积占三角形的几分之几，此时我追问：再仔细读读题中条件，你发现了什么？学生经过仔细观察，发现隐藏着潜在的“平均分”：A、B两点是两条边的中线，假设C是底边的中点，那么可以再添加一条辅助线（如图2），这样就将三角形平分成了4等份，阴影部分的面积就是其中的一份，由此可以得到1/4。此时我继续引导：如果不用辅助线，运用我们学过的知识，怎么解答呢？学生认为，根据学过的“图形的放大和缩小”，大三角形是根据每条边2∶1的比例，将阴影部分放大，因而大三角形的面积是阴影部分三角形的4倍，由此可以得到阴影部分面积是大三角形面积的1/4。

以上习题设计，突破了数学习题中的表征形式，为学生学习后续的知识积累了经验，提升了学生的数学思维能力。

三、注重思维性，发展推理能力

教学中，常常有教师设计大量习题，目的是让学生提升技能，其实这种做法的最大误区在于，忽略了习题的思维性。练习的目的是为了提高思维能力，让学生从直观到抽象，逐步提升。

例如，针对“平均分”这个概念，学生如果只是掌握了内涵还远远不够，还需要教师设计相关练习，让学生深入其中，理解并体验它的外延。为此，我设计了第三道习题：如图3，将三角形的两条边分别三等分，阴影部分面积占原来三角形面积的（ ）。A.■ B.■ C.■ D.无法解答

学生基于上一道习题的经验，很快透过不平均的外表找到了隐藏在其中的“平均分”：三角形的两条边三等分，学生由此根据图形的放大和缩小的数学模型，展开演绎推理，将阴影面积和两个三角形面积建立联系，从而推算出阴影部分面积和整个大三角形面积的比为1/3。通过以上习题设计，学生不但获得了深刻的洞察力，而且大大提升了逻辑推理能力，发展了数学思维。

总之，在小学数学教学中，教师的习题设计不能盲目贪多，而是要精炼，具有针对性、综合性和思维性，这也是每道习题设计的精髓所在。

（责编 黄春香）