非平稳随机响应灵敏度分析的时域显式法

陈太聪，苏 成，胡智强，马海涛

(华南理工大学土木与交通学院，亚热带建筑科学国家重点实验室，广东 广州510640)

非平稳随机响应灵敏度分析的时域显式法

陈太聪，苏 成，胡智强，马海涛

(华南理工大学土木与交通学院，亚热带建筑科学国家重点实验室，广东 广州510640)

针对非平稳激励下的结构振动问题，研究动力响应方差灵敏度的高效时域求解算法。首先推导确定性动力响应灵敏度的时域显式表达，继而结合方差灵敏度的一般计算公式，得到非平稳随机响应方差灵敏度的时域显式计算列式。该列式同样适用于平稳激励下结构瞬态响应方差灵敏度的求解。以框架结构和桁架结构分别受不同类型的非平稳激励为例，时域显示解法和其他方法的对比计算结果验证了时域显示解法的有效性。

随机振动；非平稳；灵敏度；时域；显式法

引 言

灵敏度分析可以定量地确定系统参数的改变对系统响应的影响［1］，在结构优化、最优控制和系统辨识等领域有着广泛的应用。由于工程结构面对的大量激励如地震、风、海浪等作用属于随机过程激励，因此，开展针对随机振动响应的灵敏度分析具有重要的现实意义，相关研究日益受到关注。

根据随机过程激励的平稳性质不同，相应响应也可分为平稳随机响应和非平稳随机响应两类。其中，由于平稳随机响应较易求解［2］，相关灵敏度分析的研究较为成熟，已发展了包括有色噪声激励下的代数Riccati方程解法［3］、相关/非相关高斯激励下的模态分解解法［4］、高斯/非高斯激励下的响应多阶统计矩灵敏度计算的时域解法［5］、高斯激励下的虚拟激励解法［6］，以及随机结构情况下的Neumann展开结合Monte Carlo模拟解法［7］和虚拟激励结合点估计解法［8］等多种分析方法。

而对于第2类灵敏度问题，虽然地震、风、海浪等随机过程激励本质上都是非平稳的，相关分析更具现实意义，但由于非平稳随机响应的求解本身较为困难，因此相应的灵敏度分析还不易进行。近年来，Chaudhuri和Chakraborty［9］在频域内给出响应功率谱和各阶谱矩的灵敏度计算方法，进而得到响应方差和可靠度的灵敏度，其中需要进行双重频域积分；Cacciola等［10］结合动态模型修正和模态分解方法，建立了响应方差灵敏度的微分方程，采用递推法和逐步积分策略进行求解；Marano等［11］建立Lyapunov微分方程，求解响应方差的灵敏度，但仍限于单自由度系统的应用；徐文涛等［12］和刘齐茂［13］都从虚拟激励法出发，分别采用精细积分法和Newmark-β法推导了响应功率谱的一阶和二阶灵敏度的计算列式，前文继而给出了响应方差灵敏度的计算列式，需要说明的是，虚拟激励法的应用需要进行时域和频域内的混合积分计算。

近年来，苏成和徐瑞［14］提出了非平稳随机振动分析的时域显式法，通过建立的结构动力响应时域显式表达，可在时域内直接计算随机响应的均值和方差，还可以结合Monte Carlo模拟求解构件动力可靠度和体系动力可靠度［15］，在大型复杂结构中的应用显示了良好的计算效率［16］，在随机结构动力学问题［17］和 非线性随 机振动 问题［18］中也得 到 了应用，为非平稳随机响应灵敏度问题的研究打下了良好基础。本文将以该方法为基础，推导结构动力响应灵敏度的时域显式表达式，并以此进一步提出非平稳激励下随机响应灵敏度分析的时域显式法。最后通过数值算例说明本文方法的准确性和可行性。

1 动力响应分析的时域显式法

随机振动分析的时域显式法是基于结构动力响应的显式表达推导得到的［14］。以下就把该显式表达作一简要介绍。n自由度结构系统的运动方程可表示为

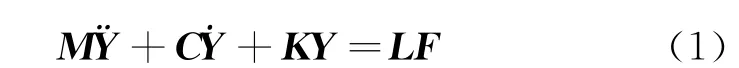
式中 K，C和M分别代表结构系统的刚度矩阵、阻尼矩阵和质量矩阵；Y，.Y和‥Y分别为位移向量、速度向量和加速度向量；L为一n×m阶激励影响矩阵；F为m维激励向量，若结构承受地震作用，则F为地面加速度。

式(1)可表示成状态方程的形式

若考虑线性结构系统，以及等时间步长Δt的计算，则一般地，第i时刻(ti=iΔt)的系统状态可递推地表示为

式中 矩阵Q0，Q1和Q2都依赖于结构参数和时间步长Δt。

若初始系统状态V0=0，则由递推式(4)可以推导得到第i时刻系统状态的时域显式表达为

则，显式表达式(5)可重新表示为

因此，所有时刻的系统状态可计算如下

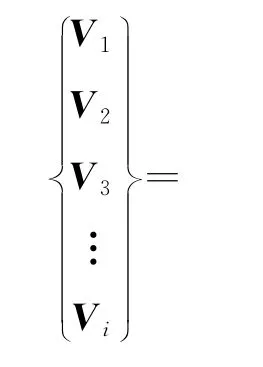
值得注意的是，系数Ai，j(0≤j≤i)的计算是一个递推过程，若采用精细积分法［19］进行求解，可得

由式(8)和(9)可见，为了得到各时刻系统状态对应的完整系数矩阵Ai，j，只需要计算系数矩阵的前两列Ai，0和Ai，1(i=1，2，…，l)即可，其计算量相当于两次确定性动力时程分析［14］。由式(6)可知，Bi也可以通过其前两列系数完全确定。

假设第i时刻关注的某个结构响应为vi，不失一般性，vi可由系统状态V和激励F计算得到

式中 φ为关注结构响应的定位行向量，其元素由0和1组成；S1和S2分别为系统状态和系统激励对结构响应的影响矩阵。根据所关注的结构响应的性质不同，S1和S2的具体取值也有所不同：①若关注结构响应为结点位移或速度，则S1=I，S2=0；②若为结点加速度，则S1=H，S2=W；③若为单元应力或应变，则在结点激励的情况下，S1可通过单元应力矩阵或应变矩阵计算得到，S2=0。

由式(7)和(13)，最终可得

2 动力响应灵敏度分析的时域显式表达

基于以上动力响应时域显式表达的基本思路，以下推导动力响应灵敏度的时域显式求解列式。

设θ代表结构的某个设计参数，在状态方程式(2)两端对θ求偏导，得

若激励F与参数θ无关，则式(15)可化简为

对比式(6)和(18)，再结合式(8)和(9)可知，要计算所有时刻点的系统状态灵敏度，只需要计算系数矩阵和的前两列，即可完全确定。

进一步地，结合式(13)和(17)可知，第i时刻关注结构响应vi对设计参数θ的灵敏度即可通过下式计算

3 随机动力响应灵敏度分析的时域显式法

由式(14)可知，当结构激励F为随机激励时，第i时刻结构响应vi的方差可表达为

将式(14)和(20)代入，最终整理可得第i时刻结构响应vi的方差对设计参数θ的灵敏度的计算表达式为

在实际工程结构中，较多关注结点位移或速度响应，此时，S1=I以及S2=0，则式(21)和(25)可分别化简为

在实际计算过程中，cov(Ri，Ri)的计算量和存储量可能过大，导致计算效率降低。为此，将式(31)右端的第二项展开，并整理后，得到以下更方便使用的计算表达式

需要说明的是，以上推导中并未对随机激励F的分布特性预设任何前提，因此，所得均方响应及其灵敏度的计算列式适用于各种类型的平稳/非平稳随机过程激励情况。对于平稳随机过程情形，通过本文列式获得的是全过程瞬态响应的方差及其灵敏度，相对于常规平稳随机振动分析得到的稳态阶段解答，信息更为丰富。

4 数值算例

采用FORTRAN语言实现了非平稳随机响应灵敏度分析的时域显式解法，并进行验证。本节给出两种结构的数值算例，分别与直接差分法、差分Monte Carlo模拟法和已有文献结果进行比较，说明本文方法的可靠性。

4.1 平面框架结构

采用图1所示平面4层框架结构模型，含20个梁单元，共36个自由度。所有单元的弹性模量E=3.0×1010N/m2，质量密度ρ=2.4×103kg/m3，梁、柱截面分别为0.25 m×0.40 m和0.35 m×0.35 m，考虑Rayleigh阻尼模型，阻尼矩阵由前两阶模态阻尼比(ξ=0.05)确定。

图1 平面框架结构模型Fig.1 Aplanar frame structure model

考虑非平稳限带白噪声激励，F(t)=g(t)x(t)，其中，均匀调制函数g(t)取为

其作用频带范围ω=0～200 rad/s。则该随机激励F(t)的相关函数可由下式计算得到

RFF(t+τ，τ)=g(t+τ)g(τ)Rxx(τ)

设计参数取为所有杆件的弹性模量E，计算总时长取为15 s，计算步长取Δt=0.005 s。

采用本文方法，计算结点 A的水平方向位移、速度和加速度的方差及其对设计参数的灵敏度随时间的变化规律，结果如图2～4所示。作为对比，图中还给出了采用直接差分法和差分Monte Carlo模拟法的计算结果。其中，直接差分法的计算过程是取设计参数的1‰变化量为差分步长，按式(21)分别计算设计参数变化前后的响应方差时程，进而用差分法计算灵敏度时程；差分Monte Carlo模拟法同样取设计参数的1‰变化量为差分步长，根据随机激励模型，人工生成一定数目的激励过程样本并进行动力时程分析，最后统计得到设计参数变化前后的响应方差时程，进而用差分法计算灵敏度时程。

图2 A点位移的方差及其灵敏度Fig.2 Covariance and its sensitivity of the node Adisplacement

实际计算中发现，由于Monte Carlo模拟得到的响应方差存在偏差，通过差分Monte Carlo模拟法计算得到的灵敏度值会发生偏差波动，但随着样本数增多，波动幅度会逐渐减小。在本例中，当样本数取为105时，灵敏度值波动幅度较小，因此，图中给出的Monte Carlo法结果均为105样本数的计算结果。

图3 A点速度的方差及其灵敏度Fig.3 Covariance and its sensitivity of the node Avelocity

图4 A点加速度的方差及其灵敏度Fig.4 Covariance and its sensitivity of the node Aacceleration

由图示结果可以观察得到：

(1)本文方法和直接差分法的结果基本一致，并都与差分Monte Carlo模拟法的结果趋势基本一致，验证了本文方法的正确性；

(2)方差的Monte Carlo模拟结果与理论计算结果的符合程度高于方差灵敏度，这是因为在差分步长变化前后，模拟得到的方差结果都存在一定的偏差，因此由差分计算得到的方差灵敏度的偏差会大于方差的偏差。由文献［1］的分析结果可知，响应灵敏度的差分模拟偏差会比响应的模拟偏差大1～2个量级，本算例与之相符。如前所述，计算中已验证，随着Monte Carlo样本数增加，方差的模拟偏差变小，方差灵敏度的模拟偏差也随之减小。

4.2 平面桁架结构

本算例取自文献［10］，采用的输电塔结构如图5所示。该结构有限元模型采用24个平面桁架单元，共20个自由度，所有单元具有相同的轴向刚度，EA=1.210 4×108N。考虑输电线的自重，结点9和12具有集中质量m=1 200 kg，其余结点具有集中质量m=600 kg。考虑Rayleigh阻尼模型，阻尼矩阵由前两阶模态阻尼比(ξ=0.02)确定。

考虑非平稳地震作用，采用均匀调制的平稳随机过程来模拟非平稳地面水平运动加速度‥x(t)，其中平稳随机过程采用以下Tajimi-Kanai功率谱

S0=0.05 m2/s3，ωg=4πrad/s，ζg=0.6均匀调制函数g(t)取为

则该随机激励的相关函数可由下式计算得到：

图5 平面桁架结构模型Fig.5 Aplanar truss structure model

设计参数取为所有杆件的轴向刚度EA，计算总时长取为15 s，计算步长取Δt=0.01 s。

图6 结点12位移的方差灵敏度时程Fig.6 Sensitivity of covariance of the node 12 displacement

采用本文方法，计算结点12的水平方向位移的方差对设计参数的灵敏度，结果如图6所示。由图示结果可见，本文方法与文献［10］中的灵敏度分析结果基本一致，进一步验证了本文方法的正确性。

5 结 论

本文基于动力响应分析的时域显式法，提出了非平稳随机响应灵敏度分析的时域显式法。利用灵敏度方程与状态方程的相似性，推出动力响应灵敏度的时域显式表达。继而利用时程方差灵敏度计算的一般公式，最终得到结构响应方差灵敏度分析的时域显式表达式。不同类型的算例计算结果验证了本文方法的正确性。本文的时域显式方法不要求随机过程激励具有特殊分布特性，因此，可以广泛适用于各种类型激励情况下的平稳/非平稳随机响应灵敏度分析。

［1］陈太聪，韩大建，苏成.参数灵敏度分析的神经网络方法及其工程应用［J］.计算力学学报，2004，21(6)：752—756.Chen Taicong，Han Dajian，Su Cheng.Neural network method in parameter sensitivity analysis and its application in engineering［J］.Chinese Journal of Computational Mechanics，2004，21(6)：752—756.

［2］Soong T T.Random Vibration of Mechanical and Structural Systems［M］.Englewood Cliffs：PTR Prentice Hall，1993：172—198.

［3］姚昌仁，麻永平.结构随机激励的响应灵敏度分析［J］.力学学报，1990，22(1)：438—445.Yao Changren，Ma Yongping.The response sensitivity analysis for structural systems in random excitation［J］.Acta Mechanica Sinica，1990，22(1)：438—445.

［4］Tong W H，Jiang J S，Gu S N.Dynamic design of structures under random excitation［J］.Computational Mechanics，1998，22(5)：388—394.

［5］Benfratello S，Caddemi S，Muscolino G.Gaussian and non-Gaussian stochastic sensitivity analysis of discrete structural system［J］.Computers and Structures，2000，78：425—434.

［6］徐文涛，张亚辉，林家浩.基于虚拟激励法的车辆振动灵敏度分析及优化［J］.机械强度，2010，32(3)：347—352.Wu Wentao，Zhang Yahui，Lin Jiahao.PEMbased sensitivity analysis for vehicle ride comfort and optimization［J］.Journal of Mechanical Strength，2010，32(3)：347—352.

［7］Bhattacharyya B，Chakraborty S.Stochastic dynamic sensitivity of uncertain structures subjected to random earthquake loading［J］.Journal of Sound and Vibration，2002，249(3)：543—556.

［8］乔红威，吕震宙.随机结构随机激励下的响应灵敏度分析［J］.振动与冲击，2008，27(3)：60—62.Qiao Hongwei，Lu Zhengzhou.Response sensitivity analysis of stochastic structures under non-stationary random excitation［J］.Journal of Vibration andShock，2008，27(3)：60—62.

［9］Chaudhuri A，Chakraborty S.Sensitivity evaluation in seismic reliability analysis of structures［J］.Computer Methods in Applied Mechanics and Engineering，2004，193(1/2)：59—68.

［10］Cacciola P，Colajanni P，Muscolino G.Amodal approach for the evaluation of the response sensitivity of structural systems subjected to non-stationary random Processes［J］.Computer Methods in Applied Mechanics and Engineering，2005，194：4 344—4 361.

［11］Marano G C，Trentadue F，Morrone E，et al.Sensitivity analysis of optimum stochastic nonstationary response spectra under uncertain soil parameters［J］.Soil Dynamics and Earthquake Engineering，2008，28：1 078—1 093.

［12］Xu W T，Zhang Y H，Lin J H，et al.Sensitivity analysis and optimization of vehicle-bridge systems based on combined PEM-PIMstrategy［J］.Computers and Structures，2011，89(3/4)：339—345.

［13］Liu Q M.Sensitivity and Hessian matrix analysis of power spectral density functions for uniformly modulated evolutionary random seismic responses［J］.Finite Elements in Analysis and Design，2012，48：1 370—1 375.

［14］苏成，徐瑞.非平稳激励下结构随机振动时域分析法［J］.工程力学，2010，27(12)：77—83.Su Cheng，Xu Rui.Random vibration analysis of structures subjected to non-stationary excitations by time domain method［J］.Engineering Mechanics，2010，27(12)：77—83.

［15］苏成，徐瑞.非平稳随机激励下结构体系动力可靠度时域解法［J］.力学学报，2010，42(3)：512—520.Su Cheng，Xu Rui.Time-domain method for dynamic reliability of structural systems subjected to non-stationary random excitations［J］.Chinese Journal of Theoretical and Applied Mechanics，2010，42(3)：512—520.

［16］苏成，徐瑞，刘小璐，等.大跨度空间结构抗震分析的非平稳随机振动时域显式法［J］.建筑结构学报，2011，32(11)：169—176.SU Cheng，XU Rui，LIU Xiaolu，et al.Non-stationary seismic analysis of large-span spatial structures by time-domain explicit method［J］.Journal of Building Structures，2011，32(11)：169—176.

［17］Su C，Xu R.Random vibration analysis of structures by a time-domain explicit formulation method［J］.Structural Engineering and Mechanics，2014，52(2).

［18］Su C，Huang H，Ma HT，et al.Efficient MCS for random vibration of hysteretic systems by an explicit iteration approach［J］.Earthquakes and Structures，2014，7(2)：119—139

［19］钟万勰.结构动力方程的精细时程积分法［J］.大连理工大学学报，1994，34(2)：131—136.Zhong Wanxie.On precise time-integration method for structural dynamics［J］.Journal of Dalian University of Technology，1994，34(2)：131—136.

An explicit time-domain method in sensitivity analysis of non-stationary random responses

CHEN Tai-cong，SU Cheng，HU Zhi-qiang，MAHai-tao
(State Key Laboratory of Subtropical Building Science，School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510640，China)

Aiming at the structural vibration problem under non-stationary excitation，time-domain method of high efficiency is explored in the present study to determine the sensitivity of covariance of random response.Firstly，a time-domain formulation is derived for computing the sensitivity of deterministic response.Then，according to a general expression of the sensitivity of covariance，an explicit time-domain formulation is deducted to calculate the sensitivity of covariance of non-stationary random response.This formulation is also suitable for the case of stationary excitation if sensitivity of covariance of the transient response is concerned.By taking a frame and a truss subjected to different types of non-stationary excitations as examples，comparisons of the numerical results obtained with different methods illustrate the effectiveness of the proposed method.

random vibration；non-stationary；sensitivity；time-domain；explicit method

O324；TU311.3

A

：1004-4523(2015)04-0503-07

10.16385/j.cnki.issn.1004-4523.2015.04.001

陈太聪(1977—)，男，副教授。电话：13903019936；E-mail：cvchentc@scut.edu.cn

苏成(1968—)，男，教授。电话：(020)87112755；E-mail：cvchsu@scut.edu.cn

2014-03-21；修订日期：2014-06-22

国家自然科学基金资助项目(51078150)；亚热带建筑科学国家重点实验室自主研究项目(2013ZA01，2015ZC19)；中央高校基本科研业务费资助项目(2013ZZ0024)和广西科学研究与技术开发计划资助项目(1298011-1)