灰色-权马尔可夫的地区航空货运量预测

潘开灵，尤佳滢，贾向南

（武汉科技大学 管理学院，湖北 武汉 430080）

灰色-权马尔可夫的地区航空货运量预测

潘开灵，尤佳滢，贾向南

（武汉科技大学 管理学院，湖北 武汉 430080）

建立了航空货运量的灰色-权马尔可夫预测模型，以灰色GM（1，1）对航空货运量进行预测，并根据历史数据的拟合结果划分出马尔可夫状态，再以权马尔可夫链进行短期状态预测，进一步修正灰色预测结果。实例结果显示，该模型较灰色GM（1，1）预测准确性更高，能反映出航空货运量的随机波动，适合于地区航空货运量的预测。

灰色预测；马尔可夫；航空货运量；预测

1 引言

航空运输系统是社会经济系统的子系统，不仅受到外部经济因素的影响，亦对经济社会起促进作用。影响航空运输的因素繁多，取决于经济发展水平、对外经贸联系程度以及旅游业的发展等众多条件，且受地区经济的影响明显[1]。表现在地区航空货运量上，呈现出明显的波动特征（如图1所示），进行预测时有显著的不确定性。但就全国范围的预测而言，航空货运量与国家整体经济运行有关，其时间序列表现出明显的趋势性，不确定性较小。

图1 武汉市航空货运量

目前，货运量的定量预测方法有时间序列分析法、回归预测法及灰色预测法等[2]。时间序列分析根据历史数据，以时间作为自变量进行预测，割裂了航空货运量与经济社会因素的内在作用；回归预测需要大量的历史数据，而地区航空货运量数据量较少且呈现出某种趋势性的非平稳序列，因此，回归预测多用于全国货运量的预测；影响航空货运量的因素其中很多满足灰色系统要求，且数据多为时间序列，只需收集较少的历史数据，就能预测出精度较高的短期数据，但由于灰色预测采用了累加生成列，对长期预测呈现一定的指数规律且对随机波动性较大的数据数列拟合结果较差。采用灰色-马尔可夫模型进行预测，虽然结合了灰色预测和马尔可夫预测的优点，但通常都只考虑了单步距的概率转移矩阵，忽视了前面若干年与预测期之间的相互关系[3-4]。

因此，本文以灰色预测对航空货运量进行短期预测，并针对地区航空货运量可能出现的波动状态，运用多步距的加权马尔可夫链对状态间的转移规律进行预测，对灰色预测结果做出修正。

2 灰色-权马尔可夫预测模型

2.1 灰色-权马尔可夫预测思路

灰色-权马尔可夫预测思路如图2所示。

图2 灰色-权马尔可夫预测思路

我国地区航空货运市场起步较晚，历史数据样本较少，加之其波动性较大、深受地区经济发展等多因素影响，使用数理统计方法建模预测比较困难。灰色GM（1，1）预测具有所需历史数据较少、计算简便、短期预测精度高等优点，不必考虑众多的复杂因素，从自身时间序列中寻找其内在规律，可以对地区航空货运量进行较为理想的初步预测。

灰色GM（1，1）预测对平稳序列进行有效拟合，而地区航空货运量是一个非平稳时间序列，存在较强的随机波动性。以灰色拟合精度（拟合值/原始数据）刻画其随机波动性，其结果具有非平稳随机过程的特征。因此，可以根据偏离程度划分出马尔可夫状态，结合马尔可夫链的无后效性特征，得出灰色拟合精度的波动规律，对预测期的马尔可夫状态做出判断。

文献[3]和[4]在灰色预测的基础上，对预测期的马尔可夫状态做出了预测。但其均采用单步距概率转移矩阵进行状态预测。地区航空货运量这一随机变量具有相依性[1]，仅使用单步距概率转移矩阵考察最近一年对预测期的影响缺乏严谨性。灰色拟合精度的各自阶相关系数能够描述各步距之间的相关关系及其强弱，因此，本文在进行预测期的状态预测时，考察多个年份对预测期的影响，将其马尔可夫概率转移矩阵作为权值，各步距的自相关系数的强弱关系作为权重，进行加权求和，以加权和的最大值所对应的状态为预测年份的权马尔可夫状态。

地区航空货运量的原始序列中，某个马尔可夫状态的残差平均值反映了该状态下灰色拟合值对原始数据的偏离情况。根据预测期马尔可夫状态所对应历史状态的残差平均值，就可以对预测期的GM（1，1）结果做出有效修正。

2.2 建立GM（1，1）模型，进行灰色预测[5]

考虑地区航空货运量的连续历史数据作为原始生成序列X(0)：

对X(0)进行一次累加生成变化（1-AGO）得X(1)：

上标“0”表示原始序列，上标“1”表示一次累加生成序列。其中：

令Z(1)为X(1)的紧邻值生成（MEAN）序列，那么:

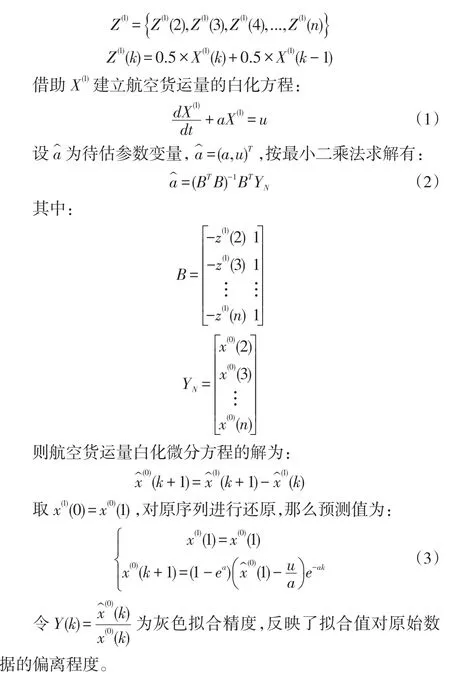
2.3 权马尔可夫预测的步骤

（1）马尔可夫状态的划分。各年航空货运量随时间变化呈增长趋势，且具有明显的随机波动性，不同年份的状态边界与内涵均是变化的。灰色拟合精度Y（k）反映了预测值和原始数据之间的动态变化，具有非平稳随机过程的特征。因此根据灰色拟合精度Y（k）划分出n个马尔可夫状态。

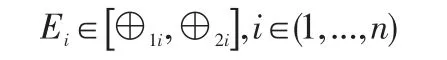
其中Ei为第i种状态⊕1i，⊕2i分别为第i种状态的上下界。

进行状态划分时，可以根据历史数据的多寡来决定状态数量。历史数据少时，用较少的状态数量来客观反映状态间的转移规律；历史数据多时，可以多划分些状态数目，以便挖掘出更多的信息，预测精度也会更准。状态划分的方法有样本均方差和聚类分析[6]，本文选择聚类分析中的K均值聚类进行状态划分。

（2）构建多步距转移概率矩阵。设由状态Ei经过步距m到达状态Ej的概率为 pijm。

mijm为状态Ei经过m步转移达到Ej的次数；Mi为状态Ei出现的次数。鉴于历史数据状态列变化趋势的不稳定，在计算步距为m的转移概率矩阵时，需要去掉数据序列中最末的m-1年。

则步距为m的转移概率矩阵为：

（3）计算各步距转移概率矩阵的自相关系数rk和权重Wk。为准确反映各步距（滞后期）转移矩阵对马尔可夫链预测的权重影响，用灰色拟合精度Y(k)的各阶自相关系数rm反映。

对各步距权值进行归一化处理，得各步距权重。

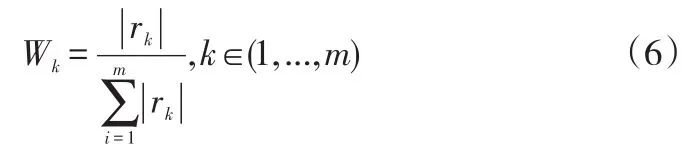
（4）预测期的马尔可夫状态预测，权马尔可夫链预测是对预测年份的马尔可夫状态做出预测。采用多步距的转移概率矩阵加权的方式进行。设某年灰预测精度指标的马尔可夫状态为Ei，距预测年份k年，转移概率矩阵为Pik，可以预测出该年份预测精度指标的状态转移概率向量。考虑距预测年份的步距为小于m的所有年份，即得预测年份马尔可夫状态的概率向量。

取max{Pi}所对应的状态为预测年份灰色拟合精度的权马尔可夫状态。

2.4 灰色预测结果的进一步修正

确定了预测年份的权马尔可夫状态Ei后，对灰色GM（1，1）预测结果做出进一步修正。

ii

取能见度为1 km，平流雾和辐射雾的谱分布如图1所示.由图1可知，当能见度为1 km时，随着粒子半径的增加，两种雾的谱分布曲线均先增加后减小，且两种雾的浓度在半径较小一侧迅速增大，在半径大的一侧则缓慢减小.其中平流雾的雾滴粒子半径较集中在2～5 μm，辐射雾的雾滴粒子半径较集中在0.1～2 μm，且辐射雾粒子浓度约大于平流雾粒子浓度两个数量级.

3 实例研究

本文以武汉市航空货运量为例进行预测。首先基于1995-2010年历史数据对2011年航空货运量进行预测，以灰色GM（1，1）拟合历史数据进行初步预测，然后用权马尔可夫对预测年份的状态进行预测，最后修正初步预测值，与实际观测值进行对照。对2012年和2013年用同样的方法进行递推预测。

3.1 武汉市航空货运量的灰色预测

根据2013年武汉市统计年鉴中1995-2011年航空货运量观测值，建立灰色GM（1，1）预测模型（见式（1）-（3）），使用matlab编程计算出1995-2011年航空货运量预测值（见表1）。依据预测值与观测值的比值及差求得1995-2010年的灰色拟合精度和各年度的残差值（见表1）。

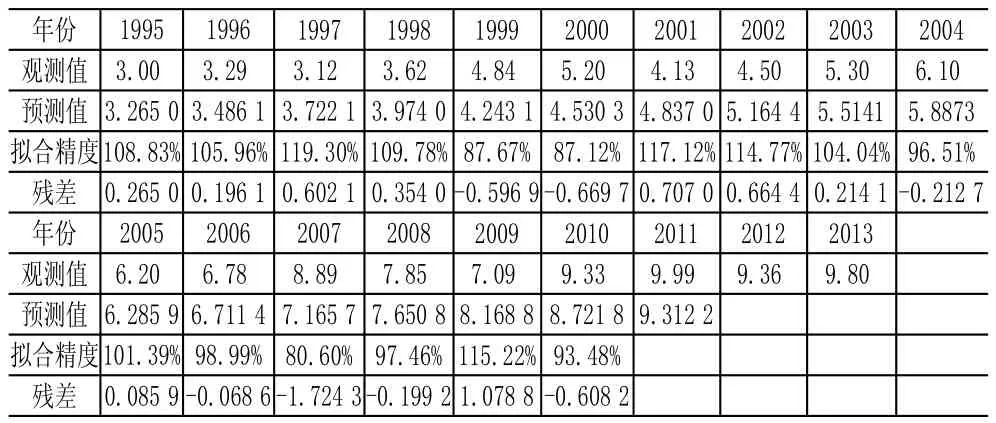
表1 武汉市1995-2013年航空货运量观测值及GM（1，1）预测值

注：数据来自《武汉市统计年鉴2013》。

从历史数据的拟合结果看出，由于武汉航空货运量的实际波动较大，需进一步使用权马尔可夫链对2011年的马尔可夫状态进行预测，在此基础上对预测结果做出修正。

3.2 武汉市航空货运量的权马尔可夫预测

3.2.1 马尔可夫状态的划分。对1995-2010年拟合精度指标使用K均值聚类方法，将拟合精度值均分化为四类，从而划分为四种马尔可夫状态，各预测期拟合精度的状态见表2。

表2 武汉市1995-2010年航空货运量预测期拟合精度的状态

（1）E1强高估年份，Y(k)＞109.30%，表示预测值远大于实际值，实际货运量可能出现了负增长或增长远低预期，该状态出现了4次。

（2）E2高估年份，100%＜Y(k)≤109.30%，表示航空货运量一定程度被低估，实际增长幅度低于预期，该状态出现了5次。

（3）E3低估年份，87.12%＜Y(k)≤100%，表示航空货运量一定程度被高估，实际增长高于预期，该状态出现了6次。

（4）E4强低估年份，Y(k)≤87.12%，表示预测值远小于实际值，实际货运量增长远超预期，该状态出现了1次。

3.2.2 多步距马尔可夫转移矩阵的获取。根据表2中航空货运量预测期拟合精度的状态，统计出1995-2010年依次年份顺序每个状态到另一状态的次数，依据式（4），计算一步矩阵P1时，统计得出状态1到1,2,3,4的状态次数分别为1,2,1,0次，由此得出矩阵第一行，依次类推出状态2,3,4分别到各状态的概率，最终得出一步矩阵P1。依次类推，得出P2，P3，P4，P5，需注意的是，多步矩阵的计算中，应统计跨m步的年份的各状态转换的对应值。

因此计算得出，步距为1，2，3，4，5的一步马尔可夫概率转移矩阵，分别为：

3.2.3 自相关系数及权重。根据表1中得出的精度拟合指标，结合式（5）和式（6）可以计算精度拟合指标的各阶自相关系数和权重（对于货运量序列，通常只考虑前5阶）。自相关系数为r1=0.152,r2=-0.428,r3=-0.091,r4=0.105,r5=-0.058，权重为 w1= 0.182 3，w2=0.513 2，w3=0.109 1，w4=0.125 9，w5=0.069 5。

3.2.4 航空货运量预测。根据以上概率转移矩阵和权重可以预测2011年的拟合精度状态。考察2006-2010年的拟合精度状态，分别为E3，E1，E3，E4，E3，确定对应的概率转移向量、步距和权重，由式（7）得表3。

表3 2011年拟合精度状态预测

因此，根据表3的数据显示2011年航空货运量的拟合精度最有可能处于E3。由灰色GM（1，1）计算的2011年预测值为9.312 2，训练样本中拟合精度为E3的平均残差 -δ3= -0.392 5，由式（8）得到2011年的航空货运量有可能为：

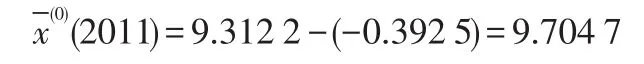
同理可以预测2012-2013年武汉市航空货运量，结果见表4。

3.3 两种方法预测结果的比较

将灰色GM（1，1）预测模型与灰色-权马尔可夫预测得到的2011-2013年结果进行比较，结果见表4。

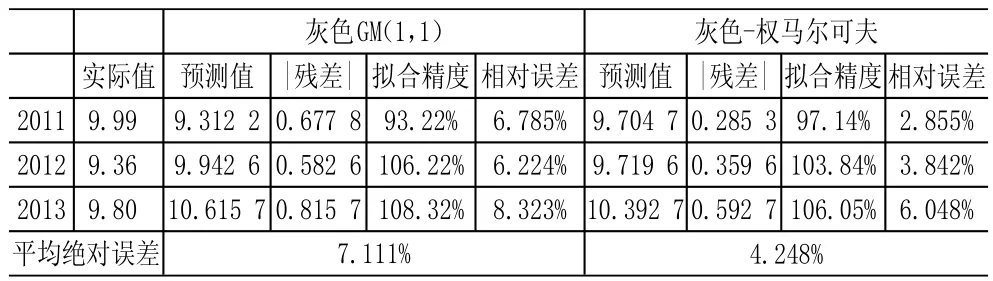
表4 两种方法预测结果比较

从表4两种预测方法结果比较中可以看出，灰色-权马尔可夫模型的各项预测误差均小于灰色预测，其主要原因是对各预测期的灰色拟合精度的权马尔可夫状态做出了预测，并根据历史状态的残差平均值对灰色预测结果做出了修正，较单独运用GM（1，1）模型精度有了进一步提高，说明该模型的预测结果是有效可靠的。

4 结论

影响航空货运量的因素非常多，较之全国性预测，地区航空货运量受地区经济影响更大，具有明显的趋势性，且随机波动性更强、历史数据更少。对于这类对象的预测，目前主流预测方法的预测精度都有待提高。灰色GM（1，1）预测对历史数据进行较好的拟合后再进行预测，但在对地区航空货运量这类随机波动性较强数据进行预测时，直接预测结果准确性不高。针对这一特点，本文结合灰色理论和马尔可夫预测方法，以灰色拟合精度划分马尔可夫状态，采用多步距状态转移概率矩阵加权求和的方式对预测期的马尔可夫状态做出了预测，并根据历史状态的残差平均值对灰色预测结果进行修正。实证分析结果表明：

灰色GM（1，1）预测与马尔可夫预测方法相结合，能充分利用历史数据给予的信息。在考虑多步距状态转移概率矩阵的基础上，加权求和来判断预测期马尔可夫状态可以更合理地捕捉地区航空货运量的随机波动性，提高了预测精度并增强了预测结果的可靠性，拟合和预测结果具有明显优势。此外，本预测方法不仅适用于地区航空货运量，稍加推理也可应用于其他具有明显趋势性和波动性对象的预测研究。

值得指出的是，在进行马尔可夫状态划分时，至少应划分出4个马尔可夫状态，以提高预测的准确性。同时也要注意应避免状态划分导致多步距状态转移概率矩阵中出现某状态概率过高的情况，影响预测期马尔可夫状态的判断。因此，如何更加合理的、科学的划分马尔可夫状态需要进一步研究。

[1]管驰明.50多年来中国空港布局演变及其影响因素—基于空间分析和数理统计的方法[J].经济地理,2008,28(3):445-449.

[2]陈实.货运量预测方法及应用研究[D].武汉:武汉理工大学,2008.

[3]文军.基于灰色马尔可夫链模型的航空货运量预测研究[J].武汉理工大学学报:交通科学与工程版,2010,34(4):695-698.

[4]盖春英,裴玉龙.公路货运量灰色模型-马尔可夫链预测方法研究[J].中国公路学报,2003,16(3):113-116.

[5]陈绵云.趋势关联度及其在灰色建模中的应用[J].华中理工大学学报,1994,22(8):66-68.

[6]赵欣,邹良超,倪林.基于有序聚类的模糊加权马尔可夫模型在降雨预测中的应用[J].江西农业学报,2009,21(2):110-113.

[7]邓聚龙.灰色预测与灰决策[M].武汉:华中科技大学出版社,2002.

[8]林小平,袁捷.基于灰色模型的成都双流机场物流预测[J].武汉理工大学学报:交通科学与工程版,2007,31(3):457-459.

[9]刘思峰,谢乃明.灰色系统理论及其应用[M].北京：科学出版社,2008.

[10]熊岗,陈章潮.灰色预测模型的缺陷及改进方法[J].系统工程,1992, 10(6):32-36.

Forecasting of Regional Airway Freight Transportation Volume Based on Grey Weighted Markov Model

Pan Kailing,You Jiaying,Jia Xiangnan
(School of Management,Wuhan University of Science&Technology,Wuhan 430080,China)

In this paper,we established the grey weighted Markov model to forecast the airway freight transportation volume:first we forecast the airway freight transportation volume using the GM(1,1),then further modified the result using the weighted Markov chain,and at the end,through an empirical case,proved the accuracy of the model over the GM(1,1).

grey forecasting;Markov;airway freight transportation volume;forecasting

F562；F224

A

1005-152X(2015)10-0127-04

2015-08-25

潘开灵（1961-），男，湖北武汉人，教授，博士生导师，博士，研究方向：管理协同理论及其应用、企业战略管理、生产组织管理；尤佳滢（1989-），女，湖北武汉人，武汉科技大学研究生，研究方向：物流技术与管理。

10.3969/j.issn.1005-152X.2015.10.035