陀螺仪中频电源特定谐波消除技术研究

林鋆各， 王俊雄， 黄 浩

(1.上海交通大学海洋工程国家重点实验室，上海200030；2.海军九〇二工厂，上海200083)

陀螺仪中频电源特定谐波消除技术研究

林鋆各1， 王俊雄1， 黄 浩2

(1.上海交通大学海洋工程国家重点实验室，上海200030；2.海军九〇二工厂，上海200083)

500 Hz中频逆变电源是某舰船陀螺仪必不可少的供电设备，要求电压、频率稳定，输出正弦波质量高。通过建立三相逆变器的SHEPWM数学模型，研究了求解开关角的同伦牛顿算法及初值给定规律；并通过Matlab/Simulink仿真对SPWM调制与SHEPWM调制的谐波进行了对比分析。所得结果验证了SHEPWM技术能够使逆变电源具有良好的谐波抑制特性。

逆变电源；特定谐波消除技术；同伦牛顿算法

陀螺仪是通过敏感地球自转的水平分量来测定仪器架设点真北方位的精密仪器，已被广泛地应用于各类大、中、小型舰艇、远洋运输船、渔船、海洋工程船和科考船，是惯性导航系统中不可缺少的重要组成部分。陀螺供电电源一般为中频(本文中研究的为500 Hz)的单相或者三相交流电源。同时，这类电源广泛应用于航空航天、舰船、机车、感应加热以及雷达、通信交换机等设备中。因此，对这类电源的研究具有很高的工程实用价值。为了提高陀螺仪的测量精度，对陀螺电源电压、频率稳定度、输出正弦波质量均提出了较高的要求。谐波的存在容易产生有害力矩，对负载和电源逆变器本身都会造成剧烈的不稳定影响。为此，必须减小输出谐波，获得高质量的正弦波。

特定谐波消除技术(SHET)是由Patel H.S.和Hoft R.G.于1973年提出的[1]。采用SHET的PWM技术称为特定谐波消除脉宽调制(SHEPWM)技术。与其他PWM技术相比，SHEPWM技术具有能消除特定的低次谐波，降低逆变器开关频率，减少电流脉动，输出波形质量高等优点，因此对SHEPWM技术的研究具有明显的理论意义和广阔的工程开发前景。本文建立三相逆变器的SHEPWM数学模型，研究了求解开关角的同伦牛顿算法及初值给定规律；并通过Matlab/Simulink仿真对SPWM调制与SHEPWM调制的谐波进行了对比分析。

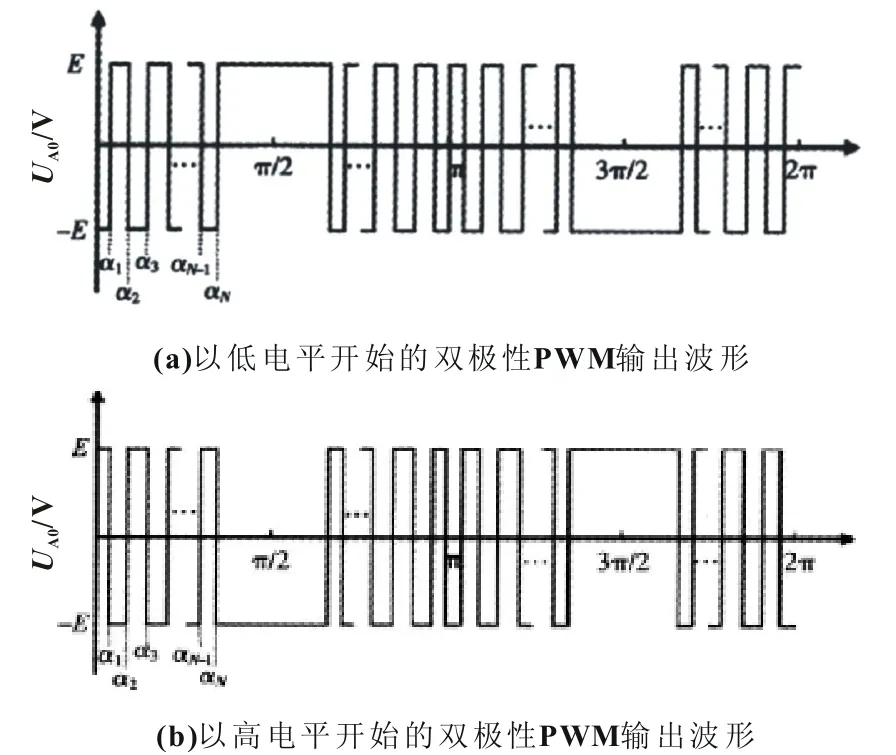
图1 双极性PWM输出波形

1 SHEPWM的数学模型

采用PWM控制的逆变器常用傅里叶级数来分析其谐波成分[2]。以双极性SHEPWM为例，图1为已知开关角的双极性PWM输出波形。

对图1所示波形进行傅里叶分解得：

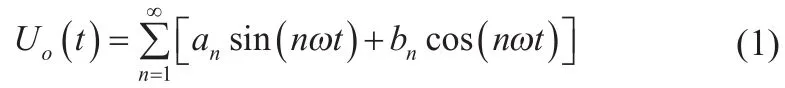
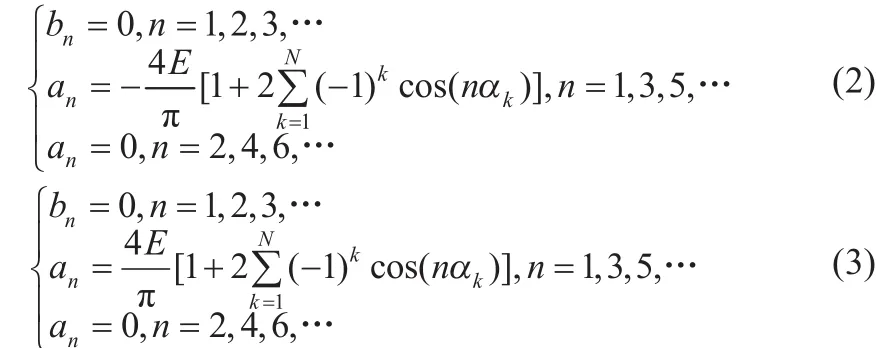
对三相对称系统而言，三的整数倍次谐波因同相而被抵消。如果令(=α1/)为给定的基波幅值，而令其他-1个低阶的高次谐波的幅值为零，则有：

式(4)即为双极性三相SHEPWM逆变器输出的数学模型。求解方程组(4)，则可得到一组在[0,π/2]区间内的开关角，这些开关角应满足以下条件：

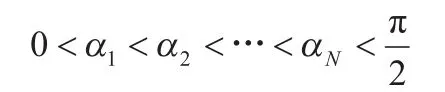
2 开关角求解方法的研究

方程组(4)为非线性超越方程组，不可能求出它的解析解，一般采用牛顿迭代法得到一组数值解。但牛顿迭代法对初值的选取要求较为严格，即要求初始近似解α0与解α*充分靠近，才能使迭代数列{α*}收敛于α*。如果初值α0选取不合适，就会导致求解速度降低，甚至不收敛。实际计算中，要找到满足要求的迭代初始值往往比较困难。因此，文献[3]采用了同伦算法来求解。同伦算法具有全局收敛和收敛速度快的特点，并且对初值不敏感，理论上对任意给定初始值都能使用迭代收敛，但在迭代步数较小时，计算结果不够准确。为此文献[4]采用同伦牛顿算法，即将牛顿算法和同伦算法结合，克服了牛顿迭代算法收敛域窄和同伦算法计算结果不够准确的缺点，从而使计算在大范围内快速收敛于精确解。

尽管理论上同伦牛顿算法对初值没有严格要求，即对任意初值都能收敛，但如果初值选取不当，仍然会导致计算次数增加，求解时间延长，甚至可能会导致不收敛。而适当选取初值，可以加快收敛速度，缩短求解时间，故对同伦牛顿法进行初值选取的研究。

对于三相双极性逆变器来说，经过分析与计算，得到的以下初值给定规律，在=0.1～1.15内均适用：

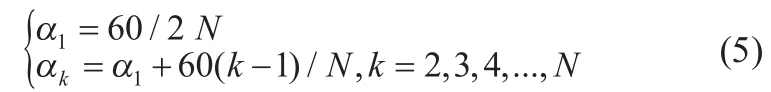
通过计算发现(表1)，对于三相双极性逆变器来说，输出相电压波形与图1(a)对应时，开关角个数采用奇数，输出相电压波形与图1(b)对应时，开关角个数采用偶数，能使方程组迭代求解的收敛性增强。表中为同伦迭代的次数，为牛顿迭代的次数。

表1 不同N值的收敛性比较

因此，采用同伦牛顿算法求解特定消谐方程组，并且在给定适当的初值的情况下，具有收敛范围大和收敛速度快的优点，同时保证了求解结果的精确性。

3 SPWM与SHEPWM谐波对比分析

假定SPWM(正弦脉宽调制)调制波为正弦波，则其调制度与SHEPWM的具有相同意义，可用同一符号表示。当SPWM的载波比=21与SHEPWM的开关角数=10时，两种PWM方法在一周内开关次数均为21。在相同开关频率前提下，使用Matlab/Simulink仿真，并对二者谐波含量进行对比分析。

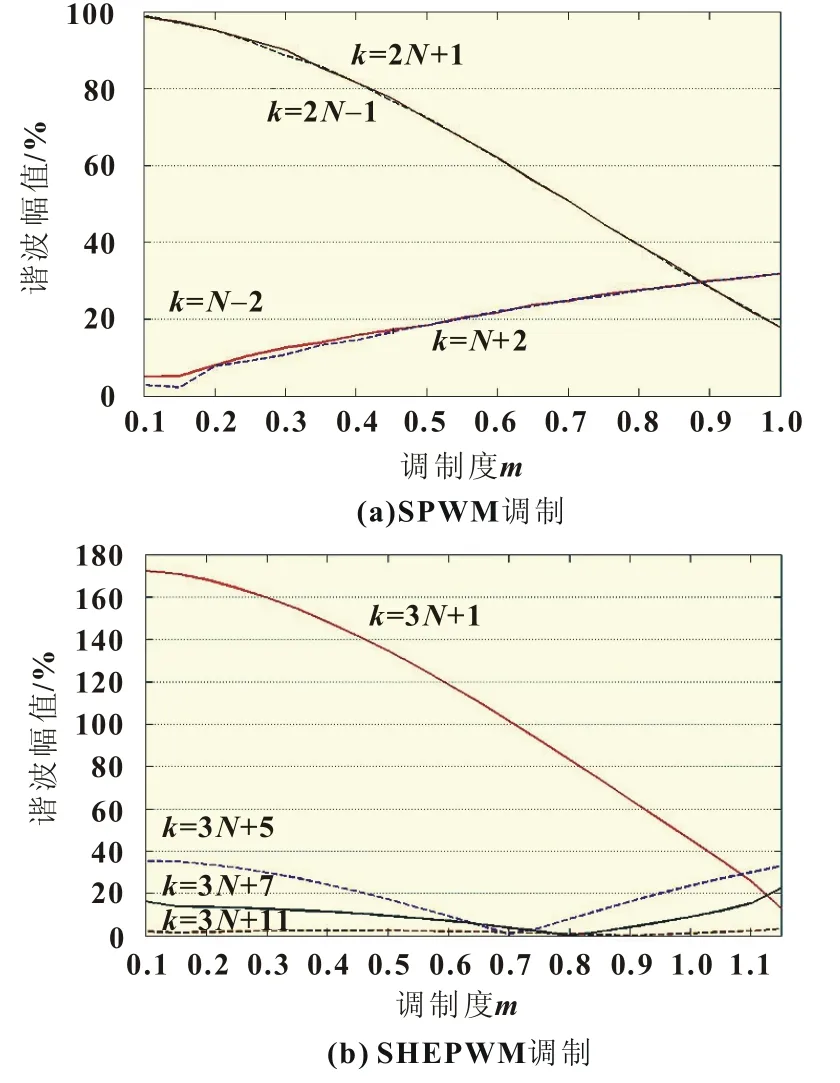
图2 各次谐波幅值与调制度的关系

从图2(a)可以看出SPWM调制的低次谐波为19次、23次，二者幅值接近。从图2(b)中可以看出SHEPWM调制的低次谐波为31次、35次，虽然次数高于前者，对降低谐波影响有利，但31次谐波值在的大部分区间内也大于前者。图2(b)同时表明在SHEPWM调制时，3+1次谐波最为突出；3+5次谐波为第二大谐波，其幅值在≈0.7时有一个接近于零的极小值，当＞1.1时，其幅值大于3+1次谐波；3+7次谐波值在0＜＜1.1范围内较小，当＞1.1后急速上升。因此，设计滤波器时，在0＜＜1.1的范围内应该着重抑制3+1次与3+5次谐波，而当＞1.1后还应兼顾抑制3+7次谐波。

同时，还必须考虑相近次数谐波的迭加作用，以及两种调制法的谐波幅值随变化的不同规律。然而直观判断出两种PWM谐波总影响的相对大小有一定的困难。通常，采用对所有谐波求总谐波畸变率的办法，由此来确定谐波的总体影响。定义如下[5]：

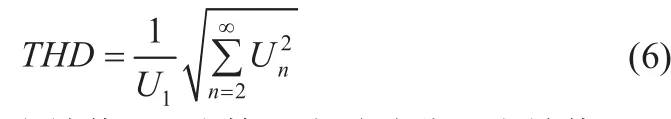
式中：U1为基波分量有效值；Un为第n次谐波分量有效值。3示出了SPWM与SHEPWM在∈[0,1.15]区间内的线电压THD曲线(累计谐波至90次)。结果表明，在m∈[0,1]区间，SHEPWM的THD大于SPWM的THD；而m＞1后，转为低于SPWM在m=1时的THD值(68.06%)。当M=1.15时，SHEPWM的THD仅为57.86%。

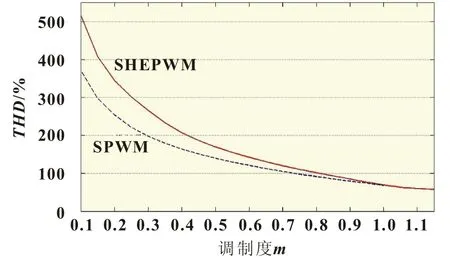
图3 THD值与m的关系

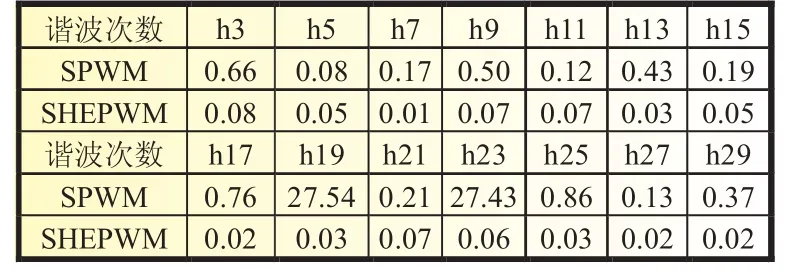
表2 低次谐波幅值对比

(1)消除了特定的低次谐波，因此电流脉动大大减少，逆变电源的性能得以提高；

(2)通过调制可以提高变频电源的效率，节约能源，其基波电压最大幅值可以达到1.15倍的直流侧电压，这是SPWM所不容易通过直接调制载波幅值达到的；

(3)在中高频时，由于开关次数不能太高，故SPWM谐波的频率范围受到限制，而SHEPWM则能够使功率器件的开关频率下降约三分之一，降低开关损耗。

4 结论

本文建立三相逆变器的SHEPWM数学模型，研究了求解开关角的同伦牛顿算法及初值给定规律；并通过Matlab/ Simulink仿真，对SPWM与SHEPWM的谐波进行了对比分析。采用SHEPWM技术能够使逆变电源具有良好的谐波抑制特性，能够从根本上解决谐波抑制问题。随着DSP等处理芯片的快速发展，通过软件、硬件的设计，可使SHEPWM这一很有前景的技术尽快走向实用化。

[1]PATEL H S,HOFT R G.Generalized technique of harmonic elimination and voltage control in thyristor inverter:Part1——Harmonic elimination[J].IEEE-IA,1973,9(3):301-317.

[2]陈道炼.DC-AC逆变技术及其应用[M].北京：机械工业出版社，2003:48-49.

[3]谢运祥，周炼，彭宏.逆变器消谐PWM模型的同伦算法研究[J].中国电机工程学报，2000,20(10):23-26.

[4]潘高强.逆变器PWM谐波分析及谐波抑制方法研究[D].沈阳：沈阳工业大学，2010.

[5]陈坚，康勇.电力电子学[M].北京：高等教育出版社，2011：95.

Research on selected harmonic elimination technique for medium frequency power inverter of gyroscope

Medium frequency 500Hz power inverter was an essential part of a ship's gyroscope power supply unit, which required stable output voltage and frequency,and high quality of sinusoidal output waveform.The SHEPWM mathematical model of three-phase inverter was established;the homotopy Newton algorithm was studied;and rule of switching angles solving was given. Harmonic for SPWM modulation and SHEPWM modulation through MATLAB/simulink simulation were comparative analyzed.The results prove the SHEPWM technique enables power inverter to have good harmonic suppression characteristics.

inverter;selected harmonic elimination technique;homotopy Newton algorithm

TM 464

A

1002-087 X(2015)10-2247-03

2015-03-16

林鋆各(1989—)，女，广西省人，硕士生，主要研究方向为动力装置及自动化。