基于蒙特卡洛法的EV充电负荷多目标随机规划

2015-08-01王志刚余保庆付婷婷

电源技术 2015年10期

李锰，王志刚，余保庆，付婷婷，吕源

(1.国网河南省电力公司经济技术研究院，河南郑州450052；2.国网河南省电力公司驻马店供电公司，河南驻马店463000；3.郑州电力高等专科学校，河南郑州450000)

李锰1，王志刚2，余保庆2，付婷婷3，吕源2

分析了现有电动汽车(electric vehicle，EV)充电负荷优化方式和算法的不足，结合配电系统最优运行的要求，考虑了多个随机因素的影响，以电动汽车蓄电池满充、蓄电池充电功率不越限及配网潮流约束等作为约束条件，以配电网网损、电源节点负荷峰值、负荷波动情况优化为子目标，建立了新的基于EV充电负荷的配电网多目标随机优化模型。利用改进的非支配排序遗传算法-Ⅱ(non-dominated sorting genetic algorithm-2，NSGA-2)求解，采用IEEE-33节点配电系统的实际优化状况为例进行了蒙特卡洛仿真。仿真证明所提出的EV充电负荷多目标优化策略在更贴近实际的随机模型下仍可以有效减弱电动汽车大规模接入对电网的冲击，充分利用其可控性实现配网各项指标的经济运行。

电动汽车；充电负荷；多目标优化；非支配排序遗传算法；蒙特卡洛仿真

电动汽车由于不直接消耗化石能源可以有效地减小CO2的排放，并降低车主费用等方面的优势得到了政府和企业的青睐，相关研究取得了巨大进展[1]，预计到2015年新购车辆中将有10%是混合动力汽车，不断增长的电动汽车将给电网增加18%的负荷，电动汽车大规模推广的同时也将对接入配网带来较大的冲击。

对此，国内外学者对电动汽车的充电行为做了大量的研究[2-6]。文献[2]认为可将EV视为大容量分布式储能，来应对新能源波动性输出带来的问题；文献[3]分析了调度EV充电负荷以平滑电网负荷波动，消纳夜间过剩风电的可能性；文献[4]认为EV有序充电可以提高由于调频、调压及负荷波动带来的电网效率过低问题；相关文献均认为对EV充电负荷的优化控制可以有效降低EV大规模应用对配网的冲击，同时利用自身的特性可实现对电网运行优化，对此，文献[5]建立了电动汽车充电的两阶段优化模型，第一阶段优化系统峰荷，第二阶段优化负荷波动，并利用整数规划求解提出的优化模型，但未考虑电动汽车充电时间的随机性及其与初始时刻EV电池荷电状态(state of charge，SOC)的关系，与实际不符；文献[6]根据不同类型电动汽车的使用特点，仿真分析了随机充、放电负荷曲线，但没有系统地分析大量电动汽车充放电过程对系统运行的影响且将起始充电时间假设为服从均匀分布的假设过强；文献[7]提出了多种EV有序充电方法，但充电开始时刻与初始SOC均采用高斯分布表示，不能有效反映实际充电负荷状态；文献[8]利用峰谷电价诱使EV在波谷充电，实现了对配网负荷的“削峰填谷”，但峰谷电价是否会对EV充电行为产生影响或者产生怎样的影响尚无定论；文献[9]以最小化配网网损为目标建立了EV充电优化模型，并利用迭代修正节点电压法求解模型，仿真证明有序充电不仅可有效降低网损还能平抑负荷改善电压水平，但提出的策略优化目标过于单一且将初始SOC设为0.1，并假定电动汽车充电行为完全可控，忽略了随机性。

综上，现有EV充电负荷优化策略还存在各种各样的问题，本文假设配网中每个节点处皆有一EV智能充电站[10]，在满足全部EV蓄电池满充至90%以上、EV初始SOC根据行驶里程随机分布、充电功率不越限、线路潮流约束等不规范约束条件下，通过优化EV各时段充电功率，实现优化负荷波形、降低网损等多目标优化目的，并利用蒙特卡洛仿真证明了提出的EV充电负荷优化策略的有效性，由于仿真基于随机分布，所得出的结论更具实际意义与应用价值。

1 配网多目标优化模型

1.1 汽车剩余荷电状态与返家时间分布

通过对统计数据的数理估计可得汽车的日行驶里程服从对数正态分布[11]：

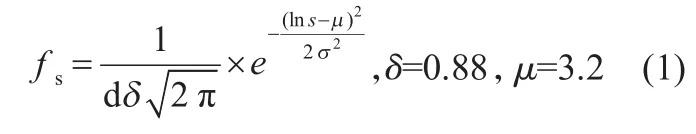
EV电池的剩余荷电状态：S OC =1-s。

文章选用丰田公司RAV4电动汽车进行仿真，RAV4的电池组容量为s27.4 kWh，单位kWh电量可行驶4.02 km，则SOC=1-110。

由概率论知识可计算得EV到家时电池的剩余荷电状态SOC满足分布：

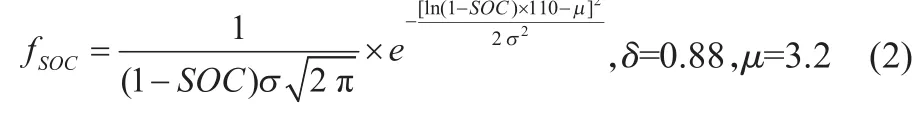
假设汽车最后一次返家后立即接入智能汽车充电站，则从这一时刻到再次离开家这段时间，EV处于可调度状态，利用最大似然估计对统计数据估计，求得EV最后一次返家时间满足分布：

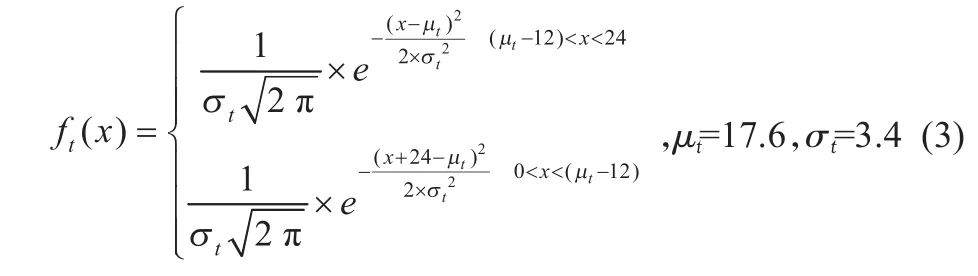
1.2 优化子目标选择

为减小EV充电负荷接入配网的冲击作用，并利用其可控性达到削峰平谷及与新能源协调运行等目的，选择EV充电负荷优化目标为：

(1)整个优化周期内网损最小

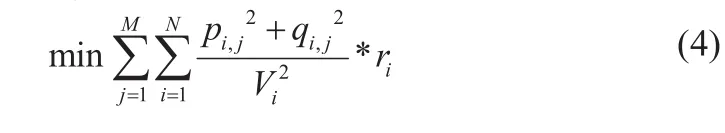
等式约束为潮流约束：

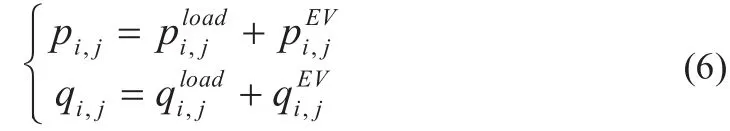
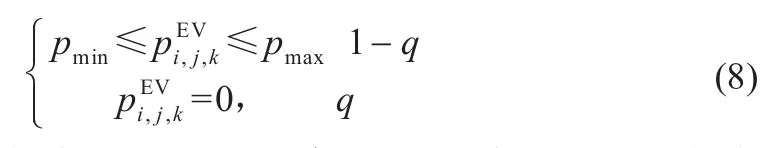
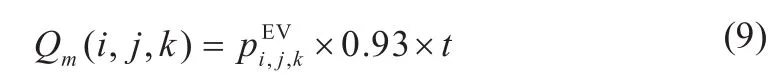
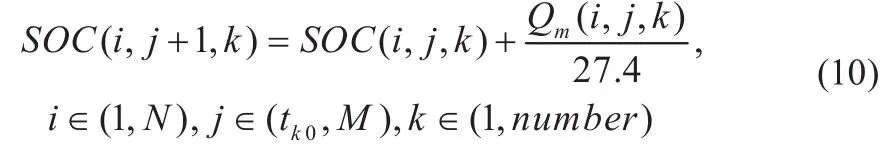
(2)整个优化周期内流过电源节点的负荷峰值最小

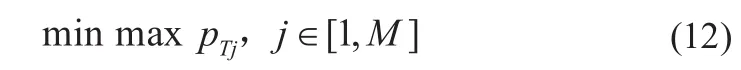
(3)整个优化周期内电源节点的负荷波动最小

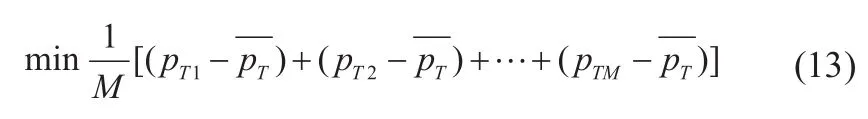
综上，基于EV充电负荷的优化可以用数学描述为如下多目标多约束优化问题：

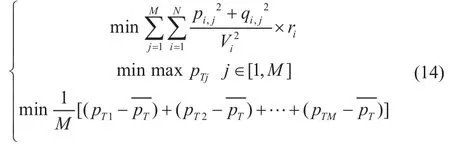
S.t(约束条件)：

其中，式(14)为基于EV充电负荷的配网多目标优化的目标函数表达式，式(15)与配网潮流约束方程一起构成了该多目标优化的约束函数。

1.3 算法的选择与改进

针对该多目标优化问题，选择实数编码的非支配排序遗传算法NSGA-2求其Pareto解集，相关参数如表1所示，优化对象为第个优化时段第条支路末端节点接入的第辆EV的充电功率,,EV。

表1 NSGA-2的相关参数

(1)算法选择多项式变异算子及模拟二进制交叉(simulated binary crossover，SBX)算子执行进化操作，并利用联赛法选择较优个体进入下一代，联赛规模取为种群大小的一半，为避免机器时间的浪费，在固定遗传代数的终止条件下，增加新的循环终止条件：当连续5代进化操作得到的非支配解集合内所有个体对三个子目标的平均适应度都不小于之前得到的Pareto解集的最小适应度时，即认为算法已经收敛到了Pareto最优解，终止循环。

(2)优化起始时段(7:00到22:00)，原始负荷曲线维持在一个较高的水准，因此在这一时段应以较大的概率1使得EV充电功率为0，而在余下的时段以较小的概率2使EV充电功率为0加速EV充电，为此设置启发算子：

(3)对于约束的处理：在原有染色体串上添加一约束违背惩罚位对违背节点电压约束的染色体较大惩罚对违背 SOC约束的染色体分段惩罚或时，时时为惩罚系数，随着遗传代数增大而增大。

(4)约束违背惩罚位在算法中的作用：重新定义pareto优胜：对于个体和，当且仅当对于所有个子目标成立，且至少存在一个∈使得成立，且成立，才能使得个体优于个体。其中为第个个体对第个子目标的适应值。

2 仿真计算

2.1 优化配电网参数

选择IEEE-33节点配电网络作为EV充电负荷优化的仿真环境，优化周期取一天(24 h)，根据驾驶习惯，EV用户一般从早晨7:00开始陆续使用汽车，故优化时间选为当日7:00至第二日7:00，并按小时分为24个优化时段，在每一个优化时段内EV充电功率保持恒定(图1)。

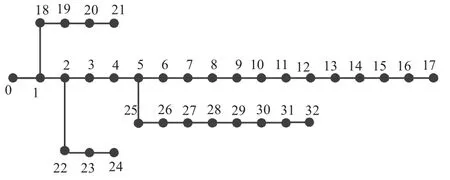
图1 IEEE-33节点配电系统拓扑结构

图中，节点0为电源节点，节点6、7、14、23、24、29、31为恒功率节点，其余节点负荷由典型居民负荷叠加分布为[0，(0.1)2]的随机变量得到的模拟负荷与相应节点的等效用户数相乘得到(为日负荷峰值)，各节点功率、支路阻抗、等效居民数、功率因数等参数见附表1，网络首段基准电压12.66 kV，三相功率基准值取10 MVA。图2为居民典型日负荷曲线。

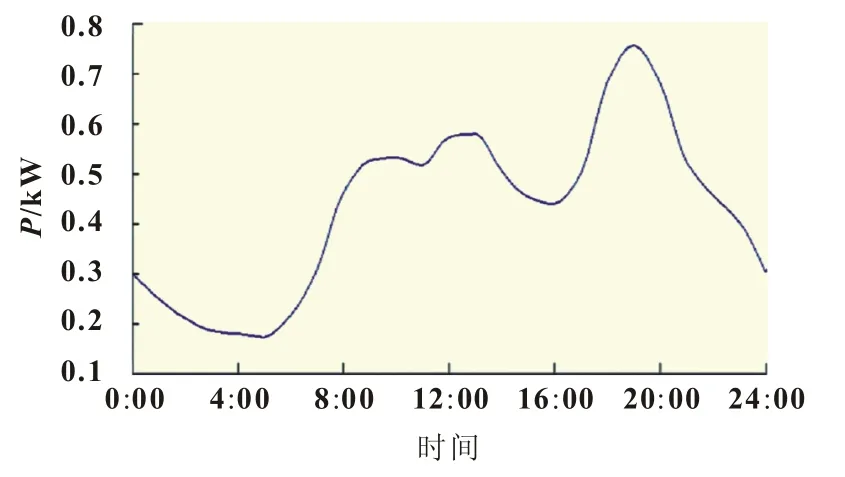
图2 居民典型日负荷曲线

定义EV渗透率为有EV用户在居民中所占比例：

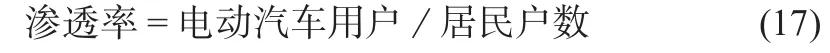
根据式(17)及附表1中各节点等效用户数可得相应渗透率下各节点接入EV数，然后根据式(2)及(3)可得EV并入该节点的时间及并入时刻的SOC大小。

分别对以下三种情况进行仿真计算，得出电源节点负荷曲线，以及相应EV充电状态下的的配网网损、电源节点负荷峰值和负荷方差大小等，对比其结果：

(Ⅰ)接入各节点的EV从最后一次返家时刻开始，即以最大充电功率4 kW进行充电，直至充满为止，称为EV的无序充电状态。

(Ⅱ)基于本文提出的充电模型，只考虑子目标(2)、(3)，相应节点EV充电功率以改进NSGA-2算法优化得到的最优解所示充电策略进行充电，称为EV的两目标充电状态。

(Ⅲ)基于本文提出的充电模型，考虑所有三个子目标，相应节点EV充电功率以改进NSGA-2算法优化得到的最优解所示充电策略进行充电，称为EV的最优充电状态。

2.2 仿真结果分析

设EV渗透率为0.35，运行仿真得到的Pareto最优解集如图3所示。

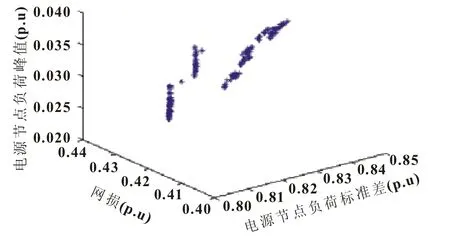
图3 NSGA-2优化得到的pareto解集

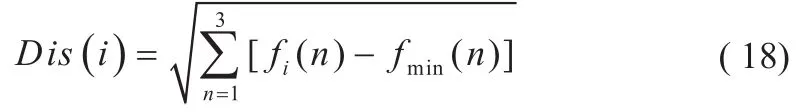
选择Dis(i)最小的个体所示解为最优解，其对应的充电策略为多目标优化条件下EV的最优充电策略，图形化最优充电策略、两目标充电策略及无序充电策略下电源节点的功率曲线如图4所示。

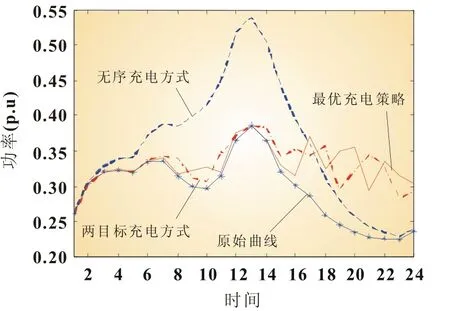
图4 无序充电、两目标充电及最优充电策略对应的电源节点负荷曲线

由图4可以看出，如果不对EV充电负荷进行控制，将在原负荷曲线上形成更大的负荷峰，进一步拉大峰谷差，对配网稳定性及传输功率造成更大压力；而两目标充电策略及最优充电策略在负荷峰值附近大幅减小EV充电功率甚至不充电，而在负荷较低时增大充电功率，有效地实现了负荷的转移达到了“削峰平谷”平滑负荷曲线的目的。

EV无序充电状态、两目标充电策略、最优充电策略及不考虑EV充电负荷时，系统各项参数对比如表2(各充电策略均在随机条件下利用蒙特卡洛仿真500次，参数取自500次模拟中最差状况)。

表2 不同情况下IEEE-33配网参数

由表2可知，最优充电策略较无序充电及两目标充电策略有效地降低了网损，最优充电策略及两目标充电策略下电源节点负荷峰值与不考虑EV充电均相等，与EV无序充电相比二者均最小化了EV充电负荷的影响；两目标充电策略下负荷波动较最优充电策略有略微减小，二者较其余两种充电情况负荷波动均大幅减小；但较最优充电策略，两目标充电策略下节点电压水平较低，但在500次仿真中并没发生电压越限情况；无序充电状态下，节点电压在19:00附近时由于大量电动汽车接入网络并立即开始充电，负荷峰值显著增大，节点16、17的电压都有越限的危险(0.932 2 p.u，0.931 7 p.u)，且整个周期内的系统网损较有序充最优电状态增加了约19.9%，较两目标充电状态增加了16.4%。

相较两目标优化策略，最优充电策略下电源节点负荷波动稍大，但节点电压水平较高、网损较小。这一方面说明减小电源节点负荷波动(子目标3)与降低网损(子目标1)并不具有一致性，另一方面也表明本文最优充电策略设置“三目标”的必要性与准确性。

由以上分析，本文提出的EV最优充电策略可以有效降低EV充电负荷对配网带来的影响，并利用充电负荷改善配网负荷波形，提高节点电压水平，减小网损，维持系统稳定等。

3 结论

随着电动汽车行业的发展，规模化EV负荷的接入给配电系统的安全、优质、经济运行带来严峻的挑战。本文提出基于EV充电负荷的配网多目标优化策略来改善电力系统运行的安全性和经济性，在考虑随机因素的前提下，以IEEE-33节点配电系统中EV充电为例进行测试，结果表明：优化之后的EV充电方式，在保证EV蓄电池满充的前提下，使配网运行情况得到极大改善。相较EV无序充电方式，运行情况不仅没有因EV的大规模接入而恶化反而利用其充电负荷的可控性优化了节点负荷波形使有功波动更小、网损更低、电网更加稳定，同时减少了系统备用容量。

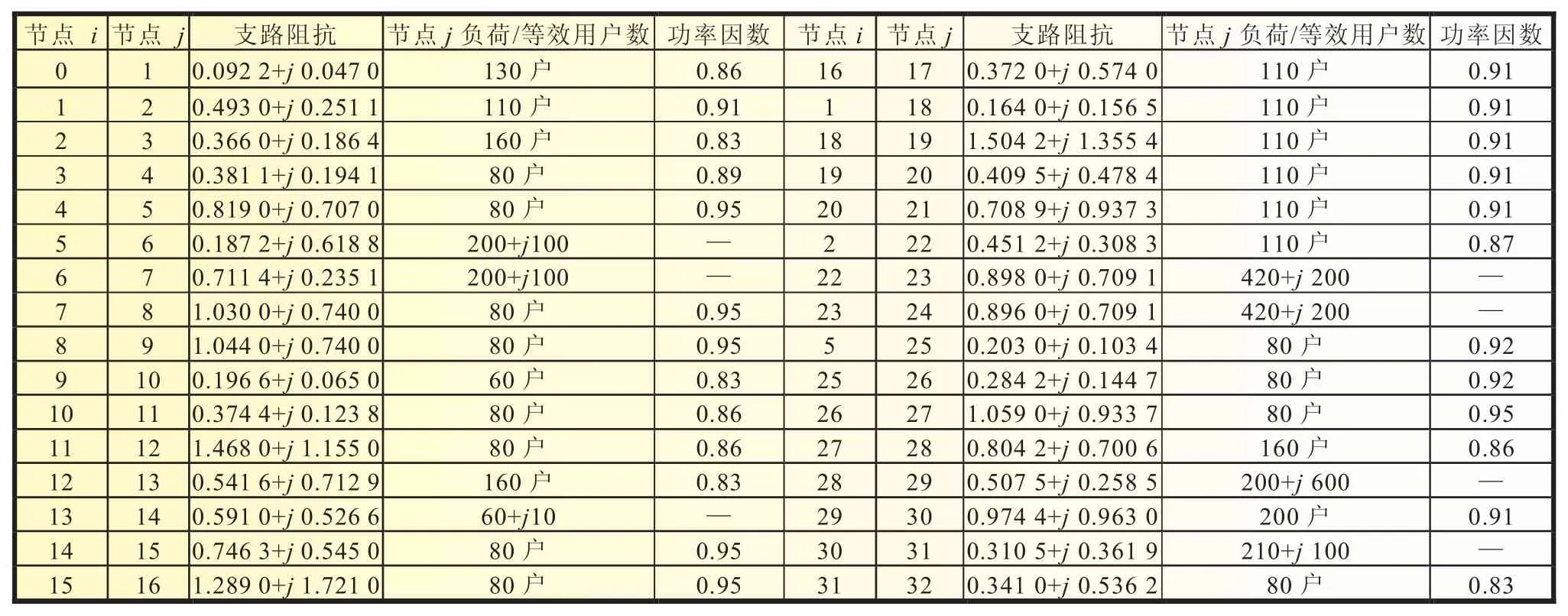
附表1：

[1]DAEHYUN B,MICHAILIDIS G,DEVETSIKIOTIS M.Demand response control for PHEV charging stations by dynamic price adjustments[C]//2012 IEEE PES Innovative Smart Grid Technologies. Piscataway,NJ,United States:IEEE,2012:1-8.

[2]KADUREK P,IOAKIMIDIS C,FERRAO P.Electric Vehicles and their impact to the electric grid in isolated systems[C]//2009 International Conference on Power Engineering,Energy and Electrical Drives.Piscataway,NJ,United States:IEEE,2009:49-54.

[3]于大洋，宋曙光，张波，等.区域电网电动汽车充电与风电协同调度的分析[J].电力系统自动化，2011,35(14):24-29.

[4]刘晓飞，张千帆，崔淑梅.电动汽车V2G技术综述[J].电工技术学报，2012,27(2):121-126.

[5]罗卓伟，胡泽春，宋永华，等.大规模电动汽车充放电优化控制及容量效益分析[J].电力系统自动化，2012,36(10):19-26.

[6]杨洪明，熊脶成，刘保平.插入式混合电动汽车充放电行为的概率分析[J].电力科学与技术学报，2010,25(3):8-12.

[7]唐升卫.电动汽车有序充电研究[D].长沙：湖南大学，2012.

[8]葛少云，黄镠，刘洪.电动汽车有序充电的峰谷电价时段优化[J].电力系统保护与控制，2012,40(10):1-5.

[9]占恺峤，宋永华，胡泽春，等.以降损为目标的电动汽车有序充电优化[J].中国电机工程学报，2012,32(31):11-18.

[10]李瑞生，王晓雷，周逢权，等.灵巧潮流控制的电动汽车智能化充电站[J].电力系统保护与控制，2010,38(21):87-90.

[11]田立亭，史双龙，贾卓.电动汽车充电功率需求的统计学建模方法[J].电网技术，2010,34(11):126-130.

[12]王辉，文福拴，辛建波.电动汽车充放电特性及其对配电系统的影响分析[J].华北电力大学学报，2011,38(5):17-24.

Multi-objective optimization strategy of EV’s charging load based on Monte-Carlo simulation

The influence of charging of electric vehicles(EV)on distribution systems was studied.According to the analysis on the existing electric vehicle's charging load optimization approach and algorithms,the new multi-objective optimization model of charging load was established,the demand of distribution system's operation was also taken into account,the state of charge,the power of charging and the constrained load flow was taken as constrain,the transmission loss,load peak,fluctuation of load was taken as the multi-objective.Non-dominated sorting genetic algorithm-2(NSGA-2)was used to solve the model,the IEEE-33 node distribution system was taken as an example of the Monte Carlo simulation,and the distribution grid operating parameters were compared with disordered charging state.The simulation results certify the multi-objective optimization strategy minimize the impulse of large scale used of EV,and benefit the optimizing operation of distribution grid taking advantage of its controllability.

electric vehicle;charging load;multi-objective optimization;non-dominated sorting genetic algorithm-2; Monte-Carlo simulation

TM 721

1002-087 X(2015)10-2208-04