有关7m＋j型奇正整数不是完全数的一些命题

张四保

（喀什师范学院数学系，新疆喀什 844008）

有关7m＋j型奇正整数不是完全数的一些命题

张四保

（喀什师范学院数学系，新疆喀什 844008）

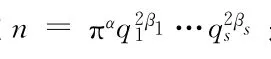
完全数；奇完全数；命题

0 引言

虽未解决是否存在奇完全数的问题，但有关奇完全数存在热点问题：一，奇完全数的大小估计，其研究成果参考文献［3－5］；二，奇完全数相异素因子大小估计与个数估计，其研究成果参考文献［6－10］；三，特殊类型奇数是否是完全数问题，其研究成果参考文献［11－14］.

1 主要结论

（1）当π≡3，5，6（mod 7）；

（2）当π≡2，4（mod 7）且α＝4k＋1，k2（mod 3），则n不是完全数.

当π≡1（mod 7）时，显然有πα≡1（mod 7）.

当π≡2（mod 7）时，有πα≡24k＋1（mod 7）.当k≡0（mod 3），则πα≡2（mod 7）；当k≡1（mod 3），则πα≡4（mod 7）；当k≡2（mod 3），则πα≡1（mod 7）.

当π≡3（mod 7）时，有πα≡34k＋1（mod 7）.当k≡0（mod 3），则πα≡3（mod 7）；当k≡1（mod 3），则πα≡5（mod 7）；当k≡2（mod 3），则πα≡6（mod 7）.

当π≡4（mod 7）时，有πα≡44k＋1（mod 7）.当k≡0（mod 3），则πα≡4（mod 7）；当k≡1（mod 3），则πα≡2（mod 7）；当k≡2（mod 3），则πα≡1（mod 7）.

当π≡5（mod 7）时，有πα≡54k＋1（mod 7）.当k≡0（mod 3），则πα≡5（mod 7）；当k≡1（mod 3），则πα≡3（mod 7）；当k≡2（mod 3），则πα≡6（mod 7）.

当π≡6（mod 7）时，有πα≡64k＋1≡6（mod 7）.

（1）当π≡3（mod 7）时，有πα≡3，5，6（mod 7），这与πα≡1（mod 7）矛盾；当π≡5（mod 7）时，有πα≡3，5，6（mod 7），这与πα≡1（mod 7）矛盾；当π≡6（mod 7）时，有πα≡6（mod 7），这与πα≡1（mod 7）矛盾，因而n不是完全数.

（2）π≡2（mod 7）且α＝4k＋1，当k≡0（mod 3）时，有πα≡2（mod 7），这与πα≡1（mod 7）矛盾；当k≡1（mod 3），则πα≡4（mod 7），这与πα≡1（mod 7）矛盾，因而n不是完全数.

π≡4（mod 7）且α＝4k＋1，当k≡0（mod 3）时，有πα≡4（mod 7），这与πα≡1（mod 7）矛盾；当k≡1（mod 3），则πα≡2（mod 7），这与πα≡1（mod 7）矛盾，因而此时n不是完全数.

证毕.

（1）当π≡1，3，5，6（mod 7）；

（2）当π≡2（mod 7）且α＝4k＋1，k1（mod 3）；

（3）当π≡4（mod 7）且α＝4k＋1，k0（mod 3），则n不是完全数.

（1）当π≡1，3，5，6（mod 7）；

（2）当π≡2（mod 7）且α＝4k＋1，k0（mod 3）；

（3）当π≡4（mod 7）且α＝4k＋1，k1（mod 3），则n不是完全数.

由命题1至命题3，可得到推论1.

（1）当π≡1，3，5，6（mod 7）；

（2）当π≡2（mod 7）且α＝4k＋1，k0（mod 3）；

（3）当π≡4（mod 7）且α＝4k＋1，k1（mod 3），

则n不是完全数.

由命题1的讨论可知，当π≡1（mod 7）时，有πα≡1（mod 7）；当π≡3（mod 7）时，有πα≡3，5，6（mod 7）；当π≡5（mod 7）时，有πα≡3，5，6（mod 7）；当π≡6（mod 7）时，有πα≡6（mod 7）.由此可知，当π≡1，3，5，6（mod 7）时，πα取模7的情况与πα≡2（mod 7）矛盾，因而n不是完全数.

π≡2（mod 7）且α＝4k＋1，当k≡1（mod 3）时，有πα≡4（mod 7），这与πα≡2（mod 7）矛盾；当k≡2（mod 3），有πα≡1（mod 7），这与πα≡2（mod 7）矛盾，因而n不是完全数.

π≡4（mod 7）且α＝4k＋1，当k≡0（mod 3）时，有πα≡4（mod 7），这与πα≡2（mod 7）矛盾；当k≡2（mod 3），有πα≡1（mod 7），这与πα≡2（mod 7）矛盾，因而n不是完全数.

证毕.

（1）当π≡3，5，6（mod 7）；

（2）当π≡2，4（mod 7）且α＝4k＋1，k2（mod 3），

则n不是完全数.

（1）当π≡1，3，5，6（mod 7）；

（2）当π≡2（mod 7）且α＝4k＋1，k1（mod 3）；

（3）当π≡4（mod 7）且α＝4k＋1，k0（mod 3），

则n不是完全数.

由命题4至命题6，可得到推论2.

（1）当π≡1，2，4，6（mod 7）；

（2）当π≡3（mod 7）且α＝4k＋1，k0（mod 3）；

（3）当π≡5（mod 7）且α＝4k＋1，k1（mod 3），

则n不是完全数.

由命题1的讨论可知，当π≡1（mod 7）时，有πα≡1（mod 7）；当π≡2（mod 7）时，有πα≡1，2，4（mod 7）；当π≡4（mod 7）时，有πα≡1，2，4（mod 7）；当π≡6（mod 7）时，有πα≡6（mod 7）.由此可知，当π≡1，2，4，6（mod 7）时，πα取模7的情况与πα≡3（mod 7）矛盾，因而n不是完全数.

π≡3（mod 7）且α＝4k＋1，当k≡1（mod 3）时，有πα≡5（mod 7），这与πα≡3（mod 7）矛盾；当k≡2（mod 3），有πα≡6（mod 7），这与πα≡3（mod 7）矛盾，因而n不是完全数.

π≡5（mod 7）且α＝4k＋1，当k≡0（mod 3）时，有πα≡5（mod 7），这与πα≡3（mod 7）矛盾；当k≡2（mod 3），有πα≡6（mod 7），这与πα≡3（mod 7）矛盾，因而n不是完全数.

证毕.

（1）当π≡1，2，4，6（mod 7）；

（2）当π≡3（mod 7）且α＝4k＋1，k1（mod 3）；

（3）当π≡5（mod 7）且α＝4k＋1，k0（mod 3），

则n不是完全数.

（1）当π≡1，2，4（mod 7）；

（2）当π≡3，5（mod 7）且α＝4k＋1，k2（mod 3），

则n不是完全数.

由命题7至命题9，可得到推论3.

（1）当π≡1，3，5，6（mod 7）；

（2）当π≡2（mod 7）且α＝4k＋1，k1（mod 3）；

（3）当π≡4（mod 7）且α＝4k＋1，k0（mod 3），

则n不是完全数.

由命题1的讨论可知，当π≡1（mod 7）时，有πα≡1（mod 7）；当π≡3（mod 7）时，有πα≡3，5，6（mod 7）；当π≡5（mod 7）时，有πα≡3，5，6（mod 7）；当π≡6（mod 7）时，有πα≡6（mod 7）.由此可知，当π≡1，3，5，6（mod 7）时，πα取模7的情况与πα≡4（mod 7）矛盾，因而n不是完全数.

π≡2（mod 7）且α＝4k＋1，当k≡0（mod 3）时，有πα≡2（mod 7），这与πα≡4（mod 7）矛盾；当k≡2（mod 3）时，有πα≡1（mod 7），这与πα≡4（mod 7）矛盾，因而n不是完全数.

π≡4（mod 7）且α＝4k＋1，当k≡1（mod 3）时，有πα≡2（mod 7），这与πα≡4（mod 7）矛盾；当k≡2（mod 3）时，有πα≡1（mod 7），这与πα≡4（mod 7）矛盾，因而n不是完全数.

证毕.

（1）当π≡1，3，5，6（mod 7）；

（2）当π≡2（mod 7）且α＝4k＋1，k0（mod 3）；

（3）当π≡4（mod 7）且α＝4k＋1，k1（mod 3），

则n不是完全数.

（1）当π≡3，5，6（mod 7）；

（2）当π≡2，4（mod 7）且α＝4k＋1，k2（mod 3），

则n不是完全数.

由命题10至命题12，可得到推论4.

（1）当π≡1，2，4，6（mod 7）；

（2）当π≡3（mod 7）且α＝4k＋1，k1（mod 3）；

（3）当π≡5（mod 7）且α＝4k＋1，k0（mod 3），

则n不是完全数.

，若下列任一条件成立：

（1）当π≡1，2，4（mod 7）；

（2）当π≡3，5（mod 7）且α＝4k＋1，k2（mod 3），

则n不是完全数.

（1）当π≡1，2，4，6（mod 7）；

（2）当π≡3（mod 7）且α＝4k＋1，k0（mod 3）；

（3）当π≡5（mod 7）且α＝4k＋1，k1（mod 3），则n不是完全数.

由命题1的讨论可知，当π≡1（mod 7）时，有πα≡1（mod 7）；当π≡2，4（mod 7）时，有πα≡1，2，4（mod 7）；当π≡6（mod 7）时，有πα≡6（mod 7）.由此可知，当π≡1，2，4，6（mod 7）时，πα取模7的情况与πα≡3（mod 7）矛盾，因而n不是完全数.

π≡3（mod 7）且α＝4k＋1，当k≡1（mod 3）时，有πα≡5（mod 7），这与πα≡3（mod 7）矛盾；当k≡2（mod 3）时，有πα≡6（mod 7），这与πα≡3（mod 7）矛盾，因而n不是完全数.

π≡5（mod 7）且α＝4k＋1，当k≡0（mod 3）时，有πα≡5（mod 7），这与πα≡3（mod 7）矛盾；当k≡2（mod 3）时，有πα≡6（mod 7），这与πα≡3（mod 7）矛盾，因而n不是完全数.

证毕.

由命题13至命题15，可得到推论5.

2 结束语

（References）：

［1］ 盖伊R K.数论中未解决的问题［M］.张明尧，译，北京：科学出版社，2006：59.

Guy R K.Unsolved problems in number theory［M］.Zhang Mingyao，trans，Beijing：Science Press，2006：59.

［2］ Dickson L E.History of theory of number［M］.Washington：Carnegie Institution of Washington，1919.

［3］ Brent R P，Cohen G L，Riele H J J.Improved techniques for lower bounds for odd perfect numbers［J］.Math Comp，1991，57（196）：857－868.

［4］ Karl K N.Remarks on the number of factors of an odd perfect number［J］.Acta Arith，1961（6）：365－374.

［5］ Slowak J.Odd perfect numbers［J］.Math Slovaca，1999，49（3）：253－254.

［6］ Pomerance C.Odd perfect numbers are divisible by at least seven distinct primes［J］.Acta.Arith，1974（25）：265－300.

［7］ Chein E Z.An odd perfect number has a least 8prime factors［J］.Notices Math Soc，1979（26）：365.

［8］ Hagis P，Cohen G L.Every odd perfect number has a prime factor which exceeds 106［J］.Math Comp，1998（67）：1323－1330.

［9］ Goto T，Ohno Y.Odd perfect numbers have a prime factor exceeding108［J］.Math Comp，2008（77）：1859－1868.

［10］ 张四保，邓勇.Numbersω（n）of distinct primes factors for a kind of odd perfect number［J］.中国科学院研究生学院学报，2011，28（4）：548－550.

Zhang Sibao，Deng Yong.Numbersω（n）of distinct primes factors for a kind of odd perfect number［J］.Journal of Graduate University of Chinese Academy of Sciences，2011，28（4）：548－550.

［11］ McDaniel W L.The non－existence of odd perfect of a certain form［J］.Arch Math，1970（21）：52－53.

［12］ Mcdaniel W L，Hagis P.Some results concerning nonexistence of odd perfect numbers of the formpαm2β［J］.The J Fibonnacci Quart，1975，13（1）：25－28.

［13］ Iannucci D E，Sorli R M.On the total number of prime factors of an odd perfect number［J］.Math Comp，2003（72）：2078－2084.

［14］ 朱玉扬.奇完全数的几个命题［J］.数学进展，2011，40（5）：595－598.

Zhu Yuyang.Several results on odd perfect numbers［J］.Advances in mathematics，2011，40（5）：595－598.

［15］ 张四保.7 m－1形的奇正整数n不是完全数的条件［J］.黑龙江大学学报：自然科学版，2014，31（4）：480－483.

Zhang Sibao.Conditions on the positive odd numbers of the form 7 m－1are not perfect number［J］.Journal of Heilongjiang Univer－sity：Natural Science Edition，2014，31（4）：480－483.

DOI 10.3969／j.issn.2095－4107.2015.01.016

O156

A

2095－4107（2015）01－0118－05

2014－10－03；编辑：关开澄

喀什师范学院校内一般课题（（14）2513）

张四保（1978－），男，硕士，副教授，主要从事数论方面的研究.

book=122,ebook=125