EMD和独立分量分析在转盘轴承故障诊断中的应用
2015-08-01赵阳陈捷洪荣晶封杨
赵阳,陈捷,洪荣晶,封杨
(南京工业大学 机械与动力工程学院,南京 210009)
转盘轴承是一种能够承受综合载荷的大型轴承,可以同时承受较大的轴向和径向载荷以及倾覆力矩,在船舶设备、工程机械、轻工机械、冶金机械、医疗机械、工业机械等行业得到了广泛应用。由于转盘轴承工作环境恶劣,使其安装、润滑、维修均有不便。因此,不仅要求转盘轴承具有足够的强度和承载能力,而且要求其运行平稳、安全可靠,润滑、防腐及密封性能良好且寿命长。如果转盘轴承运行中产生故障,可能导致整个机械系统发生不可预知的故障,并带来巨大的经济损失[1]。综上所述,提取有效的故障特征对转盘轴承进行故障诊断意义重大。
目前,常用于转盘轴承故障诊断的方法有[2]:频谱分析、细化谱分析、解调谱分析、倒频谱分析、小波变换、小波包分析、第二代小波分析、希尔伯特-黄变换、基于多尺度主元分析的聚类经验模式分解法等[3]。其中时频分析法在近些年发展较快,其特点是能同时反映信号的时域和频域特征,有助于提高诊断精度。转盘轴承故障信号呈现一种非线性非平稳状态[4],故障信号中混有其他振源信号和噪声信号,传统时频域等故障诊断方法并不能对故障特征频率进行有效提取[5]。为此提出一种基于经验模态分解(Empirical Mode Decomposition ,EMD)和独立分量分析(Independent Component Analysis, ICA)盲源分离方法,不但解决了欠定盲分离中测试信号数量不足以及源信号数未知的问题,而且还提出了基于峭度的最优测试信号的选择标准,可以实现对故障信号的分离与诊断。
1 基于EMD和ICA的故障诊断原理
1.1 故障源分离方法的步骤
如图1所示,基于EMD和ICA盲源分离的步骤为:

图1 基于EMD和ICA盲源分离方法的流程图
1)通过EMD对单通道测试信号x(t)进行分解,得到其本征模态函数IMF,并将其组成多通道测试信号x=[x1(t),x2(t),…,xn(t)]T,其中x1(t),x2(t),…,xn(t)为测试信号x(t)的本征模态函数分量;
2)求出测试信号x的相关矩阵Rx=[x(t)x(t)H],并计算其相邻特征值的最大下降速比,对信号源数目进行估计;
3)利用峭度值,在测试信号x=[x1(t),x2(t),…,xn(t)]T中选出最优测试信号,令其信号数目与信号源数目相等;
4)将最优测试信号作为FastICA算法的输入,分离出故障源。
1.2 ICA盲源分离算法
盲源分离是近几年的研究热点,独立分量分析[6]更是其中的热点。ICA源于盲源分离,但又与其不同:ICA中所统计的信号是彼此统计独立的,而盲源分离中所统计的信号却未必是彼此统计独立的[7]。ICA数学模型如图2所示。

图2 ICA线性模型

(1)
用矩阵形式可表达为
x(t)=A·s(t)。
(2)
ICA的目标是求得一个分离矩阵W,从观测信号x(t)中分离出源信号s(t)。设ICA分离出的独立源信号为y(t)=[y1(t),y2(t),…yN(t)]T,则其分离过程为
y(t)=W·x(t)=W·A·s(t)。
(3)
其中,y(t)为源信号s(t)的近似估计,y1(t),y2(t),…,yN(t)相互独立,分离矩阵W的计算采用FastICA算法。
1.3 信源数的估计
由于实际生产应用中系统的机械结构复杂,导致其信源数一般都是未知的,而盲源分离的前提是准确估计信源数,因此需要对多通道测试信号进行信源数估计。由文献[7]可知,通过计算多通道测试信号x的相关矩阵Rx=[x(t)x(t)H]的优势特征值,可以估计信源数。通常优势特征值大于非优势特征值,并且对应系统的主要成分。因此,最大优势特征值与最小优势特征值间的优势特征值个数即为系统的信源数,相邻特征值之间最大下降速比为
n=1,…,N。
(4)
最大下降速比时λ的分子项即最小优势特征值,其下标即系统的信源数。
2 仿真验证
在转盘轴承上采集到的振动信号中通常有以下3种:转盘轴承的故障振动信号、齿轮啮合振动信号及液压马达工作振动信号。因此假定以下3个信号为振源信号
s1(t)=cos(2πf1t+10),
(5)
s2(t)=0.5cos(2πf2t-10),
(6)
s3(t)=sin(2πfbt)[1+αsin(2πfrt)],
(7)
其中,f1=20 Hz,f2=50 Hz,fr=10 Hz,fb=100 Hz,α=1.6,采样长度N=512。振源信号和噪声信号的时频域图如图3所示。

图3 仿真信号
在实际工程应用中,传感器所采集到的信号,是由转盘轴承振动信号、其他振源信号以及背景噪声信号混叠而成。为了模拟实际观测的混叠信号,先通过MATLAB随机产生混合矩阵A,

将源信号按照瞬时混叠模型x(t)=A·s(t)进行混叠,混叠合成后的时频域波形图如图4所示。

图4 混合信号
假定由于测试条件所限,传感器无法测得所有通道信号,只能得到其中1个通道的测试信号(即图4中的第1行信号x1(t))。为满足独立分量分析的条件,需要对x1(t)进行EMD分解构造多通道测试信号,结果如图5所示。

图5 x1(t)的EMD信号
x1(t)经EMD分解后得到8个IMF,其中最后1项为分解得到的趋势项,不包含故障信息,故将其舍去。将原混叠信号x1(t)与IMF1~IMF7组成新的多通道测试信号X,并计算其相关矩阵Rx=[x(t)x(t)H]的特征值,计算结果见表1。
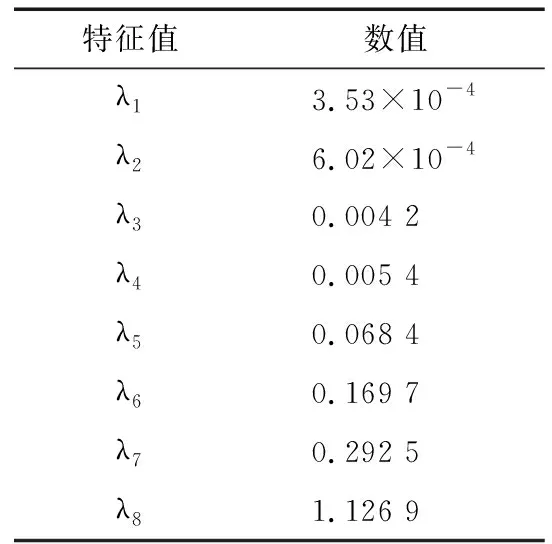
表1 相关矩阵Rx对应的特征值
相关矩阵Rx对应的特征值的下降速比如图6所示。
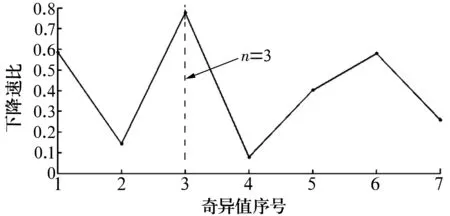
图6 相关矩阵Rx对应特征值的下降速比
由图可知,当n=3时,Rx对应的特征值下降速比取得最大值,即最大与最小优势特征值间特征值个数为3,信源数为3。因x1(t)含有大量故障信息,可作为最优测试信号的备选信号之一,另需从IMF1~IMF7中选出2个测试信号与x1(t)组成最优测试信号进行独立分量分析。因此,分别计算IMF1~IMF7的峭度值,结果见表2。

表2 仿真信号x1(t)分解信号对应的峭度值
由表可知,IMF4和IMF6对应的峭度值最大,因此,将IMF4和IMF6作为测试信号入选最优测试信号与x1(t)组成最优测试信号X,并将其作为独立分量分析FastICA的输入信号。分离出的故障源信号时域频域波形图如图7所示。
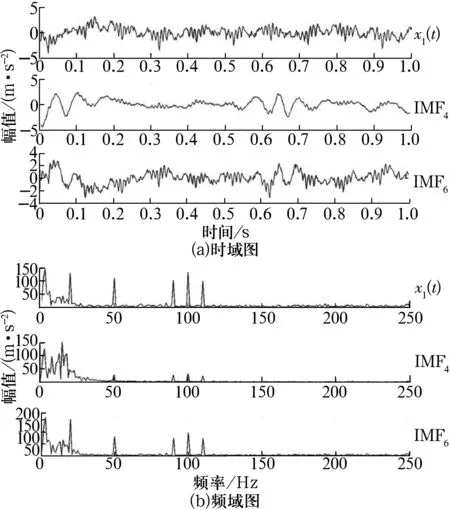
图7 最优测试信号盲源分离结果
测试信号经盲源分离后,其时域和频域波形与图3相比都有较大畸变,虽然故障源未能很好分离,但从其对应的频域波形中可以看出源信号的主要故障频率。而时域波形对诊断结果的影响不大,因此可以认为该方法能够有效地应用于转盘轴承的故障信号分离。
3 实际应用
3.1 试验方法
采用自主设计开发的风电转盘轴承试验台进行试验,该试验台可向转盘轴承施加轴向力及倾覆力矩,并通过液压马达驱动转盘轴承旋转,从而模拟转盘轴承的工作状况。转盘轴承试验台主要组成及信息流如图8所示,试验采用四点接触球转盘轴承QNA730,技术参数及主要试验参数见表3,故障特征频率[9]见表4。

图8 转盘轴承试验台主要组成及信息流

表3 转盘轴承技术参数及试验参数

表4 转盘轴承各部件故障特征频率
3.2 分析与故障诊断
如图9所示,在转盘轴承内圈上加工宽3 mm、深10 mm的长方形槽模拟内圈故障,采样频率为2 048 Hz,采样长度为6 144,转速为4 r/min。加速度传感器测得的时域波形如图10所示。

图9 缺陷示意图

图10 转盘轴承故障信号时域波形图
对采集到的转盘轴承加速度信号进行频谱分析,结果如图11所示,可以看到223,420.7,838.7 Hz处幅值较大;此频率接近齿轮啮合频率的高倍频。由于频谱中还含有其他振源信号并且含有大量噪声,导致故障信号的频线复杂,内圈故障基频不明显,无法从频谱图中直接判断故障位置。

图11 转盘轴承故障信号频谱图
由于转盘轴承故障信号集中在低频,为了获取故障特征明显的故障源,将图10中的故障信号进行低通滤波,滤除其高频成分,得到观测信号x1(t)。再将其信号进行EMD,以获得多通道测试信号,共得到7个IMF分量,其中IMF7为趋势项并不包含任何故障信息,故将其舍去。其余6个IMF分量对应时域波形图如图12所示。

图12 单通道测试信号x1(t)的EMD结果
x1(t)经EMD后得到6个包含有故障信息的IMF分量,将信号x1(t)与6个IMF分量组成新的多通道测试信号x=[x1(t),x2(t),…,x7(t)]T。计算x的相关矩阵Rx=[x(t)x(t)H]的特征值以估计信源数,计算结果见表5。

表5 相关矩阵Rx对应的特征值
相关矩阵Rx的特征值下降速比如图13所示。由图可知,相关矩阵Rx特征值的下降速比在n=3时达到最大值,即最大与最小优势特征值之间特征值的个数为3,因此可以确定信源数为3。

图13 相关矩阵Rx的特征值下降速比
x1(t)可作为入选的最优测试信号的信号之一,因为x1(t)含有大量故障信息。分别计算余下的IMF1~IMF6的峭度值,结果见表6。
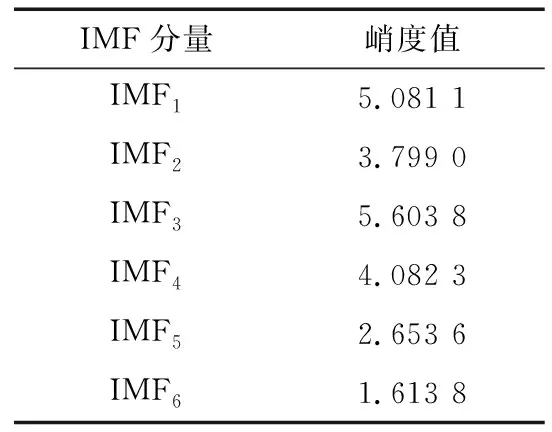
表6 x1(t)各分量峭度值
从表6中可以看出IMF1,IMF3的峭度较大,因此可以作为最优测试信号,与x1(t)组成最优测试信号[x1(t);IMF1;IMF3]输入FastICA。将最优测试信号输入FastICA算法,得到分离矩阵W,进而分离出源信号。得到源信号的时域波形图如图14所示。
对图14中的信号分别作功率谱分析,其中故障峰值最明显的IMF1分离信号的功率谱如图15所示。

图14 分离出故障源的时域波形图
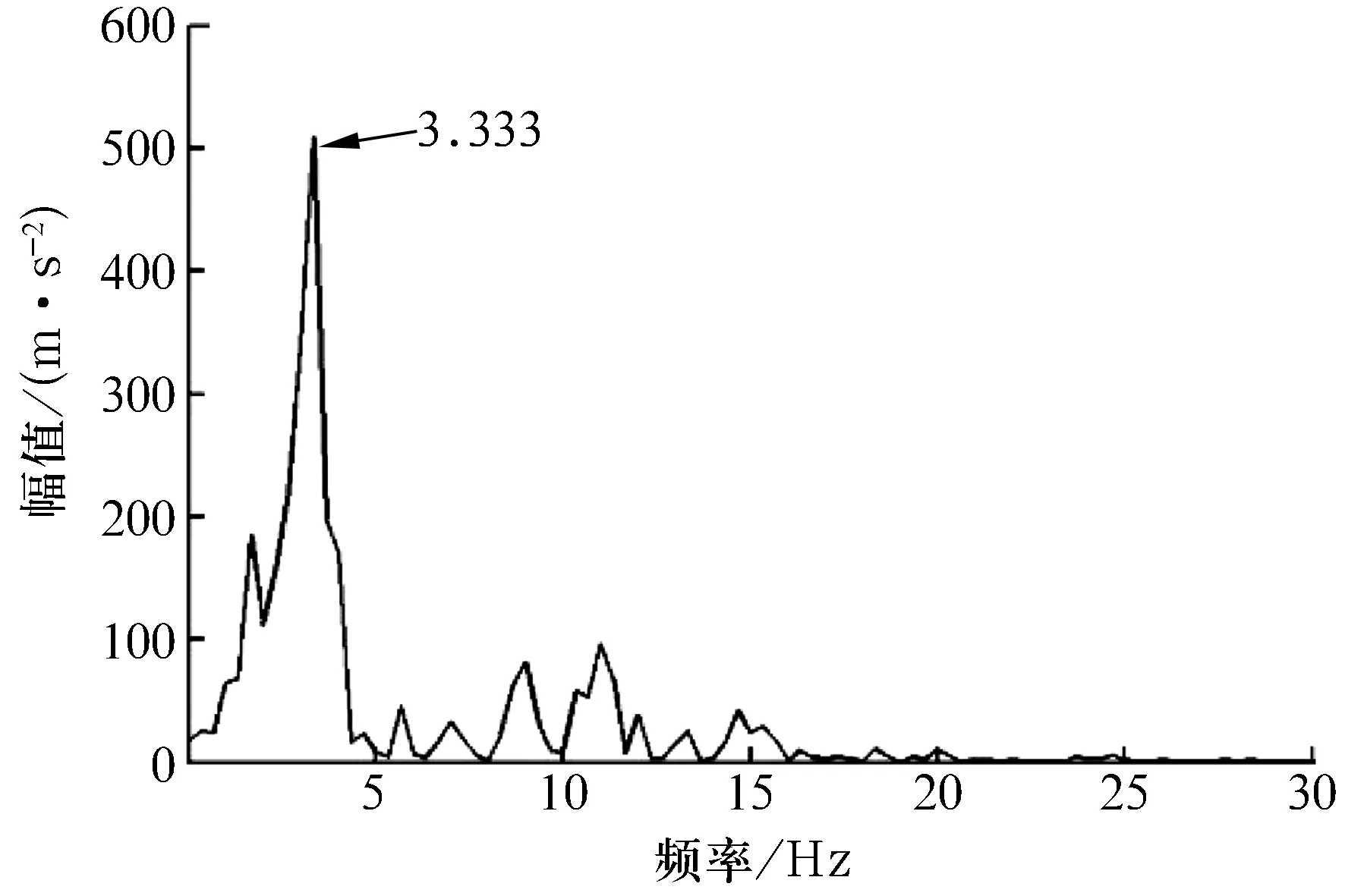
图15 故障源功率谱
由于转盘轴承内圈故障特征频率为3.28 Hz,这与图15故障源功率谱中所提取到的3.333 Hz最为接近,所以基于EMD和独立分量分析的盲源分离方法在转盘轴承故障诊断中是有效的。
4 结束语
在传统机械故障诊断过程中,由于工业现场工作环境复杂、背景噪声大等,很难对机械故障特征频率进行有效地提取[10]。尤其对于转盘轴承类机械部件,与一般轴承相比,转盘轴承的故障特征频率更低,更加容易淹没在背景噪声中。利用EMD和独立分量分析方法可以有效地从背景噪声中分离出故障信号,并提取故障特征信号,同时利用EMD方法有效解决了盲源分离中测试信号通道数不足的问题,为欠定盲分离提供一种有效的解决方法。
