凸度滚子轮廓的比较测量
2015-08-01嵇文超陈晓阳陆锦才余剑葛德成
嵇文超,陈晓阳,陆锦才,余剑,葛德成
(1.上海大学 轴承研究室,上海 200072;2.上海和锦滚子科技有限公司,上海 201600)
对于常见的触针式轮廓仪,测量前需精确调整机械平台,锥度的存在会影响圆柱滚子凸度量测量的精确性,另外,尚没有实现被测滚子轮廓与理论设计轮廓吻合度的直接图形比较[1]。
为此,在原有触针式轮廓仪机械架构的基础上,引入数字式数据测控技术,形成高精度、高可靠、控制灵活方便的下位机测控电路;并运用VB编程,研制出一套界面友好、操作方便、功能强大、运行可靠快捷的上位机智能化软件系统。该系统实现了实时数据的采集和可视化,经过标度变换和数值标定后以图形形式直观显示原先的电感测量值,并根据滚子状态旋转一定角度,同时计算出实际的凸度量。还可根据凸度量设计公差画出公差范围,根据实测曲线是否落在公差范围内判别滚子形状是否合格。
1 滚子轮廓仪
1.1 测量原理
滚子轮廓如图1所示,图中,Cr为滚子倒角半径,Td为滚子跌落量。根据企业标准,定义距离端面1.2倍倒角处半径方向上的跌落量为凸度量。

图1 滚子轮廓示意图
测量原理如图2所示,工作台可以平移,传感器触头随滚子轮廓上下移动造成电感变化,电感测试仪实时显示电感量,并通过RS232接口将其传输到电脑,经标度变换后以μm为单位输出并以曲线的形式实时画出,最后在电脑上显示并打印[2]。

图2 测量原理图
1.2 信号测量方式
TH2775B型高精度电感测试仪能够自动测量电感量L、电阻值R、品质因素Q,提供了RS232接口,可有效实现与计算机的通信,并提供远程控制及数据采集。
测量过程中,为达到实时和直观显示的目的,一般将被测件半径方向的位移量放大5 000倍(可自己选择或输入放大倍数,2 000~10 000),通过测杆使磁芯与线圈的相对位置发生改变,从而使线圈的电感量发生变化。与传感器配套的电气部分将变化信号进行放大、整形处理后,通过A/D转换以数字信号的形式显示电感量,并通过RS232通信接口发送至计算机(图3)。

图3 测量电路框图
被测件沿轴线方向(即传感器水平移动方向)的位移固定放大10倍,通过工作台匀速平移速度(0.5 mm/s)乘以时间获得。工作台旁边有固定标尺,触针从距离端面1.2倍倒角处开始测量,但此前是工作台移动,而触针不动。
1.3 电感量测量方法
为提高电感量测量精度,采用开尔文4线检测方法,以减小引线及连接点对测试结果的影响(尤其是损耗),特别是在对低阻抗元件进行检测时,将驱动端和检测端分开连接至元件的引线端,消除了布线和接触电阻的阻抗。在此有专门的4端测试电缆,分别为HD,LD,HS和LS,检测方式如图4所示。

图4 测试电缆示意图
1.4 标度变换
采样数据为模拟量电压,通过A/D转换电路在数码管上显示电感量,并经过标度变换反映表面微观几何数值。
DGC-6PG/A差动电感式位移传感器属于旁向式位移测量头,磁套内布置有1个初级线圈,初级线圈左右各布置1个次级线圈,呈对称分布。其等效电路如图5所示[3]。

图5 等效电路
由图5可得[3]
(1)
式中:r,u0,W和l均为与线圈结构和材料有关的常数。将已知参数看为常数,(1)式可简化为L2=kx+b,则ΔL2=kΔx,可知ΔL2与Δx成线性关系。所以用电感测试仪测出电感量L,然后再用量块标定的方法得出k并用其表示微观几何数值是可行的。
设传感器的传递系数为k,表面微观几何数值为Y,传感器电感量值为Y0,则
Y=Y0/k。
(2)
1.5 考虑偏斜度的峰谷幅值参数算法
以峰值和谷值定义的评定参数有:最大轮廓峰高、最大轮廓谷深、最大轮廓高度、微观不平度的十点高度、轮廓单元的平均线高度、轮廓的总高度等。在此,选用最大轮廓高度Rz,即评定长度内最大轮廓峰高Zp与最大轮廓谷深Zv之和。如图6所示,设表面轮廓数据存在数组y[i]中,数组长度为N,则最大轮廓高度[3]为
Rz=max{y[i]}+|min{y[i]}|;i=0,1,…,N。
(3)

图6 轮廓最大高度
参照理论曲线旋转实测曲线,并根据需要调节到相应的角度,设偏斜角为α,则
Rz=max{y[i]}+|min{y[i]} |cosα;i=0,1,…,N。
(4)
1.6 考虑失真的曲线旋转算法
在粗糙度轮廓仪上,一般需要将被测件放在V形架上机械调平后进行测量,由于手工很难精确调节,导致存在一定的测量误差。因此,对曲线进行测量后的旋转以达到需要的精度,即用软件调平取代机械调平。
由于滚子凸度为微米级,一般将纵坐标放大2 000~5 000倍,难点是如何在纵坐标放大k倍的状态下围绕某点进行不失真的坐标旋转。假设点(x,y)绕基点(x0,y0)逆时针旋转角度α后变为(x′,y′),则在横坐标恒比例的情况下,推导出的旋转公式为[5]
(5)
注意:在本程序中,所有基点 (x0,y0)均为曲线的左端点,即所采集数据的第1点。
1.7 操作界面及流程
操作界面如图7所示,采用框架划分工作区域,操作顺序遵循从左到右,从上到下的原则。被测滚子轴线方向测量范围为20 mm,放大倍数为10,其数值变化与测量时间相匹配。半径方向测量范围为20 μm,放大倍数可通过软件平台任意选取。电动机速度恒定,以双刀三位开关控制其正反转停。数据采集设计为人机一体界面,自动采集轮廓原始数据。操作流程如图8所示。

图7 操作界面
2 轮廓形状误差的在线比较
根据Lundberg对数曲线的凸度量设计[5-6],在不考虑越程槽等因素的情况下,滚子表面形状可表示为

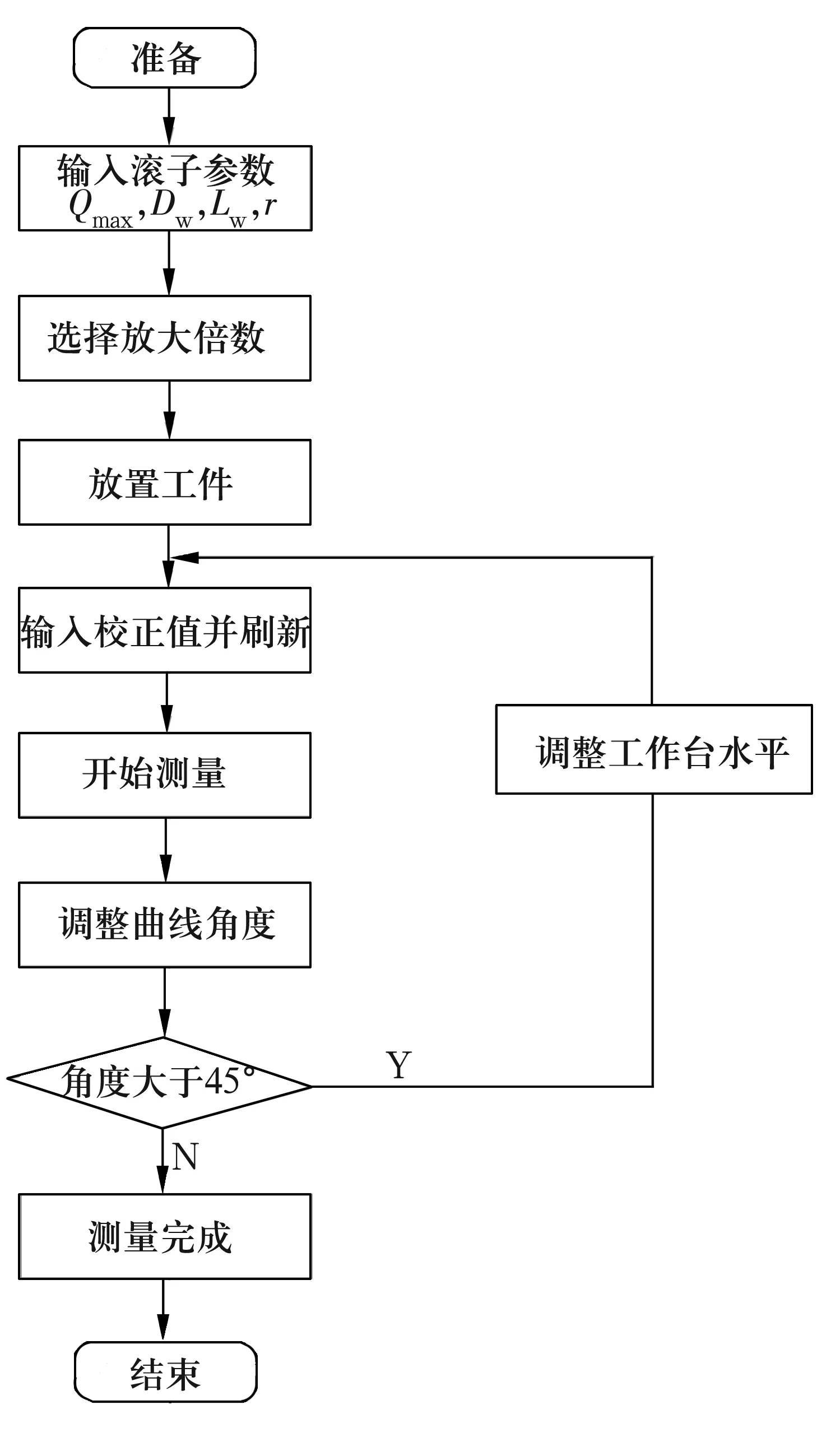
图8 操作流程图
式中:Q0为单个滚子承受的最大载荷,N;Lwe为滚子的有效接触长度,mm;Dw为滚子直径,mm;E1与E2分别为滚子与滚道材料的弹性模量;ν1与ν2分别为滚子与滚道材料的泊松比。轴承钢的弹性模量为E=208 GPa,泊松比为ν=0.3。
根据企业标准,查滚子形状误差表得:当II级滚子的Dw≤18 mm时,形状误差ΔTd≤2 μm。因此,在线比较的时候引入公差范围,虚线为实测线(无需精确调整工作台),2条实线为理论曲线的上下偏差,只要虚线大部分落入实线所包含的区域,即可判断实测滚子的轮廓形状与设计轮廓符合。
在此,测量经超精加工的φ12 mm×14 mm的圆柱滚子,结果如图9所示。

图9 对数滚子凸度量测量结果
3 对比分析
3.1 测量准确性
对于同一个φ12 mm×14 mm的圆柱滚子,采用KosaKa SE-40H粗糙度轮廓仪测量的凸度量Rmax为4.9 μm。而所研发轮廓仪第1次凸度量的测量结果为4.4 μm,分析认为:由于人为误差,导致滚子素线不可能完全调平,且调平过程中没有基准线作参考,所以实际的Rmax并没有KosaKa SE-40H粗糙度轮廓仪测量的大。
3.2 重复性精度

4 结束语
在分析二维触针式轮廓仪测量原理的基础上,设计了数字式数据测控系统,其优点为:1)用软件调平取代了手工机械调平滚子素线,排除了人为因素的测量误差;2)测量前输入基本参数即可得到理论曲线,并在测量后反映调整状态,读出旋转角度;3)加入了合格公差范围,很容易辨别实测滚子的形状是否符合工程要求;4)考虑了素线不可能精确调平情况,运用旋转公式实时计算出凸度量。
经实际应用表明,测量相对误差为6.5%,重复性误差为1.6%,完全能够满足产品检测的精度要求。
