圆锥滚子贯穿式无心磨削锥面廓形直线性分析

高作斌，张建奇，张贝，毕晓磊

(1．河南科技大学 机电工程学院，河南 洛阳 471003；2．洛阳LYC轴承有限公司 滚子厂，河南 洛阳 471003)

圆锥滚子是滚动轴承中的关键零件，其加工质量成为制约我国高端轴承制造的瓶颈之一[1]。

锥面的贯穿式无心磨削是圆锥滚子加工中的一道主要工序[2]，常出现滚子锥面廓形内凹现象，影响产品质量。如果后续没有超精研工序，磨削后廓形内凹的滚子用于轴承时将加大滚子与滚道之间的边缘应力效应，影响轴承寿命；如果后续有超精研工序，磨削后廓形内凹将加大滚子超精研难度，影响超精研质量和效率。

滚子锥面廓形内凹较严重时通常按照直线性不合格对待，但是，有些圆锥滚子对轮廓直线性提出高要求并不仅仅是为了避免轮廓内凹。比如，高精度圆锥滚子的贯穿式无心磨削对锥面廓形直线性工艺要求较高，主要有以下几方面考虑：1)为后续的超精研工序提供良好的轮廓形状基础；2)为了保证滚子的圆度和波纹度，因为这种磨削方式中，滚子锥面既是加工面同时也是定位面，其廓形直线性误差会影响导轮及刀板对滚子支承和定位的稳定性，从而影响滚子的圆度和波纹度；3)某些强调高旋转精度的轴承，对滚子并不希望有凸度，只要求有高直线性。

对圆锥滚子贯穿式无心磨削的锥面轮廓形状问题已经开展了一些研究，但对相关问题的认识仍然不够深入。研究多关注滚子轮廓凸度[3-5]和导轮[5-6]，对轮廓直线性和刀板关注较少。在圆锥滚子贯穿式无心磨削中，滚子与砂轮之间的关系是决定滚子锥面廓形的重要因素，其中，滚子与砂轮之间的几何关系不仅受导轮影响，也受刀板影响。将砂轮修整成直廓圆柱形，使滚子沿着与砂轮轴线平行的直线贯穿，是一种常用的贯穿式无心磨削方法，基于此，重点从分析圆锥滚子与砂轮和刀板之间的几何及运动关系着手，依据机械加工表面形状形成的基本原理，探究锥面直线廓形的形成条件，以及实际的滚子-砂轮几何关系，并对影响滚子廓形直线性的因素进行分析。

1 圆锥滚子贯穿式无心磨削方式

圆锥滚子贯穿式无心磨削的加工方式如图1所示。砂轮和导轮做定轴转动；圆锥滚子由导轮和刀板共同支承，在导轮和砂轮共同驱动下，一边自转一边贯穿通过砂轮磨削区。砂轮轴线沿水平纵向布置，不能调整；导轮轴线总体沿水平纵向布置，其轴线在水平和铅垂面内可以有小范围的调整，因此，磨削时导轮轴线与砂轮轴线之间既可以保持平行，也可以保持轻微的空间交错或平面相交几何关系。磨削时，滚子自转运动由砂轮对滚子的切向磨削力与导轮和刀板对滚子的切向摩擦力合成产生，滚子自转速度由导轮控制；滚子贯穿运动由导轮挡边推动，其贯穿速度由导轮控制；滚子姿态由导轮螺旋工作面廓形与刀板共同决定；滚子贯穿运动的轨迹由导轮轴线方向、导轮螺旋工作面直径沿其轴向的变动情况以及刀板的方位共同决定。

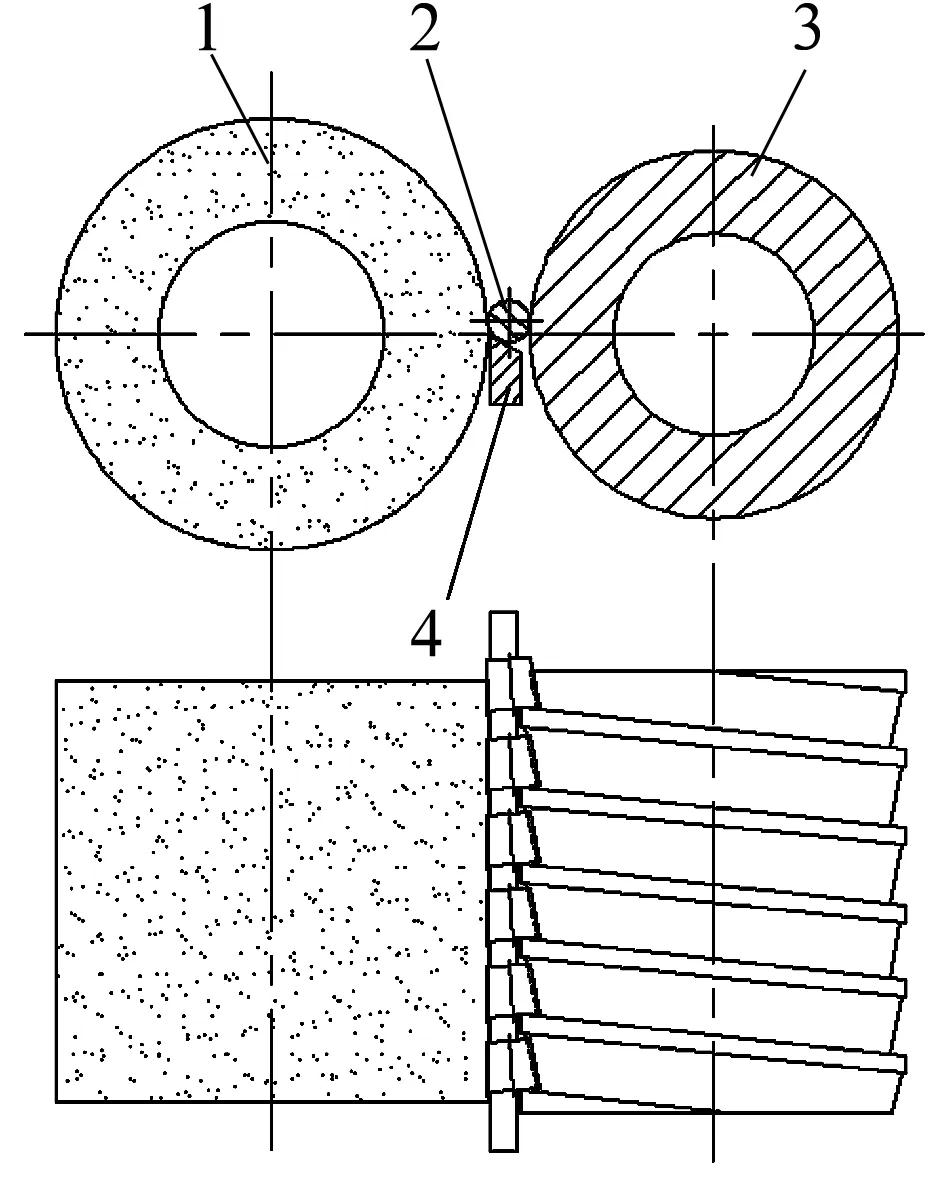
1—砂轮；2—圆锥滚子；3—导轮；4—刀板图1 圆锥滚子贯穿式无心磨削示意图

2 理想滚子-砂轮关系

依据机械加工表面形状形成的基本原理，只要滚子与砂轮之间满足一定的几何及相对运动关系，理论上，圆锥滚子贯穿式无心磨削可以在保证锥角的同时获得锥面直线廓形。理想的滚子-砂轮关系是：砂轮修整为直廓圆柱面；滚子沿直线贯穿；滚子轴线、滚子中心贯穿直线以及砂轮轴线三线共面；滚子轴线与砂轮轴线相交且交角等于滚子半锥角；滚子中心贯穿直线与砂轮轴线平行。

基于圆锥滚子贯穿式无心磨削，由于滚子中心高的存在，获得直线廓形时理想的滚子-砂轮关系如图2所示。图2中，O1为砂轮转动中心；O2为导轮转动中心；O为圆锥滚子大端圆心；O点到O1O2的距离为滚子中心高；砂轮轴心线以及O1和O2的连线均处于水平面，而O1和O的连线相对于水平面倾斜γs角(滚子与砂轮的接触角)；A-A平面为过砂轮轴线以及O1和O连线的平面；A-A平面内砂轮的直素线与砂轮轴线平行(砂轮为直廓圆柱面)。滚子与砂轮之间的关系为：滚子轴线与砂轮轴线共处于A-A平面内且相交，其夹角为滚子半锥角α；滚子中心贯穿直线也处于A-A平面内，且与砂轮轴线平行，从而保证该平面内滚子直素线与砂轮直素线始终重合于同一直线。

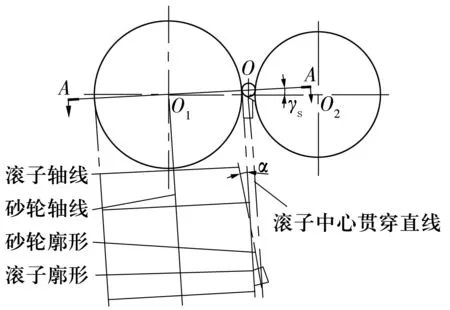
图2 获得直廓形时理想滚子-砂轮几何关系示意图

3 实际滚子-砂轮关系

理想的滚子-砂轮关系对滚子姿态和贯穿运动轨迹提出了特殊要求，然而，滚子姿态和贯穿运动轨迹是由导轮和刀板控制的，因此，实际滚子与砂轮之间的关系由滚子与导轮和刀板之间的关系来保证。滚子贯穿运动轨迹分为直线和曲线两类，这里仅针对滚子沿着与砂轮轴线平行的直线贯穿，且将砂轮修整成直廓圆柱形的磨削方法，从滚子与刀板之间的关系着手，分析实际滚子-砂轮的关系。

3.1 理想滚子-砂轮关系的实现条件

刀板与滚子接触的表面是一个固定不动的斜面。滚子与刀板之间相对运动关系是一种滚滑关系。滚子与刀板之间的接触几何关系为直线接触，接触直线的方位可以通过导轮及刀板角度进行调整。滚子与刀板的接触直线必定是滚子的一条素线，其与滚子轴线之间有确定的几何关系，滚子轴线的方位确定后，接触直线的方位也确定，因而滚子与刀板的关系问题可以归结为滚子轴线的方位问题。

上述理想滚子-砂轮关系下，滚子轴线的方位是确定的，但在这种方位下滚子与刀板是否能保持直线接触，尚待确定。反之，在滚子与刀板保持直线接触的条件下，滚子轴线调整到理想滚子-砂轮关系所需要的方位、实现条件，尚待分析。

由图3可知，当滚子大端直径、小端直径或滚子锥角等几何参数变化时，滚子大、小端圆心位置随之变化，从而使滚子轴线方位发生变动；当更换不同倾斜角度的刀板时，滚子轴线方位也会变动；此外，即使滚子几何参数和刀板倾斜角度都不变，滚子轴线方位也会伴随不同的导轮廓形或导轮轴线方位而变动，但这种情形下滚子小端圆心只能在F-F平面上变动(考虑到滚子轴线方位取决于滚子小端与大端圆心的相对位置，这里假定滚子大端圆心不动)。因此，在滚子与刀板保持直线接触的条件下，滚子轴线方位有很大调整余地。

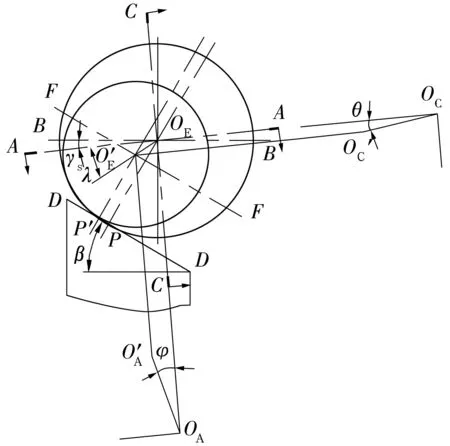
图3 滚子与刀板保持直线接触时滚子轴线方位示意图

考察第1种典型的滚子轴线方位，即滚子轴线处于A-A平面内(图4)。图4中与图3相比位置发生变动的点，其符号增加下标“1”；φ1对应图3中的φ；原图3中的λ和θ在图4中已不存在(其值均变为0)。

图4 第1种典型滚子轴线方位示意图

由图4可知

(1)

(2)

(3)

滚子-刀板接触线PP′是滚子的一条素线，与滚子轴线共面，在该平面内，表示滚子大、小端圆心到刀板斜面距离的线段OP和O′P′与滚子几何参数之间的关系如图5所示。图5中，滚子大端半径为R，小端半径为r，长度为l，半锥角为α。

由图5可知

OP=Rcosα，

(4)

O′P′=rcosα，

(5)

R-r=ltanα。

(6)

图5 滚子大、小端圆心到刀板斜面距离与滚子几何参数之间关系示意图

OP-O′P′=lsinα。

(7)

注意到：(2)式中的OEP1-O′E1P′1与(7)式中的OP-O′P′都表示滚子大端和小端圆心到刀板斜面的距离之差，因而两者相等；(1)式中的OA1O′A1是滚子轴线所在A-A平面内表达的滚子大小端中心距，其长度即为l。因此，将(3)式代入(2)式整理后，再代入(1)式可得

(8)

滚子轴线方位要满足上述理想滚子-砂轮关系要求， (8)式中φ1值应满足φ1=α，从而得出理想滚子-砂轮关系的实现条件为γs+β=90°。

3.2 实际滚子-砂轮关系

由于砂轮和导轮直径大，而滚子直径小，中心高很小，因而γs的值很小(一般只有1°～3°)；另一方面，刀板斜面倾斜角β的取值受空间和自身刚度的限制，一般也不超过60°，因此，γs+β=90°实际中无法满足，这就表明，理想滚子-砂轮关系是无法实现的。

圆锥滚子磨削中，除了有锥面廓形直线性要求外，还必须保证滚子的锥角。图4所示的典型滚子轴线方位可以获得理想直线廓形，但由(8)式可知，φ1≥α，这意味着磨削后滚子的锥角将增大，因此，第1种典型滚子轴线方位及其对应的滚子-砂轮关系不能用于实际加工。

考察第2种典型滚子轴线方位，即滚子轴线不在A-A平面，但其在A-A平面的投影与砂轮轴线的夹角仍为滚子半锥角α(为了保证磨削后滚子锥角不变)。这种典型滚子轴线方位如图6所示，图6中与图3相比位置发生变动的点，其符号增加下标“2”；α对应图3中的φ；θ2对应θ；λ2对应λ。

如前所述，越裔导演站在西方视角以追忆和人道主义同情的姿态完成了形式上的现实主义叙事；本土导演基于个人关于本土的切身体验，冷静专注地再现了挣扎在现实生活流中的个体，达到一种现实主义主题上的深刻。二者的共生共存对越南电影发展的整体影响是，一方面极易造成域外观众对越南的某些刻板认知，另一方面体现了当前越南电影发展路径的多元化。

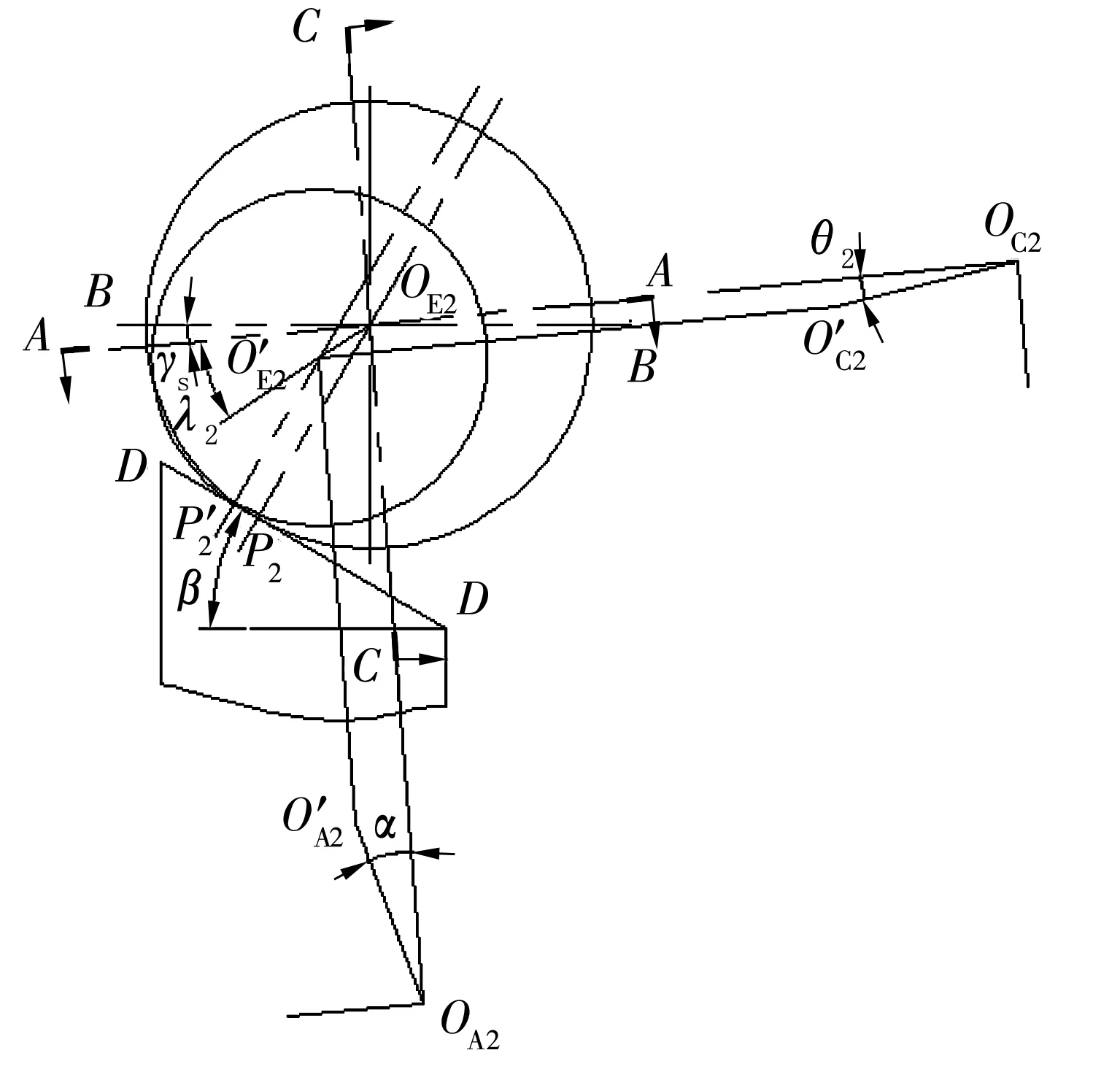
图6 第2种典型滚子轴线方位示意图

由图6可知

(9)

∠O′E2OE2P2=90°-(γs+λ2+β)。

(10)

对于给定的滚子几何参数，滚子轴线方位变动时，滚子大、小端圆心到刀板斜面的距离保持不变，故有

OE2P2=OE1P1,

(11)

(12)

将(5)～(7)式代入(11)，(12)式整理，再将(10)～(12)式代入(9)式可得

(13)

图6所示的第2种典型滚子轴线方位中，滚子轴线与其在A-A，C-C和横截面E-E上投影的空间几何关系如图7所示。图中，O和O′分别为滚子大、小端圆心，其距离为滚子长度l。

图7 第2种典型滚子轴线方位的空间几何关系示意图

由图7可知

OOA2=lsinλ3=lcosα3sinλ2，

(14)

O′O′E2=lsinα3=lcosλ3sinα2，

(15)

OE2O′E2=lcosα3，

(16)

α2=90°-α。

(17)

整理(15)，(16)式可得

(18)

(19)

将(17)，(18)式代入(16)式可得

(20)

对比(13)和(20)式可知

(21)

可进一步改写为

sin2(λ2+γs+β)+(cosαsinλ2)2=1。(22)

由(22)式求解λ2可得

(23)

a=sin4α+4cos2αcos2(γs+β)；

b=-(1+cos2α)cos2(γs+β)；

c=cos4(γs+β)。

由图7还可以看出

(24)

将(17)～(19)式代入(23)式可得

tanθ2=tanαtanλ2。

(25)

对于第2种典型滚子轴线方位，当已知α时，可分别由(23)和(25)式求出λ2和θ2。实例计算：已知α=2°，β=30°，γs=1.5°，由(23)式计算得λ2=29°15′34″；由(25)式计算得θ2=1°7′15″。

由图6可以看出，第2种典型滚子轴线方位下滚子轴线与砂轮轴线处于空间交错状态，这将导致磨削后滚子的锥面廓形存在直线性偏差，即锥面廓形是内凹的，而且空间交错角越大，内凹越严重。对这种内凹廓形产生机理的一种简单的理解是：一条直线绕另一条与其空间交错的轴线旋转后会形成双曲面，交错角越大，该双曲面轴向截形的内凹程度越严重。滚子轴线与砂轮轴线的空间交错角即图6和图7中的滚子轴线方位角θ2。计算实例表明，θ2的值相当小，因此滚子磨削后锥面轮廓形状内凹程度也比较小。

鉴于第2种典型滚子轴线方位可以保证磨削后滚子的锥角不变，而其引起的滚子锥面廓形内凹程度较小，作为一种近似加工方法，这种滚子轴线方位可以用于圆锥滚子锥面磨削，其滚子-砂轮关系也是一种实际的滚子-砂轮关系。

4 滚子锥面廓形直线性的影响因素

上述分析表明，在圆锥滚子贯穿式无心磨削中，将砂轮修整成直廓圆柱形，并使滚子沿着与砂轮轴线平行的直线贯穿，要保证磨削后滚子锥角不变，理论上滚子锥面廓形是内凹的。因此，这种加工方法用于对锥面廓形直线性要求比较高的圆锥滚子磨削时，需要充分了解影响廓形直线性的因素并进行严格控制，才能保证磨削后滚子的形状精度要求。

基于滚子锥面内凹廓形的产生机理，空间交错角θ2是廓形内凹程度的决定性因素，θ2越大，内凹越严重，因此，通过分析影响θ2的相关因素来判断对滚子锥面廓形直线性的影响。

4.1 滚子半锥角α

由(25)式可知，α增大会直接导致θ2增大；由(22)式可知，当α增大时，λ2也将增大，继而间接导致θ2增大。表明大锥角滚子磨削后的锥面廓形内凹程度比小锥角滚子严重。

4.2 刀板斜面倾斜角度β

由(22)式可知，当β增大时，λ2将减小，继而导致θ2减小。表明增大刀板倾斜角度有利于提高滚子锥面廓形直线性。

4.3 滚子与砂轮的接触角γs

由(22)式可知，当γs增大时，λ2将减小，继而导致θ2减小。表明增大γs有利于提高滚子廓形直线性。需要注意的是，实际的γs变化范围很小，γs的选择还要考虑其对滚子成圆过程的影响，因而其对滚子锥面廓形直线性的提高不会起到太大作用。

需要说明的是，采用非直线廓形的砂轮，以及通过调整导轮或特殊制作导轮使滚子沿曲线贯穿等，也会影响滚子锥面廓形的直线性，其影响机制与规律更加复杂，有待另文阐述。

5 结论

1)在圆锥滚子贯穿式无心磨削中，将砂轮修整成直廓圆柱形，并使滚子沿着与砂轮轴线平行的直线贯穿是一种近似磨削方法。用这种方法加工，在保证滚子锥角不变的条件下，理论上存在滚子锥面廓形直线性偏差，滚子锥面廓形是内凹的。

2)滚子轴线与砂轮轴线之间存在空间交错角是产生滚子廓形直线性偏差的根本原因，该交错角可由(23)和(25)式进行计算。

3)滚子半锥角越大，锥面廓形直线性偏差越大；刀板斜面对水平面倾斜角度越大，锥面廓形直线性偏差越小。