基于多体动力学的扭转梁半独立悬架优化设计

康小鹏，汤爱华

(1.成都大学 机械工程学院，四川 成都 610106;2.北京理工大学 机械与车辆学院，北京 100081)

0 引 言

近年来，随着计算机技术及基础理论的不断发展和进步，多体动力学已越来越多地应用在汽车设计的各个领域.在汽车悬架系统设计中，一个数字化悬架模型往往需要考虑由于大位移、旋转位移以及非线性力引起的非线性效应，而刚体系统并不能完全反映所有构件的性能.在扭转梁式半独立悬架中，扭转梁通过扭转变形，对车轮垂直运动起到了解耦作用，车轮跳动以及施加载荷会引起扭转梁的弹性变形，这种变形将影响到悬架运动学特性的变化［1］.由于弹性变形对悬架运动学特性将产生影响，仅利用传统的建模方法来对其分析势必对仿真结果的准确性有较大影响.对此，本研究基于多刚体动力学非线性方法，利用ADAMS/Car 建立了扭转梁式半独立后悬架模型，对其进行运动学仿真分析，并利用ADAMS/Insight 进行优化设计.

1 多体动力学与ADAMS 理论

通常，对于受约束的多体系统，其动力学方程是先根据牛顿定理，给出自由物体的变分运动方程，再运用拉格朗日乘子定理，导出基于约束的多体系统动力学方程.ADAMS 是一款基于多体动力学理论开发的机械系统多体动力学仿真设计软件，它以质心笛卡尔坐标和反映刚体方位的欧拉角作为广义坐标，采用拉格朗日乘子法建立系统运动方程:

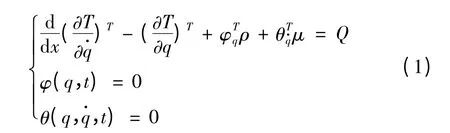
式中，T 为系统动能，q 为系统广义坐标列阵，Q为广义力列阵，ρ 为对应于完整约束的拉氏乘子列阵，μ 为对应于非完整约束的拉氏乘子列阵.在ADAMS 软件中，运动学分析主要研究零自由度系统的位置、速度、加速度和约束反力，因此只需求解系统约束方程［2］，

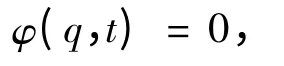
即可.

2 扭转梁后悬架模型

扭转梁式半独立悬架一般作为后悬架运用于发动机前置的前驱乘用车，其主要优点是结构紧凑，制造简单，空间利用率较高，容易实现后轮随动转向功能.扭转梁悬架的实体模型如图1 所示.

图1 扭转梁悬架模型示意图

为了便于建模和分析，本研究对其结构进行适当简化后的拓扑结构如图2 所示.当车轮上下跳动时，纵臂以套管的轴线为中心摆动，使扭杆弹簧产生扭转变形，以缓解路面不平产生的冲击力［3］.由于扭转梁的柔性结构，其在悬架运动过程中左右稳定杆回转中心轴线不一致，使得悬架同时产生弯曲和扭转变形，加上弹簧、减振器、隔振垫块等非线性因素，用传统的建模和求解方法难以对其进行准确地运动学分析.

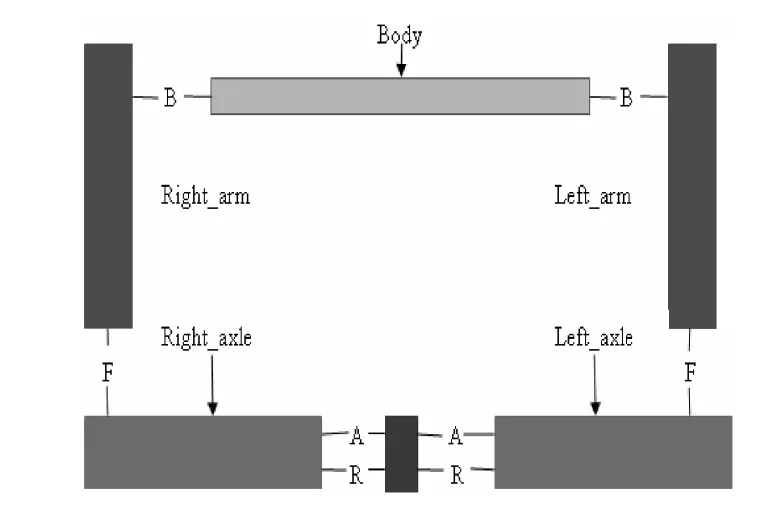
图2 悬架拓扑结构示意图

在ADAMS 中，可以利用节点力执行器来定义2部件之间的平移或者是扭转的单矢量(分量)力，且通常有3 种连接类型:转动连接、移动连接、柱连接.为了更准确地描述扭转梁的柔性特质，本研究采用ADAMS 提供的另外一种定义柔性体的方法，直接导入有限元分析软件生成的mnf 文件，并在此基础上建立悬架的其他部件，如拖曳臂、稳定杆、橡胶衬套，最后构建悬架运动学分析试验台，这些试验台包含了向车轮轮心指派垂直位移和施加载荷的命令［4］.在ADAMS/Car 中建立的扭转梁半独立悬架仿真实验台如图3 所示.

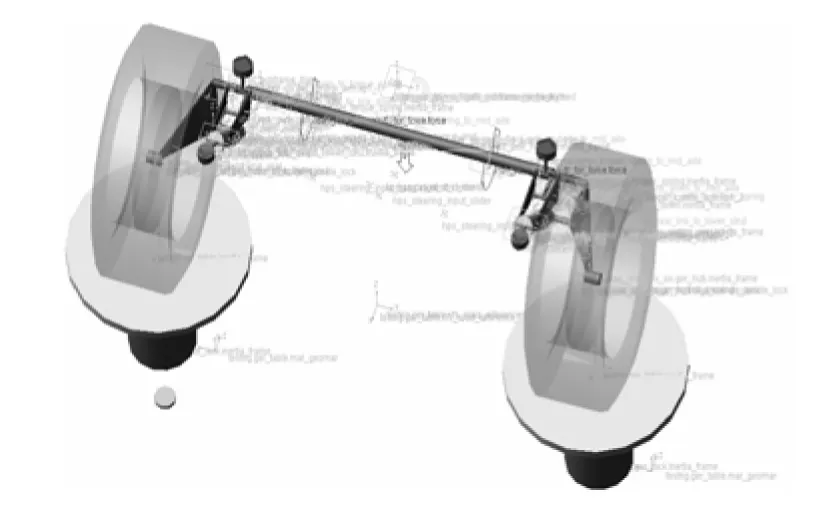
图3 悬架仿真实验台示意图

3 悬架运动学分析

汽车悬架在车轮跳动过程中其定位参数发生变化称为悬架运动学特性.在研究悬架运动学特性时，常采用车轮同向跳动激励仿真分析方法，通过仿真计算可以得到悬架主要运动学参数:前束角及车轮外倾角变化.在本研究中，仿真参数设置为，选择车轮同向跳动，施加激励大小为正负各100 mm，对悬架进行运动学仿真分析，其前束角和车轮外倾角随车轮垂向位移变化曲线如图4、5 所示.

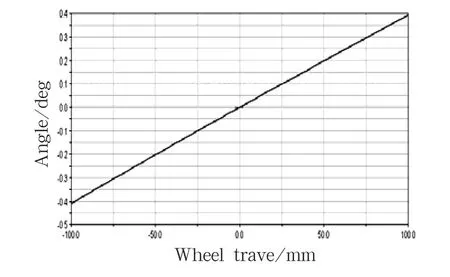
图4 左车轮前束角变化曲线

图4 为前束角随车轮跳动激励下的变化曲线.车轮上跳及回落时的前束变化对汽车直行稳定性与汽车的稳态响应特性(不足转向及过多转向)有很大的影响，是汽车悬架的重要设计参数之一.通常，前束比较理想的设计特性是变化在(－1° ～1°)/100 mm 范围内［5］.当汽车行驶时，前束变化过大将会对汽车直线行驶稳定性不利，同时增大轮胎与地面间的滚动阻力，加剧轮胎的磨损.所以，前束角的设计原则是，在车轮跳动时，前束角变化尽可能的小.由图4 可知，车轮前束角的变化幅度偏大，可以适当进行优化.

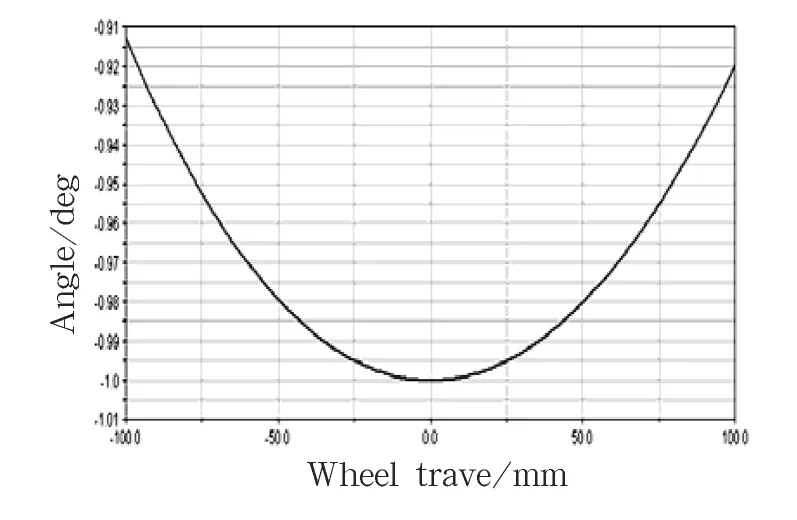
图5 左车轮外倾角变化曲线

图5 为车轮外倾角随车轮跳动激励下变化曲线.车轮跳动时外倾角变化对汽车的稳态响应特性等有着很大影响，从减小轮胎磨损以及改善操纵稳定性方面考虑，应尽量减少车轮相对车身跳动时的外倾角变化.为防止车轮出现过大的不足转向或过度转向趋势，一般希望车轮外倾角变化在一个很小的范围.通常情况下，当汽车在满载工况时，车轮上下跳动100 mm 时，外倾角的变化范围为:－3.1° ～1.3°，车轮外倾角的变化最好不超过±1°.图5 所示车轮上下跳动100 mm 时，外倾角变化［6］为－1.0°～－0.913°，这与预期的要求一致，满足设计要求.

4 优化设计

由悬架模型的运动学分析可知:该前悬架车轮外倾角符合设计要求，无需进行优化;而前束角在仿真过程中变化范围较大，应对其进行优化以改善行驶过程中车轮的磨损和行驶阻力.

ADAMS/Insight 可用来进行单目标或多目标优化的工具，其本质是在多个设计参数的不同组合中优化设计目标.本研究采用ADAMS/Insight 模块以车轮前束角为优化目标，以摇臂上、下支点2 个坐标点3 个方向共6 个坐标变量为设计参数，以设计目标最小进行优化设计.具体的优化设计步骤如下:

1)确定试验目的.通过调整上、下支点坐标得到合理的车轮前束角变化范围，同时保证其他车轮定位参数在合理变化范围内，分析对前束角影响较大的参数.

2)选择一组需要研究的参数和优化目标.选择上、下支点坐标为参数，仿真过程中车轮前束角绝对值最大值为优化目标，使其变化范围尽可能缩小.

3)确定所选参数的范围，并进行试验.上、下支点位置受悬架其他零件限制，根据具体情况选定其变化范围为± 3 mm.试验策略采用响应曲面法(DOE Response Surface)，选择二次模型来拟合参数和优化目标之间的关系.由于悬架左、右对称，故只选取左边上、下支撑点的3 向坐标(共6 个)作为设计变量，采用全因子法进行优化计算［7］，所需迭代次数为36=729 次.

4)在迭代运算完成后对整个试验过程中设计目标的变化情况进行分析，确定受其影响最大的设计变量.从得出的数据页面可以分析出各个设计变量对优化目标的影响程度(灵敏度).从图6 可以看出，上、下支点的z 方向坐标对前束角影响最大，其次是y 方向，x 方向最小.

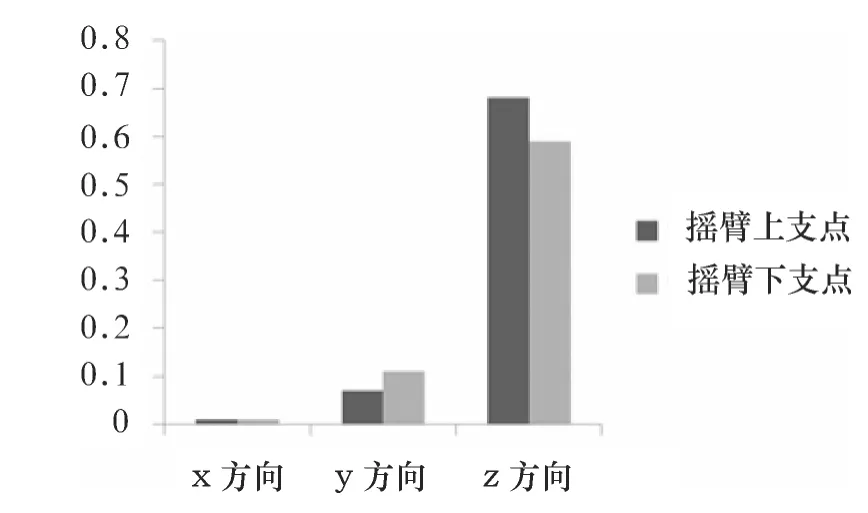
图6 设计变量灵敏度对比

为了达到较好的优化结果以及减少计算量，本研究选取影响程度最大的的设计变量进行优化，同时忽略影响较小的设计变量.对此，在以前束角为优化目标时可选取上、下支点z 方向坐标为设计变量.仿真优化结果如表1 所示.

表1 优化前后z 向坐标

代入优化后的坐标再次对悬架进行仿真分析，图7 所示为优化前、后的前束角变化曲线，实线为优化前，虚线为优化后.可见，经优化后前束角的变化范围为0.12°，大大小于优化前的0.8°，完全达到了优化设计的目标.

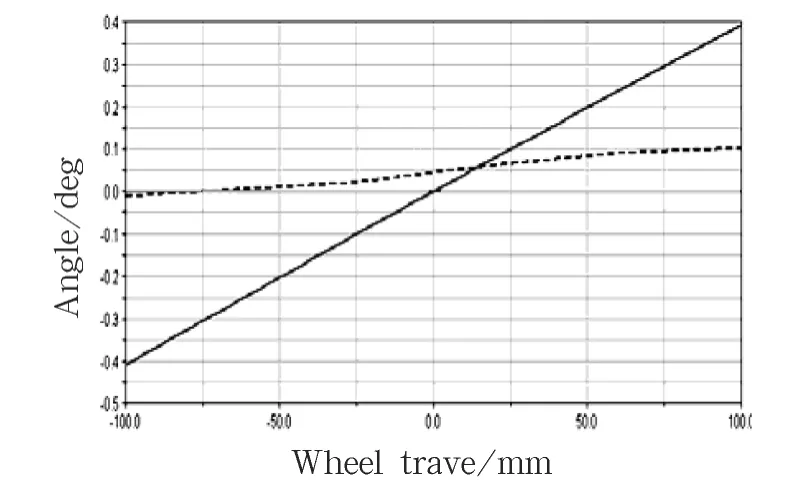
图7 优化前后前束角变化曲线

5 结 论

本研究应用机械系统多体动力学仿真软件，在ADAMS/Car 环境中建立了汽车扭转梁式半独立后悬架刚柔耦合模型，运用ADAMS/Car 实现了扭梁式半独立后悬架的运动学仿真分析，研究了车轮同向跳动激励下主要的车轮定位参数的变化规律.运用ADAMS/Insight 对悬架关键点进行了分析，得出了各主要坐标相对于设计目标前束角变化的灵敏度.在此基础上选取了悬架摇臂上下支点z 方向坐标值为设计变量对其进行优化设计，优化后悬架前束角变化范围大幅缩小.由此可见，利用多体动力学理论进行汽车悬架的参数化建模，并对其运动学性能作出准确分析，利用ADAMS/Insight 优化工具可以快速有效地对设计变量的灵敏度进行分析，有助于选择合适的设计变量进行优化设计，对提高汽车悬架设计的效率及降低成本有极大作用.

［1］Fichera G，Lacagnina M，Petrone F.Modelling of torsion beam rear suspension by using multibody method［J］.Mult Syst Dyn，2004，12(4):303－316.

［2］陈立平，张云清，任卫群.机械系统动力学分析及ADAMS 应用教程［M］.北京:清华大学出版社，2005.

［3］Rao S J，Heydinger G J，Dennis A，et al.Vehicle dynamics modeling and validation for the 2003 ford expedition with ESC using ADAMS view［R］.Warrendale，PA，USA:SAE International，2009.

［4］Zhang L B，Liu H L，Xu Y Z，et al.Study on modeling method of anti-roll bar using one dimensional beam element［R］.Warrendale，PA，USA:SAE International，2009.

［5］谭利也，黄风，徐志刚.麦式后悬架运动学仿真分析及优化［C］//2008 中国汽车工程学会年会.天津，中国:中国汽车工程学会，2008:492－496.

［6］刘进伟，吴志新，徐达.基于ADAMS/Car 的某轿车悬架优化设计［J］.轻型汽车技术，2006，34(8):4－14.

［7］丁亚康，翟润国，井绪文.基于ADAMS/INSIGHT 的汽车悬架定位参数优化设计［J］.汽车技术，2011，42(5):33－36.