基于MATLAB 的图像修复算法的研究与实现
2015-07-31李斌
李斌
(宿州职业技术学院基础教学部安徽·宿州234000)
基于MATLAB 的图像修复算法的研究与实现
李斌
(宿州职业技术学院基础教学部安徽·宿州234000)
随着大数据时代的到来,数据的形态更趋于直观化和系统化,因此图像数据的分析与研究变得更为重要,对大量图像数据的分析与研究要求必须有更加完善和可行的方法,在MATLAB中,可以对大数据中急需处理的破损图像在不同的时间系统里进行更加完善的分析和修复,取得很好的效果。
傅里叶变换图像处理时间系统
1基于MATLAB的连续时间系统的傅立叶分析
对于图像修复过程中的像素及色彩的分析可知,数字图像的缺损往往体现在像素级数变换的不连续和色彩的局部突变,由于以上原因造成对观察者视觉的瞬间冲击,即观察者对图像缺损的瞬间判断。所以,从分析图像的固有的连续特性出发,在连续的时间系统里,可以将数字图像中的相关要素抽象为一个函数f(x),在整个连续系统里利用傅立叶变换进行算法的设计,必会取得一定的破损图像的修复效果。
如下:
设函数f1(t)=e-2|t|,f2(t)=e-0.5|t|,根据MATLAB傅里叶变换可得:函数f1(t)的傅里叶变换:
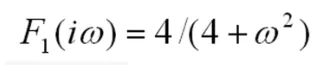
函数的傅里叶变换为:
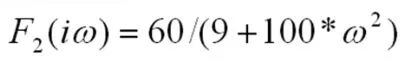
其MATLAB程序如下:
symst
x1=exp(-2*abs(t));
x2=exp(-0.5*abs(t));
F1=fourier(x1);
F2=fourier(x2);
subplot(221);ezplot(x1);
xlabel('t');ylabel('f1(t)');
title('函数f1(t)的图像')
gridon
subplot(222);ezplot(x2);
xlabel('t');ylabel('f2(t)');
title('函数f2(t)的图像')
gridon
subplot(223);ezplot(F1);
xlabel('w');ylabel('F1(iw)');
title('函数F1(iw)的图像')
gridon
subplot(224);ezplot(F2);
xlabel('w');ylabel('F2(iw)');
title('函数F2(iw)的图像')
gridon
可得f1(t),f2(t)f1(iw),f2(iw)的图像如下:
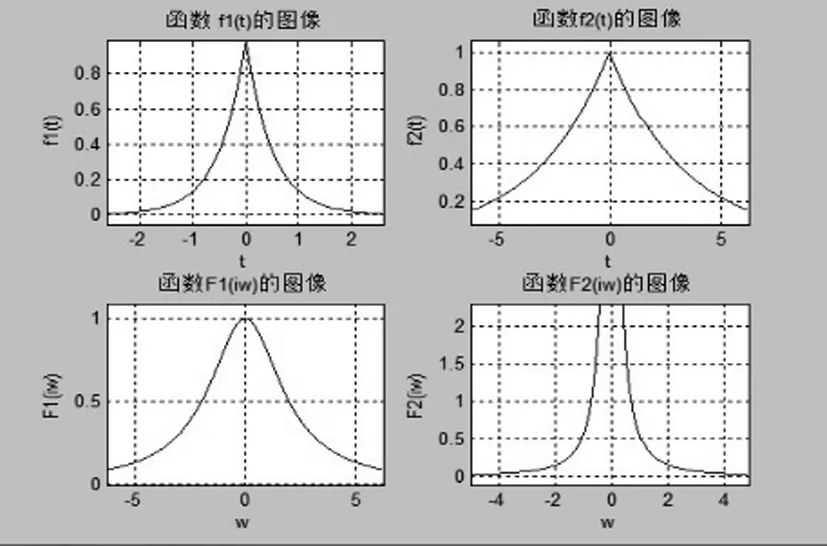
图1连续函数及其频谱图
由图1-1可知,连续时间系统内对函数的自我修复功能有很大的提高,与之对应的数字图像的修复将有较大的提高。
2 基于MATLAB的离散时间系统的傅立叶分析
目前数字图像修复中有很多破损比较严重的图像,这种类型的图像在连续的时间系统里很难较好的修复,因为连续时间系统里要求函数具有很好的连续性,而破算较大的图像往往无法用一个固有的连续函数表示,也就是无法用一个固定的算法一次表现完整,在处理中必需用不同的函数在图像的不同节点处进行模拟,因此对于这一类的图像修复算法的实现必需在一个离散的时间系统里进行分析实现。如下,就是根据抽象出来的节点在MATLAB的离散时间系统里进行的算法设计的程序实现。
已知x(n)=R4(n),X(ejω)=FT[x(n)],绘制相应的幅频和相频曲线,并计算N=8,N=16时的DFT。
程序如下:
N1=8;N2=16;
n=0:N1-1;k1=0:N1-1;k2=0:N2-1;
w=2*pi*(0:2047)/2048;
Xw=(1-exp(-j*4*w))./(1-exp(-j*w));
xn=[(n>=0)&(n<4)];
X1k=fft(xn,N1);
X2k=fft(xn,N2);
subplot(3,2,1);plot(w/pi,abs(Xw));xlabel(‘w/π’)
subplot(3,2,2);plot(w/pi,angle(Xw));axis([0,2,-pi,pi]);line([0,2], [0,0]);
xlabel(‘w/π’)
subplot(3,2,3);stem(k1,abs(X1k),’.’);
xlabel(‘k(w=2πk/N1)’);ylabel(‘|X1(k)|’);holdon
plot(N1/2*w/pi,abs(Xw))
subplot(3,2,4);stem(k1,angle(X1k));
axis([0,N1,-pi,pi]);line([0,N1],[0,0]);
xlabel(‘k(w=2πk/N1)’);ylabel(‘Arg|X1(k)|’);holdon
plot(N1/2*w/pi,angle(Xw))
subplot(3,2,5);stem(k2,abs(X2k));
axis([0,N1,-pi,pi]);line([0,N1],[0,0]);
xlabel(‘k(w=2πk/N2)’);ylabel(‘|X2(k)|’);holdon
plot(N2/2*w/pi,abs(Xw))
subplot(3,2,6);stem(k2,angle(X2k),’.’);
xlabel(‘k(w=2πk/N2)’);ylabel(‘|X2(k)|’);holdon
plot(N2/2*w/pi,angle(Xw))
得到的图像如下:
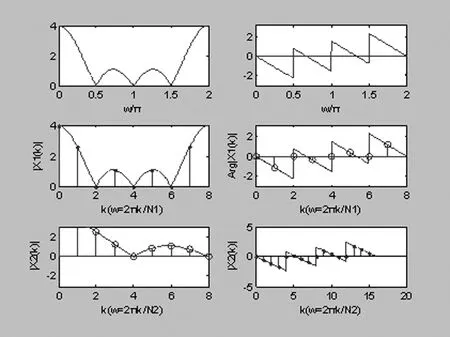
图2离散系统的频率特性曲线
从结果可以看到,所取节点位置、数量不同,得到的图像有很大差异。因此算法设计和程序编写过程中选取适当是节点和注意选取节点的在图像中的分布位置位置以及节点在离散时间系统的里的运算频率对图像修复有着至关重要的影响。
随着云计算、大数据时代的到来,数字图像数据必将成为生产生活中必不可少也是经常处理的数据,因此分析图像数据的不同特点,修复挖掘图像数据的信息,将成为数字分析的主要任务,在MATLAB中对图像修复在不同时间系统的分析与研究对当今的大数据时代有着更加现实的意义。
[1](美)WilliamK.Pratt著·数字图像处理·第三版·北京:机械工业出版社,2005年,120-124.
[2]张勇.数字图像修复关键技术的研究与实现[J].安阳师范学院学报,2014,(02)32-35.
[3]葛仕明.数字图像的修复方法研究[D].博士论文.中国科学技术大学,2008年4月,32-34.
[4]李苏莉.数字图像修复技术的研究与应用[D].硕士论文.西安建筑科技大学,2010年5月,20-23.
TP319.41
A
1009-8534(2015)06-0190-02
2015-09-16
“数字图像修复关键技术的研究与实现”安徽省高校省级自然科学研究项目(KJ2013Z325)。
李斌(1975-),男,安徽濉溪人,硕士,宿州职业技术学院基础教学部副教授;主要从事数学教学和算法理论研究。
