6通道MSVD构造及其在多聚焦图像融合中的应用

刘 斌，刘维杰，魏艳萍

（1.湖北大学计算机与信息工程学院，湖北武汉430062；2.武汉大学计算机学院，湖北武汉430072）

6通道MSVD构造及其在多聚焦图像融合中的应用

刘 斌1，刘维杰2，魏艳萍1

（1.湖北大学计算机与信息工程学院，湖北武汉430062；2.武汉大学计算机学院，湖北武汉430072）

针对经典的奇异值分解（singular value decomposition，SVD）在图像处理中的不足，提出了一种6通道多尺度奇异值分解（multi-scale SVD，MSVD）的构造方法，并将其应用于多聚焦图像融合中。首先，在经典SVD的基础上，利用矩阵分块的方法，给出了一种6通道MSVD的构造方法。其次，对参加融合的多聚焦图像进行6通道MSVD分解，得到高层低频和各层5个方向的高频，对分解的低频子图像采用取平均、高频子图像采用区域能量取大的融合规则进行融合，并进行MSVD逆变换得到融合结果图像。最后，对融合结果图像进行主观分析和客观评价。实验结果表明该方法有好的视觉效果，融合结果图像有较高的清晰度和较丰富的边缘细节信息，且没有方块效应。从客观指标看，该方法有较高的清晰度和空间频率，其清晰度和空间频率比基于离散小波变换、基于提升小波变换、基于曲波变换和基于轮廓波变换的融合方法都高。

图像融合；矩阵奇异值分解；多尺度分析；多聚焦图像

0 引 言

多聚焦图像融合摄取多幅数字图像的较清晰部分，形成一幅各处清晰的新图像，新的图像可以获得场景目标更可靠、全面和更准确的信息，可为计算机进行后续的图像处理提供更清晰的结果图像。近年来，多聚焦图像融合得到了较广泛的发展和应用［1-2］，目前，多聚焦图像融合方法层出不穷，其中，基于多尺度分析的融合方法因其优越的性能而成为多聚焦图像融合方法的主流。自文献［3］提出了图像的金字塔构造方法并应用于图像编码后，各种基于金字塔的图像融合方法被提出，这些金字塔主要有拉普拉斯金字塔［4］、对比度和比率金字塔［56］。张量积小波多尺度分析也是一种金字塔方法，它是具有方向性的金字塔，也被广泛应用于图像融合中［78］。近年来，为了解决张量积小波在图像处理方向上的不足，一些新的基于小波多尺度分析的多聚焦图像融合方法被提出，这些新的小波有多尺度形态学小波［9］，曲波（curvelet）［10-11］，采样和非下采样轮廓波（contourlet）［12-13］，采样和非下采样提升小波（lifting wavelet）等［1416］。基于金字塔的融合方法虽然能实现图像的多尺度融合，但这些方法都不具有方向性，且融合结果图像中会出现人工痕迹和方块效应。基于张量积小波的融合方法虽然具有方向性，但其只注重图像中的水平方向和垂直方向的边缘信息，且由于对滤波后的图像分别进行行、列的下2抽样，使得结果图像中不可避免地会产生方块效应；基于多方向的一类新的小波虽然能提取图像中多个方向的高频信息，但其本质上还是张量积小波，且都依赖于Fourier变换，而且融合时的运算量偏大；基于提升小波的图像融合方法在空间域内进行，不依赖于Fourier变换，速度快，适合于实时图像融合，但目前所使用的提升小波实际上还是张量积小波，它不是二维小波变换的一般形式，因而也只能提取图像中的水平方向和垂直方向的边缘信息，且也不可避免地会产生方块效应。

矩阵或图像的奇异值分解（singular value decomposition，SVD）［17］是一种正交变换，具有高度去相关性，能把信息集中到矩阵的少数行或列上。此方法近年来在图像识别与处理中得到广泛应用。它有如下特点：①能量集中与重新分配。图像的SVD分解是将图像矩阵按特征值的大小对其进行对角化分解，体现了图像能量从大到小的分布特点，主要能量集中于图像的重新处理地后的少数向量上，也就是体现了其主成份分析特性。这种SVD有很好的稳定性，即当图像的灰度值有较小的改变时，图像的奇异值也不会发生较大的变化。SVD既是图像的内蕴特征的表现，也体现了图像能量从大到小的分布规律性，从频率分布的角度看，这种能量从大到小的分布规律也体现了图像频率从低频到高频的分布规律，因而其分解也具有明显的物理意义，也可看成是频率的分解；②具有正交性。能消去像素间的相关性。它使得变换后的图像没有冗余性，因而更适合于图像压缩和融合；③在时域内完成，不需要进行Fourier变换，但也能体现频率特征，有高频和低频；④速度快，能进行实时分解与融合，无需卷积运算，具有线性计算复杂性。

1 SCMSVD构造

1.1 矩阵的SVD

对实数矩阵A∈Rm×n，存在两个正交矩阵U∈Rm×m和V∈Rn×n，使得

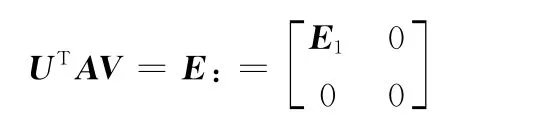
从而矩阵A可分解成3个正交矩阵的乘积，即

式中，E1是大小为m×n的对角阵。若A的秩为r，则E1的对角线上的元素可排列为

显然，A和E1是等价的。因为

即E1的对角线上元素的值是矩阵A的特征值的均方根，这些元素称为A的奇异值。其有较好的稳定性，即当矩阵A的元素的值有较小变化时，其奇异值的改变也不大。奇异值越大，其对应的特征向量拥有的信息量就越多。大的奇异值对应图像的近似部分，即低频部分。而较小的值就对应着图像的细节部分，即图像中的高频部分。因此，如果能将参加融合的图像按照奇异值大小分离出近似信息和细节信息，那么就可以构造出融合图像的多尺度分析［19］。

1.2 SCMSVD构造

为了建立图像的6通道多尺度分析，首先对图像进行分块，对分块后的图像进行分类，形成分类矩阵，计算分类矩阵的奇异值分解，从而构造出一种图像的6通道多尺度分析，具体步骤如下：

步骤1 将图像X∈Rm×n按从上到下、从左到右的方式分成大小为p×q的子块，得到矩阵块序列X（k，l）（1≤k≤m／p，1≤l≤n／q）；

步骤2 将每个子块按先行后列的方式展开为（（p× q）×1）的列向量，再将这些列向量的各元素组合成为一个（p×q）×（mn／（p×q））大小的矩阵T；

步骤3 对T进行SVD分解：T＝USVT，其中U是大小为（p×q）×（p×q）的正交矩阵，V是大小为（mn／（p×q））2的正交矩阵。

步骤4 用得到的UT对T进行线性正交变换（相乘），得大小为（p×q）×（mn／（p×q））的矩阵A，即

步骤5 完成步骤2的逆操作。将A的各个列向量重新排成p×q的子块X，共有mn／（p×q）个子块，将它们重新组合成一个m×n的矩阵X2。

通过上述分解过程后可得到1个低频子图像和（p× q－1）个高频子图像。矩阵A的每一行是正交矩阵U作用于T的结果，U的列向量与奇异值一一对应，U的第一列是最大的奇异值所对应的特征向量。作用后的A的第一行就包含了原图像的主要能量，它是原图像分解出的近似部分，即低频图像。同理，A中其他行包含图像较少的能量，是图像的细节部分，即高频图像。这样便实现了图像的多尺度分解。这样，通过步骤4得到矩阵A后，将A的每一行提取出来按先列后行的顺序重新排列成一个（m／p）×（n／q）的矩阵，分别记为A1，A2…A（p×q），A1就是低频子图像，其他都是高频子图像。

本文中当p×q＝6时就得到6通道的图像分解，由于2×3＝6且3×2＝6，因此，可采用2×3或3×2的方块方式，分解后可得到6幅图像：1个低频子图像和5个高频子图像，分别记作A1，D1，D2，D3，D4，D5。

重构过程是上述分解过程的逆过程。将分解得到的p×q个（m／p）×（n／q）矩阵分别按行、列展开，再组合成（p×q）×（mn／（p×q））的矩阵A*，保留分解时U的值，计算T*＝UA*，然后将T*的列向量还原成p×q的块，再将这些块重新组合，得到一个m×n的重构图像X*。

上述过程只是对图像进行一层SVD分解，对低频子图像A1按上述方式类似地进行多层分解，即得到图像的MSVD构造。

2 图像融合算法

基于6通道MSVD的图像融合流程如图1所示，其主要步骤如下：

步骤1 对参加融合的两幅或多幅多聚焦图像进行位置配准。

步骤2 按第1节的方式分别对参加融合的原图像进行多级6通道MSVD分解，得到最高层一个低频子图像和各层5个高频子图像。

步骤3 对分解后的最高层低频子图像和各层高频子图像按不同融合规则进行融合。

图1 基于SCMSVD的图像融合流程

图像进行MSVD后的低频系数体现的是图像中的近似信息，低频系数越小，表示图像中的低频成分越少，就此而言，低频系数越小越好，然而，低频成份是图像中的主要能量的体现，系数过小，则能量较小，图像的亮度会越低，另外，为了使融合结果图像能尽可能保持参加融合图像的能量的均衡，一般取两幅图像分解后的最高层（空间分辨率最低）的低频系数的平均作为融合结果图像的低频，设A、B分别为参加融合的两幅多聚焦原图像，记A分解后的低频图像为AJ，l，B分解后的低频图像为BJ，l，对所有低频像素点（m，n），则融合图像的低频FJ，l为

为了使融合结果图像充分体现原图像中的清晰部分，选择融合系数时，就要选择能体现原图像进行MSVD分解后能体现原图像清晰部分的系数。图像进行MSVD分解后的高频系数的特性和作用与其他的多尺度分析融合方法的高频系数的方法相同［20］，在对高频图像进行融合时，要尽可能选择绝对值较大的系数作为融合高频子图像的系数。另外，由于图像中的有效目标是以像素块的形式存在的，因此，融合时必须考虑把中心像素和其周围的区域内的像素一起融合，因此，本文对图像MSVD分解的各层高频系数采用基于区域能量取大的融合规则，这样既能很好地考虑图像的清晰度和亮度，又能较好地表现图像中的目标。即图像MSVD分解后的高频系数的融合规则如下：

定义这个窗口的能量为

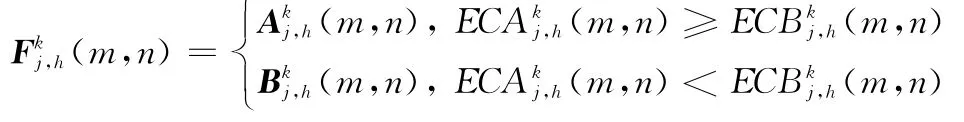
步骤4 对图像分解后的不同层的正交矩阵U进行融合。

U相当于图像分解和重构过程的基，为了使基的作用在参加融合的图像中尽可能平衡，选择参加融合图像分解后的各层的两个U的平均值作为融合结果U的值，具体融合方式如下：

对参加融合的图像A、B，记UA，j为A的第j层分解后的正交矩阵，UB，j为B的第j层分解后的正交矩阵，则第j重构的正交构矩阵为

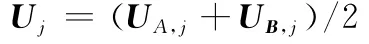
步骤5 按第1节的重构方式对融合后的MSVD塔形结构进行逆变换，得最终融合结果图像。

3 实验结果分析与评价

3.1 实验结果

大量实验结果证实了上述方法是可行而有效的，这里列出实际多聚焦和模拟多聚焦两类图像（每类两组图像）的实验结果，第1类为实际多聚焦图像的融合实验，第2类为模拟多聚焦图像及其融合实验。第1组和第2组为2对实际多聚焦图像的融合实验，其中第1组的源图像如图2（a）、图2（b）所示，是Clock图像，图像大小均为512×512，图2（a）是聚焦左边小钟的图像，图2（b）是聚焦右边大钟的图像；第2组的源图像如图3（a）、图3（b）所示，是Disk图像，图像大小均为480×640，图3（a）是聚焦右边钟的图像，图3（b）是聚焦左边磁盘的图像。第3组和第4组为模拟多聚焦图像融合实验，选定的2幅清晰的标准图像分别如图4（a）和图5（a）所示，图4（a）是大小为512×512的清晰的Lena图像，图5（a）是大小为512×512的清晰的Peppers图像，利用文献［5］的方法分别产生模拟多聚焦图像。图4（b）和图4（c）分别为通过此方法对图4（a）的Lena图像分别进行聚焦于左边和聚焦于右边的图像，图5（b）和图5（c）分别为通过此方法对图5（a）的Peppers图像分别进行聚焦于下面和聚焦于上面的图像。图2（g）、图3（g）、图4（h）和图5（h）分别是利用本文方法对图2（a）和图2（b）、图3（a）和图3（b）、图4（b）和图4（c）、图5（b）和图5（c）进行融合的结果图像。

图2 Clock实际多聚焦图像融合

图3 Disk实际多聚焦图像融合

图4 Lena模拟多聚焦图像融合

为了体现本文方法的融合优势和特点，基于（discrete wavelet transform，DWT）［8］、基于（lifting wavelet transform，LWT）［14］、基于（curvelet transform，CT）［11］以及基于（contourlet transform，CTT）等的融合方法［12］分别与本文方法进行对比研究，这4种方法的融合规则与本文融合规则相同。图2（c）～图2（f）分别是Clock图像分别使用这4种方法得到的融合结果图像，图3（c）～图3（f）分别是Disk图像分别使用这4种方法得到的融合结果图像，图4（d）～图4（g）分别是Lena图像分别使用这4种方法得到的融合结果图像，图5（d）～图5（g）分别是Peppers图像分别使用这4种方法得到的融合结果图像。DWT方法和CTT方法所采用的张量积小波均为Daubechies系列小波中的db2小波。LWT方法使用db2小波的提升小波，基于CTT融合方法所使用的方向滤波器为5－3方向滤波器，所有参与比较的5种方法对源图像的分解层数均为3，使用Matlab7.5编程实现。

图5 Peppers模拟多聚焦图像融合

从融合结果图像可以看出，图2（g）的两个钟都很清晰，图3（g）的Disk和钟都清晰，图4（h）的Lena图像的左右都很清晰，图5（h）的Peppers图像的上下都很清晰。分别比较图2（g）与图2（c）～图2（f）、图3（g）与图3（c）～图3（f）、图4（h）与图4（d）～图4（g）以及图5（h）与图5（d）～图5（g）的融合效果可以看出，本文方法所得结果图像有较好的对比度和清晰度。为了更看清本方法的清晰效果，对融合结果图像使用Canny边缘提取算子分别提取边缘信息，并进行比较。边缘信息越丰富，表明所在融合方法的结果图像越清晰，这里主要列出第一组和第二组实际多聚焦融合中本文方法和基于CTT融合方法的边缘结果图，图2（h）和图2（i）分别是图2（f）和图2（g）的边缘图像，图3（h）和图3（i）分别是图3（f）和图3（g）的边缘图像，比较边缘图像可以明显看出，本文提出的基于MSVD的融合结果图像有较好的边缘信息，文中边缘图像中有明显不同特征的地方都被做上了黄色椭圆标记，可以看出，本文建议方法所提取的边缘更连续、更丰富，从而说明本文方法融合结果更清晰。

3.2 客观性能比较

为了看出各种方法的融合效果，选用图像的清晰度、空间频率指标去衡量各种融合方法的清晰度［21］。

清晰度是利用图像在各点处的图像的水平方向和垂直方向的差分平方和去衡量图像的清晰度的，一幅图像F的清晰度定义为

式中，ΔFx和ΔFy分别表示图像F在x方向和y方向的差分。清晰度的值越大，图像中有较大变化的像素点越多，结果图像越清晰。

图像的行频率定义为

而其列频率定义为

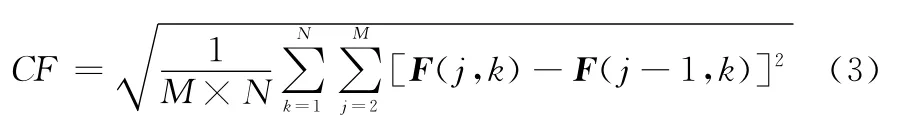
图像的空间总频率是行频率和列频率和合成，即

频率越高，图像的空间分辨力越好，图像越清晰。

表1列出了第1组和第2组实际多聚焦图像的融合性能指标，表2列出了第3组和第4组模拟多聚焦图像的融合的性能指标。比较表1和表2的两列数据可以看出，本文建议的融合方法比采用同样融合规则的基于DWT、基于LWT、基于CT和基于CTT融合方法有较高的清晰度和空间频率。

表1 实际多聚焦图像融合性能评价

表2 模拟多聚焦图像融合性能评价

4 结 论

提出了一种SCMSVD的构造方法，并把它应用于多聚焦图像融合中。这种多尺度构造方法能把图像分解到不同的尺度上，从而对图像的低频和高频可以在不同频率上的轮廓和细节进行融合处理，使融合效果更符合人的视觉特性，同时，图像在不同层分解的5个高频使融合结果图像有更多更好的方向性。另外，这种多尺度分析还保留了SVD的正交性，使得图像分解无冗余；再者，对图像的分解与重构只在空域内完成，不依赖于Fourier变换，从而使图像融合有较快的速度。实验结果表明，该图像融合方法有较好的视觉效果，结果图像有较高的清晰度，边缘细节信息丰富，没有方块效应。从客观性能指标看，该方法有较高的清晰度和空间频率，其清晰度和空间频率比基于DWT、基于LWT、基于CT和基于CTT的融合方法都高。

［1］Bahador K，Alaa K，Fakhreddine O K，et al.Multisensor data fusion：a review of the state-of-the-art［J］.Information Fusion，2013，14（1）：28-44.

［2］Goshtasby A A，Nikolov S.Image fusion：advances in the state of the art［J］.Information Fusion，2007，8（2）：114-118.

［3］Burt P T，Adeson E H.The laplacian pyramid as a compact image code［J］.IEEE Trans.on Communications，1983，31（4）：532 -540.

［4］Yun S H，Kim J H，Kim S K.Image enhancement using a fusion framework of histogram equalization and laplacian pyramid［J］.IEEE Trans.on Consumer Electronics，2010，56（4）：2763-2771.

［5］Liu G X，Yang W H.A Multiscale contrast-pyramid-based image fusion scheme and its performance evaluation［J］.Acta Optica Sinica，2001，21（11）：1336-1342.（刘贵喜，杨万海.基于多尺度对比度塔的图像融合方法及性能评价［J］.光学学报，2001，21（11）：1336-1342.）

［6］Toet A.Multiscale contrast enhancement with application to image fusion［J］.Optical Engineering，1992，31（5）：1026-1031.

［7］Li H，Manjunath B S，Mitra S K.Multi-sensor image fusion using the wavelet transform［J］.CVGIP：Graphical Models and Image Processing，1995，57（3）：235-245.

［8］Pajares G，Cruz G J.A wavelet-based image fusion tutorial［J］.Pattern Recognition，2004，37（9）：1855-1872.

［9］Jiang Y，Wang M H.Image fusion with morphological component analysis［J］.Information Fusion，2014，18（7）：107-118.

［10］Li S T，Yang B，Hu J W.Performance comparison of different multi-resolution transforms for image fusion［J］.Information Fusion，2011，12（2）：74-84.

［11］Wang G，Ma M Z，Zhao Y L，et al.Algorithm for image fusion in the Curvelet transform domain［J］.Chinese Journal of Scientific Instrument，2008，29（9）：1841-1845.（王刚，马美仲，赵英路，等.Curvelet变换域的图像融合算法［J］.仪器仪表学报，2008，29（9）：1841-1845.）

［12］Liu K，Guo L，Chang W W.Regional feature self-adaptive image fusion algorithm based on contourlet transform［J］.Acta Optica Sinica，2008，28（4）：681-686.（刘坤，郭雷，常威威.基于Contourlet变换的区域特征自适应图像融合算法［J］.光学学报，2008，28（4）：681-686.）

［13］Zhang Q，Guo B L.Multifocus image fusion using the nonsubsampled contourlet transform［J］.Signal Processing，2009，89（7）：1334-1346.

［14］Xiao X H，Wu Z H.Image fusion based on lifting wavelet transform［C］∥Proc.of the International Symposium on Intelligence Information Processing and Trusted Computing，2010：659-662.

［15］Geng G Z，Chen H，Liu Y Y，et al.Image fusion method of 9／7 wavelet transform based on lifting scheme［C］∥Proc.of the IEEE International Symposium on Knowledge Acquisition and Modeling Workshop，2008：522-524

［16］Chai Y，Li H F，Guo M Y.Multifocus image fusion scheme based on features of multiscale products and PCNN in lifting stationary wavelet domain［J］.Optics and Communications，2011，284（5）：1146-1158.

［17］Liu R Z，Tan T N.SVD based digital watermarking method［J］.Acta Electronica Sinica，2001，29（2）：168-171.（刘瑞祯，谭铁牛.基于奇异值分解的数字图像水印方法［J］.电子学报，2001，29（2）：168-171.）

［18］Wang X B，Liu B.Multi-focus image fusion based on multi-resolution singular value decomposition［J］.Chinese Journal of Quantum Electronics，2014，31（3）：257-263.（汪晓波，刘斌.基于多分辨奇异值分解的多聚焦图像融合［J］.量子电子学报，2014，31（3）：257-263.）

［19］Kakarala R，Ogunbona P O.Signal analysis using a multiresolution form of the singular value decomposition［J］.IEEE Trans.on Image Processing，2001，10（5）：724-735.

［20］Liu B，Liu W J，Ma J L.Multi-focus image fusion based on three channel nonseparable symmetrical wavelets［J］.Chinese Journal of Scientific Instrument，2012，33（5）：1110-1116.（刘斌，刘维杰，马嘉利.基于三通道不可分对称小波的多聚焦图像融合［J］.仪器仪表学报，2012，33（5）：1110-1116.）

［21］Eskicioglu A M，Fisher P S.Image quality measure and their performance［J］.IEEE Trans.on Communication，1995，43（12）：2959-2965.

Construction of the six channel multi-scale singular value decomposition and its application in multi-focus image fusion

LIU Bin1，LIU Wei-jie2，WEI YAN-ping1
（1.School of Computer and Information Engineering，Hubei University，Hubei Wuhan 430062，China；2.Computer School，Wuhan University，Wuhan 430072，China）

In order to solve the deficiencies of classical singular value decomposition（SVD）in image processing，a construction method of the six channel multi-scale singular value decomposition is presented.An image fusion method based on the multi-scale SVD（MSVD）is proposed.Firstly，based on the principle of classical SVD and blocking algorithm，the six-channel MSVD is performed.Secondly，the images involved in the fusion are decomposed into one approximation and five detail images with different resolution by the MSVD.The fusion rule is that the average value is selected for low-frequency sub-image；while for the high-frequency subimages，the coefficients with larger area energy value are employed.The fused image is obtained by using reconstruction method of the MSVD.Finally，the fusion performance of the result image is evaluated using subjective analysis and objective indices.The experimental results show that the proposed fusion method has good visual effect and has no blocking-artifact in the fused images.When compared with the fusion method based on discrete wavelet transform，lifting wavelet transform，curvelet transform and contourlet transform，the proposed method has been observed to have higher definition and spatial frequency.

image fusion；matrix singular value decomposition（SVD）；multi-scale analysis；multifocus image

N 911.73 文献标志码：A DOI：10.3969／j.issn.1001-506X.2015.09.35

刘 斌（1963 ），男，教授，博士，博士研究生导师，主要研究方向为图像融合、模式识别。

E-mail：liub＠hubu.edu.cn

刘维杰（1991-），男，博士研究生，主要研究方向为信息安全、图像处理。E-mail：lwj20090716＠163.com

魏艳萍（1993-），女，本科，主要研究方向为图像处理。

E-mail：wyp20140616＠163.com

1001-506X（2015）09-2191-07

2014-09-16；

2015-01-16；网络优先出版日期：2015-05-04。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150504.0941.004.html

国家自然科学基金（61471160）；湖北省自然基金重点项目（2012FFA053）资助课题