基于Shearlet域系数处理的SAR图像降噪

2015-07-26刘书君吴国庆张新征徐礼培

系统工程与电子技术 2015年9期

关键词：投影均值边缘

刘书君，吴国庆，张新征，徐礼培

（重庆大学通信工程学院，重庆400044）

基于Shearlet域系数处理的SAR图像降噪

刘书君，吴国庆，张新征，徐礼培

（重庆大学通信工程学院，重庆400044）

结合图像在Shearlet域中系数的特点，提出了一种基于Shearlet系数稀疏表示与投影总变分（total variation，TV）相结合的合成孔径雷达（synthetic aperture radar，SAR）图像去噪算法。有效解决了稀疏表示在图像去噪时存在的边缘细节损失与TV去噪时存在的光滑区域阶梯效应。首先，利用SAR图像Shearlet系数的稀疏性，结合系数稀疏表示模型，采用分段正交匹配追踪方法求解优化解，从统计意义上实现稀疏表示后的系数均值为真实图像系数均值的无偏估计；其次，为弥补稀疏表示中丢失部分系数在图像细节上的损失，同时结合这部分系数对应的Shearlet函数有利于表征图像边缘细节的特性，针对图像在丢失系数对应的Shearlet函数空间中投影重构的结果，结合TV方法迭代去噪。实验结果表明，该方法充分利用Shearlet域系数的特性，采用稀疏去噪与投影TV相结合的方法以弥补各自缺陷，在去噪的同时能有效保持图像纹理细节，并具有更优的图像视觉效果。

合成孔径雷达；图像去噪；稀疏表示；总变分

0 引言

合成孔径雷达（synthetic aperture radar，SAR）的相干成像机理使其获得的图像中含有大量的斑点噪声，这些噪声给目标识别及图像压缩等后期处理带来不利影响［1］。由于SAR图像拥有丰富的纹理和边缘，因此在有效滤除斑点噪声的同时充分保留图像的纹理和边缘，是SAR图像降噪处理的重点。成像后的SAR图像降噪处理可分为以下几类：基于估计理论的方法，如Lee滤波［2-3］、Frost滤波、Map滤波等，其降噪效果的好坏主要取决于噪声分布模型的建立；基于变换域收缩的方法，如小波域滤波［4］、多尺度几何分析滤波等，该类方法根据真实信号在变换域中稀疏的基本原理，运用收缩处理去除噪声对应的系数；基于偏微分方程的滤波方法，如扩散滤波［5-6］等，其优势在于抑制相干斑的同时，可较好地保持图像细节。

近年来，由于稀疏表示在降噪中具有的良好性能，正逐渐成为图像降噪的有效方法之一［78］。由于噪声使图像在变换域中系数的稀疏度大幅降低，如何建立稀疏模型并获得最优解以提高系数的稀疏度便成为降噪的关键。文献［9］提出了基于小波系数稀疏表示的去噪方法，该模型下对应的最优解即为去噪后图像的小波系数，并且均值为干净图像小波系数均值的无偏估计。但该方法在优化问题的求解中对测量矩阵有一定限制，文献［10］以共轭梯度与硬阈值收缩相结合的方法代替文献［9］中的最速下降法，以提高收敛速度并减少对测量矩阵的限制，但阈值的选择是难点，阈值太小会降低系数的稀疏度，影响去噪效果，太大又会影响算法的收敛性。为更好地解决稀疏模型中的优化问题，本文利用分段正交匹配追踪（stagewise orthogonal matching pursuit，St OMP）算法，在满足一定精度的情况下进一步提高算法的收敛速度。

虽然稀疏表示可实现一定程度上的降噪，但丢失系数造成了细节的损失。为解决这一问题，文献［11］提出了基于K-奇异值分解（K-singular value decomposition，KSVD）与投影总变分（total variation，TV）结合的降噪方法，在KSVD降噪的基础上利用TV对降噪后图像的细节进行修复。但由于文献［11］直接对KSVD降噪后的图像进行TV，无法恢复之前丢失的图像信息，其次在扩散项中没有使用各向异性扩散函数，对图像细节的修复能力有限。本文提出的基于Shearlet变换域的系数稀疏表示与投影TV相结合的方法，既利用了稀疏表示对干净图像Shearle系数无偏估计的优势，又充分利用Shearlet系数特性，基于稀疏表示中丢失系数对应的Shearlet函数空间对图像边缘细节的提取能力，针对图像在该空间的投影结果采用TV处理。由于稀疏表示与TV相互结合，不仅可利用基于投影的TV处理恢复稀疏表示中丢失系数对应的细节，同时利用稀疏表示的去噪能力也可以降低TV处理在平滑区域存在的阶梯效应，使细节区域与平滑区域的降噪性能都得以提高。

1 Shearlet变换及系数特性

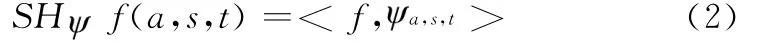
对尺度矩阵和剪切矩阵进行离散处理，即a＝2j（j∈ Z），s＝l（l∈Z），可得离散Shearlet为

式中，j为尺度参数；l为剪切参数；k为平移参数。A和B均为2×2可逆矩阵，｜det B｜＝1。如果此系统满足紧框架，则该系统中的元素称为合成小波。

Shearlet系数不仅具有稀疏性，根据文献［12］的证明，当t处于边缘Γ上，且s与Γ上t处对应法向量方向一致时，a趋于0，Shearlet系数衰减速率最慢。因此当a趋于0时，可利用并根据不同尺度间的衰减速度区分图像中的噪声峰值与边缘。本文正是基于Shearlet的性质，不仅利用Shearlet系数的稀疏特性进行去噪，同时利用Shearlet对图像边缘信息的捕获能力，结合投影TV实现对图像的去噪处理。

2 Shearlet域稀疏表示

由于SAR图像为乘性噪声，为便于稀疏表示，首先采用式（4）的处理将乘性噪声转化为加性噪声。

式中，F为被噪声污染的图像强度；R代表相干斑噪声；X代表地物真实的后向散射强度，且R和X为相互独立的随机过程。若R服从均值为1，方差为1／L的gamma分布，则噪声N＝（R－1）X为0均值的加性噪声。

由于对大部分干净图像的Shearlet系数比小波系数具有更稀疏的表示，因此可基于图像Shearlet系数的稀疏表示实现对图像的降噪。首先建立如式（5）的稀疏表示模型［9］。

假设ˆw表示含噪图像在某一尺度和方向上Shearlet系数，大小为N×N，ΦM×N为满足一致不确定原理的随机矩阵，其中M＜N，‖‖0表示0范数，正则化参数γ在保真项和正则项之间进行平衡，以实现系数的稀疏表示。首先用测量矩阵Φ对系数w进行变换，即y＝Φw。进一步假设y在字典Φ下的稀疏逼近表示为z，为求解式（5），令

可见，当式（6）取最小值时对应最优解z即为原系数w的稀疏表示ˆw。由文献［9］证明可知，当所加噪声为零均值，测量矩阵满足弱限制条件时，无论含噪图像系数w的稀疏度大于、等于或小于干净图像系数的稀疏度，稀疏表示ˆw的均值均为干净图像Shearlet系数均值的无偏估计。

由于图像在不同尺度下剪切波变换系数的数据量较大，为提高算法收敛速度，本文采用StOMP方法求解式（5）。与OMP不同之处在于其每次迭代时按照一定标准选择出一个或者多于一个的原子，从而提高追踪速度［13］。St OMP算法初始时稀疏逼近值z0＝0，残差R0y＝y，所选原子下标索引集I0为空。当迭代次数m＝1时，首先求R0y与Φ各原子的内积，即R0y在各原子上的投影，然后引入硬阈值t1并通过式（7）选择与R0y最匹配的几个原子。

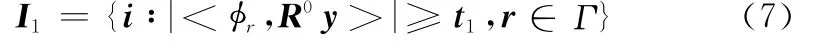
正交化所选原子，重新将R0y投影到正交化的原子上，得到第一次稀疏逼近后的残差R1y，判断索引集中原子下标个数是否小于设置的稀疏度L，若小于则继续迭代。当循环结束，由式（8）得最优解zm。

最优解zm即为原系数w的稀疏表示ˆw，再将稀疏Shearlet系数ˆw重构回图像域，即可得去噪后的图像us。图1（a）为干净的自然图像Lena，图1（b）为含有乘性噪声的图像，图1（c）为Shearlet稀疏表示降噪后的图像us。由于稀疏表示中丢弃了部分系数，降噪后的图像相比于原图像存在细节上的模糊。将丢失部分系数重构出的图像ud如图2（a）所示，与干净图像在相同系数对应Shearlet函数空间投影的结果u′d（见图2（b））进行对比，可知图像ud中包含有大量噪声和纹理细节。为达到去噪同时保持细节纹理的目的，以下采用Shearlet域投影TV的方法进行进一步的处理。

图1 Lena对比图

图2 残差图像

3 基于Shearlet域投影的TV去噪

由稀疏表示的原理可知，丢失部分的Shearlet系数均为趋于零的系数。结合前文对Shearlet系数的特性分析，当a趋于零时，SHf（a，s，t）的衰减速度可用于区分图像中的边缘与噪声。可见，这些丢失的系数不仅包含有稀疏表示中损失的图像信息，而且可用于提取图像边缘细节，根据这一特性结合基于能量泛函的TV模型，给出如式（9）的TV去噪模型。

式中，u0为处理前的含噪图像；‖‖为标准欧式范数；φ∈C2（R）为正则化函数［14］；λ为正则参数［15］。式（9）右端第一项为正则项，保证解u具有一定的正则性及特定区域中的非连续性；第二项为保真项，以保留原图像特性。其中Ps（u）如式（10）所示。

式中，M为j，k，l所属集合，该集合由前文稀疏表示中丢失系数对应的Shearlet函数确定；Ps（u）表示图像u在选定部分Shearlet函数空间上投影重构的结果。当∂u／∂t＝0时，式（9）的能量泛函取极小值，此时u即为TV处理后的去噪图像。由式（9）可得∂u／∂t如式（11）所示。

式中，第一项为扩散项，令ρ（x）＝φ′（x）／x［16］（其中x＝‖ΔPs（u）‖），

在含噪的非边缘区域中x值较小，对应ρ（x）较大，扩散程度强，在边缘区域x较大，对应扩散程度减弱。可见，ρ（x）可对扩散过程中的平滑度进行控制。为求解式（11）给出离散形式

式中，Δt为离散时间步长；k＝0，1，…，L－1；η（u）＝Δ（（φ′（‖Δu‖）Δu）。在首次迭代时，结合前文稀疏表示后获得的去噪图像us及丢失部分系数重构出的图像ud，将us+Δt·η［ud］的结果作为初始化5×5，并令λ＝0，代入式（12）经过σ2次处理，得到首次迭代后修复的图像。在第β＝5次迭代中得到的修复图像Δt＝0.1作为第i+1次迭代中的初始值，即＝，并令λ＝0.2，由式（12）经过L次处理得到第i+1次迭代后的修复图像，直到与的平均绝对偏差（mean absolute deviation，MAD）小于某一门限ε时结束迭代，获得最终的修复图像。

综上所述，基于Shearlet系数处理的SAR图像降斑算法如下：

步骤1 通过式（4）将乘性噪声模型转化为加性噪声模型；

步骤2 对含噪图像u0进行Shearlet变换，得到不同尺度下Shearlet系数w；

步骤3 利用StOMP算法求解式（6）给出的稀疏表示模型，得到统计均值上干净图像的Shearlet系数；

步骤4 对系数进行Shearlet反变换得降噪后图像us，并将w中丢掉的小系数重构为残差图像ud，并将该部分系数对应的Shearlet函数集合记为M；

步骤5 将us+Δt·η［ud］作为首次迭代初始值，令λ＝0，由式（12）得到第一次迭代修复后的图像；

步骤6 在第i次迭代中，令＝，结合λ＝0.2，利用式（12）经过L次循环求得第i次迭代后的；

步骤7 重复步骤6，当与的MAD小于设置门限时停止迭代，得到最终降噪图像。

4 实验结果与分析

首先分析图3所示的两张模拟2视数SAR图像Lena和Hill的降噪情况，并采用以下参数进行分析：图像的峰值信噪比（peak signal to noise ration，PSNR），其值越大就表示在数值上降噪后的图像越接近于干净图像；降噪后图像与干净图像间的平均绝对误差（mean absolute-deviation error，MAE）［11］，其值越小整体降噪能力越强；两幅图像间的相似度（structural similarity，SSIM）［18］，其值越接近于1表明降噪后图像与原始干净图像在结构和亮度上越接近。

图3 视数L＝2时两幅含乘性噪声的图像

去噪后的图像如图4和图5所示。

图4 对Lena图像去噪后的图像

图5 对Hill图像去噪后的图像

由图4和图5可见，本文算法在实现降噪的同时可较好地保持图像边缘与细节信息。为进一步分析算法的性能，表1给出当视数L＝2时，各降噪算法对图3中Lena和 Hill图像处理后的性能参数。由表1可知，本文算法的PSNR明显高于其他算法，不仅具有较强的降噪能力，同时在图像结构亮度保持方面也有一定优势。

表1 对含乘性噪声图像各种降噪算法的性能参数

为进一步体现本文方法处理真实SAR图像的性能，以图6（a）和图6（b）为真实的SAR图像，大小均为512×512，X波段的强度图像。Real-SAR1分辨率为3 m×3 m，来自MSTAR数据。Real-SAR2分辨率为1 m×1 m，来自Radarsat-2数据。图7和图8分别给出对Real-SAR1和Real-SAR2图像经不同算法降噪处理后的结果。

由图7和图8可见，Lee滤波处理后仍然含有少量噪声，同时在边缘保持方面相对较差；KSVD具有良好的稀疏表示能力，图7（b）中的噪声已基本去除，但图像的细节也有所损失；图7（c）采用KSVD＿TV仅针对KSVD降噪后的图像进行TV修复，并不能找回降噪中损失的边缘细节，所以修复效果并不明显；由Shearlet.TV与本文算法处理结果对比可见，本文所提算法对平滑区斑点噪声抑制能力更强，降噪后图像边缘细节信息得到了更好的保持，抑斑后的图像较为清晰。图8是针对Real-SAR2图像的处理结果，各算法的性能表现与处理Real-SAR1图像相似，在图像质量和视觉效果方面均得到了较好的改善。

图6 真实SAR图像

为比较各种方法对细节区域与平滑区域的降噪处理能力，在图6（b）中选择了一块包含细节与平滑的区域进行分析，如图9所示。在图6（b）所示的Real-SAR2图像中选择了两块白色矩形同质区域。采用均值μ、方差σ2、等效视数（equivalent numbers of looks，ENL）作为降噪性能评价指标。理想降噪方法降噪后图像的均值应与降噪前保持一致；降噪后图像同质区方差越小表示相干斑抑制能力越强；ENL是衡量一幅SAR图像斑点噪声相对强度的一种指标，ENL越大，表明图像上斑点越弱，可解译性越好。表2给出了对同质区1、2进行降噪处理的性能参数实验结果。

图7 对Real-SAR1图像去噪后的图像

图8 对Real-SAR2图像去噪后的图像

图9 对细节图像的各算法处理结果

表2 对同质区1、2不同去噪算法的性能参数

由图9可见，本文方法在细节处理能力上强于KSVD及KSVD＿TV，由于采用和Shearlet.TV方法类似的投影TV提取细节，因此图9（f）与图9（e）的细节保持能力相当。对比图9（f）和图9（e）中平滑区域可见，由于本文方法结合稀疏表示对Shearlet系数进行去噪处理，可避免TV处理中在平滑区域的阶梯效应，因此本文方法对平滑区的降噪性能优于Shearlet.TV的降噪能力。

从表2的均值可见，本文算法降噪后图像均值最接近真实图像的均值，在降噪的同时可较好保持雷达辐射特性。由方差可见，本文算法大大降低了同质区方差，从ENL值来看，本文算法的性能优于其他算法，更有利于图像的解译。

5 结束语

本文在Shearlet域中结合稀疏表示与TV实现SAR图像降噪，充分利用了图像Shearlet系数的稀疏性与提取图像边缘的能力。首先通过稀疏表示后保留系数为干净图像系数无偏估计的优势进行降噪，并采用StOMP算法求解稀疏模型的优化解，在保证精度的情况下提高运算效率。由于稀疏表示中存在丢失系数带来图像细节损失的问题，本文进一步结合丢失部分Shearlet系数对图像噪声和边缘细节的区分能力，针对图像在丢失系数对应Shearlet空间中投影重构的结果，采用基于能量泛函的TV处理，在降噪的基础上实现对损失信息的修复。实验结果表明本文方法不仅具有很好的降噪效果，还能有效地保持图像纹理细节。然而本文算法并没有考虑图像内在的结构性，如果利用先验信息结合聚类分块的方法应该会取得更好效果。

［1］Argenti F，Alparone L.Speckle removal from SAR image in the undecimated wavelet domain［J］.IEEE Trans.on Geoscience and Remote Sensing，2002，40（11）：2363-2374.

［2］Liu L，Chen Y Q.Modifed InSAR phase Lee filter［J］.Science Technology and Engineering，2013，13（19）：5668-5672.（刘璐，陈永强.改进的InSAR相位Lee滤波器［J］.科学技术与工程，2013，13（19）：5668-5672.）

［3］Lee J.Refined filtering of image noise using local statistics［J］.Computer Graphics and Image Processing，1981，15（4）：380-389.

［4］Gleich D，Datcu M.Wavelet-based despeckling of SAR images using Gauss-Markov random fields［J］.IEEE Trans.on Geoscience and Remote Sensing，2007，45（12）：4127-4143.

［5］Gramfort A，Poupon C，Descoteaux M.Denoising and fast diffusion imaging with physically constrained sparse dictionary learning［J］.Medical Image Analysis，2014，18（1）：36-49.

［6］Che J，Guan Q，Wang X Y.Image denoising based on adaptive fractional partial differential equations［C］∥Proc.of the 6th International Congress on Image and Signal Processing（CISP），2013：288-292.

［7］Lu X Q，Yuan Y，Yan P K.Sparse coding for image denoising using spike and slab prior［J］.Neurocomputing，2013，106（4）：12-20.

［8］He Y M，Gan T，Chen W F.Two level image denoising based on sparse representation［J］.Electronics&Information Technology，2012，34（9）：2268-2272.（何艳敏，甘涛，陈武凡.基于稀疏表示的两级图像去噪［J］.电子与信息学报，2012，34（9）：2268-2272.）

［9］Zhao R Z，Liu X Y，Li C C，et al.Wavelet denoising via sparse representation［J］.Science in China Series F，2009，52（8）：1371-1377.

［10］Liu S Q，Hu S H，Yong Y X，et al.Bayesian Shearlet shrinkage for SAR image de-noising via sparse representation［J］.Multidimensional Systems and Signal Processing，2014，25（4）：683-701.

［11］Hao Y，Feng X C，Xu J L.Multiplicative noise removal via sparse and redundant representations over learned dictionaries and total variation［J］.Signal Process，2012，92（6）：1536-1549.

［12］Guo K，Labate D，Lim W.Edge analysis and identification using the continuous shearlet transform［J］.Applied and Computer，2009，27（1）：24-26.

［13］Donoho D L，Tsaig Y，Droril I，et al.Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit［J］.IEEE Trans.on Information Theory，2012，58（2）：1094-1121.

［14］Blanc-Feraud L，Charbonnier P，Aubert G，et al.Nonlinear image processing：modelling and fast algorithm for regularization with edge detection［C］∥Proc.of the IEEE International Conference Image Processing，1995：474-477.

［15］Rudin L，Osher S，Fatemi E.Nonlinear total variation based noise removal algorithm［J］.Physcia D，1992，60（1／4）：259-268.

［16］Perona P，Malik J.Scale-space and edge detection using anisotropic diffusion［J］.IEEE Trans.on Pattern Analysis and Machine Intelligence，1990，12（7）：629-639.

［17］Easley G R，Labate D，Colonna F.Shearlet-based total variation diffusion for denoising［J］.IEEE Trans.on Image Processing，2009，18（2）：260-268.

［18］Liang D，Liang Z，Bao W X，et al.Image denoising algorithm of non local regularization based on sparse representation［J］.Systems Engineering and Electronics，2013，35（5）：1104-1109.（梁栋，梁昭，鲍文霞，等.基于非局部正则化稀疏表示的图像去噪算法［J］.系统工程与电子技术，2013，35（5）：1104-1109.）

SAR image denoising via the process of shearlet coefficients

LIU Shu-jun，WU Guo-qing，ZHANG Xin-zheng，XU Li-pei
（College of Communication Engineering Chongqing University，Chongqing 400044，China）

Combined with the characteristics of the coefficients in the Shearlet domain，an synthetic aperture radar（SAR）image denoising method is presented based on the sparse representation of coefficients and projected total variation（TV）method.The problem that the edge details of the image often lost in the processing of sparse representation and the staircasing effects caused by total variation can be resolved by the proposed method.Firstly，the sparse representation model of the SAR image is constructed and the stagewise orthogonal matching pursuit（St OMP）is used to obtain the optimization solution，which is the unbiased estimation of the real image's coefficients in terms of the statistical mean.Secondly，to make up the loss of the image details result from the coefficients dropped in the sparse representation processing，the projected total variation scheme is given to iterative denoising，that utilizes the property of the dropped coefficients have the ability to characterize edges of Shearlet coefficients and projects the image to the Shearlet functions that corresponding to these dropped coefficients to get the reconstructed image.The experimental results demonstrate that the proposed method combines the sparse denoising and projection TV based on the characteristics of coefficients in Shearlet domain，that corrects their respective defaults not only suppresses the speckle but also achieves better performance in terms of effectively maintaining the image texture details and subjective visual quality.

synthetic aperture radar（SAR）；image denoising；sparse representation；total variation

TN 957.52 文献标志码：A DOI：10.3969／j.issn.1001-506X.2015.09.11

刘书君（1981-），女，讲师，博士，主要研究方向为SAR图像处理、SAR成像与目标检测。

E-mail：liusj＠cqu.edu.cn

吴国庆（1990-），男，硕士研究生，主要研究方向为图像处理、稀疏信号处理。

E-mail：gqwu0818＠126.com

张新征（1978-），男，副教授，博士，主要研究方向为SAR目标识别、图像处理、信号处理。

E-mail：zhangxinzheng＠cqu.edu.cn

徐礼培（1992-），女，硕士研究生，主要研究方向为SAR图像处理、统计信号分析。

E-mail：lipeixu03＠126.com

1001-506X（2015）09-2023-06

2014-12-01；