高频地波雷达飞行目标高度属性判别

2015-07-26赵孔瑞于长军刘爱军菅维乐权太范

系统工程与电子技术 2015年9期

关键词：飞行高度电波低空

赵孔瑞，于长军，刘爱军，菅维乐，权太范

（1.哈尔滨工业大学电子与信息工程学院，黑龙江哈尔滨150001；2.哈尔滨工业大学（威海）信息与电气工程学院，山东威海264200）

高频地波雷达飞行目标高度属性判别

赵孔瑞1，于长军2，刘爱军2，菅维乐2，权太范2

（1.哈尔滨工业大学电子与信息工程学院，黑龙江哈尔滨150001；2.哈尔滨工业大学（威海）信息与电气工程学院，山东威海264200）

高频地波雷达飞行目标高度估计一直是工程上尚未解决的热点问题。然而在实际工程应用中，更加关心的是被探测到的飞行目标是高空还是低空的高度属性问题，而且飞行目标高度属性判别研究比精确估计目标的具体飞行高度更有实际应用意义，且更容易在实际系统中实现。基于上述工程设计思想，提出高频地波雷达飞行目标高／低属性判别工程化方法，首次解决了高频地波雷达飞行目标高度属性判别问题。所提方法利用垂直极化电波在高空和低空高度区域的不同电波传播衰减特性构建高度属性判别算法，不仅判别目标高度属性，而且给出高度属性判别可信度。实测数据处理表明，所提方法能够利用少量观测数据快速判别飞行目标高度属性，可信度达到90%以上。

高频地波雷达；高度属性；电波传播衰减

0 引言

高频地波雷达（high frequency surface wave radar，HFSWR）发射垂直极化电磁波沿海面传播衰减较小的特点，能够探测数百公里外的海上飞行目标［14］，为海监部门打击海上走私、海上交通管制、专属经济区保护提供了新途径和手段［5-7］。HFSWR利用电波传播绕射机理可以探测到超视距飞行目标，同时由于HFSWR垂直波束较宽，还可以探测到高空视距目标。但是，目前HFSWR只能获取目标的距离和方位信息，不能直接获取飞行目标的高度信息，因而无法判别目标高度属性，即无法判别是高空目标还是低空目标。正如文献［8］所指出的那样“这种雷达不能立即区别在视线范围内位于同一超过地平线距离上而有不同高度的目标”。

为判别飞行目标的高／低空属性，可以利用传统方法先精确估计目标飞行高度再判别目标飞行高度属性。但是目前HFSWR都是利用斜距和方位信息估计高空目标的飞行高度，这些方法不能适用于低空飞行目标高度估计问题。文献［9］利用HFSWR信号回波强度提出了一种目标高度和目标散射截面积（radar cross section，RCS）的实时估计方法。但是这种方法在高度估计时是一个多解问题，高度估计误差较大，高度估计结果可信度低。虽然基于上述方法提出了许多改进算法，但仍然没有从根本上解决高度估计的多解问题［10-12］，至今无法应用于HFSWR实际系统中。从工程应用角度看，HFSWR飞行目标高度估计仍处于探索阶段。在HFSWR海上飞行目标预警应用中，往往更关心目标是低空飞行状态还是高空飞行状态。能够直接、快速判别飞行目标是高空还是低空属性，即获取飞行目标高度属性比精确估计目标的具体飞行高度更有实际应用意义，而且更容易在实际HFSWR系统上实现，也从而回答文献［8］提出的HFSWR探测飞行目标无高度判别的问题。

基于上述工程设计思想，本文重点解决HFSWR飞行目标低空／高空属性判别问题。利用垂直极化电波在高空和低空高度范围内的不同传播衰减特性提出一种目标高度属性判别算法，而不估计目标具体飞行高度。这种方法不仅判别目标高度属性，而且还给出高度属性判别可信度。最后通过实测数据对本文提出的方法进行验证。

1 HFSWR传播衰减

根据单基地HFSWR方程可以得到接收站信号回波强度为

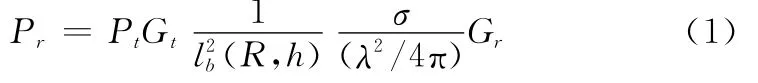
式中，Pr为接收信号回波强度；Pt为发射站信号发射功率；Gt为发射天线增益；Gr为接收天线增益；σ为目标RCS；h为目标高度；R为目标距离雷达观测站的距离；lb（·）表示国际电信联盟采用的地波传播衰减，其是目标飞行高度h和目标距离R的函数；λ表示发射站雷达工作频率。

将雷达方程式（1）取对数，可得分贝形式下的表示形式为

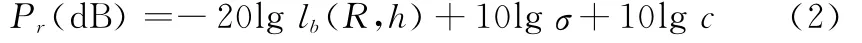
令

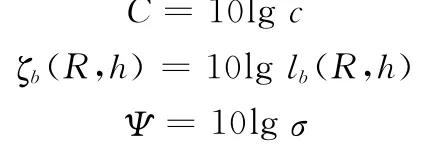
那么，式（2）表示为

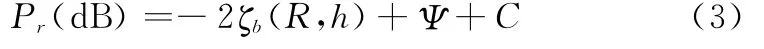
由HFSWR方程式（3）可知，假设雷达系统参数恒定，那么C也是已知的。目标回波强度Pr是传播衰减ζb（R，h）和飞行目标RCSΨ的二元函数。将信号回波强度看作一个已知的常量，目标RCS和电波传播衰减之间具有线性约束关系。此外，电波传播衰减ζb（R，h）是目标距离和飞行高度的函数。因此，要实现目标飞行高度属性判别，需要分析垂直极化电波传播在不同高度上的传播衰减特性。

在高频波段，Rotheram模型考虑了大气的折射指数，并对传播衰减模型进行了详细的理论推导，其传播衰减曲线被国际电信联盟采纳为10 k Hz～30 MHz的地波传播衰减标准［13-14］。因此，基于Rotheram传播衰减模型的独特优势，本研究中采用Rotheram传播衰减模型计算不同高度和距离上的传播衰减曲线。首先，根据Rotheram模型给出一个传播衰减的例子。在雷达工作频率10 MHz，发射站高20 m，雷达站和目标之间距离为40～140 km的范围内，目标飞行高度分别在高空区域和低空区域可以得到传播衰减曲线如图1和图2所示。

图1 低空域地波传播衰减

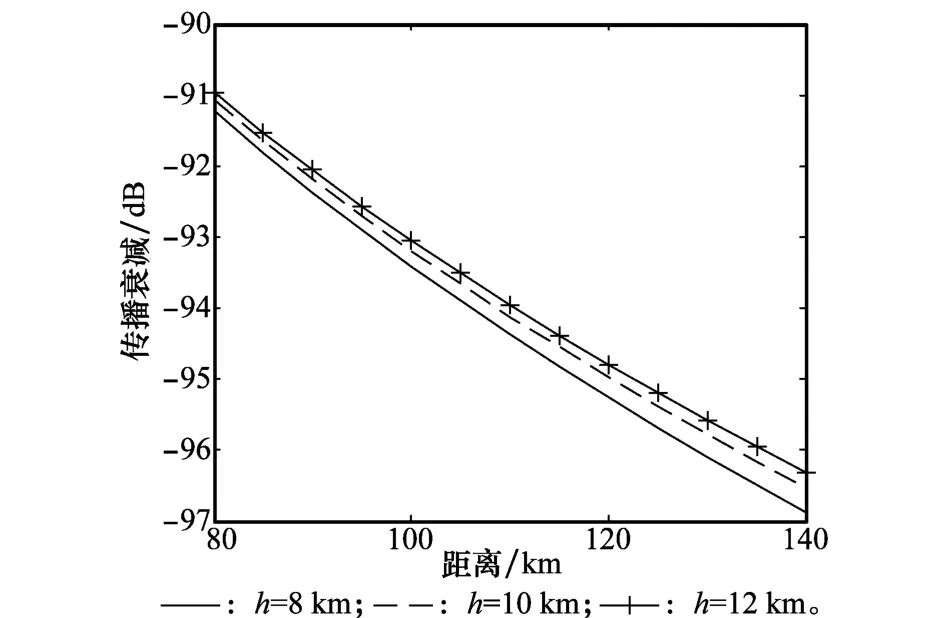
图2 高空域地波传播衰减

由图1和图2可见，地波传播衰减曲线在不同高度上都随着距离的增大而增大；在高度方向上随着高度的增加，衰减逐渐减小。此外，由图1可见，当飞行高度低于2 km时，不同高度上的衰减曲线区分比较明显，高度变化0.5 km时可以引起2 dB的偏差。而在高空空域，由图2可见，随着高度的增大，在不同高度上的传播衰减差别越来越小，即使从8 km增大到12 km，在距离140 km处的传播衰减仅仅减小0.58 dB；当目标距离更近时，传播衰减差别越不明显。例如，目标距离为80 km时，传播衰减之差仅仅为0.26 d B。由此可见，在高空区域传播衰减区别不明显。这是因为随着高度的增加，海面效应对电波传播衰减的影响越来越小，垂直极化电波衰减越来越近似于大气传播衰减。因此，垂直极化电波传播衰减在高空和低空区域的不同传播衰减特性为目标飞行高度属性判别提供了可能。

2 高度属性判别算法

为简化问题分析，假定目标具有两种高度属性：低空属性和高空属性，分别用Dh和Dl表示。同时假设感兴趣的低空范围为0～2 km，高空范围为7～12 km。由垂直极化电波传播衰减特性可知，目标飞行高度较高时，高度信息对信号回波强度的影响很小，可以忽略高度对信号回波强度的影响。因此，用目标高度为10 km处的传播衰减代替高空区域内任意高度上的传播衰减。那么，式（3）可以重新定义为

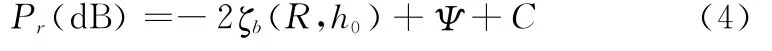
式中，h0＝10 km。

定义目标状态向量为

式中，Ψ为目标相对于观测站的RCS大小；vΨ为目标RCS变化率。假定飞行目标相对观测站的姿态角是慢变化的，那么目标RCS也是慢变化的。则定义目标状态方程为

式中，F∈R2×2为状态转移矩阵；v（k）为零均值、白高斯过程噪声。

由信号回波强度可定义量测值为

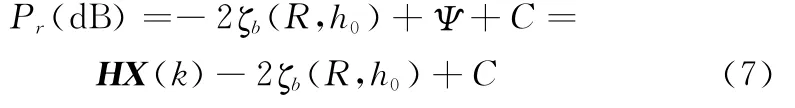
式中，H∈R1×2是量测矩阵；H＝［1 0］。式（6）和式（7）构成了高空飞行状态下的目标高度属性判别模型。

目标在低空飞行状态下，由海面作用引起的地波传播附加衰减影响较大，即使在目标飞行高度上升0.5 km的情况下，传播衰减将减小2 dB以上。因此，假定在2 km以下的区域为低空区域，将高度0～2 km的范围划分为4个高度子空间，高度划分节点分别为h1＝0.5 km，h2＝1 km，h3＝1.5 km。在每个高度节点上分别建立高度属性判别模型。即每个高度子区间的属性判别量测模型为

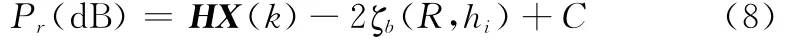
式中，i＝1，2，3。

因此，为实现目标高度属性判别，可以在每个高度属性区间利用式（8）建立相应的判别模型，其中，h0表示高空属性；hi（i＝1，2，3）表示低空属性。然后利用多假设思想，在每个高度区间上分别建立独立的状态估计模型，此处的状态估计模型重点不是估计目标状态信息，而是利用每个模式下的状态估计信息来求解每个高度属性判别的可信度，依据可信度的大小对目标飞行高度属性进行判别，而不必考虑状态估计精度。定义高度属性可信度如下：

（1）高空属性可信度

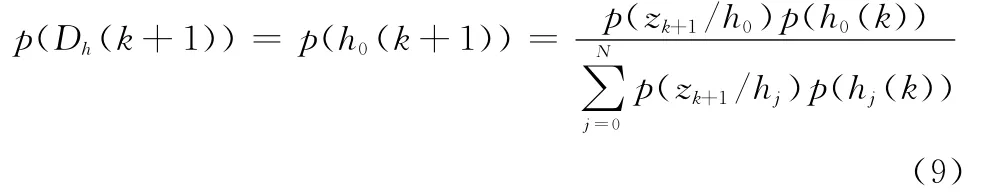
（2）低空属性可信度

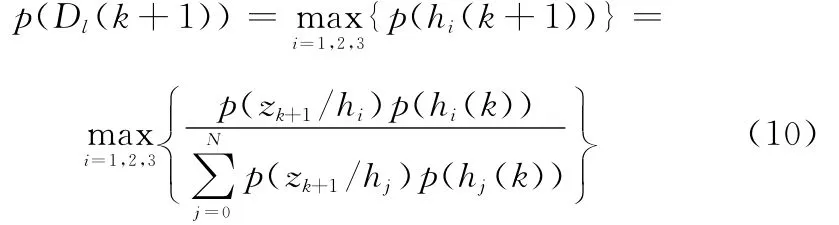
式中，N＝3；p（hi（k））（i＝1，2，3）为第i个高度区间模型的概率大小；p（zk+1／hi）为k+1时刻目标处于hi高度区间时的量测似然函数。假设量测噪声为零均值高斯白噪声，量测似然函数p（zk+1／hi）可以表示为

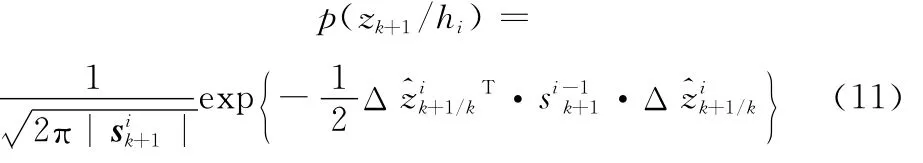
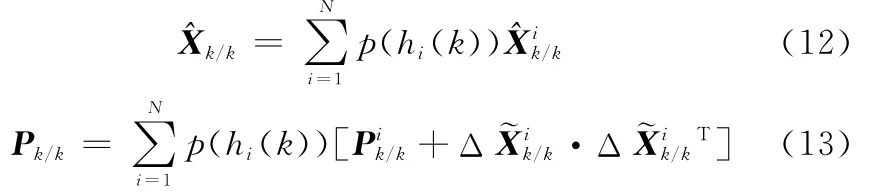
3 实测数据验证

为验证高度属性判别算法的有效性，利用实测数据对其进行验证。雷达工作频率为11.4 MHz，发射功率为1 k W。飞行目标相对于高频地波雷达站的飞行航迹如图3所示，目标飞行高度为200 m，相对于雷达观测站方位角为14°。高度属性判别如图4所示。

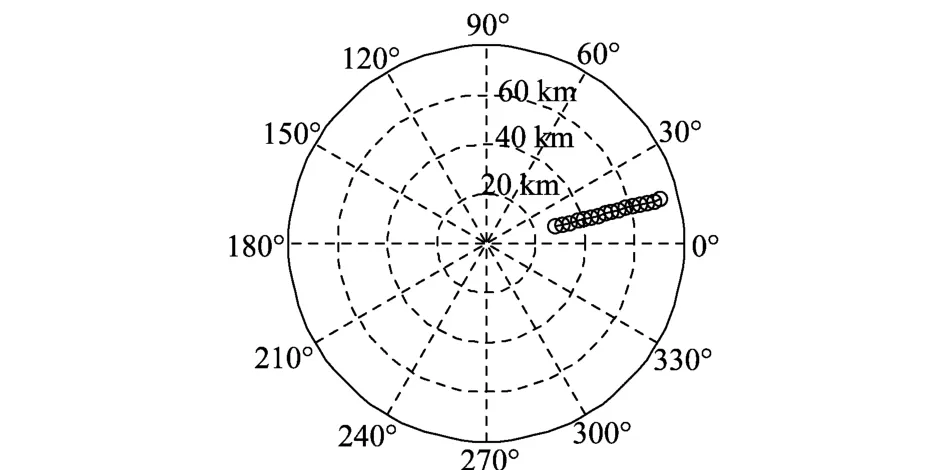
图3 目标相对于观测站航迹

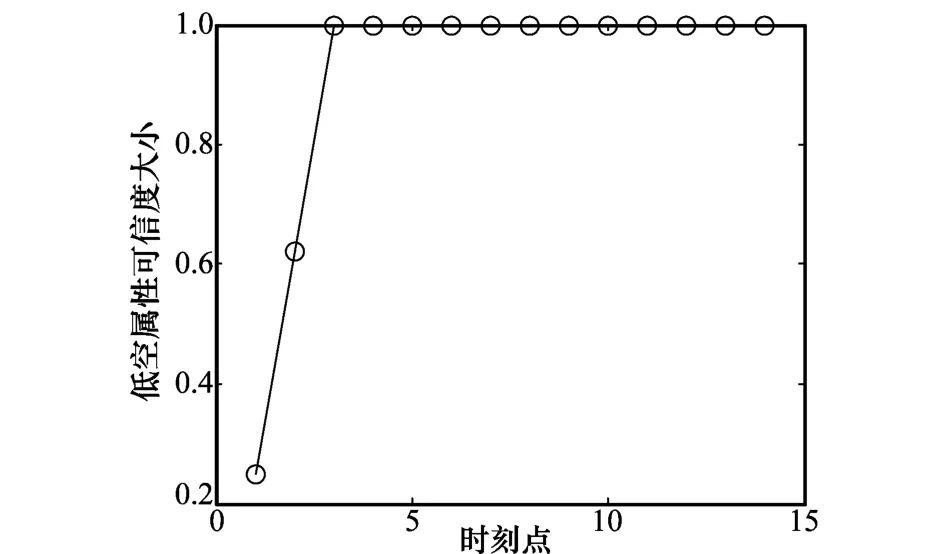
图4 目标低空属性可信度

由图4可见，本文提出的高度属性判别算法可以准确地判别低空飞行目标的高度属性。判别速度较快，只需要3个量测点迹信息就可以对目标高度属性进行正确判别，且目标高度属性判别可信度为1。

第2批次低空目标飞行高度为900 m，相对于观测站的方位角为14.8°。目标相对于观测站的航迹如图5所示，高度属性判别结果如图6所示。

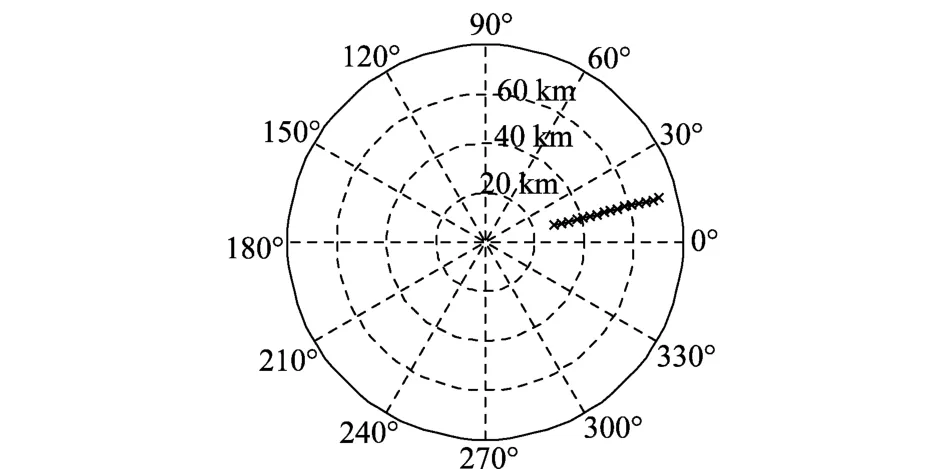
图5 目标相对于观测站航迹

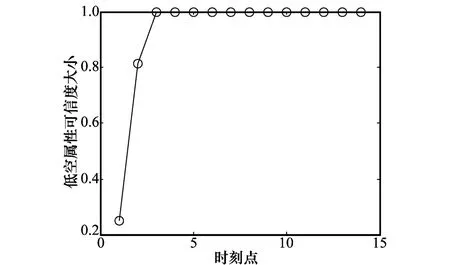
图6 目标低空属性可信度大小

由图6可见，在目标飞行高度为900 m的情况下，在4个量测点迹时间内仍然可以正确判别出目标高度属性，判别速度快。

以上分析了低空目标的高度属性判别，并得到了精确的判别结果。以下部分将验证高空飞行目标的飞行高度属性判别，该目标为非合作民航目标，高度信息未知，采用文献［10］提出的方法估计目标高度。

第3批飞行目标为高空飞行民航目标，其相对于雷达观测站的航迹如图7所示，目标飞行高度估计和高度属性判别可信度分别如图8和图9所示。该民航目标飞往韩国、日本方向，目标高度估计高度为11 km，航向速度为938.9 km／h。一般国际民航飞机飞行高度为10.7 km左右，高度估计结果为11 km与经验值相符合，且高空属性判别可信度达到0.95左右。因此，以上飞行高度和属性判别结果验证了本文提出的高度属性判别算法的有效性和正确性。

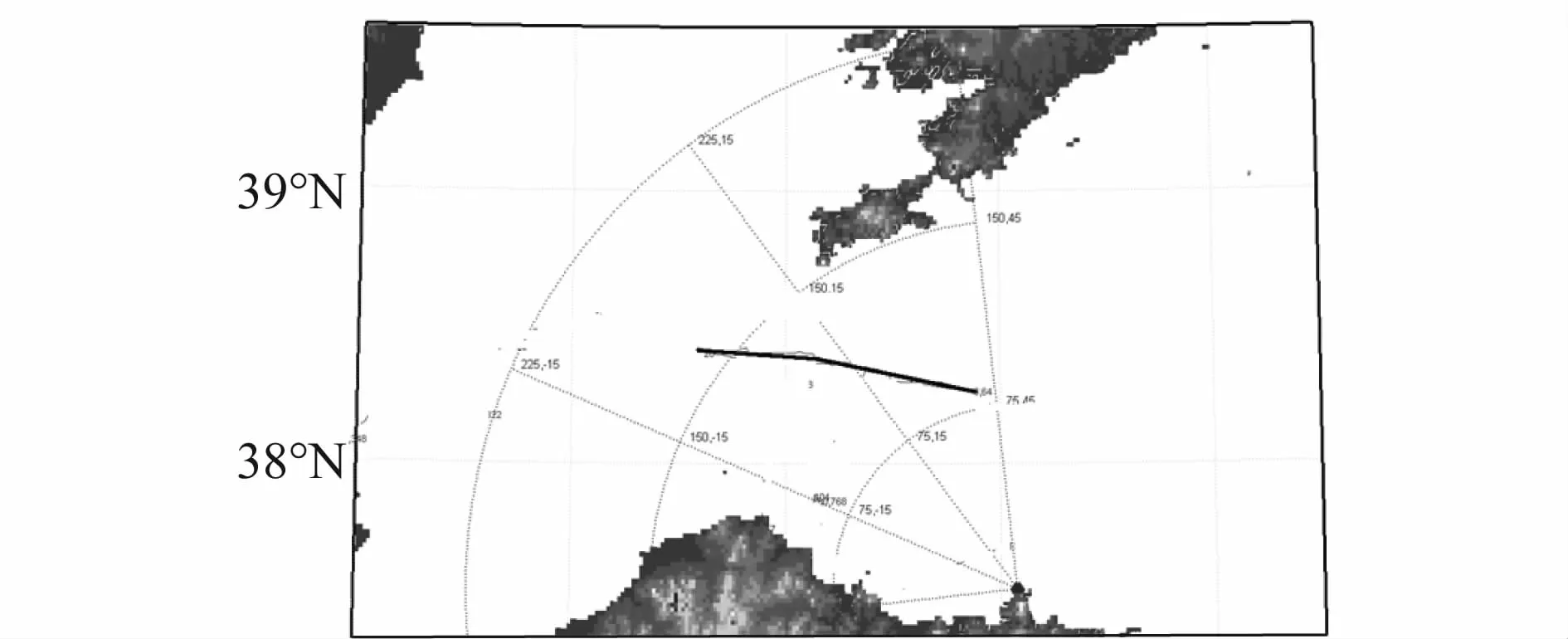
图7 目标航迹

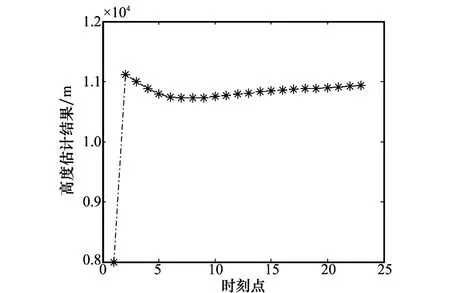
图8 高度估计结果

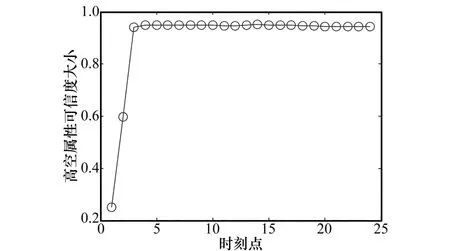
图9 高空属性判别可信度

第4批次目标飞行航迹如图10所示，航迹图中粗线为要处理的非合作民航目标。其高度估计结果和目标高度属性判别结果如图11和图12所示。

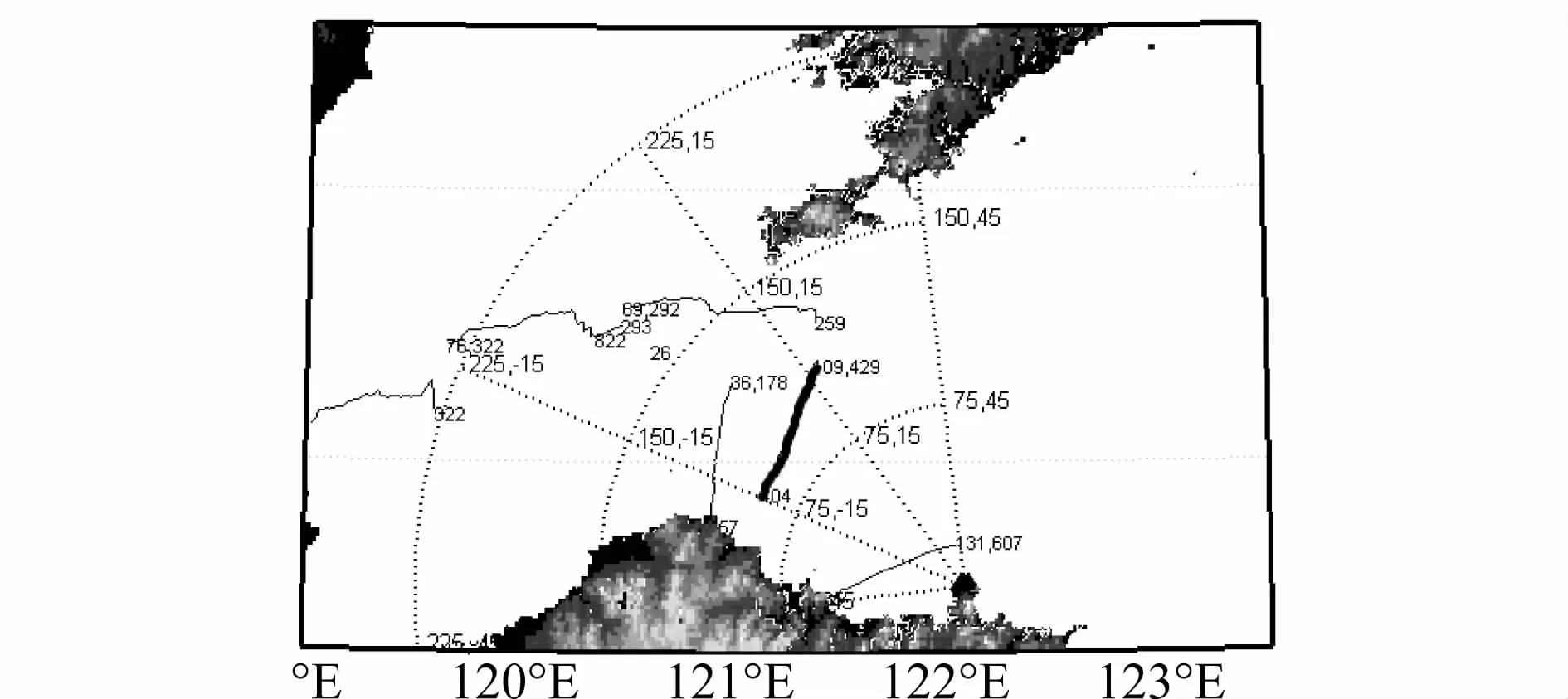
图10 目标航迹

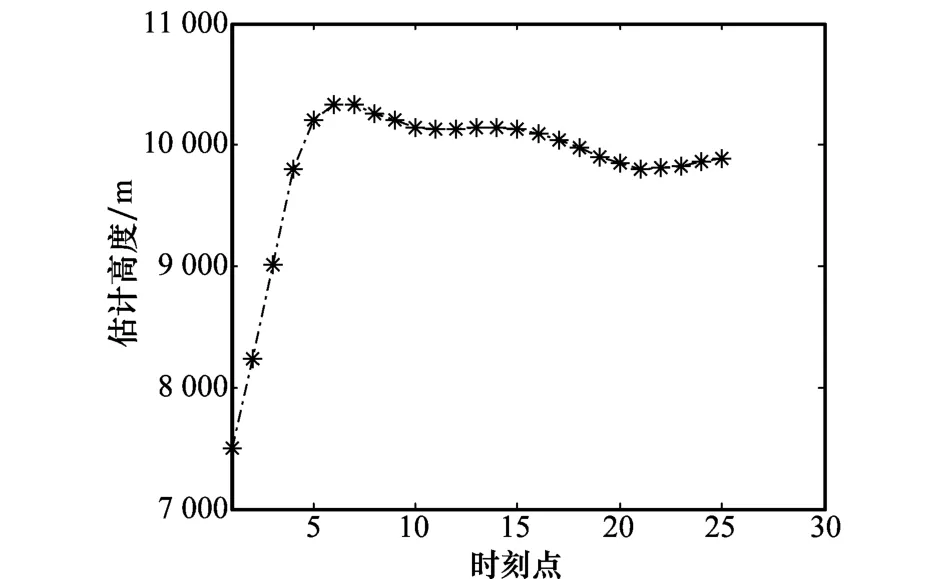
图11 高度估计结果

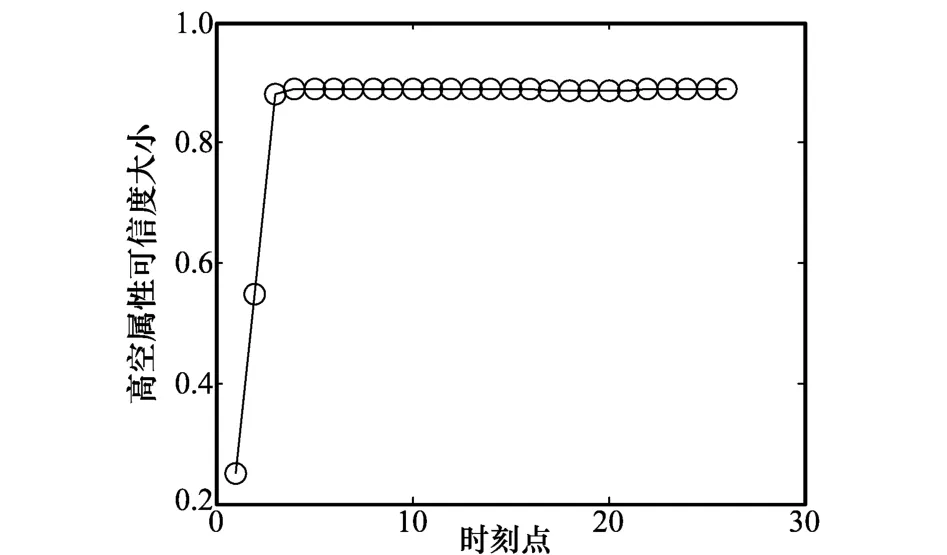
图12 高空属性判别可信度

由图11可见，目标高度估计结果为9.7 km左右，图12所示的高度属性判别可信度显示目标为高空属性，属性判别正确，高空属性可信度为90%。从图10所示的目标航迹可见，目标从山东飞往大连方向，航向速度为730 km／h。根据经验可知，国内民航飞机一般为波音737类型中型飞机，飞行高度在9 km左右。因此，本试验结果表明，高度估计误差在10%左右，目标高度属性判别正确。

4 结论

本文利用垂直极化电波在高空和低空高度范围内的传播衰减的不同特性，提出一种基于信号回波强度信息的目标高度属性判别算法，首次解决了HFSWR飞行目标高度属性判别问题。这种属性判别算法不仅判别目标高度属性，而且给出了高度属性判别可信度。实测数据处理表明，本算法能够在5个观测时间内判别出目标高度属性，属性判别可信度达到90%。

［1］Anderson S J.Optimizing HF radar siting for surveillance and remote sensing in the Strait of Malacca［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（3）：1805-1816.

［2］Xie J，Sun M，Ji Z.First-order ocean surface cross section for shipborne HFSWR［J］.Electronics Letters，2013，49（16）：1025 -1026.

［3］Zhou H，Wen B，Wu S.Ionospheric clutter suppression in HFSWR using multilayer crossed-loop antennas［J］.IEEE Geoscience and Remote Sensing Letters，2014，11（2），429-433.

［4］Grosdidier S，Forget P，Barbin Y，et al.HF bistatic ocean doppler spectra：simulation versus experimentation［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，52（4），2138-2148.

［5］Bruno L，Braca P，Horstmann J，et al.Experimental evaluation of the range doppler coupling on HF surface wave radars［J］.IEEE Geoscience and Remote Sensing Letters，2013，10（4）：850-854.

［6］Sathyan T，Chin T J，Arulampalam S，et al.A multiple hypothesis tracker for multitarget tracking with multiple simultaneous measurements［J］.IEEE Journal of Selected Topics in Signal Processing，2013，7（2）：448-460.

［7］Abramovich Y I，Frazer G J，Johnson B A.Principles of mode selective MIMO OTHR［J］.IEEE Trans.on Aerospace and Electronic Systems，2013，49（3）：1839-1868.

［8］Skolnik M I.Introduction to radar system［M］.3rd ed.Zhuo Q S trans.Beijing：Publishing House of Electronics Industry，2006：392-393.（Skolnik M I.雷达系统导论［M］.3版.左群声，译.北京：电子工业出版社，2006：392-393.）

［9］Howland P E，Clutterbuck C F.Estimation of target altitude in HF surface wave radar［C］∥Proc.of the 7th International Conference on HF Radio Systems and Techniques，1997：296-300.

［10］Zhang S，Jin Y G，Yu C J.HPEKF algorithm of target altitude estimation initializing in HF surface wave radar［J］.Journal of Harbin Institute of Technology，2007，39（5）：726-729.（张硕，金永镐，于长军.高频地波雷达目标高度估计起始的HPEKF算法［J］.哈尔滨工业大学学报，2007，39（5）：725-729.）

［11］Gai M J，Yi X，He Y，et al.An approach to tracking a 3D-target with 2D-Radar［C］∥Proc.of IEEE International Radar Conference，2005：763-768.

［12］Guo R J，Yuan Y S，Quan T F.Study of anti-weak aerial target tracking for high Frequency surface wave radar［J］.Acta Electronica Sinica，2005，16（2）：1586-1589.（郭汝江，袁业术，权太范.高频地波雷达飞行小目标跟踪方法研究［J］.电子学报，2005，16（2）：1586-1589.）

［13］Rotheram S.Ground-wave propagation.Part 1：Theory for short distances［J］.IEE Communications Radar and Signal Processing，1981，128（5）：275-284.

［14］Rotheram S.Ground-wave propagation.Part 2：Theory for short distances［J］.IEE Communications Radar and Signal Processing，1981，128（5）：285-295.

Target flight mode identification with HFSWR

ZHAO Kong-rui1，YU Chang-jun2，LIU Ai-jun2，JIAN Wei-le2，QUAN Tai-fan2
（1.School of Electronics and Information Engineering，Harbin Institute of Technology，Harbin 150001，China；2.School of Information and Electrical Engineering，Harbin Institute of Technology（Weihai），Weihai 264209，China）

Fight altitude estimation of aircraft is a hotspot in high frequency surface wave radar（HFSWR）application which has not been resolved effectively.However，it is more meaningful and available to identify the flight mode of aircraft than cost too much time to estimate the target altitude in the engineering application.Based on the above viewpiont，an engineering method is proposed to solve the flight mode identification problem with the variation property of the propagation attenuation at different altitude intervals.This method can identify the target flight mode and evaluate the probability of the flight mode.Practical trials demonstrate that the proposed method can identifiy the target flight mode with a small quantity of measurement data，the aircraft flight mode can be identified correctly and the identification probability achieves more than 90%.

high frequency surface wave radar（HFSWR）；flight mode；propagation attenuation

TN 959.72 文献标志码：A DOI：10.3969／j.issn.1001-506X.2015.09.10

赵孔瑞（1984-），男，博士，主要研究方向为高频地波雷达信号处理。

E-mail：zhaokongrui＠163.com

于长军（1962-），男，教授，博士，主要研究方向为雷达系统及信号处理。

E-mail：yuchangjun＠hit.edu.cn

刘爱军（1971-），男，副教授，博士，主要研究方向为雷达信号处理与通信系统。

E-mail：hitlaj＠163.com

菅维乐（1978-），男，讲师，主要研究方向为雷达信号处理。

E-mail：jianweile＠sina.com

权太范（1949-），男，教授，主要研究方向为高频地波雷达信号处理、数据处理及多源信息融合。

E-mail：quantaif＠hit.edu.cn