基于自适应混合能量参数的变步长LMS水声信道均衡算法

2015-07-26宁小玲张林森刘志坤

系统工程与电子技术 2015年9期

关键词：水声步长稳态

宁小玲，张林森，刘志坤

（1.海军工程大学电子工程学院，湖北武汉430033；2.海军工程大学兵器工程系，湖北武汉430033）

基于自适应混合能量参数的变步长LMS水声信道均衡算法

宁小玲1，张林森2，刘志坤1

（1.海军工程大学电子工程学院，湖北武汉430033；2.海军工程大学兵器工程系，湖北武汉430033）

提出了一种新的变步长算法，并将该算法用于水声信道均衡。该算法克服改进归一化最小均方（developed normanized least mean square，XENLMS）算法依赖固定能量参数λ的局限性，遵循变步长算法的步长调整原则在XENLMS算法的基础上引入一个自适应混合能量参数λk，改善算法收敛速度和鲁棒性。首先通过仿真分析变步长算法中的3个固定参数α，β，μ的取值范围及对算法收敛性能的影响；并在两种典型的水声信道环境下，采用两种调制信号对算法的收敛性能进行计算机仿真，结果显示，新算法的收敛速度明显快于XENLMS算法和已有的变步长算法，收敛性能接近递归最小二乘（recursive least square，RLS）算法的最优性能，但计算复杂度远小于RLS算法。最后，木兰湖试验验证了带判决反馈均衡器（decision feedback equalization，DFE）结构的新算法具有较好的克服多径效应和多普勒频移补偿的能力，相比LMS-DFE提高了一个数量级。

最小均方算法；变步长；收敛速度；稳态误差；信道均衡；水声通信

0 引言

自适应均衡技术都可以有效地消除码间干扰，补偿信道的畸变，利用自适应均衡技术来提高水声通信系统的传输速率和频带利用率，己经成为现阶段水声通信系统的特征之一［1］。最小均方（least mean square，LMS）算法因其低的计算复杂度、在平稳环境中的收敛性及易于硬件实现等主要特征，是自适应滤波理论中应用最广泛的算法，并在相干水声通信中被普遍应用［2］：文献［3］提出了一种基于判决反馈结构的LMS算法，并通过水池试验检验了算法的收敛性能。文献［4］提出了一种改进的归一化LMS算法（generalized normalized gradient descent regularization normanized LMS，GNGD-NLMS），提高了跟踪信道的能力。但LMS算法对步长非常敏感，为了克服这个问题，文献［5］将快速自优化LMS分集合并算法（fast self-optimized LMS diversity combiner，FOLMSDC）、快速自优化LMS算法（fast self-optimized LMS，FOLMS）和快速自优化LMS相位补偿算法（fast self-optimized LMS phase compensation，FOLMSPC）有机地结合在一起，按照最小化均方误差准则调节各部分的系数，从而实现均衡器性能的全局最优。由于高速水声通信时的信道响应较长，水声信道呈现出稀疏性，针对这个问题，文献［6］采用了基于LMS算法的稀疏迭代方法，有效降低了计算量。文献［7］提出了一种对滤波器输入向量X（k）和误差e（k）进行归一化的LMS算法（developed normanized least mean square，XENLMS），该算法在水声信道环境下具有非常快的收敛速度。文献［8］提出了改进的系数比例稀疏信道自适应算法，并将改进的系数比例归一化LMS算法（improved proportionate normalized LMS，IPNLMS）、改进的比例仿射投影算法（improved proportionate affine projection algorithm，IPAPA）、NLMS算法以及RLS算法进比较，将这几种算法用于水声信道估计和均衡。

LMS算法的优势是显而易见的，但是收敛速度慢，收敛速度与自适应步长和稳态失调之间存在矛盾。为克服这一缺点，多种不同的改进方法得到研究，这些方法性能的提高大部分是通过改变步长实现的［915］。为了进一步优化算法，提高收敛速度，本文提出了一种基于自适应混合能量参数的变步长LMS水声信道均衡算法，并分别从仿真分析和湖泊实验对算法的性能进行验证。

1 新的变步长LMS算法

LMS算法因其低的计算复杂度、在平稳环境中的收敛性以及易于硬件实现等主要特征，目前是自适应滤波理论中应用最广泛的算法。图1是LMS用于自适应均衡的基带模型。

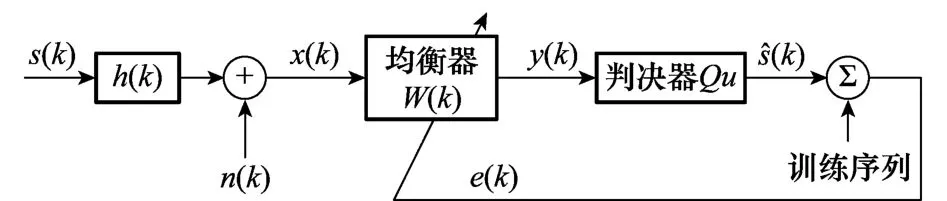
图1 自适应均衡算法的基带模型图

图中，s（k）是信源发送的均值为零的独立同分布基带时域信号，h（k）是基带水声信道冲激响应，n（k）是高斯噪声，滤波器输入信号x（k）＝h（k）⊗s（k）+n（k），文献［7］对滤波器输入向量X（k）和误差e（k）进行归一化得到XENLMS算法，权值迭代方程为

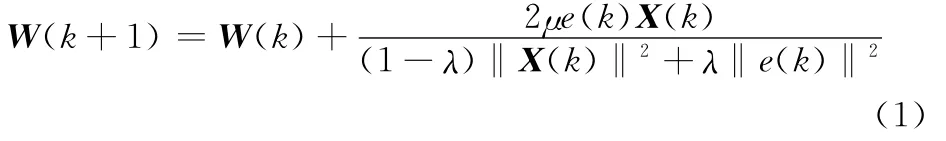
式中，W（k）＝［w0（k） w1（k） … wN－1（k）］T是滤波器权值向量；X（k）＝［x（k） x（k－1） … x（k－N+1）］T是滤波器输入向量，N是均衡滤波器的长度；λ是混合能量参数；‖X（k）‖2表示滤波器输入向量X（k）欧几里得范数的平方，计算公式为‖X（k）‖2＝XT（k）X（k）；ˆs（k）代表量化判决器Qu的输出。

在式（1）中，XENLMS算法被输入信号能量和误差信号能量归一化，有效地改善了稳定性和收敛速度。但是，混合能量参数λ需要在收敛速度和低稳态误差之间折中选取，而且XENLMS算法通过一个固定的混合能量参数进行权值迭代，算法的性能依赖这个混合参数的选择。

因此，为了有效地改善收敛性能，需要引进一个自适应变化的混合能量参数λk，使算法在初始收敛阶段能够选择较大的步长，以达到快速收敛；随着权向量接近最优解，能够逐步减小步长以保证进一步收敛，从而减小稳态误差。这种变化的混合能量参数使XENLMS算法克服了自适应稳态阶段步长调整过程中的不足，具有快速收敛性能和良好的鲁棒性。

首先，对误差量的前后时刻采样进行相关，其更新方程为

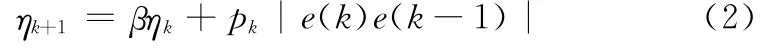
式中，e（k）e（k－1）确定W（k）与最优权值的距离；β是一个常数；pk由λk的过去两个采样加权和进行更新，即

式中，α是一个常数，这样可以更加灵活地得到控制ηk的递归曲线。e（k）和e（k－1）之间的自相关估计被用作控制混合能量参数λk，即

这样，通过引进自适应变步长的混合能量参数λk，得到的变步长LMS算法（variable step size XENLMS，VSS-XENLMS）的权值迭代方程为

算法中测量误差为

式中，d（k）是理想输出。

滤波器输出为

2 算法性能比较与分析

2.1 新算法的收敛性能分析

论文提出的新算法中关于步长的迭代有3个常数α、β、μ，将α和β分为一组，变化α、β与μ这两组参数，并分析其变化对算法收敛性能的影响。

仿真初始条件：信噪比为20 dB，四相相移键控（quadrature phase shift keying，QPSK）调制信号，水声信道模型采用典型的带相位旋转的稀疏两径水声信道h1＝［e－0.7j，0，0，e－1.8j］［16］，各均衡器抽头个数取M＝32。

（1）变化μ初始值。取α＝β＝0.2，当μ的值分别取μ1＝0.02，μ2＝0.08，μ3＝0.2，μ4＝0.5时，本文算法均方误差曲线的变化趋势如图2（a）所示，从图2（a）可以看出，新算法的收敛速度随步长μ逐步增大而逐渐增快，且变化明显。当收敛稳定时，算法的稳定误差均在－15 dB左右。

图2 本文算法均方误差曲线的变化趋势

（2）变化α和β初始值。分别取大步长μ＝0.2和小步长μ＝0.02，当α和β的值分别取α1＝β1＝0.05，α2＝β2＝0.3，α3＝β3＝0.5时，得到的均方误差收敛曲线如图2（b）所示。可以看出，当取两个相差比较大的步长μ时，改变α和β值，收敛曲线的变化趋势是相同的：随着α和β逐步增大，算法的收敛速度逐渐增快。且仿真过程中发现，当步长α和β初始值超过0.5时，算法收敛不稳定。所以，在本文的仿真条件下，β最佳值为0.5。

（3）经过仿真发现，满足当步长α和β初始值超过0.5时，μ的取值范围为μ∈（0，1］。

2.2 与XENLMS和RLS算法的比较

即使在输入信号相关矩阵的特征值扩展比较大的情况下，RLS算法都能实现快速收敛，但其实现是以增加计算复杂度和稳定性问题为代价。由于XENLMS算法对输入信号能量和误差信号能量归一化，有效地改善了稳定性和收敛速度，所以，本文对RLS、XENLMS以及本文提出的VSS-XENLMS 3种算法比较其收敛性能。

仿真初始条件：信噪比为20 dB，调制信号分别采用QPSK和16进制的正交振幅调制（16 quadrature amplitude modulation，16QAM）信号，采用2种水声信道模型，信道1为h1＝［e－0.7j，0，0，e－1.8j］，均衡器抽头个数取M＝32，信道2为稀疏多径信道H2（z）＝1－0.5z－14+0.4z－18［7］，相比信道1复杂，均衡器抽头个数取M＝82。

仿真中各算法的参数选取：

XENLMS算法：μ＝0.5，λ＝0.05；

VSS-XENLMS算法：μ＝0.5，α3＝0.3，β3＝0.3；

RLS算法：指数加权因子ω＝1（最优因子），取此参数时RLS算法具有最优性能。

仿真结果如图3所示。

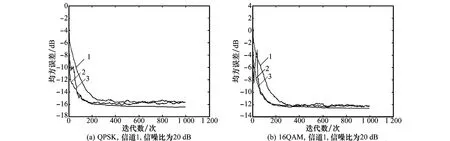
图3 两种调制方式下的3种算法的收敛曲线比较

从图3（a）可知，在信道1和QPSK调制的仿真条件下，XENLMS算法的收敛速度慢于VSS-XENLMS算法，约慢100次迭代，收敛后的稳态误差相差无几；VSS-XENLMS算法相比RLS算法在初始收敛和收敛稳定后的收敛速度都相差不大，但收敛初始阶段，RLS算法由于递归计算积累，对舍入误差非常敏感，而VSS-XENLMS算法的收敛曲线平滑，收敛后VSS-XENLMS算法的稳态误差约高出1 dB。图3（b）与图3（a）相比，3种算法的收敛趋势完全相同，变化的是在使用16QAM调制信号初始条件下，收敛稳定后各算法的稳态误差与使用QPSK调制信号时得到的稳态误差相比增大了约4 dB。

水声信道模型由信道1变为信道2，图3（c）中3种算法的收敛曲线与图3（a）相比有所变化：XENLMS算法、VSS-XENLMS算法及RLS算法的收敛速度依次增强，VSS-XENLMS算法收敛速度快于XENLMS算法，大约快300次迭代，收敛后的稳态误差相差无几；RLS算法与VSS-XENLMS算法差不多同时收敛稳定（相差约100次迭代），收敛后的稳态误差相差无几。同样，由于信道环境改变，图3（d）与图3（b）之间的差异与图3（c）和图3（a）相近，图3（d）与图3（b）收敛后的稳态误差相差约6 dB。

由以上比较可得出，分别在两种调制信号和复杂度不同的水声信道环境下，VSS-XENLMS算法依然保持和RLS算法的性能相当，但VSS-XENLMS算法的计算复杂度远小于RLS算法，综合各种因素，VSS-XENLMS算法是一种理想的自适应滤波均衡算法。

2.3 与其他变步长算法的比较

文献［12］基于文献［17］给出了一种新的基于Sigmoid函数的变步长LMS算法，改善了算法的收敛性能，并减小了计算量。文献［13］也给出了相应的改进变步长算法，改善了算法性能。文献［14］提出了以改进双曲正切函数为变步长的LMS算法，在相同的实验条件下优于以上算法。本文将文献［14］的变步长和XENLMS算法相结合，其权值迭代函数为

基于文献［14］的变步长XENLMS算法的仿真参数采用文献［14］的最优参数：β＝0.2，α＝80，h＝2 000，为了合理比较，本论文新算法的参数μ与文献［14］中相应的参数β相同：μ＝0.2（从图2看出非最优参数），得到的收敛性能曲线如图4所示。

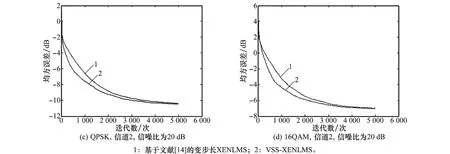
图4 本文算法（VSS-XENLMS）和基于文献［14］的变步长XENLMS算法收敛曲线比较

由图4（a）可以看出，两算法最终的稳态误差一致，约－16 dB；在开始收敛阶段，两者的收敛速度相差不大；接近稳定时，本论文算法收敛加快，到达稳定时，本论文算法相比基于文献［14］的变步长XENLMS算法收敛速度快，约快400次迭代。由图4（b）可以看出，两算法最终的稳态误差约－12 d B；在开始收敛阶段，本论文算法的收敛速度明显快于基于文献［14］的变步长XENLMS算法；到达稳定时，本论文算法收敛速度快，约快300次迭代。图4（c）和图4（d）的收敛趋势一致：到达收敛稳定时，两算法的收敛速度差300次迭代。

可见，本论文算法在不同调制信号和不同信道环境的仿真条件下，性能均优于基于文献［14］的变步长XENLMS算法，是一种快速收敛的自适应变步长均衡算法。

2.4 湖泊实验

武汉木兰湖的水声实验对以上的自适应均衡算法性能进行了检验，实验布局如图5所示。实验当天下有小雨，风力较强，湖面波浪明显，周围环境较为安静，发射端与接收端分别放置于水下6 m和5 m处，水平间距330 m，由于船体剧烈摇摆，带动发射换能器和接收水听器剧烈运动。

图5 水声通信实验布局图

实验中采用判决反馈均衡器结构，Mi、Mb分别为前馈、反馈滤波器阶数，Mi＝101，Mb＝50。实验中各算法的参数如下：LMS-DFE：μi＝0.000 5，μb＝0.000 5； XENLMS-DFE算法：μi＝0.2，λ＝0.005，μb＝0.0015；文献［14］的变步长XENLMS-DFE算法：β＝0.2，α＝80，h＝2 000；VSS-XENLMS-DFE：μ＝0.5，α＝0.3，β＝0.3。

在木兰湖实地测得的时变水声信道通信带宽内（加窗处理，通带范围12.25～14.75 KHz）的功率谱（自动增益控制补偿后的结果）如图6所示。由图6可见，在木兰湖中，带内功率谱发生明显的起伏，水声信道多径效应是造成这种起伏的重要原因之一，对通信信号造成了很大干扰，这些都与实际实验环境相符合。图7为各种均衡算法的效果图。

图6 实验环境下的带内功率谱

从图7可以看出，LMS-DFE、XENLMS-DFE、基于文献［14］的XENLMS-DFE以及VSS-XENLMS-DFE各算法的星座图逐渐清晰：LMS-DFE算法的性能较差，误码率为0.39%，星座图较混乱；XENLMS-DFE算法误码率为0.16%，星座图界限分明，清晰一些；基于文献［14］的XENLMS-DFE算法误码率为0.081 25%，星座图更加清晰；VSS-XENLMS-DFE算法误码率为0.031 2%，星座图紧凑集中，界限分明，清晰很多，误码率相比LMS-DFE算法提高了一个数量级。

图7 木兰湖实验——距离330 m（QPSK）

3 结论

通过建立混合能量参数λ与误差信号的另一种非线性函数关系：λk＝erf（ηk），ηk+1＝βηk+pk｜e（k）e（k－1）｜，pk＝α（λk+λk－1），提出了一种新的变步长自适应均衡算法。分析了参数α、β及μ对算法收敛性能的影响以及在本文的仿真环境下的取值范围。在复杂度不同的调制信号和信道环境中，该算法均表现出较好的收敛性能，收敛速度快于XENLMS算法，与RLS收敛后的稳态误差相同，收敛速度也相差甚微，且新算法的收敛性能比基于文献［14］的变步长XENLMS算法要优越。最后，采用判决反馈均衡器结构进行了湖试试验，比较了各算法的输出星座和误码率，本论文的VSS-XENLMS-DFE算法相比LMS-DFE提高了一个数量级。

［1］Kilfoyle D B，Baggeroer A B.The state of the art in underwater acoustic telemeiry［J］.IEEE Journal of Oceanic Engineering，2000，25（1）：4-27.

［2］Istepanion R S H，Stojanovic M.Under-water acoustic digital signal processing and communication systems［M］.London：Kluwer Academic publishers，2002：4-16.

［3］Goalic A.Toward a digital acoustic underwater phone［C］∥Proc.of the Marine Technology Society／IEEE Oceans Conference，1994：489-494.

［4］Abdaoui A，Laot C.Blind DFE based on NLMS algorithm with generalized normalized gradient descent regularization［C］∥Proc.of the Oceans，Marine Technology Society／IEEE Biloxi-Marine Technology for Our Future：Global and Local Challenges，2009：123-127.

［5］Zhao L，Zhu W Q，Zhu M.An adaptive equalization algorithm for underwater acoustic coherent communication system［J］.Journal of Electronics&Information Technology，2008，30（3）：648-651.（赵亮，朱维庆，朱敏.一种用于水声相干通信系统的自适应均衡算法［J］.电子与信息学报，2008，30（3）：648-651.）

［6］Geller B，Capellano V，Jourdain G.Equalizer for real time high rate transmission in underwater communications［C］∥Proc.of the International Conference on Acoustics，Speech，and Signal Processing，1995：3179-3182.

［7］Ning X L，Liu Z，Luo Y S，et al.Fast convergence adaptive equalization algorithm for underwater acoustic channels［J］.Systems Engineering and Electronics，2010，32（12）：2524-2527.（宁小玲，刘忠，罗亚松，等.水声信道快速收敛自适应算法［J］.系统工程与电子技术，2010，32（12）：2524-2527.）

［8］Pelekanakis K，Chitre M.Comparison of sparse adaptive filters for underwater acoustic channel equalization／estimation［C］∥Proc.of the IEEE International Conference on Communication Systems，2010：395-399.［9］Gupta A，Joshi S.Variable step-size LMS algorithm for fractal signals［J］.IEEE Trans.on Signal Processing，2008，56（4）：1411-1420.

［10］Zhao S，Man Z，Khoo S，et al.Variable step-size LMS algorithm

with a quotient form［J］.Signal Processing，2009，89（1）：67-76.［11］Zerguine A，Chan M K，Al-Naffouri T Y，et al.Convergence and

tracking analysis of avariable normalised LMF（XE-NLMF）algorithm［J］.Signal Processing，2010，89：778-790.

［12］Gao Y，Xie S L.A variable step size LMS adaptive filtering algorithm and it s analysis［J］.Acta Electronica Sinica，2001，9（8）：1094-097.（高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29（8）：1094-1096.）

［13］Luo X D，Jia Z H，Wang Q.A new variable step size LMS adaptive filtering algorithm［J］.Acta Electronica Sinica，2006，34（6）：1123-1126.（罗小东，贾振红，王强.一种新的变步长LMS自适应滤波算法［J］.电子学报，2006，34（6）：1123-1126.）

［14］Zhang Z H，Zhang D J.New variable step size LMS adaptive filtering algorithm and its performance analysis［J］.Systems Engineering and Electronics，2009，31（9）：2238-2241.（张中华，张端金.一种新的变步长LMS自适应滤波算法及性能分析［J］.系统工程与电子技术，2009，31（9）：2238-2241.）

［15］Fu X Z，Liu Z，Li C X.Anti-interference performance improvement for sigmoid function variable step-size LMSadaptive algorithm［J］.Journal of Beijing University of Posts and Telecommunications，2011，34（6）：112-120.（付学志，刘忠，李朝旭.Sigmoid函数变步长LMS自适应算法的抗干扰性能改进［J］.北京邮电大学学报，2011，34（6）：112-120.）

［16］Falahati A，Woodward B，Bateman S C.Underwater acoustic channel models for 4800b／s QPSK signals［J］.IEEE Journal of Oceanic Engineering，1991，16（1）：12-19.

［17］Qin J F，Ouyang J Z.A new variable step size LMS adaptive filtering algorithm［J］.Data Acquisition and Processing，1997，12（3）：171-174.（覃景繁，欧阳景正.一种新的变步长LMS自适应滤波算法［J］.数据采集与处理，1997，12（3）：171-174.）

Variable step size LMSequalization algorithm based on adaptive mixed-power parameter in underwater acoustic channels

NING Xiao-ling1，ZHANG Lin-sen2，LIU Zhi-kun1
（1.Electronics Engineering College，Naval University of Engineering，Wuhan 430033，China；2.Department of Weaponry Engineering，Naval University of Engineering，Wuhan 430033，China）

An improved novel variable step size least mean square（VSS-XENLMS）adaptive filtering algorithm is proposed and it is applied to underwater acoustic equalization.A variable mixed-power parameterλkis introduced whose the time variation allows the algorithm to follow fast changes in the channel.The proposed algorithm overcomes the dependency on the selection of the mixing parameterλ，which has been by developed normanized least mean square（XENLMS）algorithm.The selecting about three factorsα，βandμand their influences to convergence ability are analysed.Computer simulations of the proposed algorithm about convergence ability are carried out respectively under two underwater acoustic channels，using two modulation signals.Simulation results demonstrate that the convergence speed of the proposed algorithm compared with that of XENLMS algorithm and the former variable step-size algorithms has been visibly increased，the convergence performance of the proposed algorithm is compared to that of recursive least square（RLS），but its computation complexity is far less RLS.Then，Mulan Lake experiment shows that the performance of the decision feedback equalization（DFE）-based the proposed algorithm（VSS-XENLMS-DFE）is better than that of the LMS-DFE algorithm in terms of bit error rate for an order of magnitude，which overcomes the effects of multipath and Doppler shift very well.

least mean square（LMS）algorithm；variable step size；convergence speed；steady-state error；channel equalization；underwater acoustic communication

TN 929.3 文献标志码：A DOI：10.3969／j.issn.1001-506X.2015.09.28

宁小玲（1982-），女，讲师，博士，主要研究方向为水下高速率数据通信、水声信道估计与均衡。

E-mail：zhang＿ning1982b＠sina.com

张林森（1982-），男，讲师，博士，主要研究方向为水下航行器推进控制技术研究。

E-mail：zhangk＠gmail.com.cn

刘志坤（1984-），男，讲师，博士，主要研究方向为水下高速率数据通信、目标定位与跟踪。

E-mail：bill1302lzk＠sina.com

1001-506X（2015）09-2141-07

2014-06-16；

2015-01-18；网络优先出版日期：2015-04-03。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150403.1021.001.html