运载火箭的抗干扰分数阶控制器设计

程昊宇，董朝阳，王 青

（1.北京航空航天大学航空科学与工程学院，北京100191；2.北京航空航天大学自动化科学与电气工程学院，北京100191）

运载火箭的抗干扰分数阶控制器设计

程昊宇1，董朝阳1，王 青2

（1.北京航空航天大学航空科学与工程学院，北京100191；2.北京航空航天大学自动化科学与电气工程学院，北京100191）

针对火箭的姿态控制问题，基于自抗扰理论和分数阶控制，提出了一种控制器设计方法。通过设计扩张状态观测器，充分利用惯组平台和速率陀螺的复合量测信息对系统的内部和外部干扰进行估计。设计分数阶控制器对估计的干扰进行实时补偿，实现火箭的姿态控制，通过引入可调参数使得控制器参数调整范围变大，保证控制器具有更好的控制精度。考虑到控制器参数多且难以被确定，采用一种基于遗传算法和粒子群优化的混合算法对参数进行调整；通过仿真验证了所提算法可以获得良好的动态性能、抗扰性和鲁棒性。

姿态控制；扩张状态观测器；分数阶控制器；遗传算法；粒子群优化

0 引 言

随着空间发射任务的多样化和复杂化，运载火箭的结构越来越复杂，性能要求也越来越高。传统运载火箭采用比例微分+校正网络的控制方式［1］，对于不同的飞行状态，通过改变动静态增益和校正网络对火箭进行控制，但是运载火箭在飞行过程中会受到阵风等扰动的影响，导致姿态控制系统性能下降。传统比例微分（proportional-differential，PD）控制不易满足系统高性能的要求。为了满足运载火箭的机动性、灵活性以及卫星高精度入轨的要求，需要设计控制精度高、抗干扰能力强的姿态控制器。

近年来，许多学者对火箭的姿态控制进行了研究［2-4］，文献［3］采用自适应方法研究了火箭的姿态控制问题；文献［4］采用二阶滑模实现了运载火箭的姿态控制，在保证系统鲁棒性的前提下，有效地削弱了抖振现象。但是以上方法都依赖于火箭的精确模型，由于火箭模型复杂，在实际工程中很难获得精确的数学模型。分数阶PDμ控制［59］与滑模等现代控制方法相比，不仅具有传统PD控制不依赖于系统精确数学模型的优点，而且通过增加可调节参数扩大控制器的参数整定范围，与传统单纯调节动态增益和静态增益的控制方法相比，具有更好的控制效果和控制精度，可以很好地满足系统对控制精度和鲁棒性的要求［8］。

运载火箭在飞行过程中会受到各种内外不确定性的影响，这些不确定性会影响运载火箭的控制器性能甚至导致失稳，因此有必要研究对内外不确定性具有强鲁棒性的控制方法。自抗扰控制［1014］可以实时估计和补偿系统内部不确定动态，具有不依赖于被控对象的精确模型、鲁棒性强、精度高和抗干扰能力强的优点，在航空航天领域获得了广泛的应用［15-19］，文献［15］研究了航天器的高度控制问题，将滑模控制与自抗扰控制结合起来设计控制器；文献［17］针对航天器动力学姿态控制问题，提出了一种二阶线性自抗扰控制方法，说明了自抗扰算法具有较强的鲁棒性和控制精度。

基于以上分析，本文针对存在内外不确定性的运载火箭模型，将分数阶控制和自抗扰控制结合起来，设计了自抗扰分数阶控制器。首先，通过扩张状态观测器（extended state observer，ESO）对系统存在的内外不确定项进行实时估计。接着结合分数阶PDμ控制，设计控制器对火箭进行控制并实时补偿干扰。考虑到分数阶控制参数多且难以被确定的问题，将粒子群算法和遗传算法结合起来，对参数进行优化［2023］，并通过改变惯性权值来提高算法收敛速度。通过仿真验证了所设计的控制方法具有较好的控制精度和较强的鲁棒性。

1 模型描述

火箭的姿态控制是通过俯仰、偏航和滚转3个控制通道分别实现对俯仰、偏航和滚转方向的姿态进行控制。由于正常飞行时火箭3个通道的耦合程度较小，工程上一般将运载火箭的3个通道视为解耦的，分别进行控制器的设计。以俯仰通道为例，姿态控制系统是由箭体、惯组平台、速率陀螺、控制器、校正网络和伺服机构组成闭环控制回路，为了提高控制系统的鲁棒性，本文在此基础上引入了扩张状态观测器，设计的火箭姿态控制回路如图1所示。

图1 火箭姿态控制系统结构图

在半速度坐标系中箭体的质心运动方程分量形式为

式中，m为火箭质量；V为火箭速度；θ为弹道倾角；σ为航迹偏航角；FXh、FYh、FZh为存在弹性形变情况下，作用在火箭箭体上所有外力之和在半速度坐标系X、Y、Z 3个坐标轴上的分量。

令箭体坐标系3个坐标轴为箭体的惯量主轴，由动量矩定理可得运载火箭在箭体系下的绕质心运动方程为

式中，JX1、JY1、JZ1分别为火箭箭体绕箭体系X轴、Y轴、Z轴的转动惯量；MX1、MY1、MZ1为存在弹性形变的情况下，作用在火箭箭体上的外力之和对质心的力矩；ωX1、ωY1、ωZ1为箭体绕质心转动角速度在箭体坐标系中的投影分量。

运载火箭在飞行过程中会产生弹性形变，引起弹性振动，其中，俯仰方向的弹性振动方程为

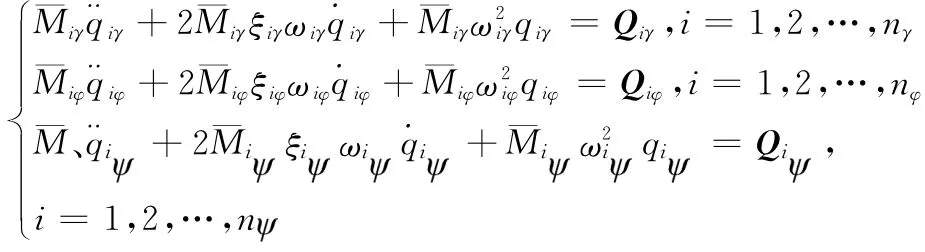
式中，ωiγ、ωiφ、ωi为滚转、俯仰、偏航方向第i阶振动圆频率；为对应方向第i阶阻尼比为相应的广义质量为相应的广义力为相应的广义坐标；nγ、nφ、n为各个方向弹性振动考虑的模态个数。

由于控制系统主要考虑的是姿态角偏差的消除，并使箭体按照选定的轨道和给定的程序角飞行，可以近似认为箭体姿态角偏差暂态过程中方程系数是固定不变的，可以采用“固化系数法”对火箭进行建模和分析。

本文以某型火箭俯仰通道为例进行姿态控制系统的设计，其刚体姿态运动方程［1］为

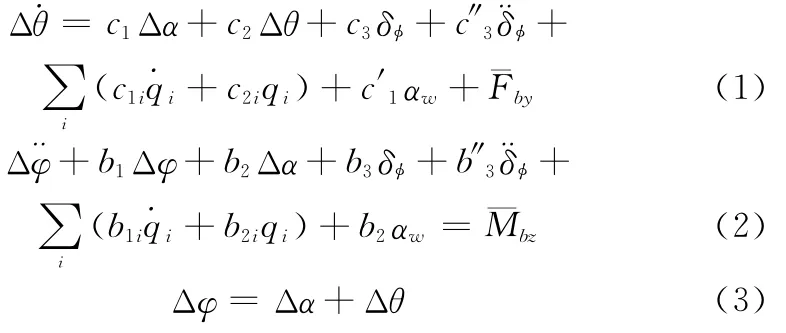
弹性振动方程为

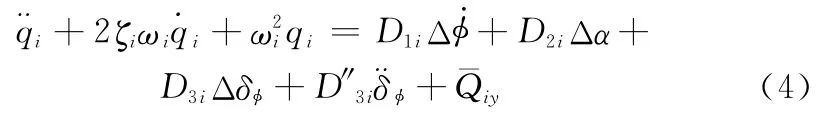
惯组平台和速率陀螺测量方程为

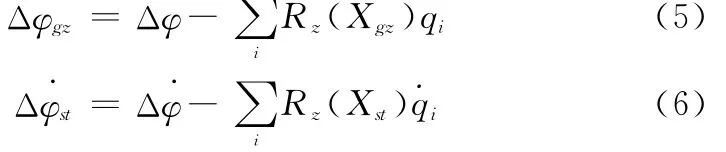
式中，Δθ为弹道倾角的偏差；Δα为箭体攻角的偏差；δφ为俯仰通道的发动机摆角输入为俯仰通道的发动机摆角加速度输入；αw为风攻角；为火箭受到的干扰力为火箭受到的干扰力矩； 为俯仰角的偏差； 和分Δφ Δφgz别为惯组平台和速率陀螺测量到的输出信号。

偏航通道控制器设计和滚动通道控制器设计与俯仰通道控制器设计类似，这里不再赘述。

2 扩张状态观测器设计

运载火箭在飞行过程中，会受到阵风、参数漂移等多种内外干扰的影响，柔性火箭的控制器设计还需要考虑箭体弹性振动的影响，而弹性振动频率也具有不确定性，这些不确定因素会使得姿态控制系统的稳定裕度降低，甚至失稳。本文综合利用惯组平台和速率陀螺的测量信息，设计扩张状态观测器，采用复合误差对姿态角、姿态角速度和内外干扰进行估计和补偿，简化了设计。定义复合观测误差为

式中，κ和λ为测量权重，可以调节来自惯组平台和速率陀螺两种测量信息的比例，若κ＝1，λ＝0，则退化为仅采用惯组平台测量信息的形式，若0＜κ＜1，0＜λ＜1，则表示综合采用惯组平台和速率陀螺的测量信息，可以通过改变权重，使得系统收敛速度加快，超调量减小。

设计扩张状态观测器为

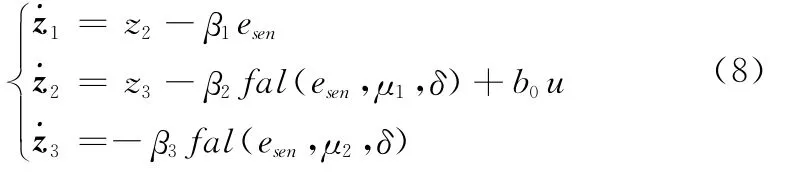
式中，z1、z2分别为俯仰角和俯仰角速率的估计；z3为内外不确定项的估计；β1、β2、β3为ESO的参数，可以根据观测效果进行调整；b0是决定补偿强弱的“补偿因子”，作为可调参数来使用；fal（·）为非线性函数；δ为设定值；μ1、μ2为其参数，可以根据误差大小来调整控制增益，其表达式为

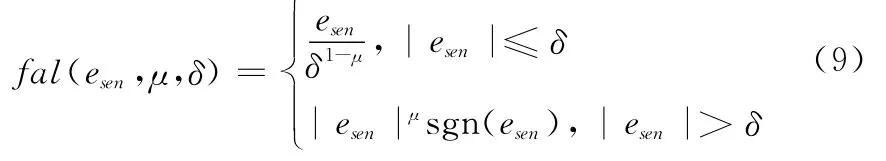
利用扩张状态观测器可以对系统中的扰动进行很好估计，然后反馈至控制器进行补偿。

3 分数阶控制器设计

分数阶微积分是将整数阶微积分拓展到实数域，通过引入可调算子，提高控制系统的控制效果和控制精度。其算子定义［89］为

式中，a和t分别为操作算子的上限和下限；α∈R为其阶次。

为了提高运载火箭姿态控制系统性能，采用分数阶PDμ控制器对运载火箭进行姿态控制，同时对扩张状态观测器的扰动估计值进行补偿，设计分数阶控制器为

由于分数阶控制器从理论上讲是无限维的，一般情况下不能直接对其进行分析和设计，需要将其转化为整数阶系统，用整数阶系统去近似分数阶系统，利用整数阶系统的分析方法对其进行分析和设计。本文采用文献［8］中提出的方法对其进行有理化近似，通过引入两个调整系数来提高拟合精度，在频率范围（ωb，ωh）内，将分数阶控制器转化为阶次为N的整数阶控制器，即

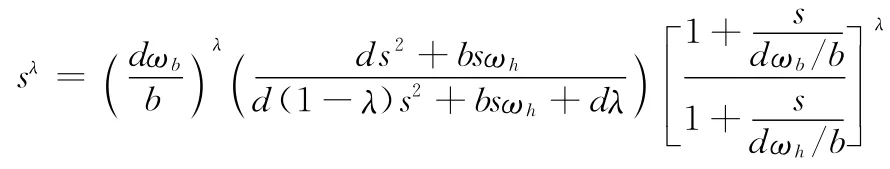
式中，b、d是为了提高频段两端拟合精度而引入的调整系数。将分数阶传递函数表示成整数阶传递函数的零极点形式为

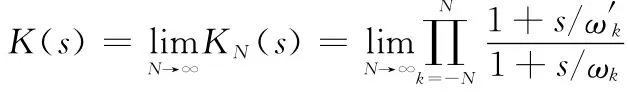
第k个零点、极点为

构造出分数阶微积分算子的连续有理传递函数模型为

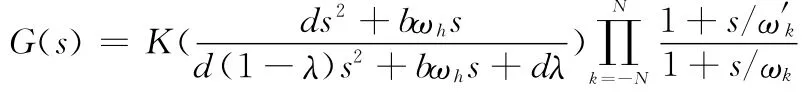
式中，K＝（ωbωh）α。

4 控制器参数优化设计

为了充分利用遗传算法较强的全局搜索能力和粒子群算法较快的收敛速度的优点，本文采用分层结构设计优化算法。底层采用遗传算法，对控制器参数进行全局搜索；然后选取遗传算法搜索得到的最优解作为顶层算法的初始种群，采用粒子群算法对控制器参数进行精确局部搜索，而且为了提高粒子群算法的收敛速度，采用动态惯性权值对算法进行设计。

本文对分数阶控制器和扩张状态观测器的参数进行优化，待优化参数为：①分数阶控制器的比例项增益Kp、微分项增益Kd以及微分阶次μ；②扩张状态观测器的κ、λ、β1、β2、β3、δ、u1，u2。数目n＝11，设待优化参数个体为xi（i＝0，1，…，n－1），中间代个体为x－i（i＝0，1，2，…，n－1），参数的适应度函数记为fi（i＝0，1，…，n－1），历史最优个体及其适应度函数记为Ib和Fb，变异概率记为Pm，最大迭代代数记为G1。采用遗传算法优化控制器参数的步骤如下：

步骤1 确定染色体编码方法。染色体（个体）为

结合11组待优化参数的可能取值范围，采用二进制对参数进行编码，将χ编码为相应位数的二进制串（ρk－1ρk－2… ρ0）满足

式中，k为χ对应的二进制编码的位数；

步骤2 如果达到最大迭代代数，则算法终止，反之则执行步骤3；

步骤3 通过式（12）选择出中间代的n个个体。

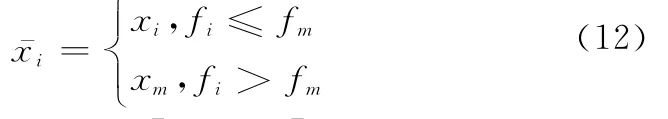
式中，i＝0，1，…，n－1；m为［0，n－1］之间的随机整数，且满足m≠i；

步骤4 对产生的中间个体进行交叉运算，本文中选取交叉概率为100%；

步骤5 对所有个体进行变异操作，变异概率为Pm；

步骤6 计算个体的适应度值，控制器设计的目标为减小回路误差，抑制系统超调量。因此选取优化目标函数为

式中，e（t）为俯仰角信号与俯仰角指令信号的偏差；h为俯仰角信号的最大值与稳态值的差；ε1和ε2分别为误差和超调量的加权系数；

步骤7 选出当代最优个体并与历史最优个体比较，若优于历史最优个体，则用当代最优个体替换历史最优个体，对历史最优个体进行更新，否则，将当前代的一个个体用历史最优个体替换后继续寻优；

步骤8 判断得到的最优解是否满足停止准则，若满足，则输出最优解，否则跳到步骤2继续进行寻优。

当迭代代数达到G1后，将采用遗传算法优化后控制器参数的最优解取出，作为上层粒子群算法的初始种群，对遗传算法得到的最优解进一步进行优化，运行一定代数G2之后，若满足停止准则，则将粒子群优化的结果作为最优结果输出，若不满足停止准则，则用粒子群种群中的q个粒子随机替换掉遗传算法子群中的q个粒子，对遗传算法子群再一次进行优化求解，不断循环，直到控制器参数满足停止准则，输出最优解。采用粒子群算法对控制器参数进行优化时，惯性权值和参数收敛速度密切相关，较大的惯性权值有利于全局搜索，较小的惯性权值有利于算法的局部开发，加速算法的收敛。本文通过设计动态惯性权值来提高粒子收敛速度，更新粒子的位置和速度的表达式为

式中，r1和r2为［－1，1］内相互独立且服从均匀分布的随机数；g1和g2为给定常数，分别为其靠近自身局部最优解的权重和靠近全局最优解的权重；vi（j）为粒子i在第j代的速度；li（j）为粒子i在第j代的位置；Pi（j）为粒子i在第j代的最优位置；Pg（j）为第j代全局最优位置。设动态惯性权值的表达式为

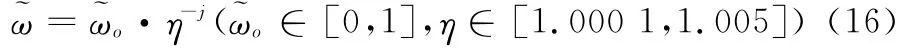
从式（16）可以看出，随着迭代次数的增多，惯性权值减小，而较小的惯性权值可以加快算法的收敛速度。

上层粒子群算法的流程如下：

步骤1 对种群进行初始化，选取底层遗传算法的最优解作为粒子群算法种群的位置，并随机产生每个粒子的速度；

步骤2 判断是否到达最大迭代数，若到达，则算法终止，反之则执行步骤3；

步骤3 计算粒子群算法种群每个粒子的适应度函数值；

步骤4 更新粒子群算法种群的个体极值和全局极值；

步骤5 按照式（14）和式（15）更新粒子群算法中每个粒子的速度和位置；

步骤6 判断优化得到的最优解是否满足停止准则，若满足，则输出最优解，反之，跳转到步骤2继续进行参数优化。

5 仿真验证

本文以某型号火箭发射过程中相关秒点的系统参数为例，考虑一阶弹性振动，对系统进行仿真，标称模型的参数取值为

采用改进的Oustaloup滤波方法对分数阶控制器进行近似，拟合频率ωb＝0.000 1，ωh＝1 000；阶次N＝5。采用基于遗传算法和粒子群优化的分层算法对分数阶PDμ和扩张状态观测器的参数进行整定。设采用遗传算法迭代500代；采用粒子群算法迭代100代；优化得到的分数阶控制器参数为Kp＝1.52，Kd＝2.83，μ＝0.89；扩张状态观测器的参数κ＝0.86；λ＝0.15；β1＝9.21；β2＝90.32；β3＝0.91；δ＝0.06；u1＝0.26，u2＝0.17。

与运载火箭控制器的传统离线设计方法类似，本文提出的方法也主要用于离线设计，避免了由于优化算法耗时带来工程应用上的不便。由于火箭姿态控制系统主要考虑的是姿态角偏差的消除，并使箭体按照选定的轨道和给定的程序角飞行，分别在不存在干扰和不确定性的标称情况和存在内外干扰的不确定情况下，给定系统一个初始俯仰角偏差，对系统进行仿真，并将本文所提控制算法与传统动态增益+静态增益的控制方式以及单纯的分数阶控制器进行对比：

情况1 标称情况下，俯仰角存在5°的初始偏差；

情况2 存在风干扰，俯仰通道干扰力，参数向下摄动30%，其中＝0.005 8s－1，αw＝57.25°＝0.007 9 s－2，俯仰角存在5°初始偏差。

在标称情况下得到的仿真结果如图2～图4所示，其中，PD表示采用传统的动态增益+静态增益的控制方式；FOC表示采用普通的分数阶控制器；DRFOC表示采用本文提出的自抗扰分数阶控制器。可以看出，ESO可以很好地跟踪俯仰角信号，自抗扰分数阶控制具有较快的调节时间、较小的超调量和较小的稳态误差；在稳态条件下角速率信号的振幅也明显小于传统的PD控制和单纯的分数阶控制，具有更好的动态性能和控制精度，可以满足运载火箭对控制系统精度和动态性能的要求。

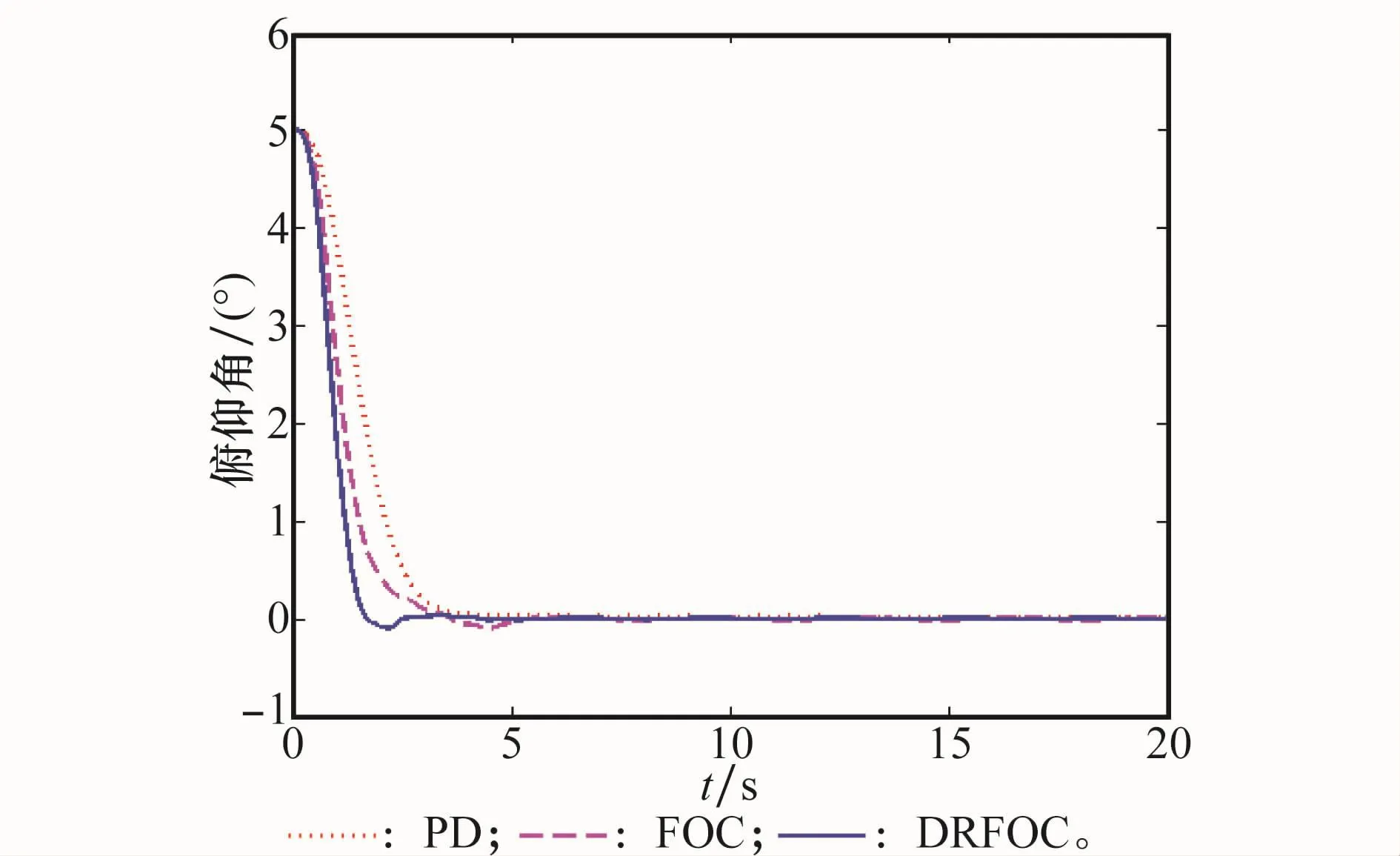
图2 标称情况下俯仰角响应曲线

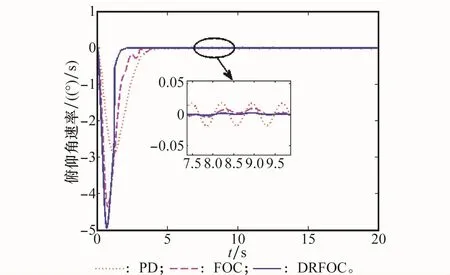
图3 标称情况下俯仰角速率响应曲线

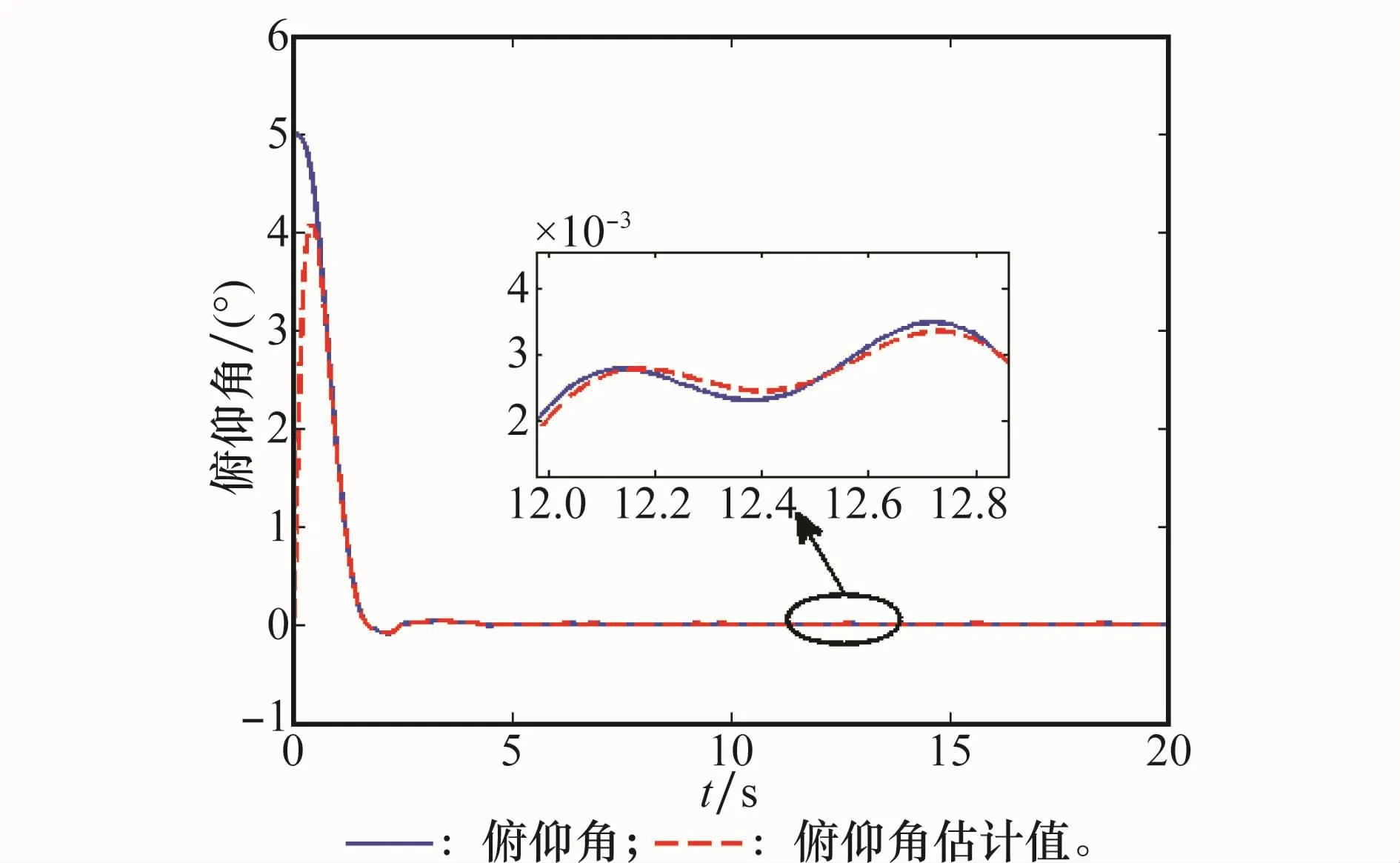
图4 标称情况下ESO跟踪曲线

在不确定情况下得到的仿真结果如图5～图7所示，可以看出，在不确定情况下，系统性能均有所下降，但是由局部放大图可知，自抗扰分数阶控制系统受到扰动的影响更小，性能下降较小，可以保证系统良好的动态性能和控制精度，采用的ESO可以很好地跟踪俯仰角信号，而采用传统的PD控制和分数阶控制器，在受到外界干扰时，角度存在稳态误差，角速率信号在稳态也存在振荡现象，表明了自抗扰分数阶控制器具有较强的鲁棒性和抗扰性。

图5 不确定情况下俯仰角响应曲线

图6 不确定情况下俯仰角速率响应曲线

图7 不确定情况下ESO跟踪曲线

6 结 论

本文针对运载火箭的姿态控制问题，设计了分数阶自抗扰控制器。设计ESO对系统中存在的内外不确定项进行估计。采用分数阶控制器对火箭姿态进行控制并实时补偿ESO估计的干扰，考虑到分数阶控制器和ESO参数多且难以被确定的问题，将粒子群算法和遗传算法结合起来，设计分层优化算法对参数进行优化。仿真验证了所设计的控制方法具有较好的控制精度和较强的鲁棒性。

［1］Li J W.Modeling，design and analysis of large strap-on launch vehicle's attitude control system［D］.Changsha：National University of Defense Technology，2011.（李家文.大型捆绑火箭姿态控制系统的建模、设计与分析［D］.长沙：国防科学技术大学，2011.）

［2］Roshanian J，Saleh A R，Jahed-Motlagh M R.On the design of adaptive autopilots for a launch vehicle［J］.Proc.of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2007，221（1）：27-38.

［3］Oh C S，Bang H，Park C S.Attitude control of a flexible launch vehicle using an adaptive notch filter：ground experiment［J］.Control Engineering Practice，2008，16（1）：30-42.

［4］Wang Q，Wang Z，Dong C Y.Attitude control of flexible launch vehicles based on second-order sliding mode［J］.Journal of System Simulation，2009，21（7）：2006-2009.（王青，王昭，董朝阳.一种基于二阶滑模的柔性运载火箭姿态控制［J］.系统仿真学报，2009，21（7）：2006-2009.）

［5］Zamani M，Karimi-Ghartemani M，Sadati N，et al.Design of a fractional order PID controller for an AVR using particle swarm optimization［J］.Control Engineering Practice，2009，17（12）：1380-1387.

［6］Huang L L，Zhou X L.The adaptive design of the fractional order PID controller parameters［J］.Systems Engineering and Electronics，2013，35（5）：1064-1069.（黄丽莲，周晓亮.分数阶PID控制器参数的自适应设计［J］.系统工程与电子技术，2013，35（5）：1064-1069.）

［7］Zhang B T，Pi Y G.Integration of fuzzy and sliding mode control based on fractional calculus theory for permanent magnet synchronous motor［J］.Przeglad Elektrotchniczny，2011，87（11）：251-255.

［8］Li G Y，Guo C，Li Y X.Fractional-order control of USV course based on improved PSO algorithm［J］.Systems Engineering and Electronics，2014，36（6）：1146-1151.（李光宇，郭晨，李延新.基于改进粒子群算法的USV航向分数阶控制［J］.系统工程与电子技术，2014，36（6）：1146-1151.）

［9］Huang L L，Zhou X L，Xiang J H.Self-adjusting design on parameters of the fractional order PID controller［J］.Systems Engineering and Electronics，2013，35（5）：1064-1069.（黄丽莲，周晓亮，项建弘.分数阶PID控制器参数的自适应设计［J］.系统工程与电子技术，2013，35（5）：1064-1069.）

［10］Han J Q.From PID to active disturbance rejection control［J］.IEEE Trans.on Industrial Electronics，2009，56（3）：900-906.

［11］Li S L，Yang X，Yang D.Active disturbance rejection control for high pointing accuracy and rotation speed［J］.Automatica，2009，45（8）：1854-1860.

［12］Xia Y Q，Dai L，Fu M Y，et al.Application of active disturbance rejection control in tank gun control system［J］.Journal of the Franklin Institute，2014，351（4）：2299-2314.

［13］Guo B Z，Zhao Z.On the convergence of an extended state observer for nonlinear systems with uncertainty［J］.Systems& Control Letters，2011，60（6）：420-430.

［14］Guo B Z，Zhao Z L.On convergence of non-linear extended state observer for multi-input multi-output systems with uncertainty［J］.IET Control Theory&Applications，2012，6（15）：2375-2386.

［15］Xia Y Q，Zhu Z，Fu M Y，et al.Attitude tracking of rigid spacecraft with bounded disturbances［J］.IEEE Trans.on Industrial Electronics，2011，58（2）：647-659.

［16］Fang Y C，Shen H，Sun X Y，et al.Active disturbance rejection control for heading of unmanned helicopter［J］.Control Theory&Applications，2013，30（11）：238-243.（方勇纯，申辉，孙秀云，等.无人机航向自抗扰控制［J］.控制理论与应用，2013，30（11）：238-243.）

［17］Kang Y，Li D H，Lao D Z.Performance comparison of active disturbance rejection control and sliding mode control in spacecraft attitude control［J］.Control Theory&Applications，2013，30（12）：1623-1629.（康莹，李东海，老大中.航天器姿态的自抗扰控制与滑模控制的性能比较［J］.控制理论与应用，2013，30（12）：1623-1629.）

［18］Zhu Z，Xu D，Liu J M，et al.Missile guidance law based on extended state observer［J］.IEEE Trans.on Industrial Electronics，2013，60（12）：5882-5891.

［19］Ma Y Y，Tang S J，Guo J，et al.High angle of attack control system design based on ADRC and fuzzy logic［J］.Systems Engineering and Electronics，2013，35（8）：1711-1716.（马悦悦，唐胜景，郭杰，等.基于自抗扰与模糊逻辑的大攻角控制系统设计［J］.系统工程与电子技术，2013，35（8）：1711-1716.）

［20］Jiao B，Lian Z，Gu X.A dynamic inertia weight particle swarm optimization algorithm［J］.Chaos，Solitons&Fractals，2008，37（3）：698-705.

［21］Jin M，Lu H X.A multi-subgroup hierarchical hybrid of genetic algorithm and particle swarm optimization［J］.Control Theory&Applications，2013，30（10）：1231-1238.（金敏，鲁华祥.一种遗传算法与粒子群优化的多子群分层混合算法［J］.控制理论与应用，2013，30（10）：1231-1238.）

［22］Zhang Y，Su G S，Yan L B.Cooperative optimization algorithm based on particle swarm optimization and Gaussian process［J］.Systems Engineering and Electronics，2013，35（6）：1342-1347.（张研，苏国韶，燕柳斌.基于粒子群优化与高斯过程的协同优化算法［J］.系统工程与电子技术，2013，35（6）：1342-1347.）

［23］Ran M P，Wang Q.Spacecraft rendezvous trajectory optimization method based on EPSO［J］.Journal of Astronaustic，2013，34（9）：1195-1201.（冉茂鹏，王青.一种基于EPSO的航天器交会轨迹优化方法［J］.宇航学报，2013，34（9）：1195-1201.）

Disturbance rejection fractional-order controller design for launch vehicle

CHENG Hao-yu1，DONG Chao-yang1，WANG Qing2
（1.School of Aeronautic Science and Technology，Beihang University，Beijing 100191，China；2.School of Automation Science and Electrical Engineering，Beihang University，Beijing 100191，China）

A novel controller based on active disturbance rejection control and fractional-order control is proposed for the attitude control of launch vehicle.An extended state observer is designed to estimate the impact from parametric uncertainties and disturbances by taking full advantage of the information from the gyros and the attitude sensors.A fractional-order controller is proposed to realize the attitude control by compensating the disturbances.A variable parameter is brought to expand the tuning range and obtain higher control accuracy.A hybrid algorithm based on genetic algorithm and particle swarm optimization is proposed to tune the parameters of the controller.Simulation results show that the controller exhibits better dynamic performance，higher ability in disturbance rejection and stronger robustness against the disturbances.

attitude control；extended state observer（ESO）；fractional-order controller；genetic algorithm；particle swarm optimization

V 448.1 文献标志码：A DOI：10.3969／j.issn.1001-506X.2015.09.23

程昊宇（1990-），男，博士研究生，主要研究方为飞行器制导与控制、飞行器总体设计、鲁棒控制。

E-mail：chenghaoyu＠buaa.edu.cn

董朝阳（1966-），男，教授，博士研究生导师，主要研究方向为飞行器建模、飞行器制导与控制、鲁棒控制。

E-mail：dongchaoyang＠buaa.edu.cn

王 青（1968-），女，教授，博士研究生导师，主要研究方向为导航制导与控制、鲁棒控制、自抗扰控制。

E-mail：wangqing＠buaa.edu.cn

2014-08-27；

2015-03-01；网络优先出版日期：2015-04-28。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150428.1651.003.html

国家自然科学基金（61273083）资助课题