ANSYS仿真在轴系摩擦振动中的应用

2015-07-26侍红岩单晓敏吴晓强张春友

轴承 2015年9期

侍红岩，单晓敏，吴晓强，张春友

(内蒙古民族大学机械工程学院，内蒙古通辽 028000)

船舶轴系的摩擦振动不但会产生噪声污染，而且会引起轴系零件的损耗，从而严重威胁机械结构的安全性，大大缩减零件的寿命。近年来，水润滑橡胶合金轴承在船舶轴承系统中的应用广泛，然而，水润滑橡胶合金轴承在低速、重载等工况下，会由于润滑不良大大降低工作性能。为了解决这一问题，需要对轴承摩擦振动特性进行全面分析。

目前国内外学者对于摩擦振动主要集中在刹车制动系统上[1-2]。文献[3-5]提出了需对摩擦振动全面深入研究以及摩擦振动的重要性。文献[6]提出法向力波动和其引起的摩擦之间的时间延迟是一个激励源，为摩擦系统启动或维持啸叫的振动提供能量。此外，在试验中发现，摩擦振动可能只发生在一部分行程中，也可能存在于整个行程中，主要决定因素是法向作用力、相对速度等试验初始条件。文献[7]采用ADAMS和ANSYS研究了在变载荷作用下，考虑轴系倾斜角的轴系摩擦学、动力学、刚度和强度分析问题。文献[8]研究了水润滑径向橡胶轴承产生自激摩擦振动的原理，发现轴承在低转速下，尤其是在机械启停时, 轴承处于干摩擦状态，由于润滑不良，易产生自激摩擦振动，当转速增大时，振动与噪声现象得到很好的控制。下文针对目前水润滑轴承系统在低速、重载工况下存在的性能问题，利用ANSYS软件建立水润滑橡胶合金轴承的有限元分析模型，探讨轴系摩擦振动特性的具体影响因素，并对水润滑橡胶轴系进行静力分析。

1 轴系摩擦振动的产生机理

任何机械运动系统都不可避免地产生摩擦，而接触面的不良摩擦特性往往是造成机械振动和噪声的根源。摩擦振动是各种内、外因相互激励作用的结果，其产生机理有：粘着-滑动机理、摩擦力与速度负斜率机理、模态耦合机理、自锁-滑移机理、热点理论等[9-10]。其中，摩擦力与速度负斜率机理和模态耦合机理对于轴系摩擦振动的产生解释更为合理。

2 轴系摩擦振动的有限元分析步骤

有限元法是现代工程数值分析中应用广泛的一种方法。用ANSYS解决振动问题一般包括模态分析和静力学分析。

模态分析的一般步骤：

1)建立三维模型，定义单元类型和材料性质等；

2)定义分析类型，添加约束，进行分析；

3)后处理，扩展模态，把结果写入文件。

静力学分析步骤与其主要区别在于：二者所定义的分析类型不同，因为要得到的参数不同；静力学分析不需要进行扩展模态，因为不存在读取振型的过程。

3 轴系摩擦振动仿真

3.1 轴承的约束模态分析

建立轴承的几何模型如图1所示，基本参数见表1，材料属性见表2。划分单元网格，结合轴承的几何模型，在保证计算精度的条件下，确定其单元类型为八节点 Solid 185六面体单元，即Solid 8node185；添加约束，对铜套外表面进行全约束，对x,y,z方向的平动自由度进行约束。

表1 轴承结构参数

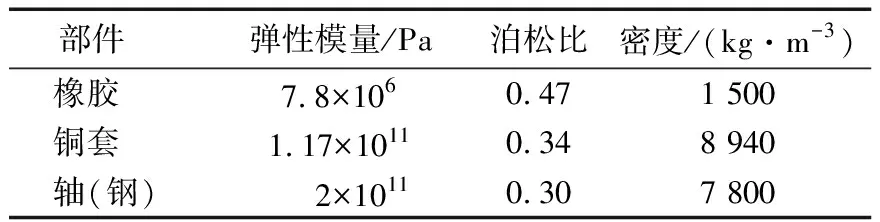
表2 轴承系统各组成部件的材料属性

图1 轴承的有限元模型

在ANSYS软件中分别画出铜轴套和带有水槽的橡胶内衬，但此时二者只是在几何意义上处于接触状态，而实际轴承结构中轴套和内衬是粘结固定在一起的，所以需要对轴套和内衬进行布尔粘结操作，即boolean-glue-volumes。

轴承各阶模态固有频率值见表3。由表可知，轴承的最低固有频率为89.699 Hz，因此只要轴承的振动频率不超过该值就不会发生共振现象。同时轴承的固有频率值在第16阶和第17阶之间以及第24阶和第25阶之间都有突变现象。该现象与轴承结构有关，为了更符合实际构造，套筒和轴套分别采用橡胶和铜。

表3 轴承各阶模态固有频率值

1阶、2阶、16阶、17阶、24阶、25阶轴承模态的振型图如图2所示。

图2 各阶模态振型图

从图中可以看出，在第1阶模态振型中，相对变形量为35.966 μm，变形量不大且分布比较均匀，变形主要集中在轴承两端面处。第2阶模态振型中，相对变形量为34.047 μm，变形主要发生在轴承两端。在第16阶模态振型中，变形量增大且分布不均，表现为间断状态，轴承两端变形集中而中间部分只出现微小的形变。变形量的增加是由于从1阶到16阶模态，其固有频率增加。在第17阶模态下，固有频率产生突变，因此变形分布发生明显变化，从间断分布变为3段分布，即在轴承的中部和其两端面处都有较大的变形量，并且轴承中部的变形量最大。在第24阶模态振型中，轴承的变形不再只分布于某一接触面上，而是扩散在不同的接触面上，变形量仍是3段分布。第25阶模态振型中，固有频率再次突变，变形量增大且变形分布不均匀，变形量逐渐变为4段式分布。由此可知，固有频率的增加会引起变形量增加，这是由于固有频率逐渐接近共振频率；其突变会引起变形量分布变化是由非线性振动系统的跳跃现象特性所致。