基于小波最故优障重构检尺测度方的A法UV推进器

刘维新，　张铭钧，　殷宝吉，　刘　星

基于小波最故优障重构检尺测度方的A法UV推进器

刘维新，张铭钧，殷宝吉，刘星

(哈尔滨工程大学机电工程学院，哈尔滨150001)

针对采用传统小波方法检测外部干扰下自主式水下机器人(AUV)推进器故障时存在的故障检测灵敏度较低问题，提出一种基于小波最优重构尺度确定的AUV推进器故障检测方法，基于小波Shannon熵的小波最优重构尺度确定方法确定离散多层小波分解后细节系数的最优重构尺度，目的是滤除外部干扰等与故障无关信号，并选择故障信息含量最多的最佳重构尺度进行小波单支重构以识别AUV推进器故障特征.AUV实验样机水池实验结果表明，与传统小波方法相比较，所提方法故障检测灵敏度提高了27.78%.

外部干扰；自主式水下机器人；推进器故障；小波；最优重构尺度

自主式水下机器人(Autonomous Underwater Vehicle，AUV)无人无缆在复杂海洋环境中工作，推进器是AUV负荷最重和最易发生故障的部件，从外部干扰影响下的AUV信号中准确检测推进器工作状态，对于提高AUV系统可靠性和保障AUV自主作业具有重要意义[1].

目前，AUV推进器故障检测方法可分为基于定性分析和基于解析模型或数据驱动的定量分析方法[2].基于定性分析的方法如故障树分析法[3]、定性仿真法[4]等，由于存在推理过程匹配冲突等问题，对AUV推进器故障检测效果不佳；基于解析模型的定量分析方法，由于时变外部干扰的影响导致难以建立精确的解析模型[5]，使得基于该类方法检测AUV推进器故障受到了限制；基于数据驱动的定量分析方法无需系统精确解析模型即可对AUV推进器故障进行检测，在AUV故障诊断领域得到了良好的应用[67].

小波方法是一种典型的基于数据驱动的故障诊断方法，用于检测AUV推进器和传感器故障效果良好[8].但在采用传统小波方法检测外部干扰下AUV推进器故障时发现，由于外部干扰的影响，AUV信号信噪比较低，使得经多层小波分解后得到的多频带小波细节系数中，推进器故障特征对应的小波系数模极大值低于外部干扰信号小波系数模极大值，并且由于小波分解后得到的多个频带中故障信息量并不相同，传统小波方法采用最大分解尺度上的小波系数模极大值进行AUV推进器故障检测，存在故障检测灵敏度较低的问题.

针对上述问题，为提高AUV推进器故障检测的灵敏度，本文提出一种基于小波最优重构尺度确定方法的AUV推进器故障检测方法，通过基于小波Shannon熵的小波最优重构尺度确定方法确定离散多层小波分解后细节系数的最优单支重构尺度，目的是滤除外部干扰等与故障无关信号，选择故障信息含量最多的最佳重构尺度以识别AUV推进器故障特征，通过AUV实验样机推进器模拟故障水池实验，对本文方法与传统小波方法的AUV推进器故障检测效果进行对比验证.

1　AUV信号小波分解与重构方法

外部干扰会导致AUV时域信号的波动，影响故障检测结果，需对AUV信号所含外部干扰进行抑制.传统的线性滤波器、五点三次平滑降噪处理方法等AUV外部干扰抑制方法，均相当于一个带通滤波器，仅能得到某一频段上的故障信息而损失了其他频段的故障信息[9].针对该问题，本文采用多层小波分解方法对AUV控制量、状态量信号中所含外部干扰进行抑制.

1.1AUV信号小波分解方法

由于水池实验采集到的AUV控制量、状态量信号为数字信号，而数字信号的分析需采用离散小波变换，离散小波变换是通过对伸缩因子和平移因子的采样而离散化的.离散小波变换方法具体为：将AUV控制量、状态量信号代入式(1)[9]进行多层小波分解，得到对应的二进制离散小波变换逼近系数和细节系数：

式中：Cj(k)为小波逼近系数；Dj(k)为小波细节系数；s(n)为AUV控制量、状态量时域信号；〈〉为内积运算；φ(n)为小波尺度函数；ψ(n)为小波基函数.

根据AUV推进器发生故障后其控制信号和状态信号会发生突变的特性，以及DB4小波基函数检测突变点效果较好的特点[8]，选择DB4小波基函数进行多层小波分解.

1.2AUV信号小波重构方法

在AUV信号离散小波变换中，根据所得多尺度小波分解系数能够进行小波重构，重新获得重构时域信号，但小波函数必须满足容许性条件[10]：

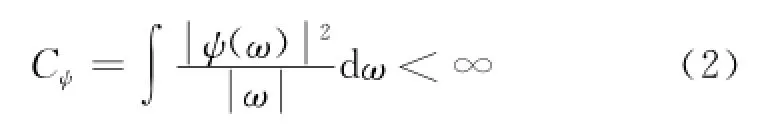
式中，ψ(ω)为小波基函数ψ(n)的傅里叶变换.当满足容许性条件时，小波变换是可逆的，小波重构公式[10]为

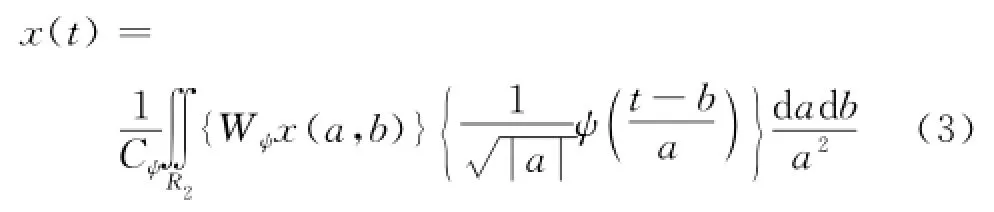
式中：x(t)为小波重构后时域信号；Wψx(a，b)为小波分解所得小波系数；a为小波伸缩因子，b为小波平移因子，实际使用中离散小波变换通常取a=2，b=1.

对小波分解后得到的多尺度小波分解系数进行小波重构，能够得到小波重构后的时域信号.但由于外部干扰的影响，不同分解尺度信号中所含AUV推进器故障信息并不相同，如何选择故障信息相对含量最多的小波分解尺度进行小波重构，对于提高AUV推进器故障检测灵敏度至关重要.

2　小波最优重构尺度确定方法

AUV故障信号经小波分解后得到多个尺度信号，而故障信息在不同尺度的分布量并不相同，如何寻找故障信息含量相对较多而干扰信号含量相对较少的小波尺度信号进行重构以进行故障诊断，是该领域的一个研究热点[1112].本文根据AUV信号离散多层小波分解后不同尺度信号的小波熵值来确定最优重构尺度.

2.1基于小波熵的最优重构尺度确定方法

小波熵的大小与各分解尺度上小波细节系数中所包含的故障信息密切相关，小波熵最小的尺度所包含的故障信息最多[10].为获取AUV信号小波最优重构尺度，首先按照本文1.1节的多层小波分解方法对AUV信号进行分解，然后对各分解尺度的细节系数计算小波熵.即将每一分解尺度的细节系数均视为一个独立信号源W，细节系数数据长度为N，采用下式将细节系数W按处理为概率分布序列[13]，即有

式中：pi为第i个小波系数经处理后对应的概率分布函数值；W(i)为原小波系数序列；N为对应分解尺度的小波细节系数数据长度.

获得小波系数概率分布函数后，计算对应分解尺度小波系数的小波熵：

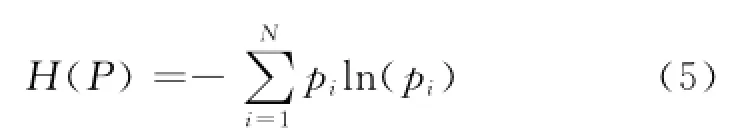
式中：H(P)为小波熵值；pi为第i个小波系数经处理后对应的概率分布函数值；N为对应分解尺度的小波细节系数数据长度.

小波熵值反映了对应分解尺度小波细节系数的稀疏性程度，其值的大小与所包含的故障信息密切相关，故障的发生会影响小波细节系数的概率分布函数，造成概率分布不均匀，进而降低小波熵的值.因此，对于AUV信号经离散多层小波分解后得到的各分解尺度小波系数的小波熵来说，小波熵值最小的尺度包含的故障信息相对最多，更利于推进器故障的检测.根据文献[8]的研究成果，首先对AUV信号进行4层小波分解，然后从这4层小波分解尺度中寻找小波熵最小的尺度.

2.2基于小波最优重构尺度确定的AUV推进器故障检测方法

由于小波分解后得到的多个频带中故障信息量并不相同，传统小波方法采用最大分解尺度上的小波细节系数进行故障检测，存在故障检测灵敏度较低的问题，需确定故障信息相对含量最多的小波分解尺度，以之作为小波最优重构尺度.针对这一问题，采用小波熵来评价小波分解后各分解尺度中故障信息含量，与传统小波方法仅利用最大小波分解尺度上的小波细节系数进行故障检测不同，本文方法基于小波熵方法确定的小波最优重构尺度，故障信息相对含量最多，对该尺度进行小波单支重构，得到AUV推进器故障检测结果，本文所提方法流程如图1所示.

图1　方法流程图Fig.1　Overall structure of the proposed Mäethod

图中，离散多层小波分解方法、小波重构方法在本文第1节有详细实现步骤，小波熵计算方法和最优重构尺度确定方法在本文2.1节进行了详细描述，基于上述方法的结合，以实现本文提高外部干扰下AUV推进器故障检测灵敏度的目的.

3　水池实验验证

为验证所提方法的有效性，通过“海狸II”开架式AUV实验平台进行水池实验，分别采用本文所提方法和传统小波方法，对AUV左主推进器模拟故障进行检测，并对两种方法的检测结果进行对比分析，具体实验载体、故障模拟方法和实验结果如下.

“海狸II”AUV和外部干扰模拟装置分别如图2、3所示.为模拟AUV推进器推力损失故障，采用改变驱动器输出电压的软故障模拟方式[9]，模拟了AUV左主推进器推力损失程度为30%的故障，所得AUV控制量、状态量信号分别如图4所示，从第100节拍起模拟故障，直至实验结束.

图2　海狸IIAUVFig.2　Beaver 2 AUV

图3　外部干扰模拟装置Fig.3　Simulated device of external disturbance

图4　AUV控制量和状态量时域信号Fig.4　Control voltages and state variables of AUV

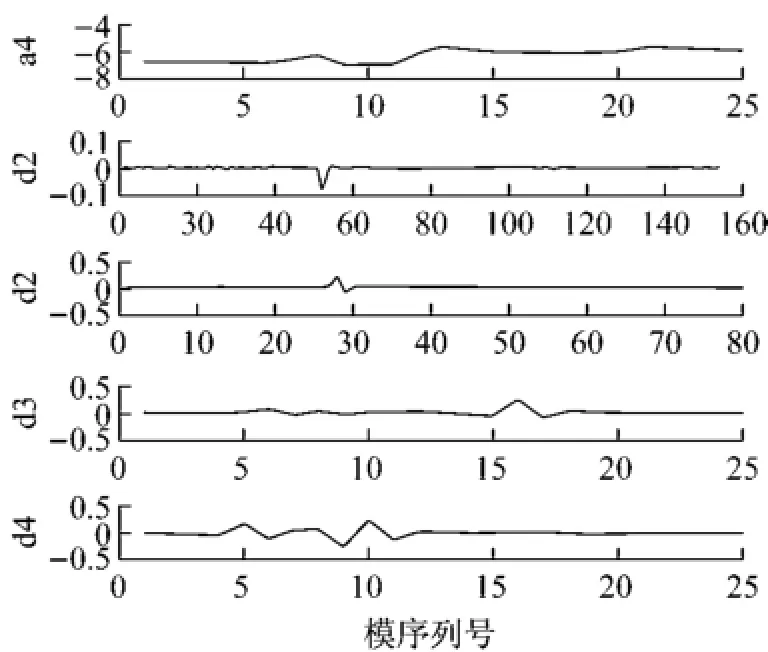
图5　AUV信号小波分解系数Fig.5　Coefficients of AUV wavelet decomposition

表1　各分解尺度小波熵Tab.1　Wavelet entropy for each decomposition scale

采用本文1.1节所述小波分解方法对图4中AUV左主推进器电压进行4层离散小波分解，得到分解后小波系数如图5所示.

根据本文2.1节所述小波熵计算方法，计算图5中各分解尺度小波细节系数小波Shannon熵，计算结果如表1所示.

由表1可知，小波熵最小的尺度为d3尺度.采用d3尺度的小波细节系数进行小波单支重构，得到本文方法对AUV推进器故障检测结果如图6所示.

图6　方法检测结果Fig.6　Detection result based on the proposed Mäethod

由于本文采用的推进器软故障模拟方法故障发生时序列位置可事先设置，而在本次实验中故障真实发生时刻被设置为100节拍处，而由图6可知，本文方法检测出AUV推进器故障发生在时序列位置104节拍处，因此，本文方法检测结果与真实故障发生时刻相差仅4个节拍.而根据传统小波方法基于最大分解尺度上细节系数模极大值方法检测故障的技术路线，由图5可知，模极大值所在位置为第4层小波分解尺度的模序列号9所在位置，根据小波理论，其检测出的AUV推进器时序列位置为9×24= 144节拍处，与真实故障发生时刻100节拍相差44个节拍.本文方法与传统小波方法相比较，故障灵敏度相对提高了(144-104)/144=27.78%，水池实验结果证明了本文所提方法的有效性.

4　结　语

本文基于小波理论和Shannon熵理论研究AUV推进器故障检测问题，提出一种基于小波最优重构尺度确定方法的AUV推进器故障检测方法，通过水池实验对比分析了本文与传统小波方法对AUV推进器故障检测的灵敏度，研究结果表明：对于AUV推进器推力损失30%故障，本文方法比传统小波方法故障检测灵敏度相对提高了27.78%.

[1]朱大奇，胡震.水下机器人故障诊断与容错控制技术[M].北京：国防工业出版社，2012.

[2]周东华，史建涛，何潇.动态系统间歇故障诊断技术综述[J].自动化学报，2014，40(2)：161171.

[3]边信黔，牟春晖，严浙平，等.基于故障树的无人潜器可靠性研究[J].中国造船，2011，52(1)：7179.

[4]王玉甲，张铭钧，储振忠.水下机器人推进器故障定性诊断模型研究[J].南京理工大学学报，2011，35 (S2)：273276.

[5]Zhang Mingjun，Chu Zhenzhong.Adaptive sliding mode control based on local recurrent neural networks for underwater robot[J].Ocean Engineering，2012，45：5662.

[6]周媛，朱大奇.水下机器人传感器故障诊断的灰色预测模型[J].中国造船，2011，52(1)：137144.

[7]Chu Zhenzhong，Zhang Mingjun.Fault reconstruction of thruster for autonomous underwater vehicle based on terminal sliding mode observer[J].Ocean Engineering，2014，88：426434.

[8]王丽荣，徐玉如.水下机器人传感器故障诊断[J].机器人，2006，28(1)：2529.

[9]吴娟.自主式水下机器人多故障诊断方法研究[D].哈尔滨：哈尔滨工程大学，2011：97102.

[10]李宏坤，刘洪轶，徐福健，等.连续小波最优重构尺度确定方法与故障早期识别[J].机械工程学报，2014，50(17)：6976.

[11]冯辅周，司爱威，饶国强，等.基于小波相关排列熵的轴承早期故障诊断技术[J].机械工程学报，2012，48 (13)：7379.

[12]Barszcz T，Jablonsky A.A novel Mäethod for the optimal band selection for vibration signal demodulation and comparison with the kurtogram[J]. Mäechanical Systems and Signal Processing，2011，25 (1)：431451.

[13]蒋永华，汤宝平，刘文艺，等.基于参数优化Morlet小波变换的故障特征提取方法[J].机械工程学报，2010，31(1)：5660.

(编辑吕丹)

Thruster Fault Detection for Autonomous Underwater Vehicle Based on the Optimal Wavelet Reconstruction Scale Determination

LIU Weixin，ZHANG Mingjun，YIN Baoji，LIU Xing
(College of Mäechanical and Electrical Engineering，Harbin Engineering University，Harbin 150001，China)

Aiming at the unsatisfactory fault detection sensitivity based on the conventional wavelet decomposition for autonomous underwater vehicle(AUV)subject to the external disturbance，a thruster fault detection Mäethod was proposed based on optimal wavelet reconstruction scale determination.In order to filter the irrelevant information，e.g.external disturbance，the optimal reconstruction scale was determined based on Shannon entropy theory for the detailed coefficients obtained from discrete wavelet decomposition.Therefore，fault feature extraction could be achieved by the determined optimal reconstruction scale.In the proposed Mäethod，the fault detection was to be achieved by selecting the modulus maximum of the detailed coefficients obtained from multiresolution wavelet decomposition.PoolexperiMents were perforMäed on the Beaver 2 AUV.The experiMent results showed the sensitivity of fault detection was improved 27.78%in comparison with the conventional wavelet decomposition.

external disturbance；autonomous underwater vehicle(AUV)；thruster fault；wavelet；optimal reconstruction scale

TP 27

A

16717333(2015)02013005

10.3969/j.issn.16717333.2015.02.006

2015-01-14

工业和信息化部基础科研资助项目(B2420133003)

刘维新(1985-)，男，博士生，主要研究方向为自主式水下机器人状态监测与故障诊断技术.E-mail：liuweixin@hrbeu.edu.cn