卫星Stewart隔振平台高可靠性设计及容错控制

许域菲，　赵艳彬，　陈　荷，　袁金如，　高志峰

卫星Stewart隔振平台高可靠性设计及容错控制

许域菲1，赵艳彬1，陈荷1，袁金如1，高志峰2

(1.上海卫星工程研究所，上海200240；2.南京邮电大学自动化学院，南京210023)

介绍了卫星Stewart隔振平台，此隔振平台由6根作动杆组成，可以隔离卫星本体的挠性振动和外部干扰，为有效载荷提供超静力学环境；分析了该Stewart隔振平台高可靠性构型设计，基于牛顿欧拉法推导了雅克比矩阵，设计了正交解耦构型；分析了作动杆发生故障时的情况，并结合其动力学模型，重构解耦矩阵，实现了容错控制，提高了隔振平台的可靠性.在某卫星上进行了仿真实验，结果表明本文所提的解耦设计和容错控制方法是有效的.

卫星隔振；解耦设计；容错控制；Stewart平台

现代空间光学载荷要求极高的指向精度和姿态稳定度，如新一代空间望远镜JWST要求0.01 μrad的指向精度，激光通信平台需要微弧度级指向精度，空间迈克尔逊空间干涉仪需要10 nm的位置控制精度.我国当前卫星平台远不能满足现代空间光学载荷的超静力学环境和超准指向精度要求.同时航天器的柔性越来越大，低频模态密集，航天器上的扰动源，如斯特林制冷机、反作用飞轮、太阳帆板驱动机构等工作的时候会产生随机扰动和振动，虽然空间微振动幅值小，但是频带宽，对于高性能空间光学载荷性能的影响已经不能忽视[12].

为保证敏感载荷的性能，需要控制航天器微振动，在为光学敏感载荷提供超静力学环境的同时，提高指向精度和稳定度.一种有效的方法是采用隔振平台代替传统上连接运载火箭和卫星的适配器[35]，可以有效地隔离振动，改善动力学环境，提高卫星从发射到在轨过程的可靠性和安全性能.Stewart隔振平台是一种有效的星上隔振平台，结构紧凑，刚度高，能满足6自由度控制要求，且运动精度高、平稳，引起了国内外很多学者的关注.

另外，航天设备对可靠性和安全性有着极其苛刻的要求[68]，往往要求硬件备份.Stewart隔振平台结构紧凑，本身并不提供硬件冗余，且Stewart平台的核心部件是作动器，这种主动控制型部件涉及电、磁作用，发生故障的几率较高.因此，为了提高可靠性和安全性，本文对隔振平台构型进行优化设计，首先从构型上实现正交解耦，最大程度消弱各杆之间的耦合作用，提高可靠性；其次，分析作动杆发生故障的情况，并重新设计解耦矩阵，实现隔振平台的容错控制.

纵观国内外学者对Stewart隔振平台的研究，大都着重于其动力学建模、运动学分析、空间位置、隔振性能分析等[9-12].本文的创新点在于对Stewart隔振平台的安全性和可靠性设计问题进行了初步研究，设计了并联连接式的正交解耦构型，从结构上解除耦合影响；考虑其关键部件作动杆发生故障的情况，研究其故障模式，推导了重构控制策略.最后对作动杆的输出力和卫星的姿态进行了仿真验证.本文的研究更进一步证明了Stewart隔振平台在卫星上应用的有效性和可行性.

1　隔振平台解耦设计

1.1静定结构分析

多自由度隔振需要多个主动杆并联组成的平台进行控制，平台的支腿数和构型取决于需要对载荷控制的自由度数以及航天器的结构约束.目前已有多种结构的平台出现，比如三、四、六及八杆平台.如果要求对载荷进行6自由度隔振，则可以采用6自由度Stewart平台的形式，主动杆之间采用正交的形式布局，可最大程度地减少杆之间的耦合，提高可靠性.每一个主动杆都采用同样的结构，主动杆由音圈作动器、传感器和柔性铰链组成.

多自由度平台如图1所示.主动控制时采用音圈作动器，图中{B}，{U}，{P}分别表示基座、惯性和载荷坐标系，惯性坐标系原点与基座原点重合.

下面基于牛顿欧拉法推导其动力学关系.

Ai点的矢量方程为

Ai点的速度方程为

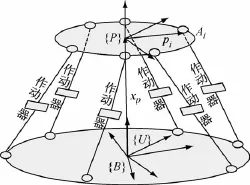
图1　多自由度平台示意图Fig.1　The diagram of a multiDOF platform

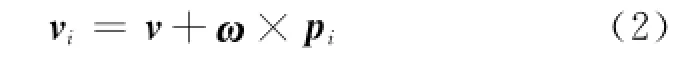
Ai点的速度在主动杆方向投影q为

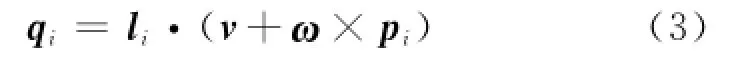
用矩阵表示

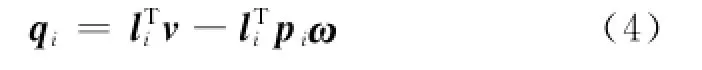
pi是pi的反对称矩阵.

式(4)可进一步转化为

将式(5)写成变分的形式为

式中：δq表示支腿长度变化；δχ表示载荷的广义坐标变量.

由式(6)可知，载荷的运动可以通过支腿的长度变化来完成.多自由度平台构型解耦、优化设计的关键是设计雅克比矩阵J，即支腿数和构型.

矩阵J是联系支腿(主动杆)长度δq和上平台广义坐标δχ的一个重要变量，在对平台进行控制时一般只控制支腿的长度，不控制支腿的转角.平台可以对载荷进行多自由度隔振和定向，支腿数量的多少和平台构型决定了可以控制的载荷自由度.如果固定上平台的6个自由度，代数求解的杆长是唯一的.控制过程中，如果上平台的位置和姿态已知，根据矩阵J可以立即求解支腿长度，但是如果根据支腿长度反解上平台的位置和姿态，却需要6个方程，并且当雅克比矩阵非奇异，才能得到唯一解，即要求6个支腿并且构型满足雅克比矩阵非奇异，才能对上平台载荷进行6自由度控制.

1.2构型优化设计

下面推导最优夹角的设计.Stewart平台相邻2个主动杆相交，如图2所示.不失一般性，假设主动杆1、2的夹角θ，θ∈0，()π，沿主动杆1、2的扰动力分别是f1、f2，如图3所示.为了减少基座振动对载荷的影响，优化θ角.

图2　正交型Stewart平台构型Fig.2　The orthogonal Stewart platform

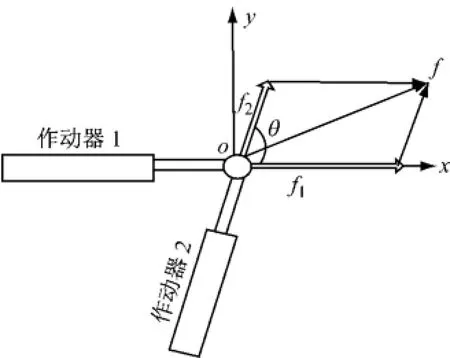
图3　同一个铰链处的两个主动杆Fig.3　Two struts linked in the saMäe joint

根据矢量运算的正交分解，可得f1、f2在x、y坐标轴上的分量为

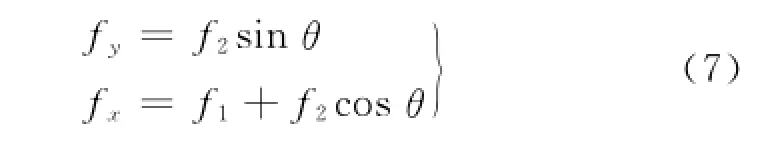
f1和f2的合力f为

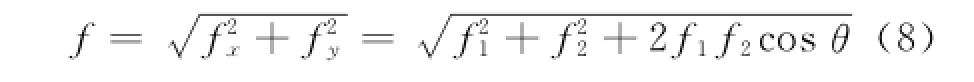
不妨假设f1、f2满足比例关系：

式中，p为正数.合力f表示为

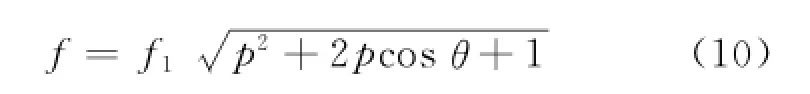
不妨取系数方程

当g′(p)=0时，p值对应的函数g(p)最小，合力f最小，此时所以当p满足p=-cosθ时，合力最小，为fmin= f1sinθ，主动杆振动对载荷的影响也最小.

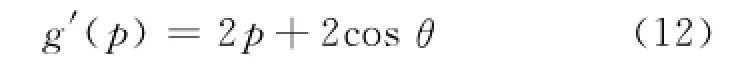
当合力f取最小值时，p∈[-1，1]，并且同时希望合力f的最大值fmax接近最小值fmin.

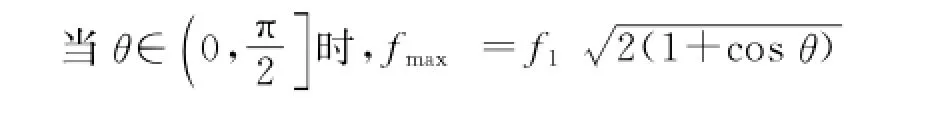
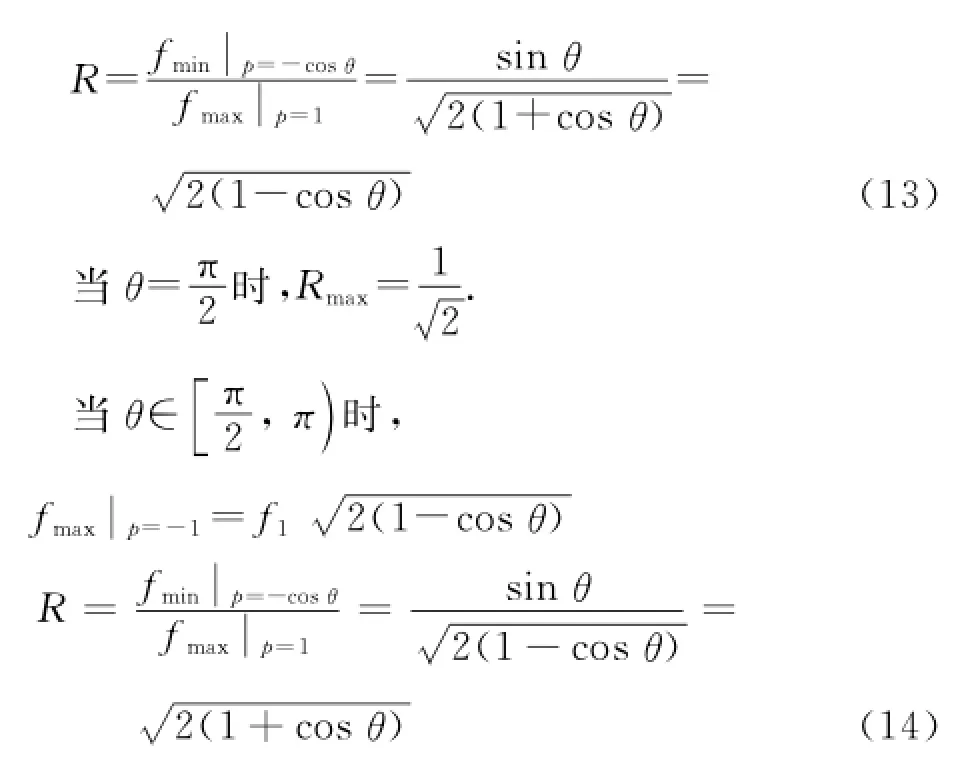
因此，为了使主动杆振动对载荷影响最小，θ=π/2，此时主动杆之间耦合最小，实现了构型的优化和解耦，提高了可靠性，同时便于控制器的设计.

2　故障描述和容错控制

将多自由度隔振平台应用到航空航天任务时，必须考虑可靠性.对于主动隔振平台，作动器失效是容易出现的故障(如波纹管漏气、伺服阀故障等)，对于Stewart式隔振平台，当有1个或2个作动器失效时，剩下的作动器仍能提供6自由度隔振，提高了可靠性.

2.1解耦矩阵描述

定义载荷指向自由度数为r，由指向自由度组成的有效载荷广义坐标χ的分向量记为ρ，有ρ=[ρ1ρ2…ρr]T.令ρn=[ρn1ρn2…ρnr]T，ρni (i=1，2，…r)为χ中对应ρi的元素数，则可定义J的子矩阵为标称解耦矩阵，记为D6×r.结合式(6)，有

式中，D由J中对应指向自由度的列向量组成，即

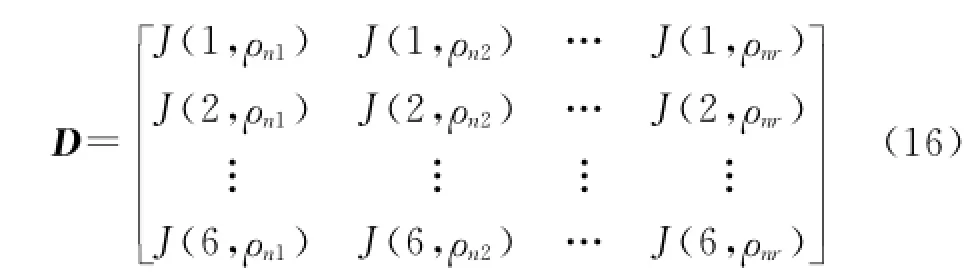
式中，J(i，j)表示J的第(i，j)个要素.

令α=[12…6]，则D可以写为如下更紧凑的形式D=M(α，ρn).在实际应用中，由于作动杆标称位置确定，J是常值矩阵，则D也是常值矩阵.

2.2作动杆重构控制

当6个作动杆中的1个或2个发生故障，本文假设故障类型为卡死故障，即作动器固定在某个位置，不能调节其长度，则上文推导的雅克比矩阵J也随之失效.本节将重构新的解耦矩阵来补偿一个或多个作动杆发生故障带来的影响.

令d是发生故障的第i个作动器排列的向量，有d=[d1d2…ds]T，s∈[1，6]，s是发生故障的作动器的数量，当s个作动器发生了故障，则需要剩余s个自由度上的运动来补偿卡死的作动器，令剩余活动的自由度向量u=[u1u2…us]T.同时，令un=[u1u2…ur]T是对应u的个数向量，则总的载荷位移通过向量u和ρ得到，相应的作动器运动如下表示：

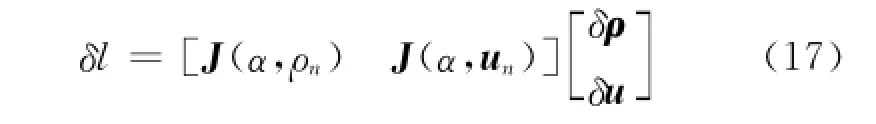
由于发生故障的作动器被卡死，长度不能改变，则有若合理选择则ρ和u构成的增广矩阵为则

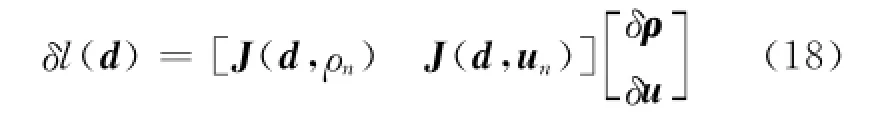
若合理选择

则ρ和u构成的增广矩阵

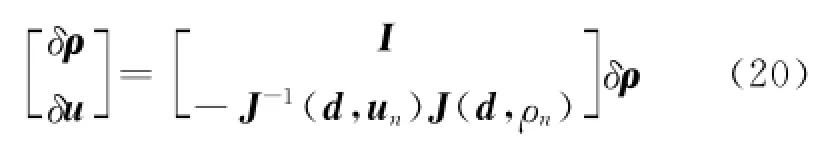
将式(20)代入式(17)，得为重构的解耦矩阵.

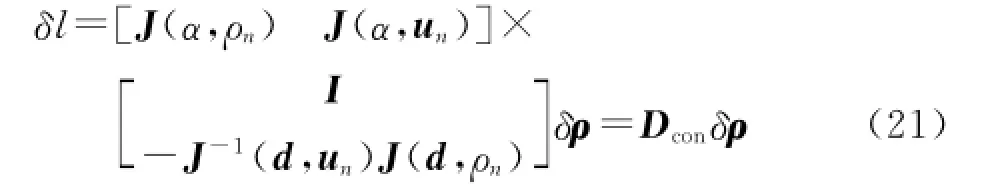
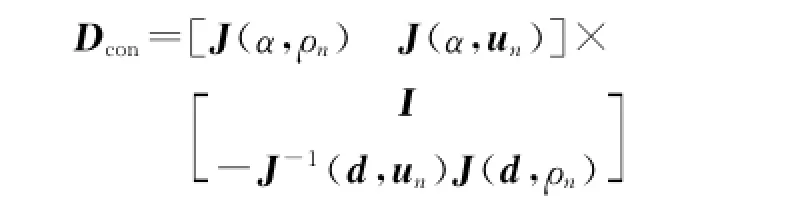
当某几个作动器故障发生时，通过调节剩余完好的作动器的杆长，得到新的解耦矩阵Dcon，并将重构的解耦矩阵Dcon代替原解耦矩阵D，以此来补偿故障的影响.

3　仿真结果

本节基于MATLAB对提出的重构控制算法进行仿真验证.假设卫星本体平台和有效载荷的惯量分别为

假设作动杆5和6同时发生了卡死故障，在数值仿真中，不失一般性，假设卡死后其输出力Fs5=-18 mN，Fs6=20 mN.将上述参数代入卫星姿态控制系统，考察6个作动杆输出力(见图4)，卫星姿态响应仿真结果如图5、6所示.

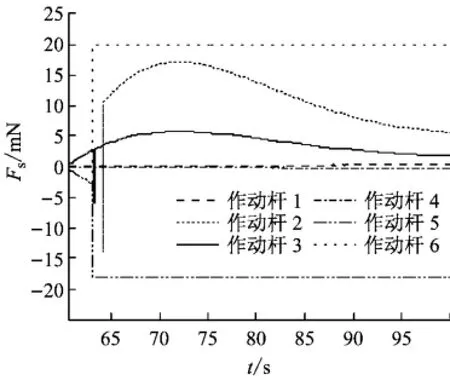
图4　2根作动杆卡死故障后各作动杆输出力Fig.4　The output forces of the struts when two struts are stuck

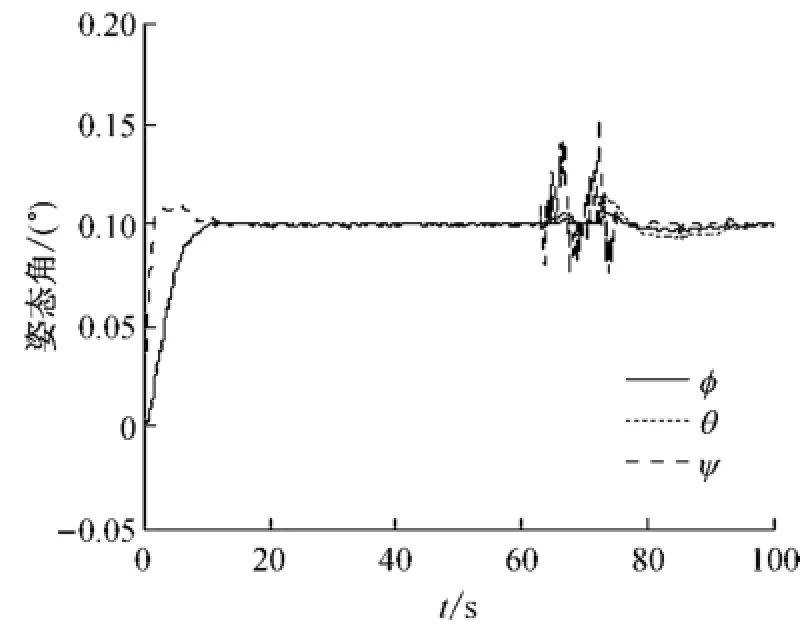
图5　卫星姿态角响应Fig.5　The satellite attitude angle responses

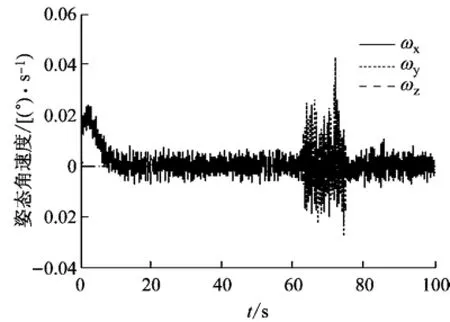
图6　卫星姿态角速度响应Fig.6　The satellite attitude angle velocity responses

由图4可知，63 s时作动杆5和6同时发生了卡死故障，此时其他作动杆进行重构，补偿作动杆5 和6故障的影响.图5和6表明，当发生故障后，卫星的姿态角和姿态角速度发生振荡，但经过重构和补偿后，很快重新进入稳态.

4　结　语

本文针对卫星隔振平台的可靠性应用问题，从构型解耦优化和故障重构控制2个方面进行了研究.首先设计了六杆式Stewart隔振平台作动杆正交解耦构型，分析了其静定结构，从构型上保障隔振平台的可靠性，降低由于作动杆耦合带来的故障牵连效应.其次，分析了一个或多个作动器发生故障的情况，进而设计了容错控制器.本文拓展了Stewart平台的研究范围，对Stewart隔振平台的高可靠性、安全性应用具有重要的参考价值.

[1]金栋平，胡海岩.碰撞振动与控制[M].北京：科学出版社，2005.

[2]刘天雄，林益明，王明宇，等.航天器振动控制技术进展[J].宇航学报，2008，29(1)：112.

[3]涂奉臣，黄文虎，陈照波，等.新型半主动整星隔振平台及其模糊最优控制研究[J].振动工程学报，2010，23(2)：133139.

[4]赵会光，马兴瑞，冯纪生.整星隔振技术若干问题的探讨[J].航天器工程，2011，10(3)：3037.

[5]郑钢铁.空间飞行器隔振与振动抑制研究进展[C]//第九届全国振动理论及应学术会议论文集.兰州：中国振动工程协会，2007：113.

[6]姜斌，冒泽慧，杨浩，等.控制系统的故障诊断与故障调节[M].北京：国防工业出版社，2009.

[7]周东华，叶银忠.现代故障诊断与容错控制[M].北京：清华大学出版社，2000.

[8]McInroy J E.Robustly fault tolerant GoughStewart platforms[C]//IEEE International Conference on Automation Science and Engineering.Madison：IEEE，2013：3844.

[9]刘勺斌，杨洪波，刘洋.基于Stewart平台的空间光学仪器主动隔振系统研究[J].噪声与振动控制，2008，27(2)：1014.

[10]Ukidve C S，McInroy J E.Orthogonal GoughStewart platforms with optimal fault tolerant manipulability[C]//International Conference on Robotics and Automation.Orlando：IEEE，2006：38013806.

[11]Stewart D.A platform with six degrees of freedom [J].Institution of Mäechanical Engineers，1966，180 (15)：371378.

[12]Geng Z J，Haynes L S.Six degreeoffreedom active vibration control using the Stewart platforms[J]. IEEE Transactions on Control System Technology，1994，2(1)：4553.

(编辑俞红卫)

High Reliability Design and Fault Tolerant Control of Satellite Stewart Vibration lsolation Platform

XU Yufei 1，ZHAO Yanbin 1，CHEN He 1，YUAN Jinru 1，GAO Zhifeng2

(1.Shanghai Institute of Satellite Engineering，Shanghai 200240，China；2.School of Automation，Nanjing University of Posts and Telecommunications，Nanjing 210023，China)

The satellite Stewart vibration isolation platform(SVIP)was introduced.The SVIP consisting of six struts could isolate the flexible vibrations and external disturbances from the base body and supply ultraquiet Mäechanical environMent for the payload.The high reliability configuration of SVIP was analyzed，the Jacobian matrix was derived based on NewtonEuler theorem and the orthogonal decoupled configuration was designed.The stuck fault of the strut was taken into account and the decoupled matrix was reconstructed to tolerant the fault，and then the reliability of the SVIP was improved.NuMäerical simulations demonstrated that the proposed approach was efficient.

satellite vibration isolation；decoupled design；fault tolerant control；Stewart p latform

TP 535

A

16717333(2015)02017305

10.3969/j.issn.16717333.2015.02.015

2015-01-15

国家自然科学基金资助项目(11302132，61304106)

许域菲(1984-)，女，工程师，博士，主要研究方向为卫星总体设计和姿态控制.E-mail：xyfnuaa@126.com