基于事件触发的线性网络化控制系统主-被动混合容错控制设计

王　君，　李淑真，　李　炜

(兰州理工大学电气工程与信息工程学院，兰州　730050)

基于事件触发的线性网络化控制系统主-被动混合容错控制设计

王君，李淑真，李炜

(兰州理工大学电气工程与信息工程学院，兰州730050)

针对一类具有时变时延的线性网络化控制系统(NCS)，在离散事件触发通信机制下，研究了执行器任意失效故障的主被动混合容错控制问题.建立了基于事件触发机制的闭环故障系统模型，设计了能使系统在发生故障集以内的故障时稳定的被动容错控制器.同时，设计故障诊断观测器估计任意执行器失效故障的大小，一旦获得准确的故障信息，立即重构控制器以补偿故障的影响.所设计的主被动混合容错控制器在执行器任意失效故障下，不但能使系统稳定而且具有良好的控制性能.仿真算例验证了本文方法可在确保故障系统稳定的前提下能有效地节约网络通信资源.

网络化控制系统；离散事件触发机制；混合容错控制系统；故障诊断观测器

网络化控制系统(Networked Control System，NCS)是通过一个实时网络构成的闭环控制系统，相比于传统点对点数据传输的控制系统，NCS的设计更复杂故障诱发因素更多.因此将容错控制技术引入到NCS的安全性和可靠性的研究中日益受到人们的广泛关注[1-3].

随着复杂度的增加NCS由于有限的网络带宽，使系统面临更加严重的时延、丢包等问题，为了节约有效的网络资源，兼顾网络服务质量(Quality of Service，QoS)和系统控制质量(Quality of Control，QoC)，文献[4]中提出了一种离散事件触发机制，即在每一个采样时刻检测系统的状态并计算相应误差，进而与预先设定阈值比较，判断系统状态数据是否需要传输.NCS中执行器和控制器采用事件驱动显然要比传统的时间驱动方式节约网络资源.

目前NCS容错控制的研究主要有2类，即主动容错控制(AFTC)和被动容错控制(PFTC).时间触发机制下NCS的主、被动容错控制已经做了大量的研究[5-7]，但在事件触发机制下该研究工作还处于起步阶段.文献[8]中针对事件触发机制下的NCS的执行器故障，研究了鲁棒完整性问题.文献[9]中研究了NCS事件触发通信机制和H∞性能控制的协同设计方法.文献[10]中研究了NCS系统在事件触发机制下的可靠控制器的设计.以上研究均为事件触发机制下PFTC，而关于事件触发机制下NCS的AFTC研究未见报道.

虽然PFTC的优点是不需要在线估计故障集以内的故障，设计简单易行，但是当可能出现的故障和系统冗余度增加时，控制器的设计就变得保守且控制性能下降，尤其是当出现故障集之外的故障时，PFTC无容错能力.相比PFTC，AFTC则可以实时检测故障，根据检测的故障大小重新设计控制器从而获得更好的系统性能，但其故障检测需要一定的时间，如果不能及时检测故障并重组控制器则可能导致系统崩溃.

因此综合考虑AFTC和PFTC的优缺点，文献[11]中针对飞行器提出了主-被动混合容错控制，PFTC保持系统稳定性，AFTC优化系统性能，但是文中没有对故障进行估计.文献[12]中针对执行器偏移和卡死故障提出自适应故障补偿和性能优化的主被动混合容错方法.由于上述文献均未涉及具体的故障诊断模块设计且都是针对非NCS，故在研究中既未考虑时延也未考虑网络资源的节约.而针对此类问题的研究目前尚未报道.

本文针对一类具有时变时延的线性NCS，引入离散事件触发通信机制，考虑执行器任意故障情形，研究了主被动混合的容错控制问题.首先将线性NCS的网络属性、故障及触发条件建立在统一的模型中；然后构造适当的Lyapunov泛函、改进的Jensen不等式等方法，采用状态反馈控制策略设计了PFTCS，使得执行器在发生故障集以内的故障或其他故障初期时保持系统稳定或减缓系统恶化速度；同时利用故障诊断观测器对故障进行估计并重构控制器以补偿执行器任意失效故障.最后以仿真算例验证该方法的可行性和有效性.

1　问题描述

1.1离散事件触发机制

NCS事件触发机制下主被动混合容错控制系统结构如图1所示.其中τsc、τca和τc分别表示传感器到控制器、控制器到执行器以及执行器到故障检测观测器的时延.其他计算时延忽略不计.该结构既能节约网络资源又能简化设计过程.其中，事件发生器的作用是在采样时刻依据某种事件发生与否决定系统数据是否需要在网路中传输，同时在设计中将事件发生器放在控制器与执行器之间，以简化故障诊断观测器的设计.

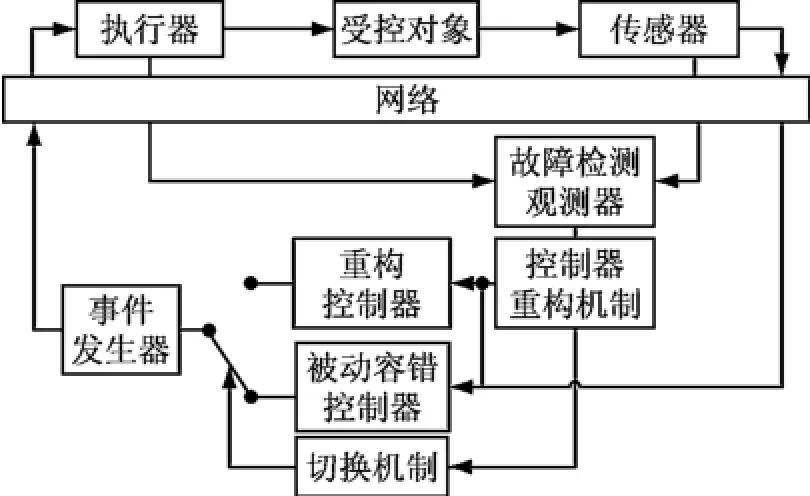
图1　系统结构图Fig.1　A structure diagram of system

为分析方便[8]，首先作如下假设：

(1)传感器和控制器由时钟驱动，设采样周期为h，采样序列描述为；

(2)执行器由事件驱动，定义tkh为信息的传递时刻，传递时刻的集合可以表示为显然，是的子集；

(3)整个过程中，控制和观测的位置相同且不考虑外界干扰和数据丢包[13]；

(4)系统状态完全可测.tkh时刻从传感器到控制器、从控制器到执行器的传输及从执行器到观测器的时延等可合计为，暂不考虑丢包.

为方便FDD设计同时确保系统在性能满足的条件下，仅传输需要的采样数据，创建如下事件触发机制

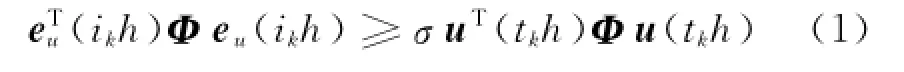
式中

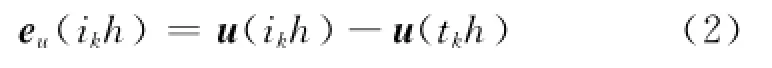
ikh=tkh+l h，l∈Ν，eu(ikh)是当前采样时刻控制器输出u(ikh)与最近传递数据时刻控制器输出u(tkh)的误差.σ>0是一个给定的标量参数，与系统性能有关，Φ是正定的权矩阵.

若满足式(1)，则tk+1h为下一个需要传输数据的时刻.

1.2基于事件触发的闭环故障NCS描述

(1)被控对象.考虑如图1所示的NCS，设被控对象模型为：

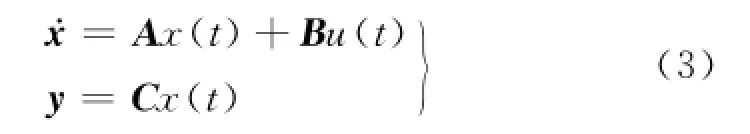
式中：x(t)∈Rn、u(t)∈Rm分别为系统的状态变量、控制输入；y(t)∈RP为测量输出.式(3)的初始条件x(t0)=x0，A∈Rn×n，B∈Rn×m，C∈Rp×n是适当维数的常数矩阵.

(2)事件触发闭环NCS描述.针对式(3)控制对象，采用状态反馈控制器

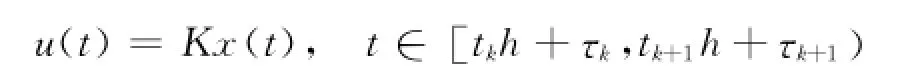
设τ(t)=t-ikh，显然τ(t)是连续的线性函数，且满足0<τm≤τ(t)≤τM，τm、τM分别表示实际网络传输时延的上下界.由式(2)知，(3)事件触发闭环故障系统描述.考虑执行器故障u f(t)=L u(t).其中，L=diag{l1，l2，…，lm}，lq∈[0，1]，q=1，2，…，m.矩阵L表示故障的程度. 当lq=0时，表示第q个执行器完全失效；当lq=1时，表示第q个执行器正常工作；当lq∈(0，1)时，表示第q个执行器部分失效.

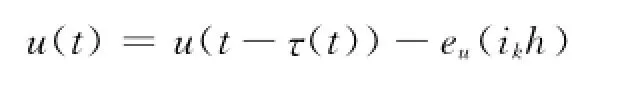
令uf(t)=u(t)-L^u(t)，其中L^=I-L.并设f(t)=L^u(t)为执行器故障的另一种表述.则闭环系统故障模型转化为

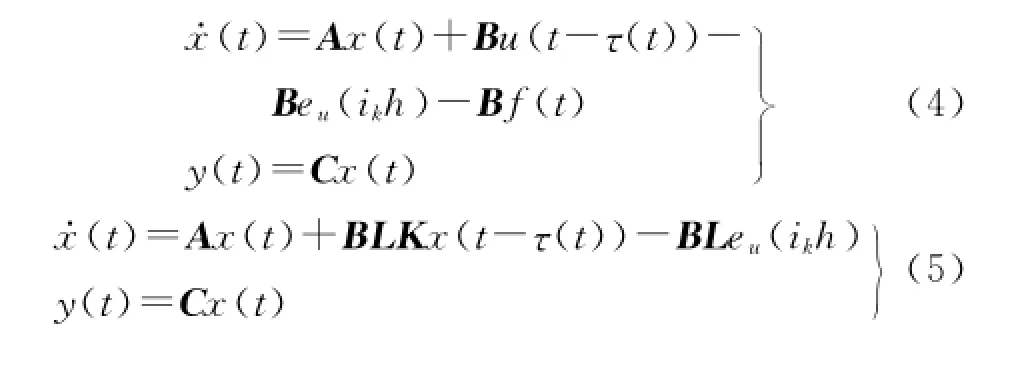
注1式(4)、(5)是等价关系，即形式不同但表示的含义相同，两式都包含了执行器故障，网络传输时延τ(t)，以及事件触发检测变量状态误差eu(ikh)，为后面分别设计被动、主动容错控制器创造了条件.

1.3故障诊断观测器的设计

考虑闭环系统故障模型式(4)，为了估计已经发生的执行器故障，采用结构如文献[13]中的故障诊断观测器：

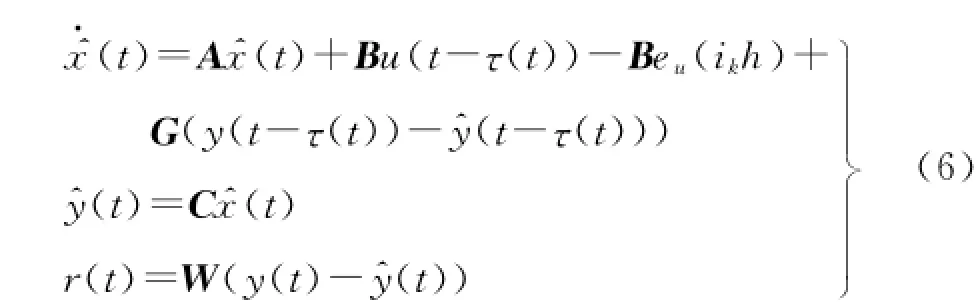
式中：r(t)∈Rn×p为输出残差信号；G、W分别为观测器的增益矩阵和权矩阵.

设估计误差

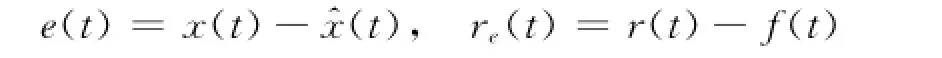
则

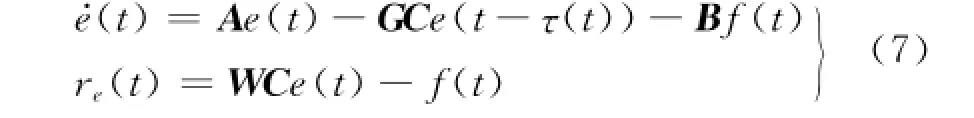
相关引理：

引理1[14]对任意恒定对称矩阵Z∈Rn×n，Z= ZT>0，标量δ>0，矢量函数e·：-δ，[]0→Rn定义以下积分项：

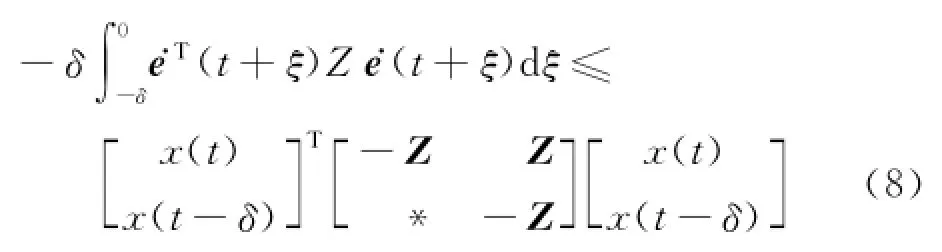
引理2[15]假设f1，f2，…，fN：Rm→R在开集D的子集中有正值，D∈R m，则在集合D中fi的相互凸组合满足

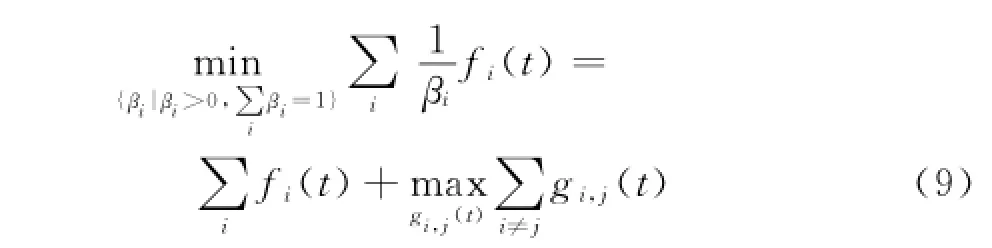
式中，

定理1给定标量正数τm，τM，τs，α，β，γ，如果存在正定对称矩阵P、V、W满足线性矩阵不等式，则故障诊断观测器可使故障估计误差满足.且观测器增益G=P-1V.

式中，*表示由矩阵的对称性得到的矩阵块；而

证明构造Lyapunov-Krasovskii泛函

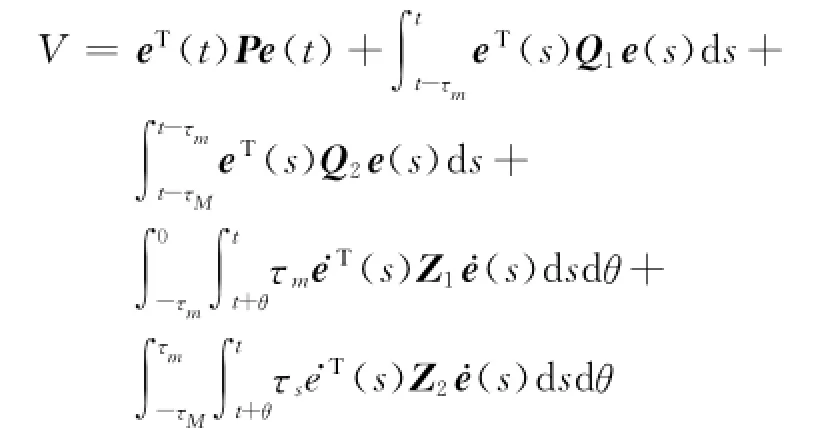
由式(7)，对V两边求导，有

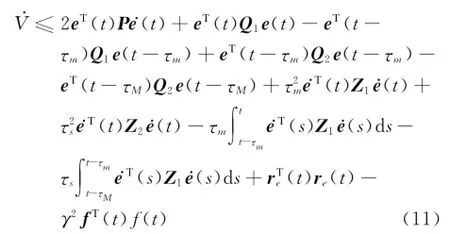
根据引理1、2，得，

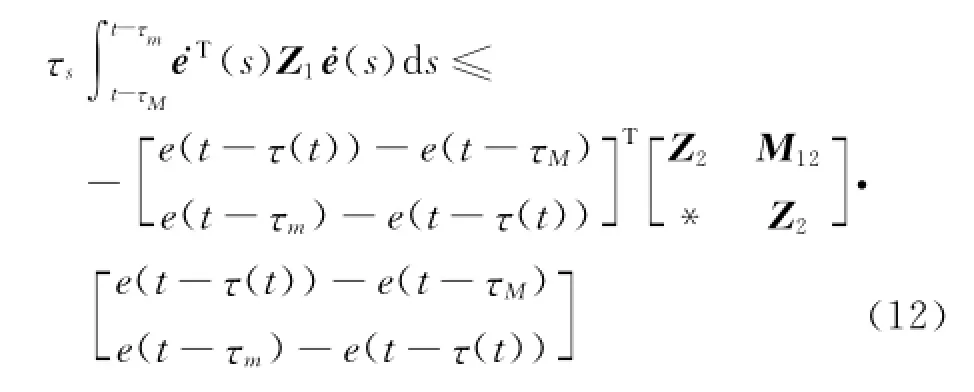
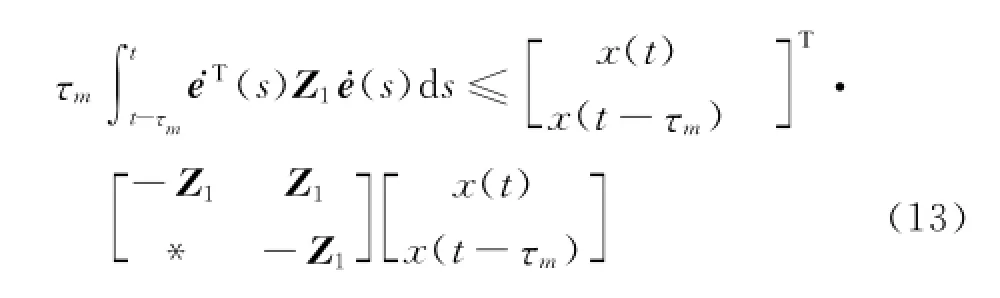
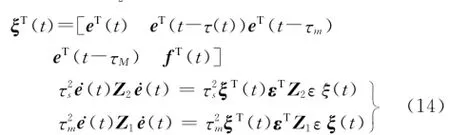
式中，ε=[A-GC 0 0 -B].由式(7)、(11)～(13)得

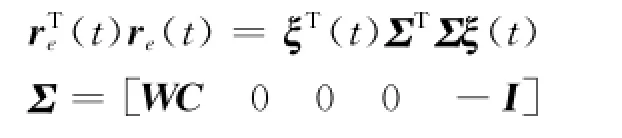
则有

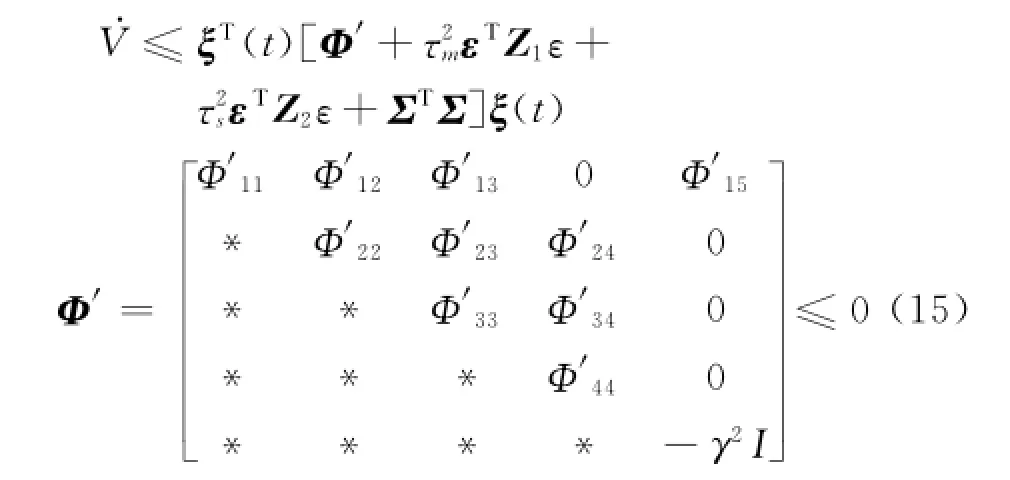
式中：

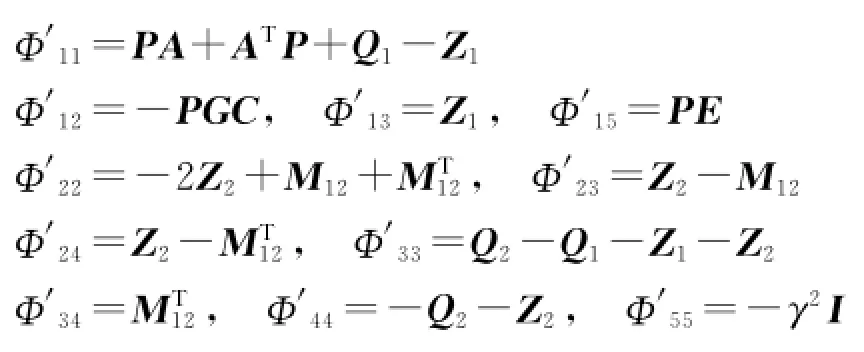
由shur补性质得

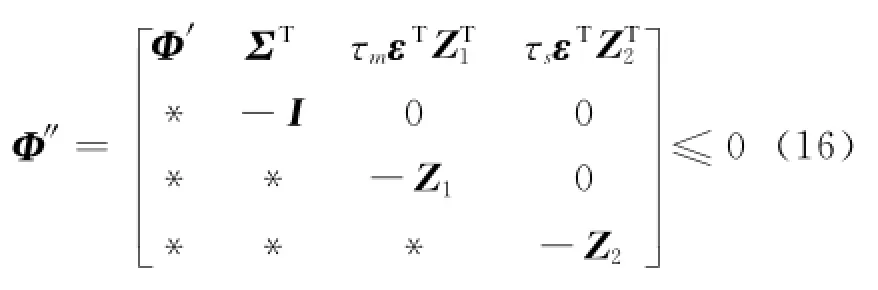
对Φ″应用合同变换，两边同乘

及其转置，令PG=V，由得

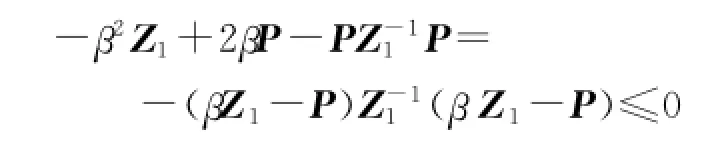
得

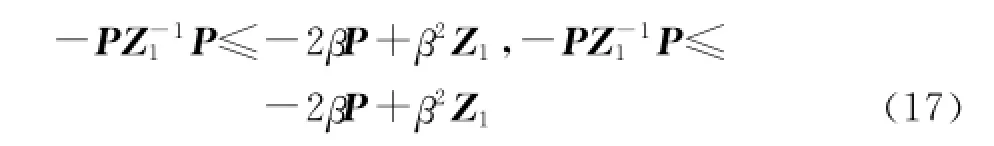
将式(16)作PG=V替换，并将式(17)代入，即得V·≤ξT(t)Φξ(t).

若存在正定对称矩阵P，Q1，Q2，Z1，Z2使Φ≤0成立，则V·≤0.

注2由于事件发生器置于控制器之后，故系统的测量输出和故障诊断观测器的输出残差不受触发条件的影响，进而使观测器的设计过程大大简化.

2　混合容错控制器的设计

首先设计被动容错控制器，使得执行器在无故障、发生故障集以内故障或其他未知故障初期时，能够确保系统稳定.同时故障诊断观测器对故障进行检测和分离，一旦获得准确的故障信息就重构控制器.然后将重构的控制器切换到线性NCS中，以保证系统不但稳定而且具有较好的控制性能.

2.1被动容错控制器的设计

PFTC设计的目标：针对闭环故障系统式(5)求取适当的状态反馈增益阵KP，使得闭环系统在可能的执行器失效故障下渐进稳定.

定理2给定正数τm，τM，τs，δ，δ∈0，[)1，若存在正定对称矩阵X，Y，V以及Ri>0，i=1，2，…，5，对可能的执行器失效故障，满足线性矩阵不等式

则基于事件触发的闭环故障NCS式(5)渐进稳定，且控制器增益可通过KP=YX-1求取，触发矩阵Φ =V-1.式中：*表示由矩阵的对称性得到的矩阵块，而

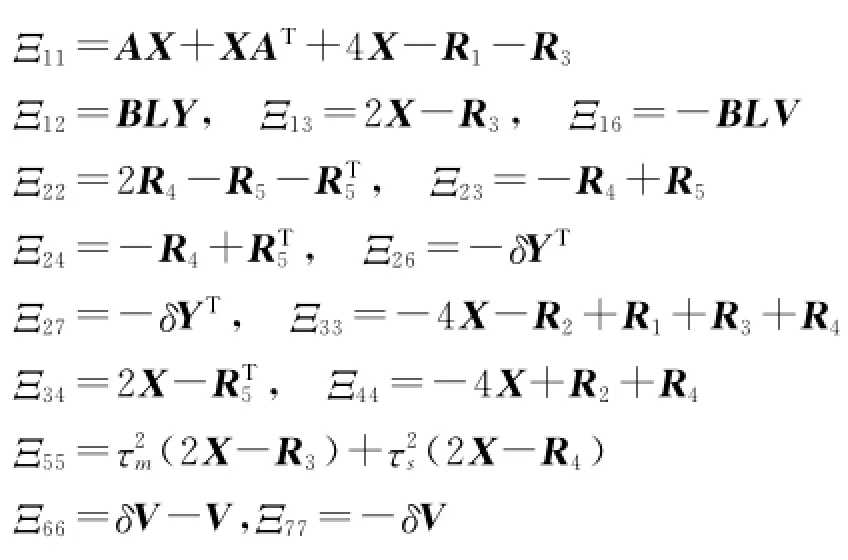
证明构造Lyapunov-Krasovskii泛函

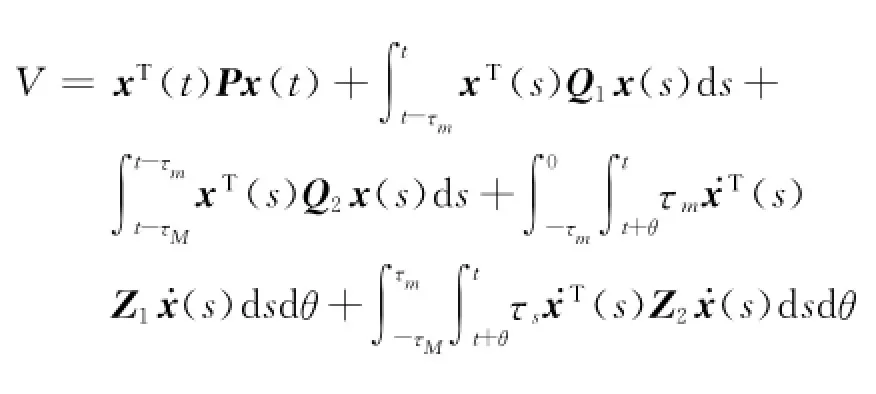
设

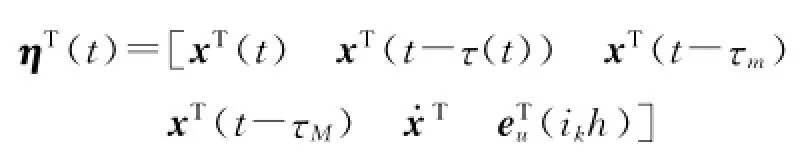
沿着式(5)，对V两边求导

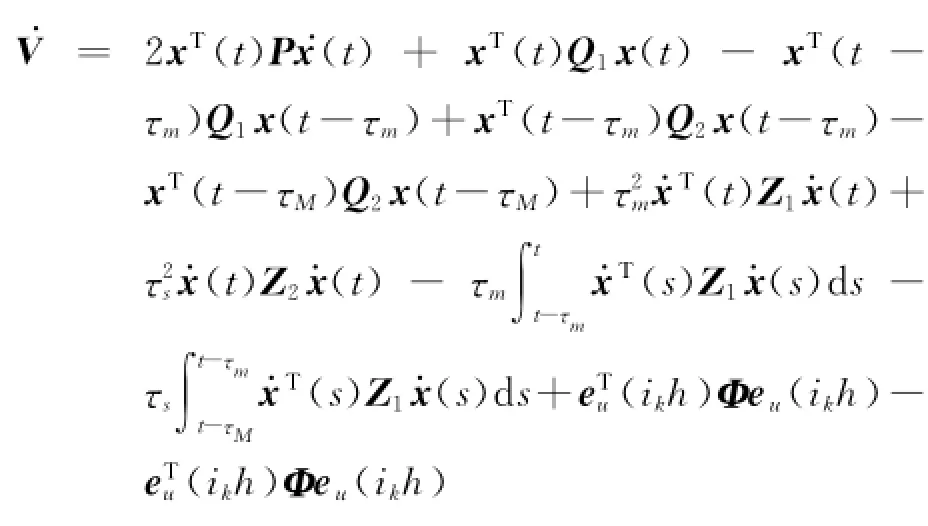
其中，由式(1)的

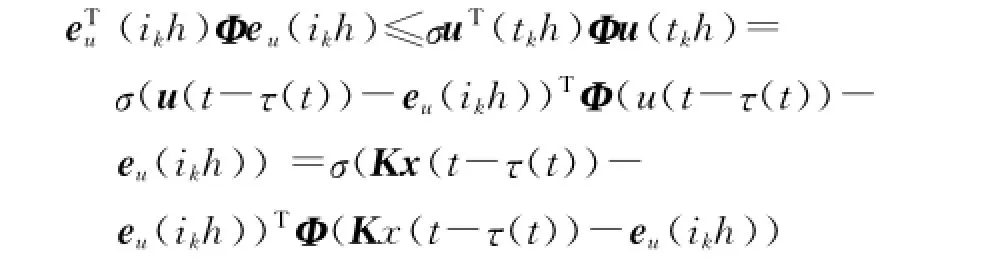
证明同定理1.综合引理1和式(1)，得V·≤ηT(t)Ξ′η(t)

式中：

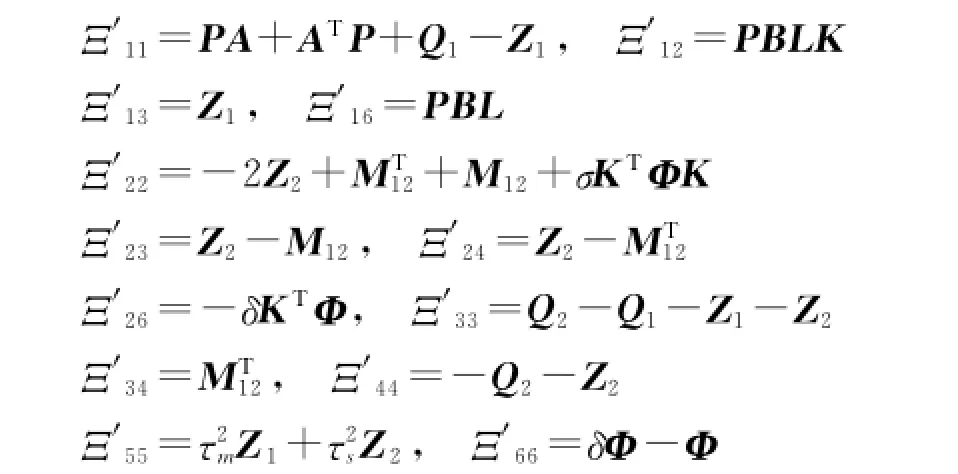
由于Ξ′中含有非线性项，不等式不好求解，所以由shur补得

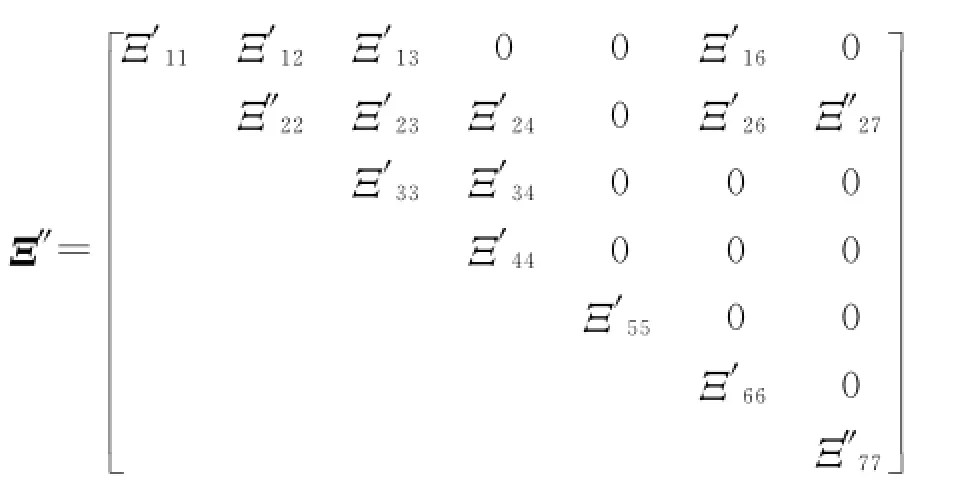
式中：Ξ″22=-2Z2+MT12+M12；Ξ″27=σKTΦ，Ξ″77= -σΦ.

在Ξ″两边同时乘以

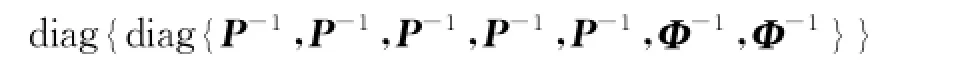
在Ξ″两边同时乘以令X=P-1，KX=Y，Φ-1=V并参照文献[16]做如下变换：

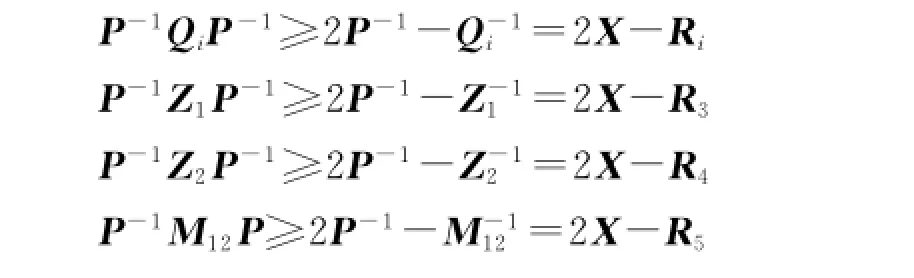
即可得到Ξ，若存在正定对称矩阵X，Y，V，Ri(i =1，2，…，5)使得Ξ≤0即式(18)成立，则V·≤0，且KP=K=YX-1.定理2证毕.

2.2主动容错控制器的设计

AFTC设计的目标.假定f^(t)=f(t)，代表正确的故障估计值，此时相应的补偿控制器定义为式中，KN为系统正常工作时使系统性能达到最优的控制反馈增益.

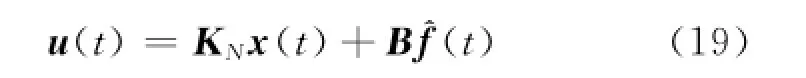
定理3考虑带有故障的闭环系统式(5)，给定正数τm，τM，τs，δ，δ∈0，[)1，若存在正定对称矩阵X，Y，V以及Ri>0，i=1，2，…，5，满足线性矩阵不等式

则存在控制器增益KN=YX-1使得系统在执行器故障时稳定且性能最优.

式中：

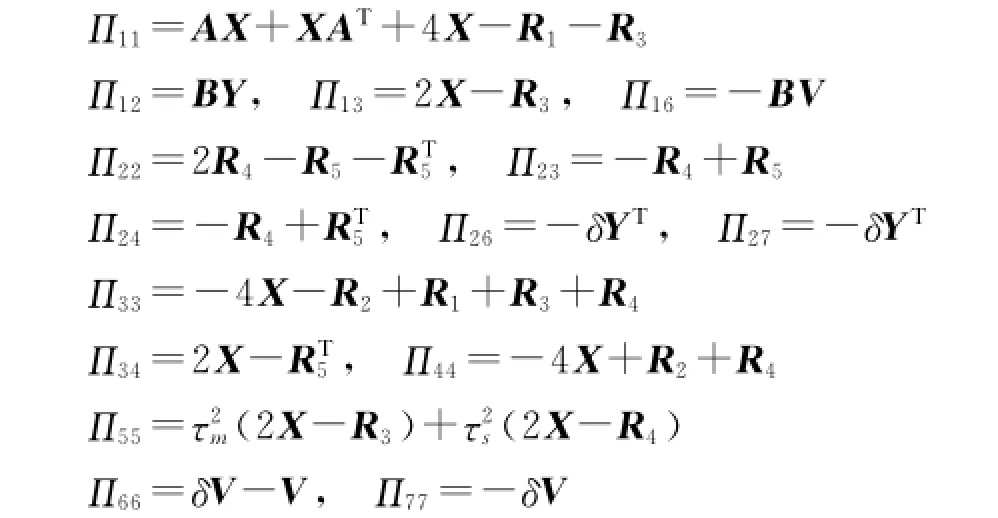
证明过程与定理2相似，此处略.

3　仿真结果

考虑线性NCS，采用文献[8]中的模型数据：

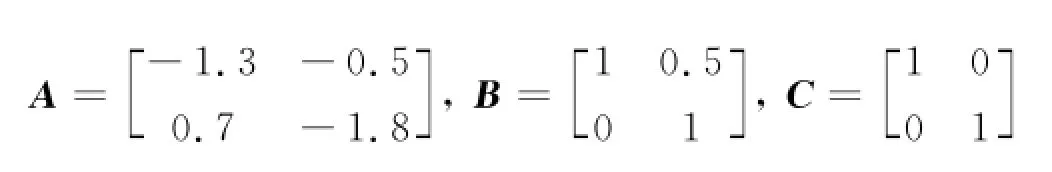
设L1、L2分别为执行器正常和发生故障集内部分失效故障，取

假设系统运行至5 s时执行器发生L2故障，运行至9 s时执行器发生故障集外故障，即

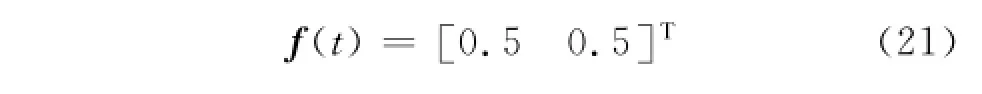
采样周期为h=0.05 s，τm=0.1，τM=0.4则τs =0.3.取参数α=0.2，β=0.4，δ=0.2.

3.1控制器增益的求解

首先由定理2求出被动容错控制器增益KP和触发矩阵Φ

取相同的参数由定理3求出主动容错控制器KN，由定理1求出观测器增益G、输出误差矩阵W 3.2对比被动、主动，主被动混合容错控制效果

3.2对比被动、主动，主被动混合容错控制效果

图2所示为故障估计值f(t)与故障输入值f(t)的效果图.由图可见，在5 s和9 s时估计值f^(t)比故障信号略有滞后，但最终完全跟踪.

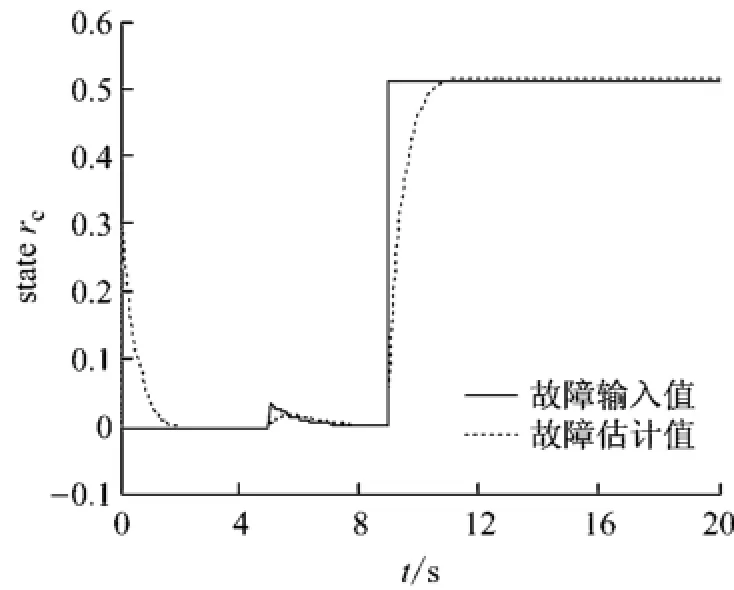
图2　故障估计曲线图Fig.2　Estimation curve of fault

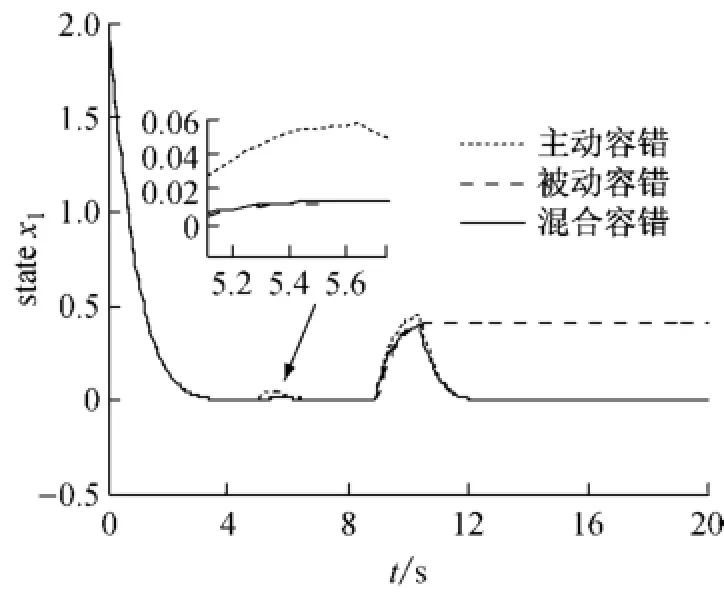
图3　闭环系统状态x1响应曲线图Fig.4　Response curve of state x1of closed-loop model

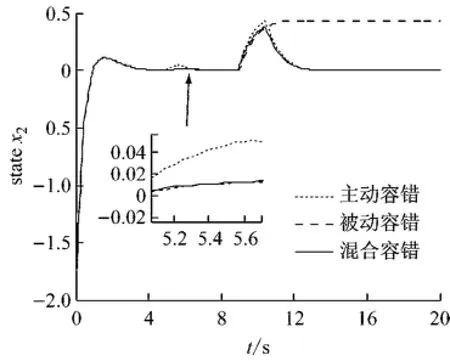
图4　闭环系统状态x2响应曲线图Fig.4　Response curve of state x2of closed-loop model

由图可见，在最初执行器正常时，AFTC和PFTC都可以使系统稳定；当发生故障集以内故障时，PFTC始终保持系统稳定而AFTC需要一定的故障诊断和重构控制器的时间后才保持系统稳定；当发生故障集以外的故障时，PFTC虽对故障有一定的抑制作用，但最终无法确保系统稳定.AFTC经过正确故障诊断及重构控制器后补偿了故障的影响.由对比可见，主被动混合容错结合了PFTC和AFTC各自的优点，在发生执行器任意失效故障下都可以保持系统稳定且具有一定的控制性能.

为说明加入事件发生器确实节约了部分网络资源，对于采样周期h=0.05 s，δ=0.2时，取20 s的仿真时段，通过统计得实际发送数据159个，若采用时间触发方式则数据发送量应为400个，可见与时间触发通信相比事件触发通信机制下NCS确实有效节约了网络资源.

4　结　语

本文针对一类具有时变时延的线性NCS，在引入事件触发机制的条件下，针对执行器故障进行了主被动混合容错控制的研究.首先利用被动容错控制的优点保证系统在发生故障集以内故障时稳定，并有效抑制故障集以外故障造成的性能恶化速度.同时利用故障诊断观测器估计故障大小，获得准确的故障信息后重构控制器，然后由切换开关将重构控制器切换到系统中以补偿任意执行器失效故障，使得系统不但稳定而且保持良好的控制效果.整个过程在保证系统控制性能和节约网络资源的前提下实现了PFTC和AFTC的有效结合，数值仿真算例显示了所提方法的有效性.

[1]Zhang Yuyan，Zhang Junling，Luo Xiaoyuan.Sensor/actuator faults detection for networked control systems via predictive control[J].International Journal of Automation and Computing，2013，10(3)：173180.

[2]Li S B，Dominique S，Christophe A，et al.Stability guaranteed active faulttolerant control of networked control systems[J].Journal of Control Science and Engineering，2008，8(1)：3342.

[3]Tahoun A H，Fang H.Adaptive stabilization of networked control systems tolerant to actuator failures [C]//International Conference on Information Technology and Computer Science.Beijing：IEEE，2009，2：535539.

[4]胡松林.基于事件触发机制的网络化控制系统的分析与综合[D].湖北：华中科技大学，2012.

[5]齐晓妹.网络控制系统的鲁棒故障检测与容错控制方法研究[D].山东：山东大学，2012.

[6]李炜，王艳飞.少保守性网络化控制系统鲁棒保性能容错控制[J].兵工学报，2012，33(2)：170178.

[7]Mao Zehui，Jiang Bin.Fault estimation and accommodation for networked control system with transfer delay[J].Acta Automatica Sinica，2007，33(7)：738743.

[8]赵莉.基于离散事件触发的NCS鲁棒容错控制研究[D].甘肃：兰州理工大学，2014，6.

[9]Peng Chen，Yang Taicheng.Eventtriggered communication and H∞control codesign for networked control systems[J].Automatica，2013，49(5)：13261332.

[10]Liu Jinliang，Yue Dong.Eventtriggering in networked systems with probabilistic sensor and actuator faults[J].Information Sciences，2013，240(10)：145160.

[11]Yu Xiang，Jiang Jin.Hybrid faulttolerant flight control system design against partial actuator failures [J].IEEE Transactions on Control Systems Technology，2012，20(4)：871886.

[12]金小峥，杨光红，常晓恒，等.容错控制系统鲁棒和自适应补偿设计[J].自动化学报，2013，39(1)：3142.

[13]Xia H W，Ma G C，Wang C H，et al.Fault detection filter design for networked control systems with networkedinduced delay[C]//IEEE Conference on Industrial Electronics and Applications，2007.Harbin，China：IEEE，2007：10231026.

[14]Jiang X F，Han Q L，Liu S R，et al.A new stabilization criterion for networked control systems[J]. IEEE Transactions on Automatic Control，2008，53(4)：10251032.

[15]PooGyeon Park，Jeong Wan Ko，Changki Jeong.Reciprocally convex approach to stability of systems with timevarying delays[J].Automatica，2011，47 (1)：235238.

[16]董全超.线性时滞系统鲁棒H∞故障估计与主动容错控制[D].山东：山东大学，2010.

(编辑俞红卫)

Design of Hybrid FaultTolerant Networked Control System Based on EventTriggered ScheMäe

WANG Jun，LI Shuzhen，LI Wei
(College of Electrical and Information Engineering，Lanzhou University of Technology，Lanzhou 730050，China)

Aiming at a networked control system(NCS)with timevarying delay，under the eventtriggered communication scheMäe，a hybrid faulttolerant control system(FTCS)combining the Mäerits of passive and active FTCSs was proposed to accommodate actuator failures.Closedloop failure model of networked control system was established.The design of PFTCS could guarantee the stability of the system under the small faults or the failure within the known fault set.The fault diagnosis observer could detect and estimate the faults at the saMäe time.Once the correct fault information was obtained，the AFTCS could compensate for the effect of actuator faults.The hybrid faulttolerant could compensate all the actuator failures.An example was given to demonstrate that the proposed approach could save network communication resources on the premise of making sure failure system was stable.

networked control system(NCS)；eventtriggered communication scheMäe；hybrid faulttolerant control system；fault diagnosis observer

TQ 302.8

A

16717333(2015)02017807

10.3969/j.issn.16717333.2015.02.016

2015-01-14

王君(197-)，女，副教授，博士，硕士生导师，主要研究方向为故障诊断与容错控制.E-mail：wangj31901@163.com