飞机纵向姿态传感器故障鲁棒容错控制

丁润泽，　肖玲斐，　姜　斌

飞机纵向姿态传感器故障鲁棒容错控制

丁润泽a，肖玲斐a，姜斌b

(南京航空航天大学a.能源与动力学院；b.自动化学院，南京210016)

通过研究飞机纵向受力，建立了飞机在高空定速巡航过程的纵向运动模型.针对飞行过程中可能出现的传感器故障和系统参数摄动，考虑跟踪控制问题，利于跟踪误差对系统模型进行增广，在构建状态观测器的基础上，设计了飞机纵向姿态传感器故障鲁棒容错控制器.仿真结果表明，当传感器发生故障时，飞机系统能够迅速稳定，具有满意的稳态和动态性能以及良好的鲁棒性.

飞机纵向姿态；传感器故障；容错控制；状态观测器

飞机作为大型战略型高技术装备，其研制兼有政治、经济、技术多重意义，不仅能反映一个国家的能力，而且具有巨大的市场盈利空间，同时对技术、产业的发展有着巨大的牵引力，其研制必将有力地拉动中国的技术进步和产业升级，强化民族工业力量[1].飞机是一个复杂的多自由度系统，能够稳定、准确地控制飞机的姿态是十分必要的.飞控系统是飞机的灵魂，其安全性和可靠性是控制器设计的一个关键问题，它能避免飞行和人身安全受到故障的影响和威胁[2-3].由于控制系统非常复杂，因此，对控制性能要求更高，对其各部件的可靠性、准确性要求也越来越高，而飞机在恶劣的工作环境下，传感器更容易出现故障，控制系统发生故障的概率也随之增加[1-3].传感器、执行机构或系统的故障都可能彻底地改变系统行为，导致系统性能下降，甚至不稳定，一旦发生故障，如果不及时进行有效的容错处理，极有可能造成人员和财产的巨大损失.很多飞行事故的调查结果发现，在飞控系统出现故障时采取适当的措施能够避免事故的发生[4].因此增强控制器的鲁棒性，采取容错控制是飞机控制领域必须解决的问题之一[5].

本文通过分析飞机受力，建立飞机在高空定速巡航的数学模型，并针对此模型建立带有状态观测器的飞机纵向姿态控制器，通过燃油和舵面角度控制飞机的欧拉角，并对可能出现的系统参数摄动和传感器故障进行了鲁棒性容错控制研究.

1　飞机纵向运动受力分析

以B707飞机纵向运动为例，飞机受力分纵向气动力和力矩[6-7].

在飞行过程中由于上下压差产生升力，包括：机翼升力CAW，机身升力CAb，平尾升力CAWW.升力主要受机翼的攻角，平尾升力还同时受到舵面偏角影响.因此整机升力可表示为：式中：q-为动压；S为机翼面积；α为气流攻角；η为舵面偏角.

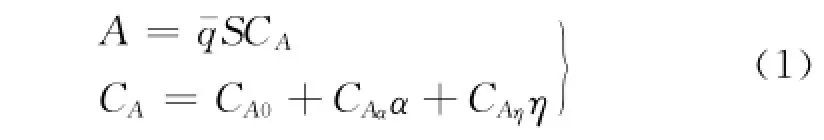
在飞行过程中气流作用于物体表面的法向力及气流对物体表面的切向摩擦力，由于空气具有黏性，故在飞行过程中，飞机受到不受升力影响的摩擦阻力，即零升阻力.由于翼型前缘高压区与后缘低压漩涡区，形成向后的压力差，机翼前缘顺压梯度，速度增大，在机翼后缘速度逐渐减小到零，附面层分离产生压差阻力，形成升致阻力.亚声速飞行时，飞机在翼尖形成自由涡和下洗角，升力有了向后的分力，产生由升力导致的诱导阻力.

于是整机阻力可表示为

飞机受到的力矩主要为作用于飞机的外力产生的绕机体Oy轴的力矩以及发动机推力T产生的力矩.因此影响气动力的因素，即为影响气动力矩的因素，除此之外，当俯仰角速度q≠0时，平尾向下运动使气流有相对向上的速度，局部迎角变大，增力变大，产生由飞机俯仰引起，作用方向为阻止飞机俯仰的阻尼力矩.

整机俯仰力矩可表示为

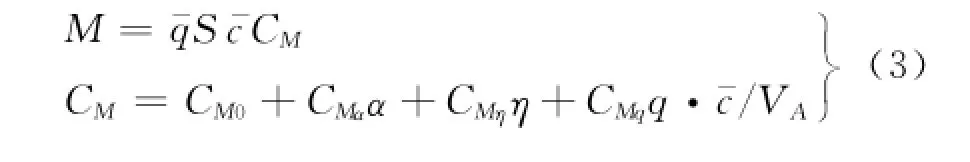
2　飞机纵向运动控制模型

由飞行动力学知识[8-9]可得飞机纵向运动方程如下：

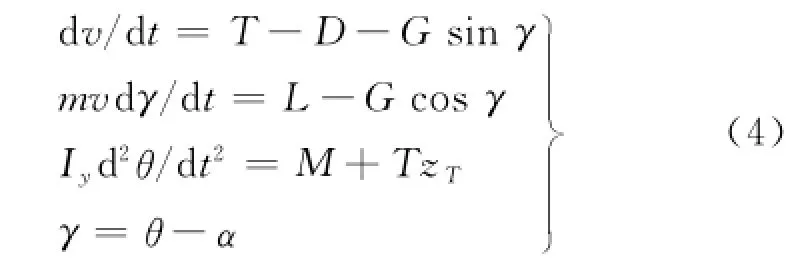
式中：v为飞行速度；D为阻力；T为推力；Iy为飞机绕y轴转动惯量；θ为欧拉角；γ为航迹角；α为攻角；zT为推力夹角.由上述飞机受力分析可知：

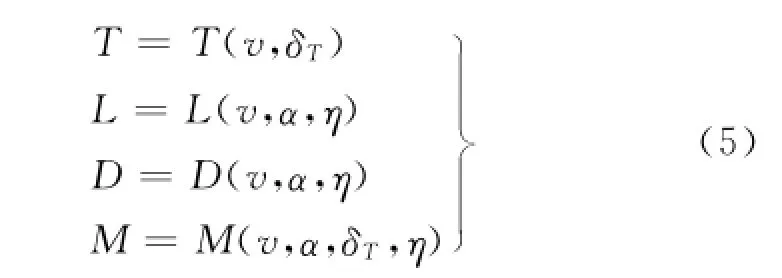
式中：L为升力；δT为俯仰舵面偏角；η为偏航舵面偏角.

将各式泰勒展开，忽略高阶项后可得

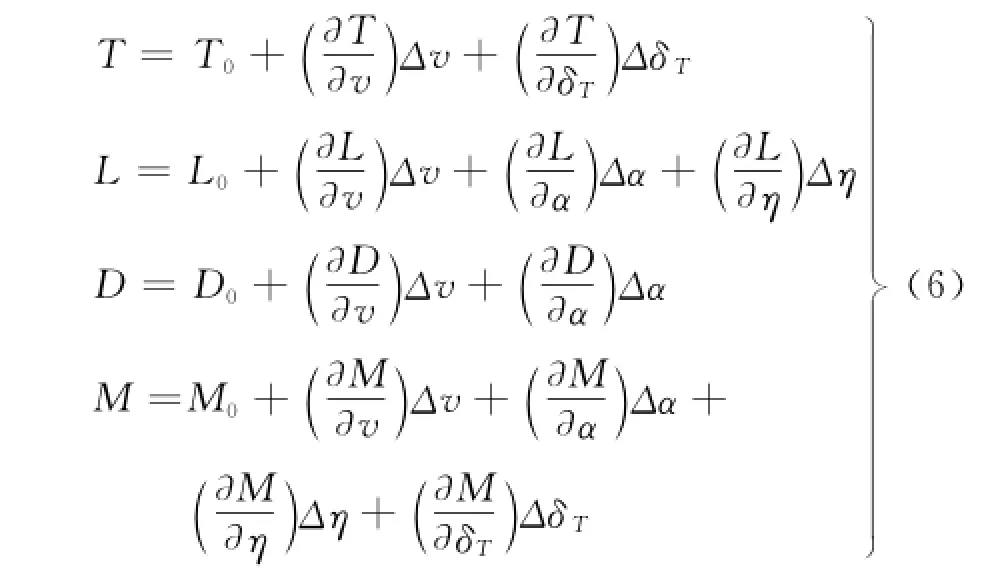
即

整理为状态空间模型：

即

式中：

其中：S为机翼面积；c为平均气动弦长；b为翼展；m为飞机质量；I为惯性矩；Tmax为发动机最大推力；ρ0=1.225 kg/m3；H为飞行高度；q为俯仰角速度；输入量为油门角度δT和舵面偏角η.

3　传感器故障鲁棒容错控制器设计

飞机在实际飞行控制系统中，系统不可避免存在参数不确定，并且有可能使传感器发生故障.针对这些情况，设计出具有良好鲁棒性的飞机传感器容错控制器.飞机传感器故障鲁棒容错控制系统结构如图1所示.

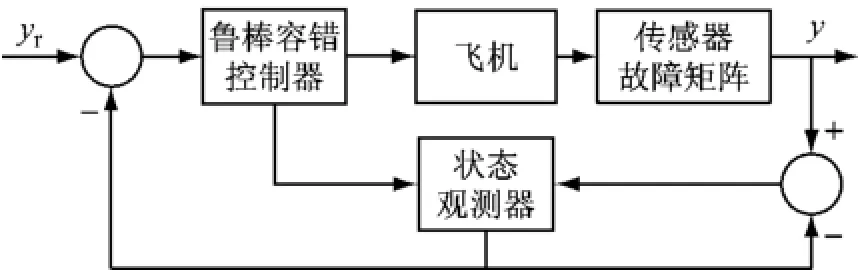
图1　飞机传感器故障鲁棒容错控制系统Fig.1　Aircraft sensor fault robust fault tolerant control system

针对带有状态观测器的系统设计控制器，用传感器故障矩阵来表示传感器故障.当不考虑传感器故障时，设计状态观测器系统为观测误差系统为

观测误差系统为

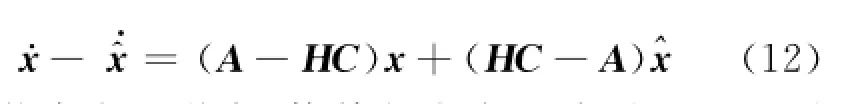
将原来状态向量增广，使其包含有跟踪误差和观测误差.

结合式(11)、(12)，有

考虑跟踪误差e=x-xr，其中期望状态量xr满足x·r=Arxr+Brur，则

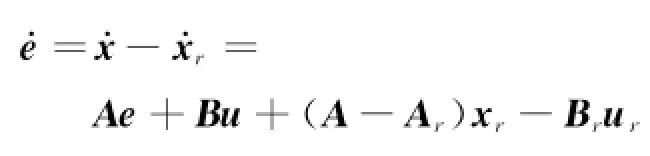
当(A-Ar)xr-Brur=0时，有e·=Ae+Bu.则式(13)可变为

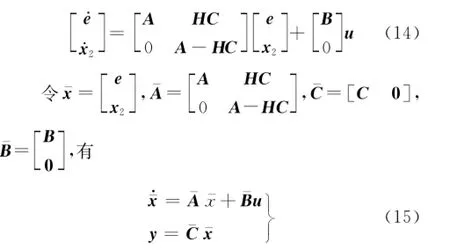
对增广后的系统进行控制器设计以达到在控制器的作用下同时消除跟踪误差和观测误差的目的.

假设系统式(15)存在摄动

其中摄动满足：

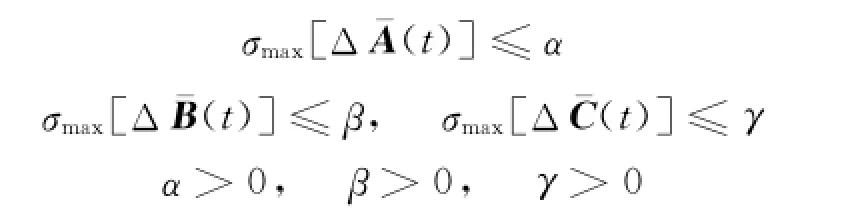
则闭环方程可表示为：

定义Riccati方程为

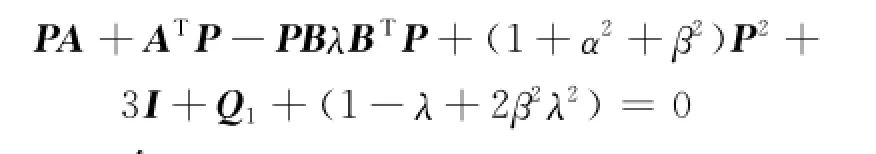
令

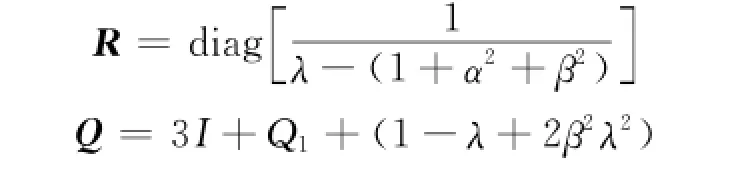
根据最优控制原理，采用最优性能指标

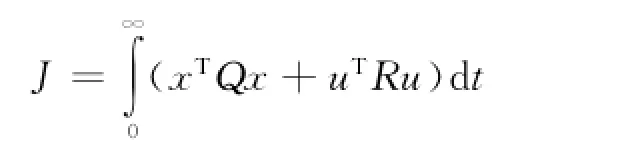
可得控制律为

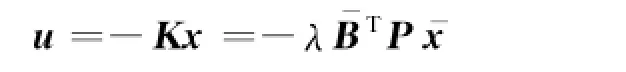
考虑传感器失效矩阵[7]

F=diag{σ1，σ2，…，σm}，0≤σi≤1，i=1，2，…，m σi为第i个传感器失效度.当σi=1表示传感器正常，σi=0表示完全失效，0<σi<1表示部分失效.

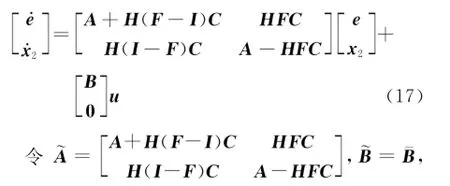
此时式(14)变为，则式(17)可写为

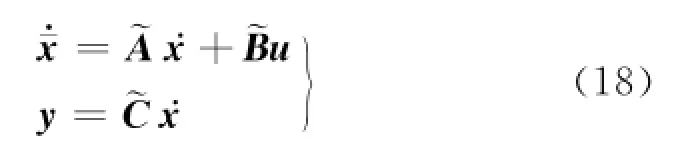
同理，可针对系统式(17)设计鲁棒容错控制律，以使飞机在飞行过程中受到扰动时能够迅速稳定，不偏离预定航线，并对可能存在的传感器故障和参数摄动具有鲁棒性的目的.

4　仿真结果

对于式(9)，代入B707飞机的数据：S=268 m2，c-=6.39 m，b/2=21.7 m，m=1×105 kg，Ix= 5.03×106 kg·m2，Iy=6.87×106 kg·m2，Iz= 12.26×106 kg·m2，Ixz=0 kg·m2，Tmax=320.8 k N，zF=-1.5 m，iF=0°，CA0=0.239，CAα=4.60，CAη=0.189，CD0=0.018，CDα=0.103，CDη= -0.011，CM0=0.070，CMα=-0.824，CMα·= -3.63，CMq=-8.97，CMη=-0.638.可得飞机纵向运动方程

不难判断，系统是可观的选取状态观测器的零点在-1，-2，-3，-4上，则由

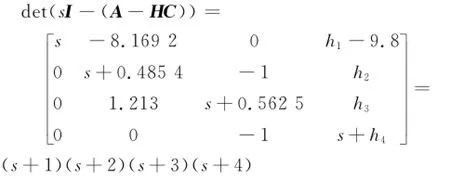
得H=[0-20.61624.1348.952 1]T.

对系统进行增广，可得

假设系统存在不确定项：ΔA=0.1×A，ΔB=0.1× B，ΔC=0.1×C，取Q=3.545 0×I8×8，R=2.222 0 ×I2×2，得反馈矩阵

当考虑失效矩阵后

假设期望输出量yr=1，初始时无传感器故障，在5 s时传感器出现故障，故障矩阵F=0.5.仿真结果如图2～4所示.

由图可知，系统能够尽快地稳定，并具有可接受的性能，对系统参数摄动具有鲁棒性.在传感器出现故障时，系统出现波动，采用容错控制律后，系统能够迅速重新稳定.由图4可发现跟踪信号能够迅速跟踪上期望信号，并在系统发生故障时，迅速稳定重新跟踪上期望信号.

图2　纵向姿态角响应曲线Fig.2　Response curve of longitudinal attitude

图3　舵面偏角控制量Fig.3　Rudder angle control signal

5　结　语

本文通过研究飞机纵向受力和运动，建立了飞机在高空定速巡航过程的纵向运动控制模型.考虑飞行过程中可能出现的传感器故障和系统参数摄动，设计了带有状态观测器的飞机纵向姿态传感器故障鲁棒容错控制器.仿真结果表明，当传感器发生故障时，飞机系统能够迅速稳定，具有满意的稳态和动态性能以及良好的鲁棒性.参考文献：

[1]许域菲.近空间飞行器非线性容错控制技术研究[D].南京：南京航空航天大学，2011.

[2]高志峰.复杂系统的容错控制技术及其在近空间飞行器中的应用研究[D].南京：南京航空航天大学，2011.

[3]李怡勇，沈怀荣，李岩.先进控制方法在飞行控制系统设计中的应用[J].飞航导弹，2006，35(12)：5054.

[4]张新国，张汝麟，陈宗基.飞行控制系统设计方法研究[J].航空科学技术，1997，8(1)：1719，31.

[5]Kung C.Nonlinear H∞robust control applied to F16 aircraft with mass uncertainty using control surface inverse algorithm[J].Journal of the Franklin Institute，2008，345(6)：851876.

[6]苗德乃.飞机建模与控制仿真[D].北京：北京航空航天大学，2003.

[7]黄书鹏，王诗宓.带状态观测器系统的鲁棒容错控制[J].控制理论与应用，2001，18(2)：249252.

[8]谭珍珍.大型民机飞行控制系统建模仿真研究[D].南京：南京航空航天大学，2014.

[9]张剑，谢刚涛，余圣晖，等.民用飞机线性化仿真分析[J].航空科学技术，2014，25(5)：6366.

(编辑俞红卫)

Robust Fault Tolerant Control for Aircraft Longitudinal Attitude Sensor Faults

DINGRunzea，XIAO Lingfeia，JIANG Binb
(a.College of Energy and Power Engineering；b.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

Based on the study of aircraft longitudinal stress and motion，the mathematical model of an aircraft longitudinal position in highaltitude cruise process was constructed.Aiming at possible sensor faults and parameter perturbation，and taking the tracking control problem into account，the model of system was extended by using tracking error.Based on the construction of the state observer，a robust fault tolerant controller for aircraft longitudinal position sensor faults was obtained.Simulation results showed that when the parameter perturbation and sensor faults took place，the system could attain prompt stability with satisfying dynamic，steady performance and superior robustness.

aircraft longitudinal attitude；sensor faults；fault tolerant control； state observer

V 24

A

16717333(2015)02016706

10.3969/j.issn.16717333.2015.02.014

2015-01-15

中央高校基本科研业务费专项基金资助项目(NJ20140022)；国家商用飞机制造过程技术研究中心创新基金资助项目(SAMC14JS15053)

丁润泽(1993-)，男，硕士生，主要研究方向为飞机及动力系统控制.E-mail：1822784299@qq.com

肖玲斐(1982-)，女，副教授，博士，硕士生导师，主要研究方向为控制系统建模与优化、故障诊断与容错控制. E-mail：lfxiao@nuaa.edu.cn