一类多角形的内角和

邵雷雷

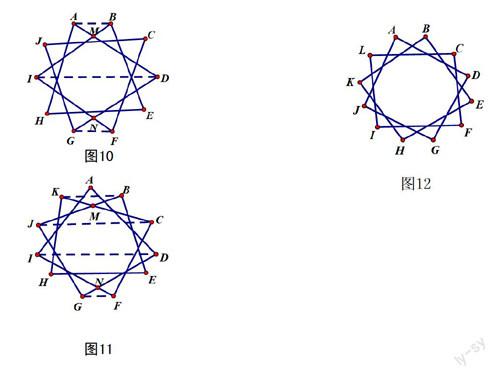
在平面图形中，有一些由平面上分布的某些点每隔一个或几个顺次连接构成的图形，由于类似星形，我们可以把它称作N角星，这些N角星的内角和呈现非常有规律的变化。

以常见的五角星为例（如图1）平面上分布的五个点A、B、C、D、E，从A点出发，每次隔一个点，按A-C-E-B-D-A的顺序依次连接，形成了类似五角星的图案，由于每次相隔一个点进行连接，我们称之为第一类五角星，∠A+∠B+∠C+∠D+∠E的度数为第一类五角星的内角和。图1中，∠AMN=∠B+∠D，∠ANM=∠E+∠C， ∠A+∠B+∠C+∠D+∠E=∠AMN+∠ANM+∠A=180°。所以，第一类五角星的内角和为180°。

第一类六角星（如图2），是由两个三角形组合而成的图形，所以其内角和为180°×2=360°。

第一类七角星（如图3），由平面内七个点按A-C-E-G-B-D-F-A顺次连接，连接BF、CG，∠AMN=∠MFB+∠MBF，∠ANM=∠NGC+∠NCG，那么第一类七角星的内角和被分解为三个三角形△AMN、△GEC和△BDF的内角和之和，所以第一类七角星的内角和等于180°×3=540°。

第一类八角星（如图4），是两个四边形组合而成的图形，所以其内角和为360°×2 =720°。

图1

图2

图3

图4

图5

图6

第一类九角星（如图5），连接BH和CI，∠AMN=∠MHB+∠MBH，∠ANM=∠NIC+∠NCI，所以九角星的内角和可以分为两个四边形HFDB和IGEC，再加一个三角形△AMN的内角和之和，即为360°+360°+180°=900°。

第一类十角星（如圖6），是由两个五边形组合而成的图形，其内角和为：540°×2=1080°。

综上可知，第一类N角星（N≥5）的内角和有如下的规律：当N为奇数时，其内角和可以分为两个边形加上一个三角形，所以其内角和应为：

当N为偶数时，其为两个边数为的多边形组成的，其内角和应为：（-2）×180°×2=（N-4）×180°。所以，第一类多边形的内角和是（N-4）×180°，（N≥5）。

还有第二类N角星，在平面上分布的N个点，如果每隔两个点连接为一条边，构成的图形我们可以称为第二类N角星，第二类N角星的内角和有什么规律呢？

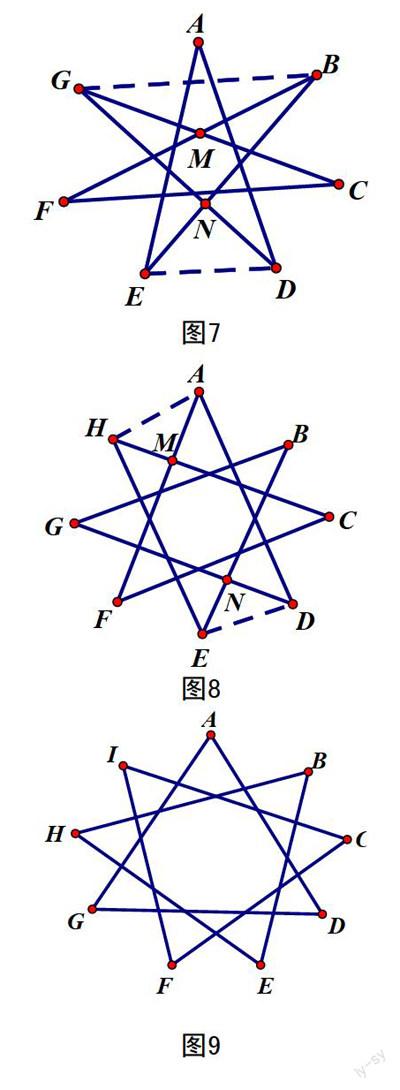
第二类多角星至少为7个角（如图7），平面上分布的七个点，每次相隔两个点，按照A-D-G-C-F-B-E-A的顺序依次连接，得到的图形为第二类七角星。连接BG、DE，易知    ∠F+∠C=∠MGB+∠MBG，∠NGB+∠NBG= ∠NED+∠NDE，所以第二类七角星的内角和就转化为△AED的内角和，为180°。

第二类八角星（如图8），连接AH、ED，易知∠F+∠C=∠MHA+∠MAH，∠B+∠G=∠NED+∠NDE，所以第二类八角星的内角和转化为四边形AHED的内角和，应为360°。

图7

图8

图9

图10

图11

图12

第二类九角星（如图9），是由三个三角形组合而成的图形，所以其内角和应为180°×3=540°。

第二类十角星（如图10），连结AB、ID、GF，易知∠MID+∠MDI=∠MAB+∠MBA，      ∠NID+∠NDI=∠NGF+∠NFG，所以第二类十角星的内角和被转化为两个四边形AHEB和JGFC的内角和之和，所以其内角和应为360°×2=720°。

第二类十一角星（如图11），连结BK、JC、ID、GF，易知∠MJC+∠MCJ=∠MKB+∠MBK，∠NID+∠NDI=∠NGF+∠NFG，第二类十角星的内角和被分为两个四边形KHEB和JGFC，以及一个△AID，其内角和为360°×2+180°=900°。

第二类十二角形（如图12），是由三个四边形组成的图形，其内角和为360°×3=1080°。

综上所述，第二类N角星（N≥7）的内角和可以推测满足表达式：（N-6）×180°。