基于近邻传播聚类的卫星典型构件典型工艺过程发现
2015-07-25张永健钟诗胜
王 琳,张永健,钟诗胜
(1.哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨 150001;2.哈尔滨工业大学(威海)船舶与海洋工程学院,山东 威海 264209)
0 引言
一般而言,企业在对产品进行工艺规划时都是参照原有的工艺过程,而随着企业的不断发展,积累了大量的工艺数据,这些工艺数据可以作为企业的知识资源。如何挖掘这些知识并对其进行有效利用,是大规模定制(Mass Customization,MC)生产模式在企业制造端成功实施的关键。典型工艺过程是企业为典型产品(典型零件或部件)制定的普遍适用的工艺过程,在对与该典型产品相似的产品进行工艺规划时,可借用该过程并对其进行适量修改,即可作为新零部件的工艺过程,以此提高产品工艺规划的效率与质量。
对于典型工艺过程的获取,目前国内外的相关研究主要集中在工艺过程的相似性和聚类分析等方面。文献[1]用工艺路线间的距离来衡量工艺路线的相似度,并采用凝聚层次聚类算法实现工艺路线的聚类划分;文献[2]将最长相似子序列作为度量因子,对工艺路线进行多级相似度综合度量,并采用粒子群优化算法实现了工艺路线的智能聚类划分;文献[3]通过建立基于特征的零部件信息模型,研究了基于实例推理的工艺相似性度量。这些研究主要对工艺序列的相似性和聚类问题给出了较好的解决方案,但是工艺过程的相似性度量方法仍不理想,另外受各工序与产品特征和车间资源之间存在相关性、工艺过程表达的规范性等因素的影响,计算结果与实际情况往往偏差较大。因此,需要通过建立工艺过程的数学模型,以提高其相似性的计算精度。
为提高工艺设计的效率,并对工艺规划过程进行优化,将图论引入工艺规划的研究中。文献[4]提出用一般图对工艺规划进行描述的方案;文献[5-6]通过装配关系的特征,采用(加权)有向图对装配工艺建立描述模型;文献[7]采用有向图对数控工艺中的机床工作计划进行数学描述;文献[8]为实现零件工艺的聚类,基于加权有向图建立了零件工艺的描述模型,将工艺聚类问题转化为有向图的聚类问题。有向图在社会网络和信息网络等方面应用广泛,而与此相关的有向图聚类的研究成果较为丰富,如欧拉距离、曼哈顿距离、余弦相似度、基于Jaccard指数的相似度量等方法在有向图顶点的相似性度量方面应用广泛[9];属性图能够对复杂网络进行有效描述,邻域随机游动距离、Bayesian随机模型等为属性图的聚类提供了可行方案[10-12]。
典型工艺过程发现技术是在历史工艺过程数据中,利用数据挖掘技术,对大量的工艺过程进行分析,研究工艺过程中工艺单元之间的关系,获取工艺过程所具有的共性,从而获得典型工艺过程的方法。本文采用属性有向图对工艺过程进行描述,通过工艺过程属性有向图结构与属性相似度的计算来提高工艺过程相似性的计算精度;基于工艺过程的相似性,采用近邻传播算法发现典型工艺过程。
1 典型工艺过程发现问题的数学模型
1.1 基于属性有向图的工艺过程描述模型
在有向图结构中,节点表示对象,每条边都有方向,表示对象之间的关系。本文各节点包含不同的属性描述信息,因此,首先给出以下定义。
定义 属性有向图。属性有向图可表示为一个四元组G=(V,E,A,F),其中:V为M个节点的集合,E={(vi,vj)|1≤i,j≤M,i≠j}为有向边的集合,A={a1,a2,…,aL}为V中节点的L种分类属性的集合。每个节点vi的属性可用长度为L的属性向量p(vi)=[a1(vi),a2(vi),…,aL(vi)]进行描述,其中aj(vi)为节点vi在属性aj上的观测值。F={f1,f2,…,fL}为L个函数的集合,其中fi:V→D(ai)为指定某节点vi的属性ai在其值域D(ai)中的取值。
一个工艺过程通常由一组工序经过有序排列构成,而由于工艺种类的差别或工艺编制人员习惯的不同,导致工艺过程中工序的表达与层次划分千差万别。为便于工艺过程属性有向图模型的建立,在此定义工艺过程由一组工艺单元构成,其中工艺单元是指针对产品的某制造特征采用何种设备完成的特定操作。给定一组工艺单元集合,作为工艺规划时工艺单元的选择空间Sp,工艺规划可以描述为在符合产品技术要求及工艺原理的条件下,Sp中的全部或部分工艺单元按照一定的顺序进行排列。工艺过程可以用属性有向图进行建模,其中属性有向图G中的节点集V表示工艺过程的工艺单元集,V中的每个元素可以用属性向量进行描述,即

式中:pn为工艺单元名称;pf为工艺单元所对应的产品特征;pm为产品特征的关键制造信息(制造特征参数);po为产品特征所对应的制造方法;pe为产品特征所对应的设备;pr为产品特征所对应的制造技术要求。
属性向量中的各属性值由函数集合F中相应的函数指定,有向边集E表示工艺过程中工艺单元的操作顺序。某类零件工艺过程可以用如图1所示的有向图模型表示,图中虚线表示该类零件可以由两种工艺过程实现其加工,因此,工艺过程的有向图模型即为有向无环图中最简单的线性图。
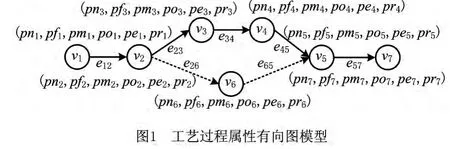
给定两个工艺过程Gα和Gβ,两者的相似度表示为S(Gα,Gβ),可以由工艺单元相似度SN(Gα,Gβ)和工艺路线相似度SS(Gα,Gβ)加权获得,即

式中ω为加权系数,0≤ω≤1。
1.2 工艺过程有向图模型中相似度算法
1.2.1 工艺单元相似性
对相似产品(包括零部件)而言,其工艺过程一般具有相似性,但在具体产品进行工艺规划时,相似产品的工艺过程所包含的工艺单元的数量难以保证相同;即使工艺单元数量相同,各对应的工艺单元的具体内容也很难保证一致;因此相似产品的工艺过程的工艺单元通常不存在完全等价的对应关系。工艺单元之间的差异性可由工艺单元节点的相似度来度量,对工艺单元节点进行匹配,基于匹配结果可得到整个工艺过程关于工艺单元的相似度。

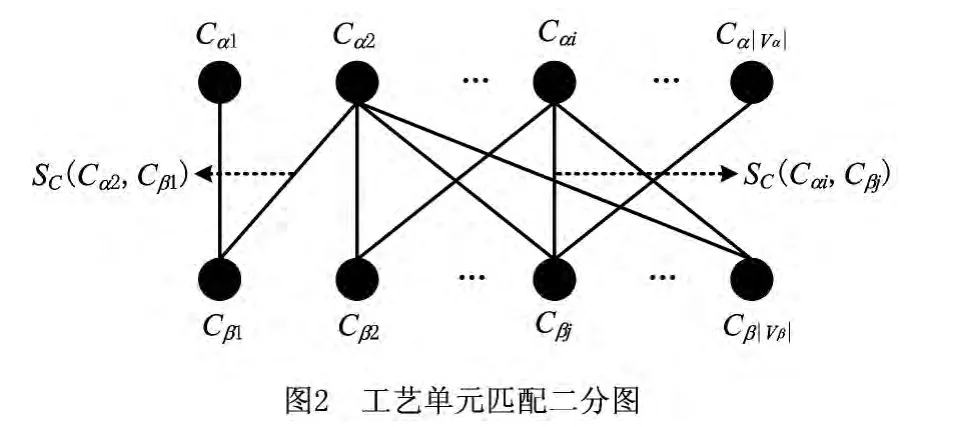
Kuhn-Munkres算法是加权二分图最优匹配问题常用的求解算法,该算法基于可行顶标的概念,通过不断修改顶标搜寻二分图相等子图的完备匹配。Kuhn-Munkres算法的具体步骤不在此赘述,若通过Kuhn-Munkres算法得到二分图Gαβ的最优匹配为M,则可获得工艺单元相似度SN(Gα,Gβ),

前文中提到工艺单元节点可用特征向量进行描述,因此工艺单元节点的相似度可用其特征向量间的相似度进行度量,本文采用余弦相似度来度量。有两个工艺单元节点的特征向量pi=(pi1,pi2,…,piL)和pj=(pj1,pj2,…,pjL),则这两个节点的相似度可用两向量间夹角的余弦表示,即工艺单元节点的相似度

1.2.2 工艺路线相似性
工艺过程的工艺路线相似性可通过图的邻接矩阵体现。工艺过程Gα的邻接矩阵可表示为Eα,其中元素的大小作为工艺单元节点Cαi到Cαj的有向边的权重,表示工艺单元Cαj对Cαi的依赖程度∈[0,1]。当=0时,表示两工艺单元节点间无关联关系;当=1时,表示工艺单元Cαj完全依赖于工艺单元Cαi。当对两个工艺过程Gα和Gβ进行比较时,由于工艺过程中的工艺单元节点不对等,需要对相应的邻接矩阵进行规范。假设Gα和Gβ分别为如图1所示的两个工艺过程v1→v2→v3→v4→v5→v7和v1→v2→v6→v5→v7,分别对其邻接矩阵进行规范化,得到规范化结构矩阵NEα和NEβ,如图3所示。
由工艺过程Gα和Gβ的规范化结构矩阵得到结构比较矩阵DEαβ,矩阵中的元素


由此可得工艺过程Gα和Gβ的结构比较矩阵,如图4所示。

由工艺过程Gα和Gβ的结构比较矩阵,可以得到工艺过程Gα和Gβ的工艺路线结构相似度

式中:N为规范化结构矩阵的列数;若≠1,则xij=1,否则xij=0。
2 典型工艺过程聚类
设有工艺过程集合GS,其大小为N,通过前文方法可以得到工艺过程集合GS中任意两工艺过程Gi和Gj的相似度S(Gi,Gj),其中i,j∈{1,2,…,N}。工艺过程集合的两两相似度可以构成其相似度矩阵SIMG=[S(Gi,Gj)]N×N。基于该相似矩阵对工艺过程集合进行聚类分析,进而可挖掘典型工艺过程。工艺过程的聚类具有聚类数量未知的特点,近邻传播(Affinity Propagation,AP)聚类算法[13]无需指定聚类数目及初始聚类的中心点,而且该算法运算速度快、稳定性好、聚类精度高,满足工艺过程聚类的实际需求。因此,本文基于近邻传播聚类,结合工艺过程聚类的有效性评价,建立典型工艺过程挖掘的半监督聚类算法。
2.1 工艺过程聚类的有效性及评价
设工艺过程集合GS被聚为K类,Ck表示第k个聚类,1<k≤K,gk表示Ck的聚类中心。gk作为聚类中心,与聚类Ck中其他工艺过程最为相似,聚类Ck中的其他工艺过程可以通过对聚类中心gk进行少许修改而获得。因此,工艺过程的聚类中心具有典型性,可作为典型工艺过程。在聚类Ck中,满足simG(gi,gk)<αk,其中gi∈Ck,1≤i≤|Ck|,则称该聚类的工艺过程集合为聚类中心gk的邻域,αk为邻域半径。某聚类为一个有效的聚类,需满足以下条件:①聚类Ck中工艺过程的数量应满足具体要求,即|Ck|≥η,η为聚类中最少的工艺过程数量,若|Ck|<η,则可认定该聚类不具备足够的参考价值;②聚类中心gk与聚类Ck中其他工艺过程之间的相似度应满足特定的约束,即当聚类中心gk的邻域半径αk小于规定值时,该聚类中心作为典型工艺过程才具有意义。
在聚类完成后,需对工艺过程聚类结果的优劣进行评价。Silhouette指标作为众多评价指标之一,由于其性能好、简单易用,故将其作为工艺过程聚类的评价指标。Silhouette指标体现了聚类内部的紧密程度和聚类之间的稀疏程度。对于任意有效工艺过程聚类Ci中的任一工艺过程实例gi,其Silhouette指标为

式中:a(i)为工艺过程实例gi与工艺过程聚类Ci中其他工艺过程实例的平均距离,
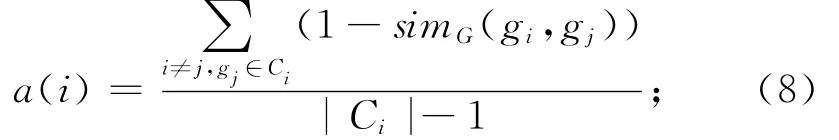
b(i)为工艺过程实例gi与其他有效工艺过程聚类的距离,
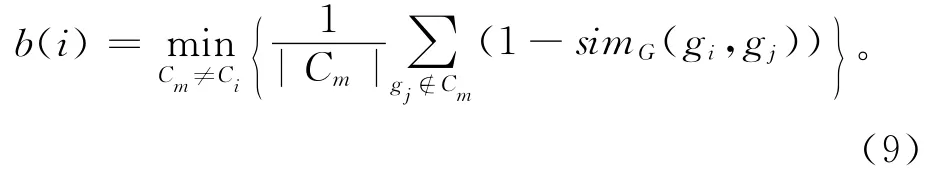
单个工艺过程聚类中所有工艺过程实例的Sil平均值包含了该类的紧密性,而整个工艺过程数据集的所有工艺过程实例的Sil平均值则反映了聚类结果的质量,Silhouette指标越大表示聚类质量越好。
2.2 基于近邻传播聚类的典型工艺过程发现算法
近邻传播聚类算法是在由聚类样本之间的相似度形成的相似矩阵SIM的基础上进行聚类的,而矩阵元素的取值一般为距离的负值。对于工艺过程聚类,AP算法将所有工艺过程样本作为可能的聚类中心,并通过样本间不断地进行信息传递形成最终聚类。在工艺过程样本之间存在可信度r(i,j)和可用度a(i,j)两种信息量参数。其中:r(i,j)是指相对于其他工艺过程,gj适合作为gi的典型工艺过程的程度;a(i,j)是指相对于其他工艺过程,gi选择gj作为其典型工艺过程的合适程度。AP算法的核心过程就是两个信息量交替更新的过程,如式(10)~式(12)所示:

式中sim(gi,gj)为相似矩阵SIM的矩阵元素,一般取sim(gi,gj)=-(1-simG(gi,gj)),i≠j。
鉴于前文对工艺过程聚类有效性的阐述,将AP算法用于工艺过程的聚类时需做以下工作:
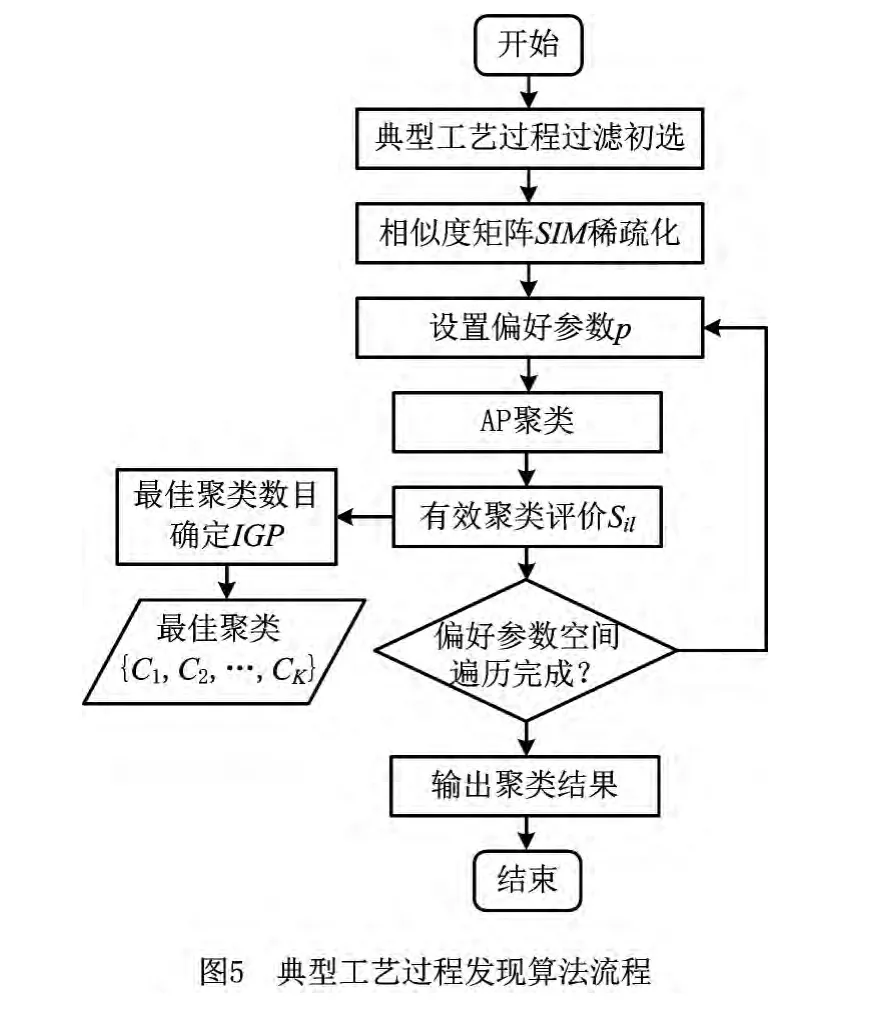
(1)典型工艺过程的过滤初选 由于AP算法将所有工艺过程样本都视为潜在的聚类中心,在考虑工艺过程聚类的有效性时,可以对工艺过程数据样本进行必要的过滤筛选。根据有效聚类的条件,对于给定的工艺过程样本gi,若|N(gi,ε)|<η,则gi不能作为有效聚类的中心,因此可在AP算法初始化时将其对应的偏好参数设置为最小值;若|N(gi,ε)|=0,则gi为游离的工艺过程,可从工艺过程的数据集中直接删除以减少算法的复杂度。
(2)相似度矩阵的稀疏化 由有效聚类的条件可知,聚类中心的邻域半径允许取的最大值为ε,而AP算法迭代过程中可信度与可用度的信息传递只需在相似度小于ε的工艺过程样本之间产生。因此,对相似度矩阵SIM的所有元素进行遍历,将相似度大于ε的元素设置为最小值,从而将相似度矩阵稀疏化。
(3)最佳聚类数的确定 在AP算法中,偏好参数p影响着最终聚类的数目,由于p的取值暂无确定的方法,在给定取值的情况下所得的聚类结果不能确保为最优结果。本文参照文献[14]给出的确定偏好参数取值区间[pmin,pmax]的方法,通过调节步长pstep遍历取值空间,首先通过Silhouette指标来评价聚类的有效性,而后采用IGP指标[15]对有效的聚类结果进行评价,以获得最佳聚类数目。IGP指标是基于概率统计思想提出的有效性评价指标,用来衡量在某一聚类中距离每个样本最近的样本是否在同一聚类中。对于类标为k的聚类,IGP指标定义为

式中:jN为距离样本j最近的样本;Class(j)为样本j的类标;#为满足条件的个数。
所有有效聚类的IGP指标越大,表示聚类的质量越好,其最大值对应的聚类数即为最佳聚类数。
基于以上工作,可以得到基于AP算法的工艺过程半监督最优聚类算法流程,如图5所示。
3 实例验证
下面以卫星结构板的制造工艺为研究对象,验证典型工艺过程发现算法的有效性。卫星结构板是各型号卫星上都大量采用的一类典型件,由于其功能、结构基本相似,研制流程基本一致,涵盖了面板机加、蜂窝芯材机加、嵌入件机加、嵌入件装配胶接等工艺过程。本文以面板机加工艺为例,从某卫星研制单位的结构板的历史工艺中取100个面板机加工艺过程实例,由于所取得的工艺过程实例的原始表达不能完全满足建立属性有向图模型的条件,根据1.1节中的描述,对工艺过程实例的表达进行再组织,建立了以备料、钣、铣轮廓、钻孔、镗孔、料_检、钣_检、数_检和入库等为工艺单元为基础的工艺过程实例库,对该工艺过程实例库进行聚类分析并发现面板机加的典型工艺过程。由结构板面板材料、制造特征及其关键参数等因素,可以确定面板的机加工艺分为5种类型,包括一般金属面板机加两类、加强金属面板机加两类和复合材料面板机加一类。所取的100个面板机加工艺过程实例包含这5种类型的工艺过程,其中包含了10个特殊面板机加工艺作为干扰样本。
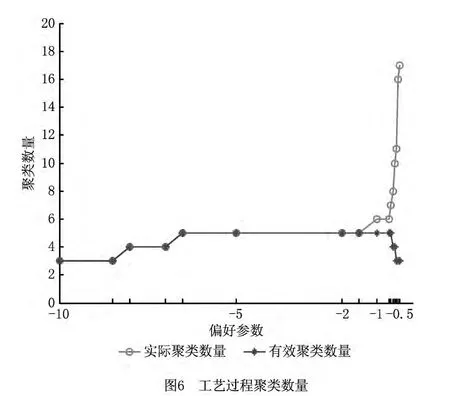
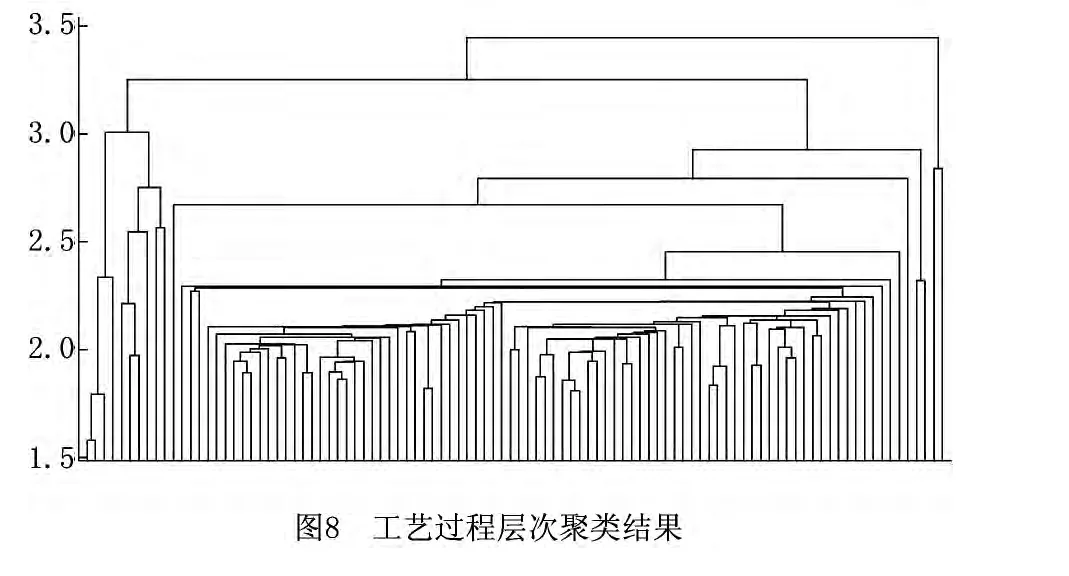
卫星结构板机加工艺过程聚类设置其有效聚类中所包含的最少工艺过程实例数为15,最大邻域半径为0.5,偏好参数调节步长为0.05。采用上文的聚类算法对卫星结构板机加工艺过程实例进行聚类。当偏好参数p=-0.65时,聚类评价指标Sil取得最大值3.349 6,此时,聚类数目为6和有效聚类数目为5,同时有效聚类数目为5时,其IGP指标取得最大值4.721 9,如图6和图7所示。参照文献[16]中偏好参数的选取方法,由两图中曲线的变化趋势可知,p较小时,聚类中所包含的工艺过程实例数量较多,有效聚类数量与实际聚类数量相近,聚类质量较高,且Sil与IGP指标变化趋势一致。此外,数据挖掘中常用的聚类方法还包括k-means方法、层次聚类方法等,其中,k-means方法对初始聚类中心的选择较为敏感,且聚类之前需指定目标聚类数目,不适用于典型工艺过程的聚类;层次聚类虽然无需事先确定聚类数目,但根据聚类层次树来确定最终的聚类结果仍存在困难,在此以所选取的工艺过程实例之间的相似度作为层次聚类中样本之间的距离,对工艺过程实例进行层次聚类,结果如图8所示,从图中的聚类层次树很难确定聚类结果。因此,相对于层次聚类,采用AP算法可以实现工艺过程的聚类。
4 结束语

本文针对工艺过程历史数据重用率低的问题,采用AP算法对历史工艺过程数据进行聚类分析,从而获取典型工艺过程。首先利用属性有向图对工艺过程进行描述,便于计算工艺过程实例间的相似度;将工艺过程的相似度矩阵作为AP聚类算法的输入进行聚类分析,并以Sil和IGP作为聚类结果的评价指标,以确定有效聚类及其最佳聚类数目。通过卫星结构板机加工艺的实例仿真验证了算法的有效性。在进行实例验证的过程中,虽然样本数量小、工艺过程实例的复杂度低,但工艺过程实例相似度的计算相对繁杂,因此降低工艺过程相似度计算的复杂性是后续的研究问题之一。
[1] LIU S,ZHANG Z,TIAN X.A typical process route discovery method based on clustering analysis[J].The International Journal of Advanced Manufacturing Technology,2007,35(1/2):186-194.
[2] ZHANG Hui,QIU Lemiao,ZHANG Shuyou,et al.Typical product process route extraction method on intelligent clustering analysis[J].Computer Integrated Manufacturing Systems,2013,19(3):490-498(in Chinese).[张 辉,裘乐淼,张树有,等.基于智能聚类分析的产品典型工艺路线提取方法[J].计算机集成制造系统,2013,19(3):490-498.]
[3] LONG Hongneng,YIN Guofu,CHENG Erjing,et al.Algorithm of process similarity analysis from case-based reasoning[J].Journal of Sichuan University:Engineer Science Edition,2004,36(1):77-82(in Chinese).[龙红能,殷国富,成尔京,等.基于实例推理的相似工艺度量算法[J].四川大学学报:工程科学版,2004,36(1):77-82.]
[4] THIMM G,JIANG F,BENG T S,et al.A graph representation scheme for process planning of machined parts[J].The International Journal of Advanced Manufacturing Technology,2002,20(6):429-438.
[5] DEMOLY F,YAN X T,EYNARD B,et al.An assembly oriented design framework for product structure engineering and assembly sequence planning[J].Robotics and Computer-Integrated Manufacturing,2011,27(1):33-46.
[6] ZHANG Zhiying,LI Zhen,JIANG Zhibin.Computer-aided block assembly process planning in shipbuilding based on rulereasoning[J].Chinese Journal of Mechanical Engineering,2008,21(2):99-103.
[7] BERGER U,KRETZSCHMANN R,NOACK J.An Approach for a Knowledge-based NC programming system[EB/OL].[2014-02-13].http://www-docs.tu-cottbus.de/automatisierungstechnik/public/2008_Kretzschmann_Madeira.pdf.
[8] ZHAO Gang,JIANG Pingyu.Weighted directed graph based part clustering model[J].Computer Integrated Manufacturing Systems,2006,12(7):1007-1012(in Chinese).[赵 刚,江平宇.基于加权有向图的零件聚类模型研究[J].计算机集成制造系统,2006,12(7):1007-1012.]
[9] SCHAEFFER S E.Graph clustering[J].Computer Science Review,2007,1(1):27-64.
[10] ZHOU Y,CHENG H,YU J X.Graph clustering based on structural/attribute similarities[J].Proceedings of the VLDB Endowment,2009,2(1):718-729.
[11] CHENG H,ZHOU Y,YU J X.Clustering large attributed graphs:a balance between structural and attribute similarities[J].ACM Transactions on Knowledge Discovery from Data,2011,5(2):1-33.
[12] XU Zhiqiang,KE Yiping,WANG Yi,et al.A model-based approach to attributed graph clustering[C]//Proceedings of the 2012ACM SIGMOD International Conference on Management of Data.New York,N.Y.,USA:ACM,2012:505-516.
[13] WANG Xianhui,QIN Zheng,ZHANG Xuanping,et al.Cluster ensemble algorithm using affinity propagation[J].Journal of Xi'an Jiaotong University,2011,45(8):1-6(in Chinese).[王羡慧,覃 征,张选平,等.采用仿射传播的聚类集成算法[J].西安交通大学学报,2011,45(8):1-6.]
[14] FREY B J,DUECK D.Clustering by passing messages between data points[J].Science,2007,315(5814):972.
[15] KAPP A V,TIBSHIRANI R.Are clusters found in one dataset present in another dataset?[J].Biostatistics,2007,8(1):9-31.
[16] ZHANG Yongjian.Research on methods and applications of complex product design process optimization[D].Harbin:Harbin Institute of Technology,2011(in Chinese).[张永健.复杂产品设计过程优化方法及其应用研究[D].哈尔滨:哈尔滨工业大学,2011.]
