考虑多失效模式的复杂系统运行可靠性评估
2015-07-25王华伟
高 军,王华伟
(1.军械工程学院 装备指挥与管理系,河北 石家庄 050003;2.南京航空航天大学 民航学院,江苏 南京 210016)
0 引言
运行可靠性是近年来可靠性工程领域重点关注的问题之一。复杂系统在运行过程中的可靠性往往动态变化,退化与突发失效共存,尤其是退化失效积累到一定程度后往往会引起突发失效的现象,从而显著增加了复杂系统的运行风险。在工程实践中,复杂系统往往通过加装状态监测系统,及时了解复杂系统的状态和可靠性,为在故障发生之前及时采取措施提供条件。因此,通过状态监测提取有价值的可靠性信息,是进行运行可靠性评估的关键。当前,针对复杂系统运行可靠性的研究,主要集中在利用在线监测数据、人工智能等方法进行可靠性预测方面。例如Chinnam[1]利用部件在线监测信息,结合系统结构构建通用复合模型,实现对复杂系统的在线监测;Li等[2]采用灰色模型预测在线可靠性,并通过在机械系统中的应用验证了模型的有效性;Lolas等[3]利用专家系统和神经网络方法,对不同阶段的信息进行实时更新,实现了对可靠性的预测;Bosnic等[4]采用不同的回归模型进行可靠性预测,得到组合模型有助于改进预测结果的结论。另外,还有学者从复杂系统结构特点的角度,进一步探讨了运行可靠性评估问题。例如:Li等[5]研究了多态关联系统运行可靠性评估问题;Lu等[6]利用卡尔曼滤波模型处理多源状态监测信息,研究了基于多失效模式的复杂系统可靠性动态评估;吴军等[7]综合应用Bootstrap和支持向量机等方法建立了小样本条件下的可靠性评估模型。
复杂系统运行阶段突发失效和退化失效的失效机理及对可靠性的影响各不相同,直接决定着运行可靠性评估的准确度和可信性。Xiao等[8]针对多故障模式系统,研究了故障模式与影响分析(Failure Model and Effect Analysis,FMEA)方法,并优化了风险系统的权重因子;Boutsikas等[9]针对一类多失效模式系统研究了可靠性分析方法;Pickard等[10]提出一种将多失效模式进行组合分析的方法;Yang等[11]针对复杂可修的多失效模式系统,采用极大似然方法进行了故障剖面分析;Zhang等[12]结合分层抽样和重要性抽样方法的优点,提出采用分层重要度分析多失效模式结构的方法;Milienos等[13]采用随机序方法建立了多失效模式系统的可靠性函数模型,计算了多故障模式系统可靠性置信下限;Wang等[14]针对多部件系统和多失效模式系统建立了基于延迟时间的检查模型;胡剑波等[15]分析了多失效模式竞争发生的情况,研究了多失效模式系统的退化变迁模型,并以此为基础制定了维修决策。综上所述,可以发现这些研究多是在设计阶段进行可靠性分析与评估,而从多失效模式的角度进行系统运行可靠性评估的文献还很少见。
本文结合当前复杂系统运行可靠性评估和多失效模式分析研究的相关成果,研究考虑了多失效模式的复杂系统运行可靠性评估方法。
1 复杂系统运行可靠性评估体系设计
退化失效和突发失效是复杂系统运行阶段的两大类失效模式,对复杂系统运行可靠性的影响有着各自的特点,主要体现在以下几个方面:
(1)从作用机理来看,性能退化失效主要是由摩擦、磨损等因素导致的,而突发失效可以由意外冲击、工作条件的突然变化引起,也可能是退化失效累积到一定程度后引起的系统状态突变,以突发失效的形式表现出来。
(2)从表现形式来看,退化失效往往表现出渐进性,可以通过加装监测系统实现对退化失效的监测,而突发失效则往往是在没有任何征兆的情况下突然发生的,具有小样本的特征。
(3)从定量分析的角度来看,退化失效贯穿于复杂系统运行的全过程,在各阶段主要体现为退化失效速率大小的变化,且退化失效不可逆,而突发失效在系统运行阶段可能发生也可能不发生,其失效率大多符合传统的可靠性分析中的浴盆曲线。
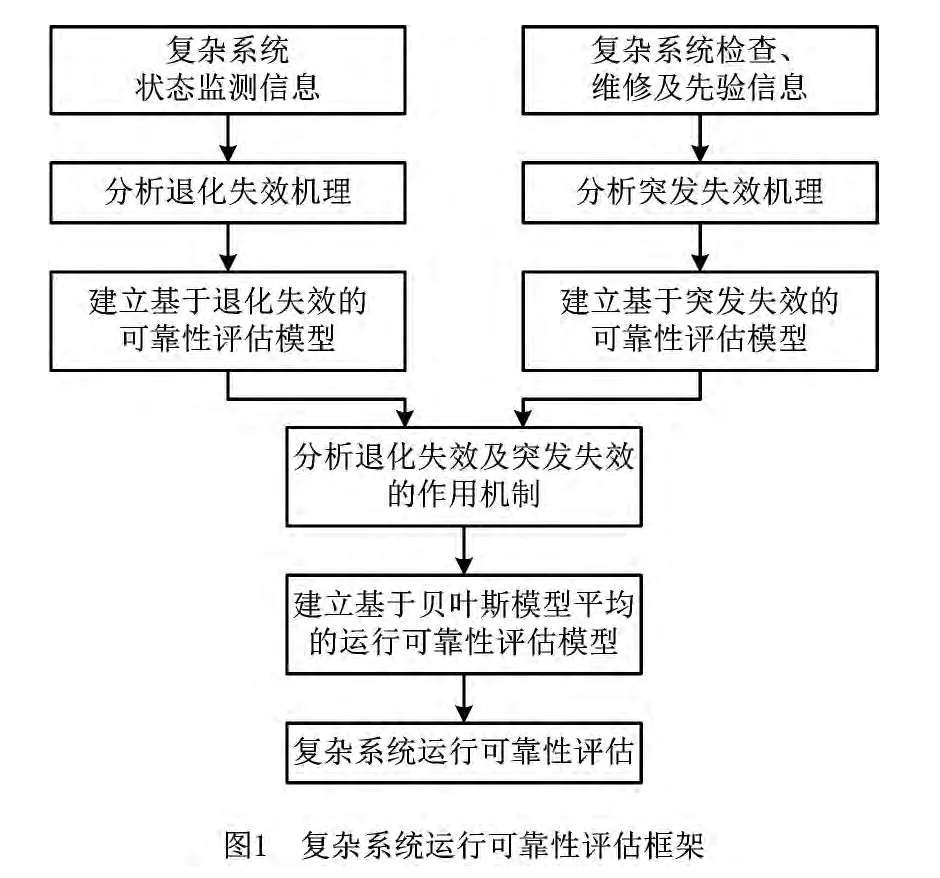
因此,复杂系统运行可靠性评估可以分解为3个问题:①对退化失效的可靠性评估,其关键是从状态监测中提取有价值的可靠性信息并用于退化评估;②对于突发失效评估,既要考虑失效本身形成的机理,还要兼顾退化失效积累到一定程度后以突发失效的形式表现的问题;③分析以上两种失效对运行可靠性的影响,采用竞争风险分析方法,以T=min{T退化,T失效}作为系统剩余寿命,分别测算复杂系统的退化失效可靠度和突发失效可靠度,并在假设两者串联的情况下计算系统的运行可靠性。但实际上,在系统运行的不同阶段,往往是退化失效和突发失效中的一种占主导地位,而不是两者同时起作用,故有必要分析两者对系统运行可靠性影响的权重,避免出现低估可靠性的现象。为此,本文构造了复杂系统运行可靠性的评估框架,如图1所示。
2 复杂系统运行可靠性评估模型
2.1 考虑退化失效的运行可靠性评估模型
针对复杂系统运行过程具有的失效渐进和不可逆等特点,选择Gamma分布建立退化失效的可靠性评估模型,可表示随使用时间增加而单调下降的变化特性,比其他随机过程更能满足运行过程中关于复杂系统运行退化失效的假设。在实际使用中,针对采集到的使用数据,应预先检验是否符合Gamma过程假设。假设t时刻复杂系统的性能退化量为d(t),失效阈值为l,即当D(t)≥l时,复杂系统发生退化失效。假设复杂系统的初始性能退化记为D0,则w(t)=D(t)-D(t0)表示到t时刻复杂系统累积的退化量。由于退化量单调上升,对于任意的ti和tj,如果tj>ti,则必有w(tj)-w(ti)>0。假设退化量w(t)服从Ga(a,b),其密度函数为
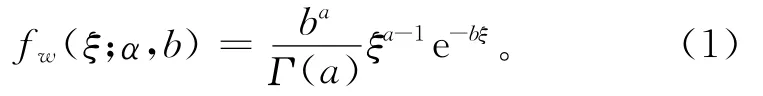
式中a和b分别为形状参数和尺度参数。
性能退化失效的可靠性
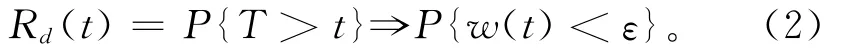
式中ε为复杂系统的性能失效阈值。
由式(1)和式(2),性能退化失效的复杂系统可靠度
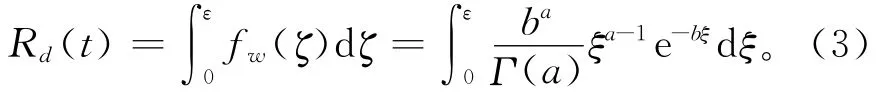
在系统退化可靠性评估中,估计性能退化量是计算的核心,综合利用多源状态监测信息将显著提高退化量的估计结果,本文采用贝叶斯线性模型[16]进行估计。
假设复杂系统的退化可以通过以下性能监测参数来表征:监测参数矩阵X=[X1,X2,…,Xk],其中:k为监测参数的个数,Xk为n行列向量,n为观测的次数。性能退化与状态监测参数之间的关系,可以用随机方程表示为


通过监测参数,可计算,均值为E(θ),协方差矩阵为C(θ)。
假设监测参数符合逆Gaussian分布,状态监测的参数量越多,描述系统退化的精度和准确度就越高。上述监测参数采用贝叶斯线性模型[16]进行融合计算,后验均值和协方差可表示为:
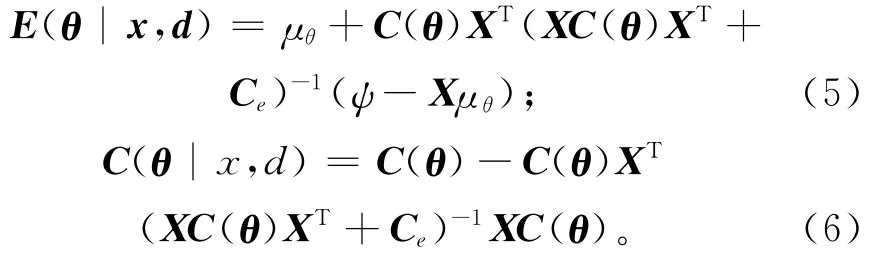
在给定观测集X后,通过θ先验期望计算后验期望,计算方法是使贝叶斯 MSE(mean square error)矩阵()最小,
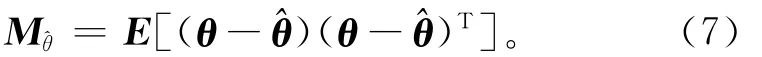
按照上述方式可得到线性最小均方差(Linear Minimum Mean Square Error,LMMSE)估计量。
2.2 考虑突发失效的复杂系统运行可靠性评估模型
Weibull分布是工程领域广泛使用的一种方法,可以通过对其参数的不同取值,近似接近其他分布形式,具有良好的适应性,本文采用Weibull建立的针对突发失效的复杂系统运行可靠性评估模型。本文针对复杂系统突发失效的假设,可体现突发失效自身的机理及由退化失效到一定程度后引发的突发失效表现形式,反映了退化失效对寿命变化规律的影响,因此在一定程度上可以描述出性能退化失效和突发失效之间的相互关系。
假设复杂系统突发失效的寿命变化规律符合Weibull分布,其概率密度函数表达式为
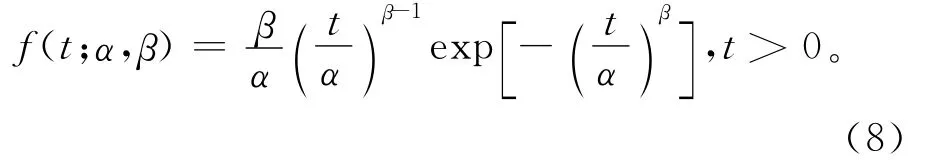
式中α>0,β>0分别表示尺度参数和形状参数。
形状参数一般反映退化失效对突发失效的影响,可以通过退化量w进行描述。在形状参数已知的情况下,系统突发失效的可靠性评估可以转化为对尺度参数α的计算。假设尺度参数具有共轭Gamma先验分布,即

式中c和d是尺度参数的共轭先验的超参数。通过采集尺度参数的先验均值和方差,可得到超参数c和d的取值,进一步可计算出尺度参数的后验均值和方差,实现突发失效的可靠性评估。
针对更加普遍的情况,通过数据学习可确定突发失效关于退化量的条件概率,用来分析退化失效对突发失效的影响。考虑到退化量的特征分布是时间函数,上述过程可以简化。通过基于退化量突发失效的条件概率和突发失效概率分布的联合分布函数计算可靠度,相关求解方法可用蒙特卡洛仿真实现。
突发失效可靠度

2.3 基于贝叶斯模型平均的复杂系统运行可靠性评估模型
贝叶斯模型平均(Bayesian Model Averaging,BMA)是一个结合多个统计模型进行联合推断和预测的统计后处理方法[17]。令f={f1,f2}表示复杂系统运行可靠性的评估模型,f1表示退化失效可靠性评估模型,用Gamma过程描述,f2表示突发失效可靠性评估模型,用 Weibull分布描述。传统的BMA模型是针对多个正态分布模型进行平均的,本文的两个可靠性评估模型分布形式不一致,考虑到Weibull分布本身具有很大的适应性,本文假设运行可靠性符合Weibull分布。系统运行可靠性评估的表达式为:

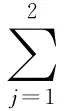
经贝叶斯模型平均后,后验的期望值和期望可以表示为:
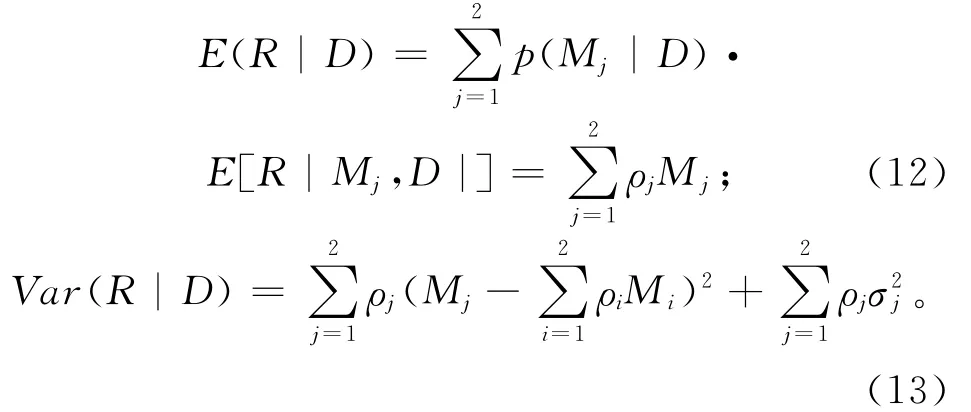
其中为模型Mj基于数据集D的预测方差。由式(14),BMA的预报方差包括两项:①评估集合内的离散程度;②预测模型本身的方差。
3 复杂系统运行可靠性评估算法
复杂系统运行可靠性评估的算法步骤如下:
(1)融合状态监测信息,评估退化水平
利用2.1节的贝叶斯线性模型,融合多种来源的状态监测信息,运用式(5)和式(6)计算状态监测参数与累计退化量函数关系的期望和方差值;建立多元状态监测信息与累计退化量的关系;在输入新的监测信息后,利用式(4)评估复杂系统的退化水平。
(2)计算复杂系统退化失效可靠度
利用预测的退化期望值,按照式(3),采用Monte-Carlo仿真方法计算复杂系统退化失效的可靠性。
(3)计算突发失效Weibull分布的尺度参数
假设复杂系统突发失效的尺度参数服从逆Gamma分布,其先验分布参数为Ga(γ,η),则需要进一步确定逆Ga(γ,η)的超参数,即通过首先确定先验参数,再进行参数的学习来计算。
假设在系统运行初期已知时刻的突发失效可靠度和方差,则尺度参数

已知参数α的均值和方差,则超参数a和b可以通过式(15)和式16)计算得到:

采集 突 发 失 效 观 测 数 据 {(t1,n1),…,(tm,nm)},其中ti表示突发失效的发生时间,ni表示突发失效样本数,经学习后的后验参数γ′和η′可表示为:
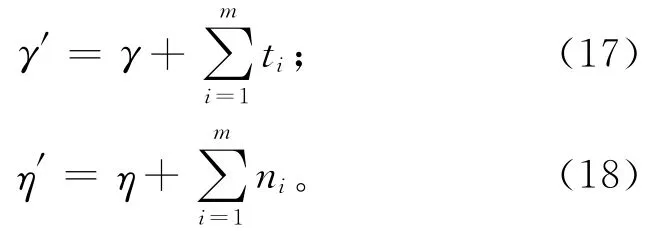
需要说明的是,如果在系统运行过程中采集到检查信息和维修信息,则应采用贝叶斯信息融合方法,修正先验信息并调整相关参数。
(4)计算突发失效可靠度
结合步骤(1)计算的退化期望值和步骤(3)计算的突发失效尺度参数,利用预测的退化期望值,应用式(10),采用马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)仿真方法计算复杂系统突发失效的可靠性。
(5)采用BMA方法计算运行可靠度

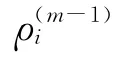
2)计算候选点θ*的接受概率

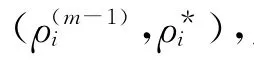
经过充分的迭代后,M-H算法使Markov链收敛于目标分布π(ρi)。
4 数值算例
为说明本文所提方法的应用过程,选择某型航空发动机作为研究对象。该研究对象满足前文对复杂系统运行可靠性评估的基本假设:①该发动机在运行过程中同时存在退化失效和突发失效;②该发动机的退化是不可逆转的,体现为若未经维修,则只能表现为可靠性逐渐降低;③该发动机具有完善的在线状态监测系统,便于提取和采集监测信息,跟踪性能退化过程;④航空发动机直接涉及到飞行安全,突发失效发生频率低。
采集某机队已经发生更换的35个发动机样本,监测如下6个参数:DEGT(涡轮后燃气温度偏差)、GWFM(燃油消耗量偏差)、GPCN25(高压转子转速偏差)、DPOIL(滑油压力)、ZVBIF(低压转子振动值偏差)和ZVB2R(高压转子振动值偏差),发动机在翼时间TSI(time since installation)的单位是飞行小时(Fight Hour,FH)。采集已经发生更换和拆卸的发动机机队信息,提取发生拆卸时的状态监测参数和在翼寿命,采用Gamma过程计算性能的退化程度,计算状态监测参数与性能退化之间的关系;跟踪某台发动机从开始投入使用到发生更换拆卸的寿命周期过程,获取9个监测点的信息和使用时间,根据航空发动机的实际在翼寿命,逆向计算各监测点的实际可靠度,并与模型计算结果进行对比。本算例的计算流程如图2所示。

35个经无量纲化的状态监测参数如图3所示,贝叶斯线性模型融合计算结果与性能退化程度的对比如图4所示。进一步,本文跟踪了某发动机在线监测的9个样本,分别对其进行性能退化可靠性评估和突发失效可靠性评估,相关参数及可靠性评估结果如表1所示。
由图4可见,融合的状态监测参数与实际的性能退化值有较好的拟合度,可以利用上述提取的关系跟踪在线监测样本。
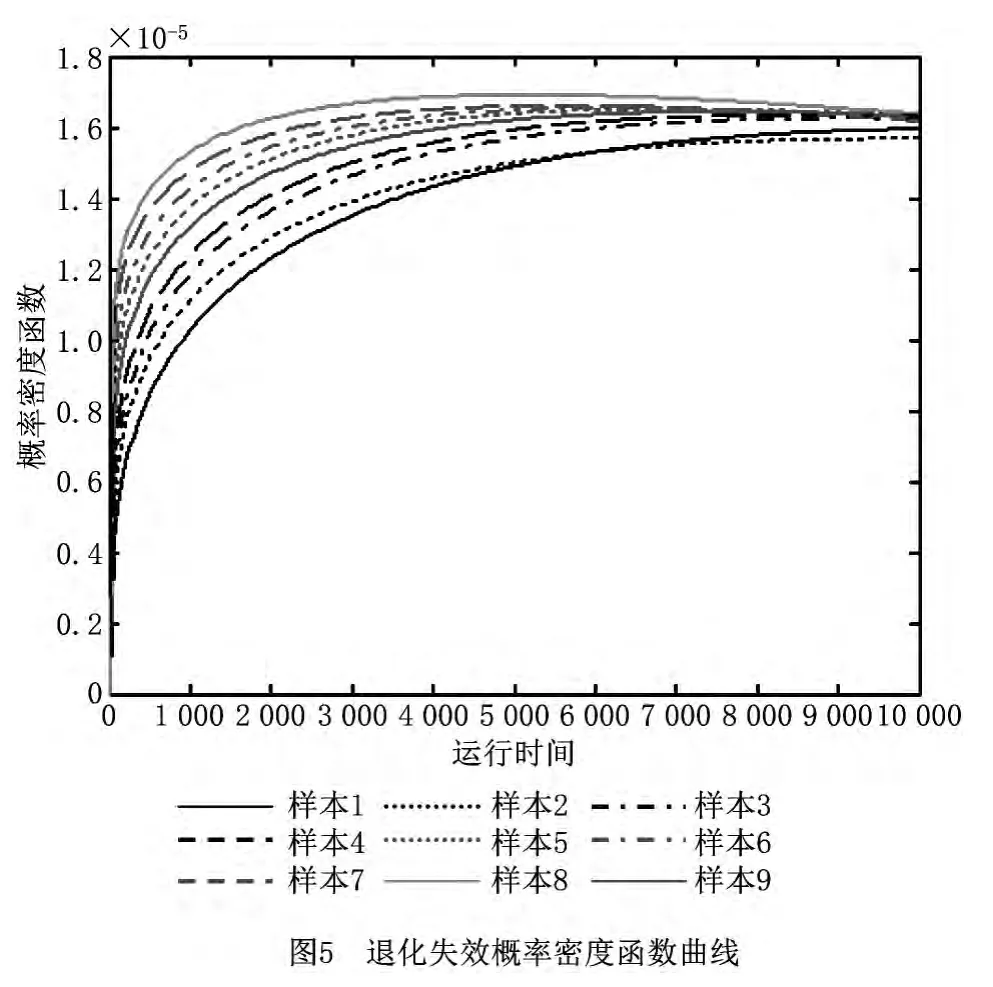
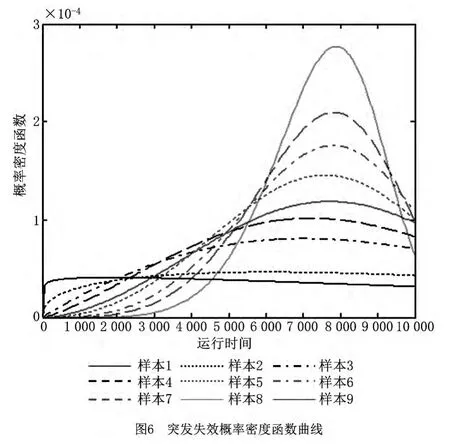
图5和图6分别表示突发失效与退化失效的概率密度函数曲线。可以看出,退化失效具有渐进性,而突发失效则具有较大的波动性,符合退化失效和突发失效的工程特点。
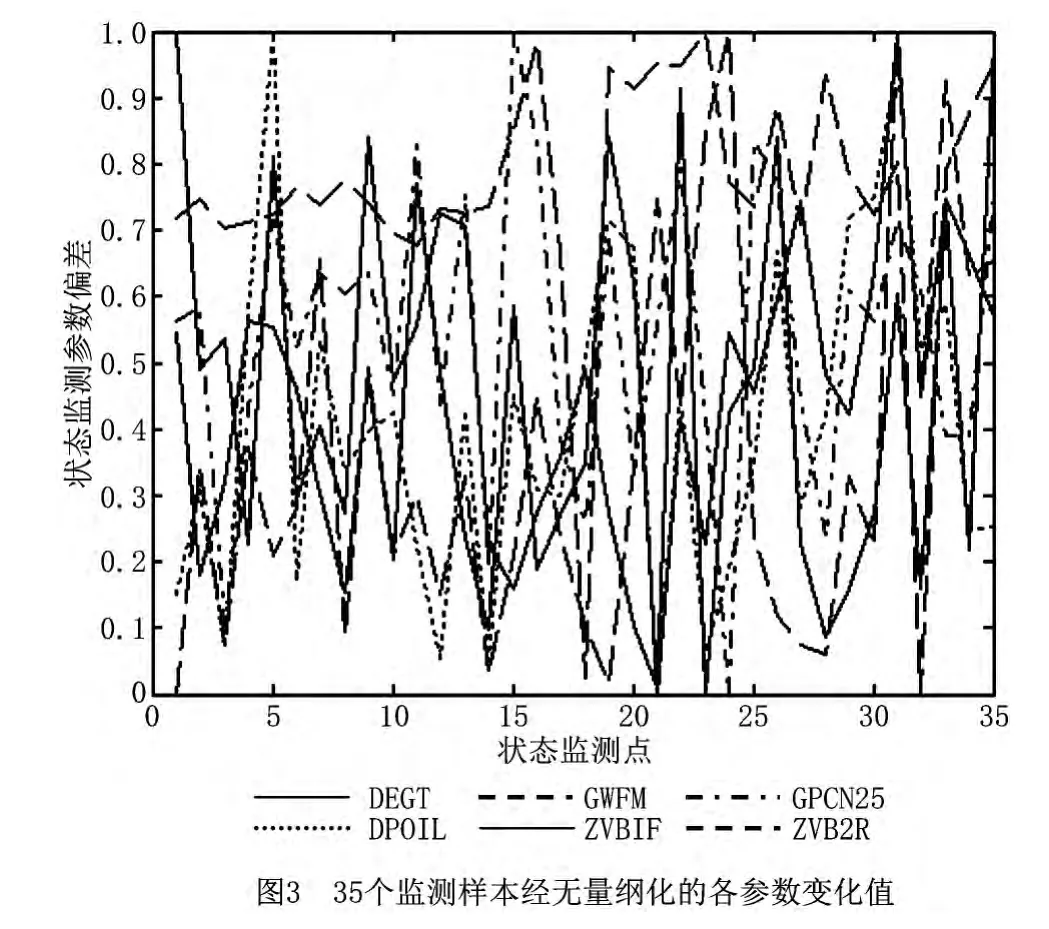


表1 某型航空发动机退化失效及突发失效可靠性评估
进一步结合已经采集到的该发动机在各拆卸时刻点的可靠度信息,采用BMA方法,对退化失效和突发失效模型进行训练,相关结果如表2所示。
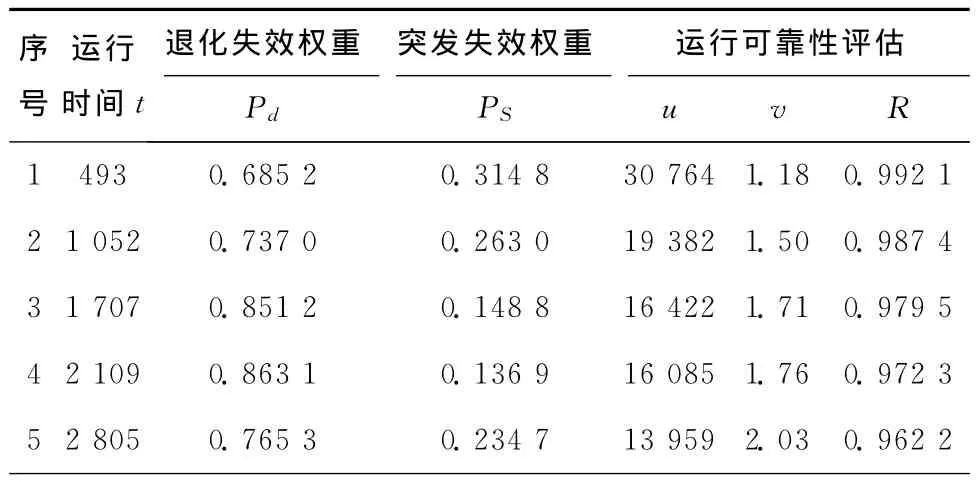
表2 某型航空发动机失效权重及运行可靠性评估
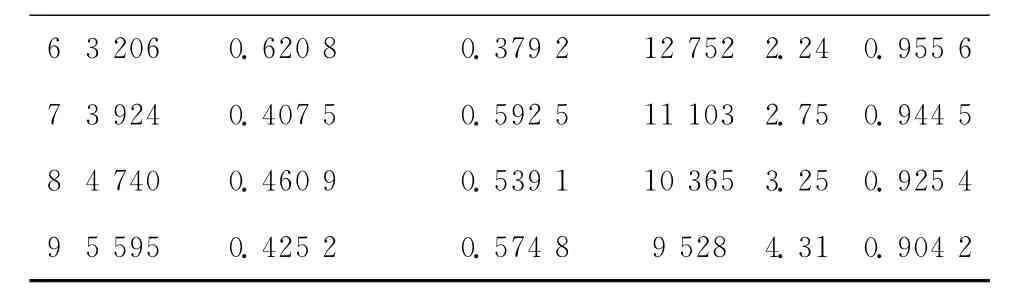
续表2
运行可靠性失效概率的密度曲线如图7所示,可靠度变化曲线如图8所示,退化失效和突发失效的权重概率密度函数曲线如图9和图10所示。由图7和图8可以看出,运行可靠性曲线较好地平均了退化失效和突发失效可靠性曲线,体现了复杂系统运行过程中的平稳性和可靠性降低的渐进性。


由图9和图10可以看出,退化失效的权重在对整个运行可靠性影响中占主导地位,尤其是在系统运行的前期,退化失效是复杂系统的主要失效模式;而在系统运行后期,突发失效的可能性将逐步提高。

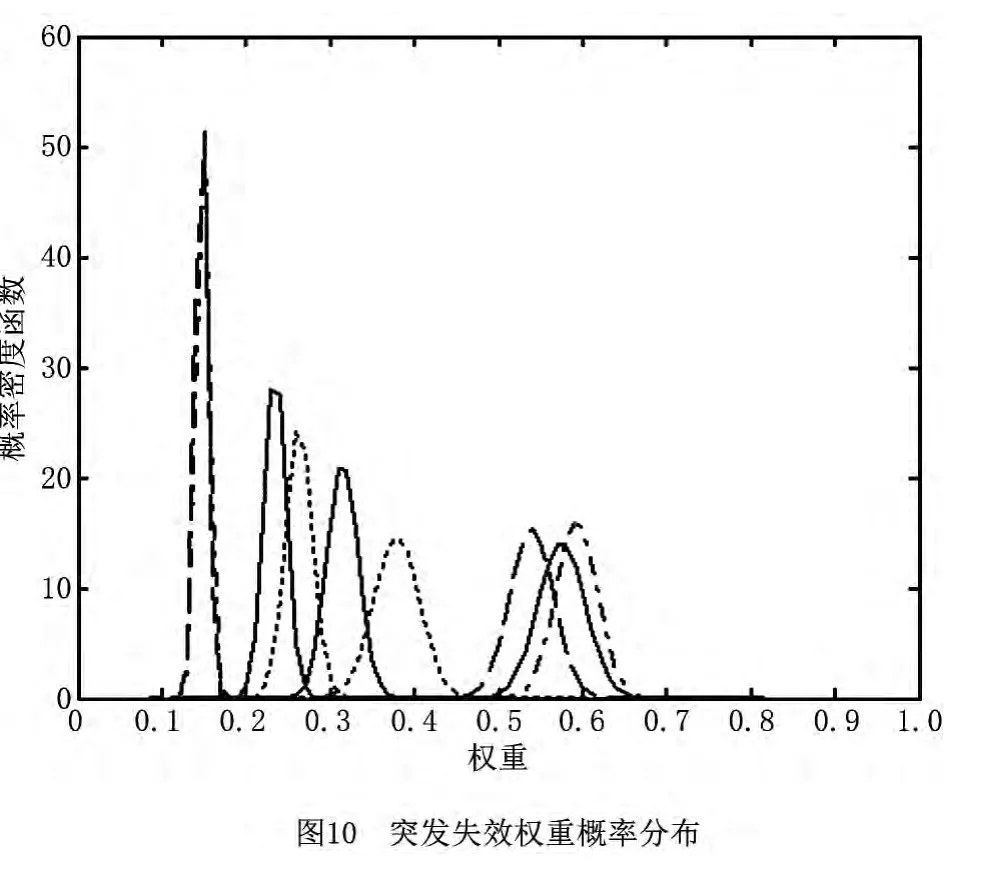
表3给出了退化失效可靠度、突发失效可靠度、运行可靠度与实际可靠度水平的对比值,其中实际可靠度根据该发动机实际在翼寿命逆向计算得到。由表3可知,运行可靠性评估值在总体上优于退化失效可靠性评估值和突发失效可靠性评估值。
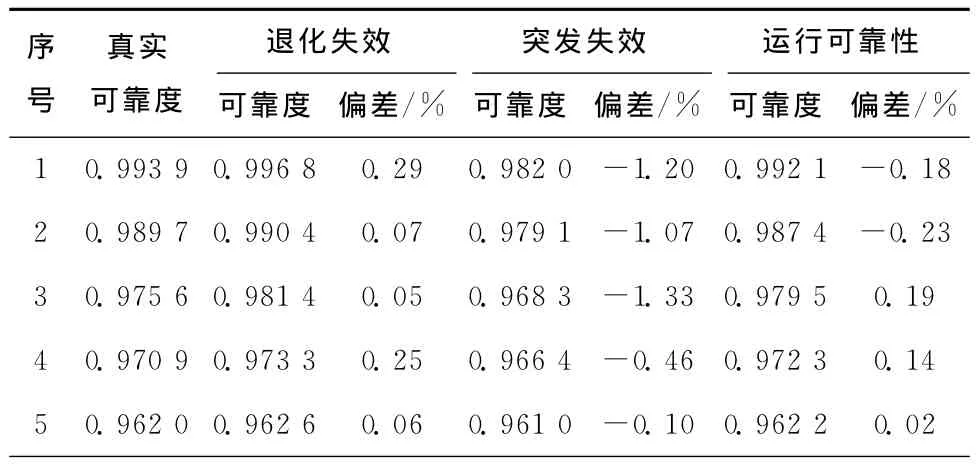
表3 某型航空发动机运行可靠性评估误差分析

续表3
5 结束语
本文针对复杂系统运行中退化失效和突发失效同时存在的实际,利用其运行过程采集的状态监测信息、专家信息、维修信息和检查信息,分别针对退化失效和突发失效建立相应的可靠性评估模型,利用贝叶斯模型平均技术,分析退化失效和突发失效对系统运行可靠性的影响,评估复杂系统运行的可靠性。采集了某型航空发动机的运行数据,说明了本文提出的方法对算例是有效的。本文将状态监测的研究成果与基于贝叶斯的小样本可靠性评估成果有机结合起来,通过状态监测数据提取有价值的可靠性信息,进一步通过数据分析不同失效对运行可靠性的影响,目标是通过模型描述复杂系统运行阶段失效的转换与切换,提高运行可靠性评估的准确度。今后在有足够数据支撑的条件下,对退化失效和突发失效还可以进一步细化,分析影响复杂系统运行可靠性的关键因素和重要失效模式,为提高运行可靠性水平提供有力支持。
[1] CHINNAM R B.On-line reliability estimation for individual components using statistical degradation signal models[J].Quality and Reliability Engineering International,2002,18(1):53-73.
[2] LI G D,MASUDA S.A new reliability prediction model in manufacturing systems[J].IEEE Transactions on Reliability,2010,59(1):170-177.
[3] LOLAS S,OLATUNBOSUN O A.Prediction of vehicle reliability performance using artificial neural networks[J].Expert Systems with Applications,2008,34(4):2360-2369.
[4] BOSNIC Z,KONONENKO I.Comparison of approaches for estimating reliability of individual regression predictions[J].Data & Knowledge Engineering,2008,67(3):504-516.
[5] LI J A,WU Y,LAI K K,et al.Reliability estimation and prediction of multi-state components and coherent systems[J].Reliability Engineering & System Safety,2005,88(1):93-98.
[6] LU H T,KOLARIK W J,LU S S.Real time performance reliability prediction[J].IEEE Transactions on Reliability,2001,50(4):353-357.
[7] WU Jun,DENG Chao,XIONG Qiangqiang,et al.Reliability assessment method based on bootstrap and SVM[J].Computer Integrated Manufacturing Systems,2013,19(5):1058-1063(in Chinese).[吴 军,邓 超,熊强强,等.基于 Bootstrap与SVM集成的可靠性评估方法[J].计算机集成制造系统,2013,19(5):1058-1063.]
[8] XIAO N C,HUANG H Z,LI Y F,et al.Multiple failure mode analysis and weighted risk priority number evaluation in FMEA [J].Engineering Failure Analysis,2011,18(4):1162-1170.
[9] BOUTSIKAS M V,KOUTRAS M V.On a class of multiple failure mode systems[J].Naval Research Logistics,2002,49(2):167-185.
[10] PICKARD K,MüLLER P,BERTSCHE B.Multiple failure mode and effects analysis:an approach to risk assessment of multiple failures with FMEA[C]//Proceedings of Reliability and Maintainability Symposium.Washington,D.C.,USA:IEEE,2005:457-462.
[11] YANG Q Y,HONG Y L,CHEN Y,et al.Failure profile analysis of complex repairable systems with multiple failure modes[J].IEEE Transactions on Reliability,2012,61(1):180-191.
[12] ZHANG F,LU Z Z,CUI L J.Reliability sensitivity algorithm based on stratified importance sampling method for multiple failure modes systems[J].Chinese Journal of Aeronautics,2010,23(6):660-669.
[13] MILIENOS F S,KOUTRAS M V.A lower bound for the reliability function of multiple failure mode systems[J].Statistics & Probability Letters,2008,78(12):1639-1648.
[14] WANG W B,BANJEVIC D,PECHT M.A multi-component and multi-failure mode inspection model based on the delay time concept[J].Reliability Engineering &System Safety,2010,95(8):912-920.
[15] HU Jianbo,GE Xiaokai,ZHANG Liang,et al.Degradation shift modeling and condition maintenance descsion optimization of multi-failure system[J].Computer Integrated Manufacturing Systems,2014,20(1):165-172(in Chinese).[胡剑波,葛小凯,张 亮,等.多失效系统退化变迁建模与状态维修决策 优 化 [J].计 算 机 集 成 制 造 系 统,2014,20(1):165-172.]
[16] GOLDSTEIN M,WOOFF D.Bayes Linear statistics,theory& methods[M].New York,N.Y.,USA:John Wiley &Sons,2007.
[17] RAFTERY A E,GNEITING T,BALABDAOUI F,et al.Using Bayesian model averaging to calibrate forecast ensembles[J]. Monthly Weather Review,2005,133 (5):1155-1174.
