基于并行模拟退火算法求解时间依赖型车辆路径问题

穆 东，王 超，王胜春，周圣川

（1.北京交通大学 经济管理学院，北京 100044；2.北京工业大学 经济与管理学院，北京 100124；3.北京交通大学 计算机与信息技术学院，北京 100044；4.青岛市勘察测绘研究院，山东 青岛 266032）

1 问题的提出

1.1 时间依赖型车辆路径问题

1959年Dantzig等［1］首次提出车辆路径问题（Vehicle Routing Problem，VRP）模型，随后许多学者研究了带时间窗的车辆路径问题（Vehicle Routing Problem with Time Windows，VRPTW），即在VRP问题上加上了顾客被访问的时间窗限制。但VRPTW的研究大多基于静态路网的假设，即车辆行驶速度恒定、车辆在路段上的运行时间是静态的。但在实际路网中，由于受上下班高峰期、天气变化和突发事故等因素的影响，车辆出发时间、路段的行驶速度和行驶时间总是处于不断变化中。1981年，Beasley［2］提出时间依赖型车辆路径问题（Time Dependent Vehide Routing Problem，TDVRP），研究路径行驶时间随出发时间变化的路网环境下，如何安排车辆配送路线，以达到一定的优化目标（如路径最短、费用最少、时间最少、使用车辆最少等）。随着现代物流的发展，城市交通负载日益繁重，传统的VRP模型难以满足快捷、高效配送的要求，因此，研究TDVRP十分必要。VRPTW已被证明是NP-hard问题［3］，而TDVRP比 VRPTW 更复杂，求解也更加困难。

从已有文献可以看出，相对于对VRP和VRPTW的研究，对TDVRP的研究要少许多［4］。Malandrak等［5］给出了TDVRP的混合整数规划模型，并设计了最近邻法和割平面启发式算法，可以求解10～25个客户规模的TDVRP。随后，Park等［6］构造了节约算法、近似最优搜寻技术和插入算法，Park［7］构造了双层节约算法，Bill等［8］构造了吝啬算法求解TDVRP。但是早期TDVRP的研究忽略了路网中应满足“先进先出”（First in First out，FIFO）准则。Ichoua等［9］将 FIFO 准则引入 TDVRP，采用速度时间依赖函数表示动态路网。FIFO准则保证了车辆k1在t时刻从顾客i驶向顾客j，另一同类型的车量k2在t＋η（η＞0）时刻也从顾客i驶向顾客j，则车辆k2总是比车辆k1后到达。随后，Van Woensel等［10］使用禁忌搜索算法，求解32～80个顾客规模的TDVRP；Donati等设计了单蚁群系统［11］和多蚁群系统［12］优化算法求解100个顾客规模的TDVRP；王正国等［13］构建了适应性禁忌搜索算法，求解带回程的TDVRP；李妍峰［14］引入了大规模邻域搜索技术和环状交换算法求解TD-VRP；段征宇等［15］使用“最大—最小蚂蚁系统”改进蚁群系统求解TDVRP；Kuo等［16］设计了串行模拟退火算法，寻找碳排放量最少的路径。然而，目前已经发表的文献由于节点规模、目标函数和约束条件的不同，不能进行解的质量和计算时间的对比。在此背景下，Figliozzi［4］改进了Solomon测试数据库，设计了Figliozzi测试数据库，用于对求解TDVRP的不同算法进行对比。为此，本文满足FIFO准则，提出TDVRP的并行模拟退火（paralle-Simulated Annealing，p-SA）算法，并使用Figliozzi数据库对该算法的性能进行测试，以确定其有效性。

1.2 动态路网的表示

目前，对时间依赖函数的研究，主要停留在比较理想的状态，即忽略大量的随机因素，主要考虑人们的出行规律和管制，这些因素使行驶时间呈周期性变化。目前的时间依赖函数可分为以下两类：

（1）Malandraki模型［5］该模型将每天的时间分成N个小段，每小段内的行驶时间固定，为阶梯函数，如图1所示。在图中，1-2这段时间间隔内的行驶时间是0-1这段时间间隔的行驶时间的2倍。目前，多数对TDVRP的研究都是使用这种时间依赖函数。但Malandraki模型的最大缺陷是不满足FIFO准则。

（2）Ichoua模型［9］该模型用行驶速度代替行驶时间，通过路径长度和行驶速度计算行驶时间，从而使行驶时间连续变化，该方法可以满足FIFO准则，但其行驶速度存在跃迁变化，与实际情况差异较大。图2中将行驶速度表示为分段函数的形式（如图2a），由此得到连续的行驶时间函数（如图2b），使得路网满足FIFO特性。

本文认为，在实际情况中，车辆行驶速度的变化不是阶跃变化，而是平滑改变。如果车辆的行驶在一天内，则应该考虑运输路线早高峰、晚高峰路线的行驶速度依赖函数，如图3所示。理论上讲，只要速度函数是连续变化的，车辆的运行时间就能够计算（采用积分方法），从而可以整体反映实际路况中车速的变化，该模型也满足FIFO准则。

1.3 TDVRP问题的描述及数学模型

本文研究的是硬时间窗TDVRP，即不能违反顾客的时间窗要求。TDVRP可描述为一个无向连通图G＝（V0，E），其中，V＝｛1，2，…，n｝为顾客的集合，0表示中心仓库（depot），V0＝V∪｛0｝，E为边的集合且E＝｛〈i，j〉｜i，j∈V0，i≠j｝。中心仓库拥有m辆汽车（K＝｛1，2，…，m｝），容量分别为Qk（k∈K）。每位顾客的需求量为qi（i∈V），完成顾客i的任务需要的时间（服务时间）为TSi，且顾客i必须在时间窗［ETi，LTi］内完成，其中ETi为任务i的最早允许开始时间，LTi为任务i的最迟允许开始时间。如果车辆到达顾客i的时间早于ETi，则车辆需要在i处等待，等待时间为WTi，车辆到达时间不能晚于LTi。一车辆到达一个顾客i（i∈V）的时间为ATi，离开时间为DTi。要求合理安排配送路径，使得目标函数最小，并满足：①每个客户的需求必须满足，且只能由一辆车送货一次；②每辆车只能服务一条路径，配送车辆都始发和终止于中心仓库；③满足车辆载货能力约束和时间窗的约束。

定义参数如下：yjk（j∈V，k∈K）表示顾客j被车辆k开始服务的时间；dij表示从点i到点j的欧式距离；vijk表示车辆k从点i到点j的速度；tijk（DTi）表示车辆k从点i到点j的行驶时间，是关于车辆k离开顾客i的时间DTi的函数；xijk为决策变量，如果车辆k从点i行驶到点j，则xijk＝1，否则xijk＝0。

参考 Desrochers［17］的 VRPTW 模型，可得 TDVRP问题的数学模型如下：

主目标函数：

次目标函数：

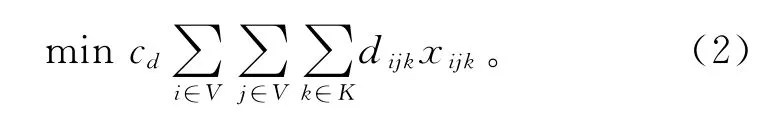
约束条件：

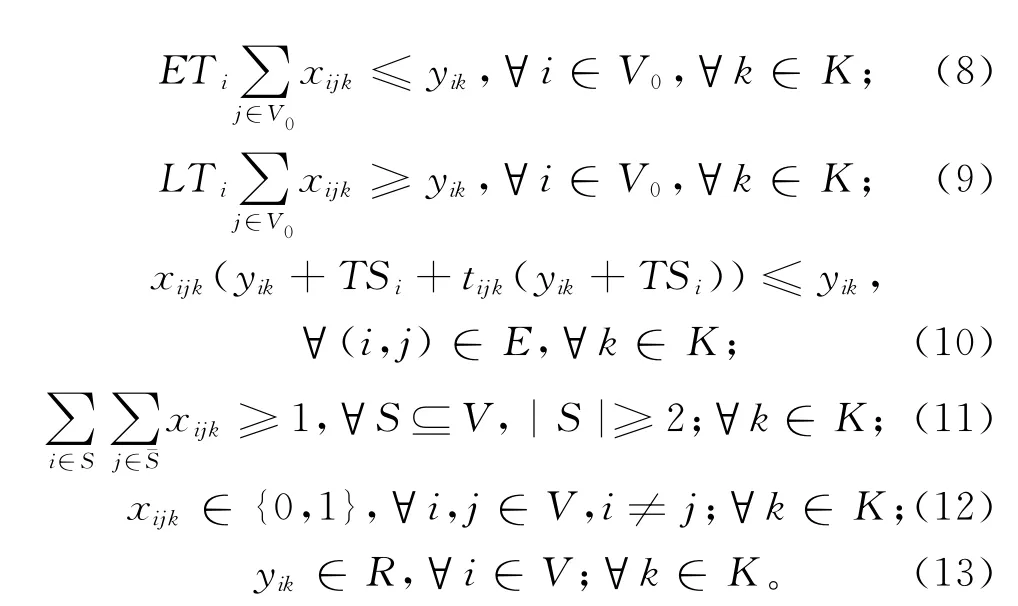
其中：式（1）为主目标函数，优化目标为最小化所使用的车辆数；式（2）为次目标函数，优化目标为最小化车辆总行驶距离；式（3）为载重量约束条件，每辆车所装载的货物总重量不能超过车辆的额定载重；式（4）保证所有顾客均被服务；式（5）限制了对于车辆k进入顾客h后必须离开，保证了路径的连贯性；式（6）和式（7）保证了所有的车辆都从原点出发并回到原点；式（8）和式（9）保证了车辆的开始服务时间必须满足顾客的时间窗约束；式（10）保证了服务开始时间必须满足顾客间的行驶时间；式（11）为消除子回路的约束；式（12）～式（13）表示变量的取值范围。

2 TDVRP问题的并行模拟退火算法设计

求解TDVRP的并行模拟退火算法是在一个初始解的基础上，使用并行计算在解邻域内进行搜索，以得到更优解。本章首先介绍如何获得TDVRP的初始解，然后给出本文使用的邻域搜索算法，并介绍如何将经典的串行模拟退火算法应用于求解TDVRP，最后提出使用主从模式将串行模拟退火算法并行化。

2.1 初始解

本文引用一个小型的启发式算法，采用前向插入 启 发 式 （Push Forward Insertion Heuristic，PFIH）算法生成初始解。Solomon［3］提出解决VRP的PFIH算法的步骤为：随机选取未分配路径的顾客并尝试插入当前路径，检查是否满足能力和时间窗约束，若存在多个可行插入位置，则选择最小插入成本位置插入，将未被分配路径的顾客依次插入到当前路径中，直到当前路径的配送需求超过车辆的配送能力为止，此时一条新的路径形成。重复该流程，直到所有顾客都被分配至路径上为止。在选择未被分配路径的顾客时，Solomon［3］提出优先考虑距离中心仓库最远的顾客作为潜在顾客，Czech［18］提出优先考虑将最早开始时间最小的顾客作为潜在顾客。综合以上两点，本文综合考虑时间窗的宽度与距离的关系，提出时间窗紧致度的概念。

由式（14）可知，某顾客的时间窗越短且距离越远，则Tightness＿of＿time＿window越小，优先考虑将该顾客作为潜在顾客插入当前路径中。

式中A表示时间窗相对于距离的权重系数。

2.2 邻域搜索

邻域搜索过程为在当前解sk的邻域内进行局部搜索产生新的可行解s′k的过程。本文在随机的邻域内整合四种局部搜索方法，对当前路径进行改进，包括路径内搜索（2-opt法和 Or-opt法）和路径间搜索（swap／shift法和2-opt＊法）。算法选择2－opt法［19］、Or－opt法［20］、swap／shift法［21］和2－opt＊法［22］的概率均为1／4。这四种局部搜索方法已被普遍应用于SA算法和其他亚启发式算法中，本节将简要介绍这些邻域搜索算法。

（1）2-opt法［19］该方法通过改变一条路径中顾客的排序来减少路径距离。如果该路径的成本减少，则改进的路径被保留；否则，路径返回修改前的情形。

（2）Or-opt法［20］该方法将一条路径中的m个连续的顾客节点在该路径中重新定位。若m＝1，则意味着将路径中的一个顾客节点在该路径中重定位。

（3）Swap／shift法［21］该方法或者转移一条路径中的顾客到另一条路径，将顾客节点i从路径r1转移到路径r2的顾客节点j和j＋1之间，形成两条新的路径r′1和r′2；或者交换两条不同路径中的两个顾客节点，将路径r1中的顾客节点i与路径r2的顾客节点j交换，即路径r1的顾客节点i移动到路径r2的顾客节点j－1和j＋1之间，将路径r2的顾客节点j移动到路径r1的顾客节点i－1和i＋1之间，形成两条新的路径r′1和r′2。

（4）2-opt＊法［22］在该方法两条路径中分别取1个交换位置，将第1条路径交换位置之后的所有顾客节点与第2条路径交换位置之后的所有顾客节点互换。

2.3 串行模拟退火算法

串行模拟退火算法是基于蒙特卡洛迭代算法进行求解的，由某一高温度开始，利用具有概率突变特性的Metropolis抽样策略，在解空间随机搜索，随着温度的不断下降，重复搜索过程，最终得到问题的全局最优解。SA算法与通常的局部搜索算法相比，其最大的特点是，以一定的概率选择邻域中目标值相对较大（对于最小值问题）的状态，这一点使SA算法成为一种理论上的全局最优算法。SA算法的计算流程如图4所示。

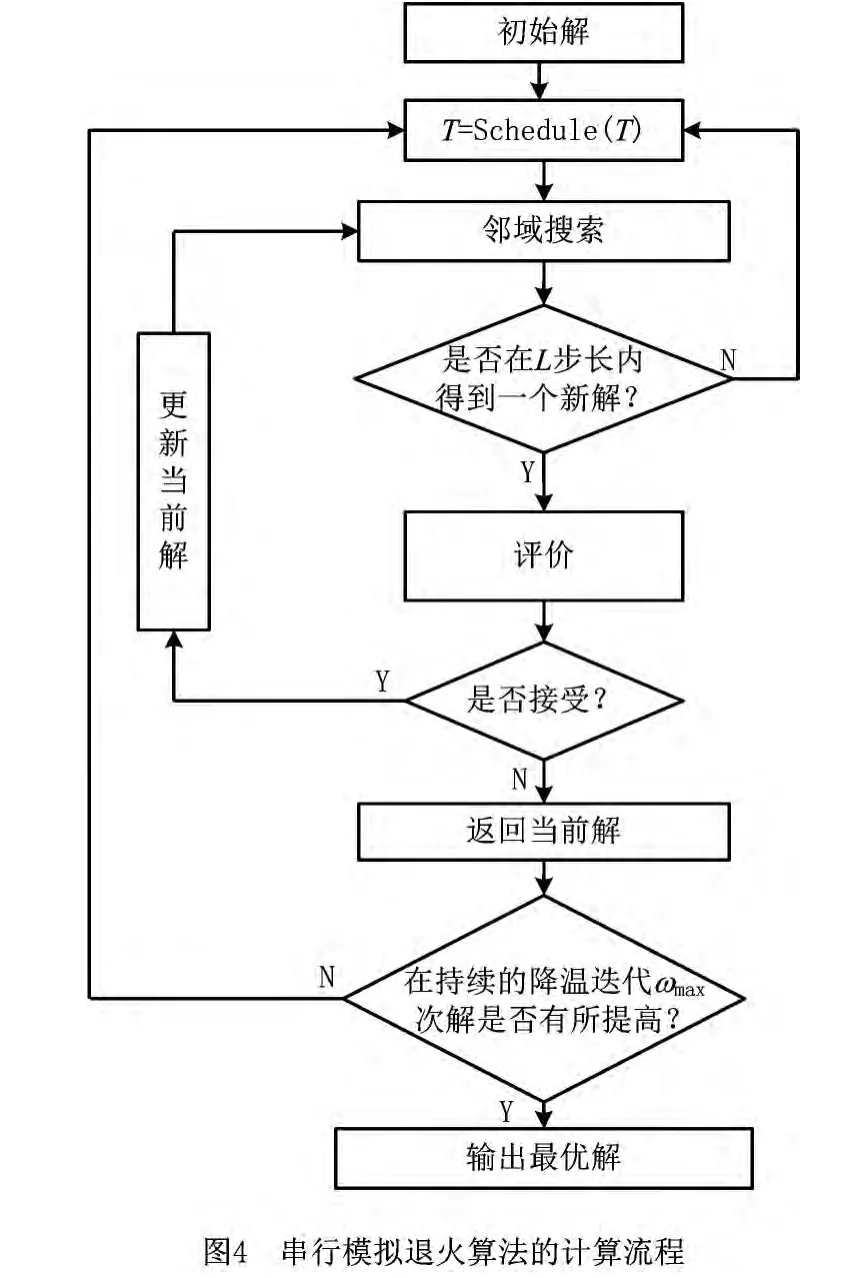
根据串行模拟退火算法的流程，可得求解TDVRP的伪代码如下：

其中：cost（sk）＝σcd（c×n＋emin）＋（1－σ）ctd，Tk＝γ×cost（sk）；sk为可行解；σ为常数，权衡分派成本和行驶成本的参数，σ∈［0，1］；cd为车辆k的分派成本；c为在此解下所使用的车辆数量；n为顾客数量；emin为在最短路径中的顾客数量；ct为单位距离的行驶成本；d为路径的总行驶距离；γ＜1且为常数；β为降温比率，β＜1且为常数；k为温度计数器；ω为温度的持续降低而当前解保持不变的计数器；l为迭代次数。

虽然传统的串行SA具有原理简单、使用灵活、适合求解出优化问题的全局最优或近似全局最优解等优点，但它是以严密的退火计划为保证的，具体地讲，就是足够高的初始温度、缓慢的退火速度、大量的迭代次数及同一温度下足够的扰动次数。因此，SA算法的效率问题一直是算法真正走向实际应用的障碍。由此可见，需要对经典的SA算法进行改进，提高算法的收敛速度，加速优化过程。

2.4 主从模式的并行化

本节将SA算法进行并行化处理，构建p-SA算法，以加快算法的收敛速度。目前已有一些方法实现了模拟退火算法的并行处理［23］，如：移动加速、并行移动、多马尔科夫链、推测性计算。其中，多马尔科夫链是最常用的并行方法。该方法是将经典的串行模拟退火算法中的一条马尔科夫链分裂为在一定时间内独立生长、又可以适当交换信息的多条马尔科夫链，以取得可扩展的并行性，打破经典SA算法并行化的瓶颈。此外，通过记忆马尔科夫链的最优值，并按照一定的时间间隔对不同的马尔科夫链得到的最优值进行交换，可加快优化的过程。马尔科夫链策略分为同步和异步两种。

当采用异步马尔科夫链策略时，在每个确定的周期或各自搜索结束后对比最终状态。该方法可以实现每个线程对应一个模拟退火链，并进行独立的运行。在每个线程运算结束后交流线程的各自局部最优解，从局部最优解中再选择全局最优解。当采用同步马尔科夫链策略时，每个线程获得初始解s0后独立地运行马尔科夫链。当温度确定时，每个线程实际上是一个Metropolis过程。当经过一段固定的间隔周期、到达某个确定的中间温度时，模拟退火链比较其当前局部最优解sp及其对应的成本值cost（sp），p＝0，1，…，W－1。比较W个线程的cost（sp）值后，如果线程pΩ的成本值最小，则在下一个温度水平下，将当前的局部最优解作为各个线程的初始解。假如此时有多于两个的局部最优解，，…，则任选一个即可，该选择过程不影响最终的结果。如果将每个模拟退火链当作遗传算法中的不同个体，则该过程可以理解为遗传算法的交叉过程，用于选择种群的演化。

采用p-SA算法提高了SA算法的求解速度，既保证了整个算法有较大规模的并行粒度，又使得在确定的温度水平下，上一个分线程搜索的结果传递给下一个分线程，实现了搜索信息的融合。图6为求解TDVRP的并行模拟退火算法流程。

根据p-SA算法流程，可得求解TDVRP问题的伪代码如下：

对于p-SA算法，线程PW－1在for循环内（21～29行）需要经过n步信息交换，对于每一步信息交换，有（W－1）－1个信息量为O（n）的信息被发送和接收，因此执行整个for循环的时间成本为n2（n＋（W－1）－1）。16行和31～32行的时间成本为pn。因此，p－SA算法的总时间成本不超过pn＋kn2（n＋（W－1）－1），其中k为降温次数，则时间复杂度为pn＋kn2（n＋（W－1）－1）＝O（n3＋（W－1）n2）。

3 算法性能比较分析

3.1 测试环境

本文的测试环境如下：Intel（R）Core（TM）i7-2 620M，2.70GHz CPU；4GB 内 存；Windows 7 32bit操作系统；编程环境为JDK7。

3.2 测试算例的构造

测试算例全部来自Figliozzi［4］提供的标准测试问题，Figliozzi测试数据库是在Solomon提供的56个100顾客规模的标准测试问题的基础上增加了4组时间依赖函数。Solomon（Dr.Solomon提供Solomon测试数据库的下载：http：／／w.cba.neu.edu／～msolomon／problems.htm）测试数据库采取了数据集R101（随机分布）、C101（堆分布）、RC101（半堆分布）、R201（随机分布）、C201（堆分布）和 RC201（半堆分布）进行测试，具有以下特点：①数据集R101和R201中节点的地理位置是随机生成的；②数据集C101和C201中节点的地理位置为聚类分布，数据集RC101和RC201中节点的地理位置是混合随机聚类分布；③数据集R101，C101和RC101的整个计划时间较短，每条路径中只能安排几个顾客（约5～10个顾客）；而数据集 R201，C201和RC201则有一个较长的计划时间，且其车辆装载容量比数据集R101，C101和RC101的车辆装载容量大很多，因此在每条路径中可以安排更多的顾客（增加30多个）。Figliozzi假设一天存在早高峰和晚高峰，并假设中心仓库的时间窗［ET0，LT0］代表车辆／司机的一天工作时间，并均匀分成5份，则时间间隔为：［0，0.2LT0）；［0.2LT0，0.4LT0）；［0.4LT0，0.6LT0）；［0.6LT0，0.8LT0）；［0.8LT0，LT0］。

本文设置了4组时间依赖函数如表1所示（通过与Dr.Figliozz邮件往来，本文纠正了原论文中（a）和（b）文字描述与表（a）和（b）内容不一致的小错误），分别为：①组：车辆离开中心仓库时正好为一天的早高峰时间，接下来的1／5时间为中午时间，拥堵状况得到了缓解，再接下来的1／5时间在晚高峰之前，车辆行驶速度较快，最后的1／5时间为晚高峰时间；②组：车辆离开中心仓库的时间非常早，在第一个1／5时间还没有发生拥堵，接下来的1／5时间车辆行驶中伴随着早高峰，到中午时拥堵状况得到了缓解，接下来的1／5时间内遇到了晚高峰，最后的1／5时间内车辆行驶中晚高峰已经过去；③组：车辆离开中心仓库的时间非常早，以致在前1／2的工作时间内均未发生拥堵，在后1／2的工作时间内遇到了严重的早高峰；④组：车辆离开中心仓库的时间恰逢早高峰，在前1／2的工作时间内发生早高峰拥堵，在后1／2的工作时间内早高峰拥堵已经过去。

表1 Figliozzi时间依赖函数

续表1

3.3 算法参数的确定

并行模拟退火算法需要确定的参数有：线程数W，式（14）中时间窗相对于距离的权重系数Α，图5中的σ，温度与成本关系常数γ，温度下降常数β，和继续迭代的次数ωmax。根据经验公式，W＝核数×2＋2［24］，则本文中线程数为6。取时间窗相对于距离的权重系数Α＝1 000。由物理退火可知，退火过程是由快到慢，而且越到最后越慢，根据这一特性，β＝0.8～0.999［25］。

采取试算法确定p-SA算法的最优参数值，即每次给出某参数的一组数值，固定其他参数，根据算例的计算结果确定该参数的最优取值。实验过程验证了本文的预期，较高的降温比率对应于缓慢的降温过程，因此需要更多的迭代次数直到算法终止。得到各参数的取值如表2所示。

表2 并行模拟退火算法的参数取值

3.4 算法性能分析

为验证算法的性能，使用Figliozzi数据库求解带硬时间窗的TDVRP，计算结果如表3～表7所示，该结果包括所需车辆数和车辆行驶距离两部分，每一单元格的上半部分为所需车辆数、下半部分为行驶距离。主目标函数为降低车辆的数量，次目标函数为减少车辆的总行驶距离。表中Best known为目前国际上公布的已知最优解，Donati等［12］使用多蚁群系统求解，Figliozzi［4］提出使用迭代路径构建 和 提 高 （Iterative route construction and improvement，IECI）算法求解。对比在单位速度、（a）组、（b）组、（c）组和（d）组下的 TDVRP结果可知，当行驶速度提高时，所需车辆数量有明显的降低，但相对而言行驶距离的改变不是很明显。

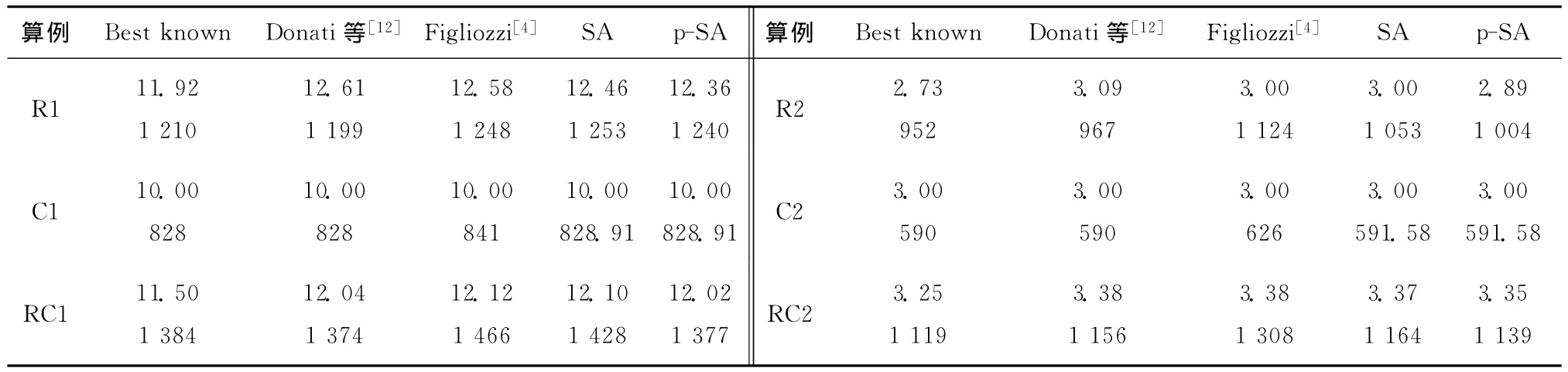
表3 TDVRP结果——单位速度下的Solomon测试数据库

由表3可知，如果速度为单位速度，则TDVRP退化为VRPTW。p-SA算法与Donati等［12］算法基本 相 当，优 于 Figliozzi［4］算 法，但 均 次 于 Best known。本文的p-SA算法包含6个线程，其中1个主线程使用PFIH算法求得初始解，在整个算法中不执行SA计算，只负责在搜索环节监控过程并接收从W－1线程返回的当前局部最优解，并将当前全局最优解发送给各个从线程，执行下一轮并行计算。5个从线程接收当前全局最优解，独立地执行邻域搜索过程，周期性地交换当前最优解的信息，比较自身解和上一个从线程计算的最优解。比较SA算法和p-SA算法可知，在同样的计算机配置下，p－SA算法的计算速度约是SA算法的5倍，优势明显。

由表4～表7可知，在时间依赖函数为①～④情形下的TDVRP：①比较最优解的质量可知，SA算法和p-SA算法的计算结果均优于Figliozzi［4］算法；②对于同一个TDVRP测试数据集，虽然p-SA算法比Figliozzi［4］算法可以更快地求得最优解，但由于算法使用不同配置的计算机求解，56个测试算例的计算时间无法比较。SA算法和p-SA算法使用相同配置的计算机求解同一个TDVRP测试数据集，p-SA算法的计算时间约为SA 算法的1／5-1／4，因此p-SA算法近似达到了5倍的加速比。

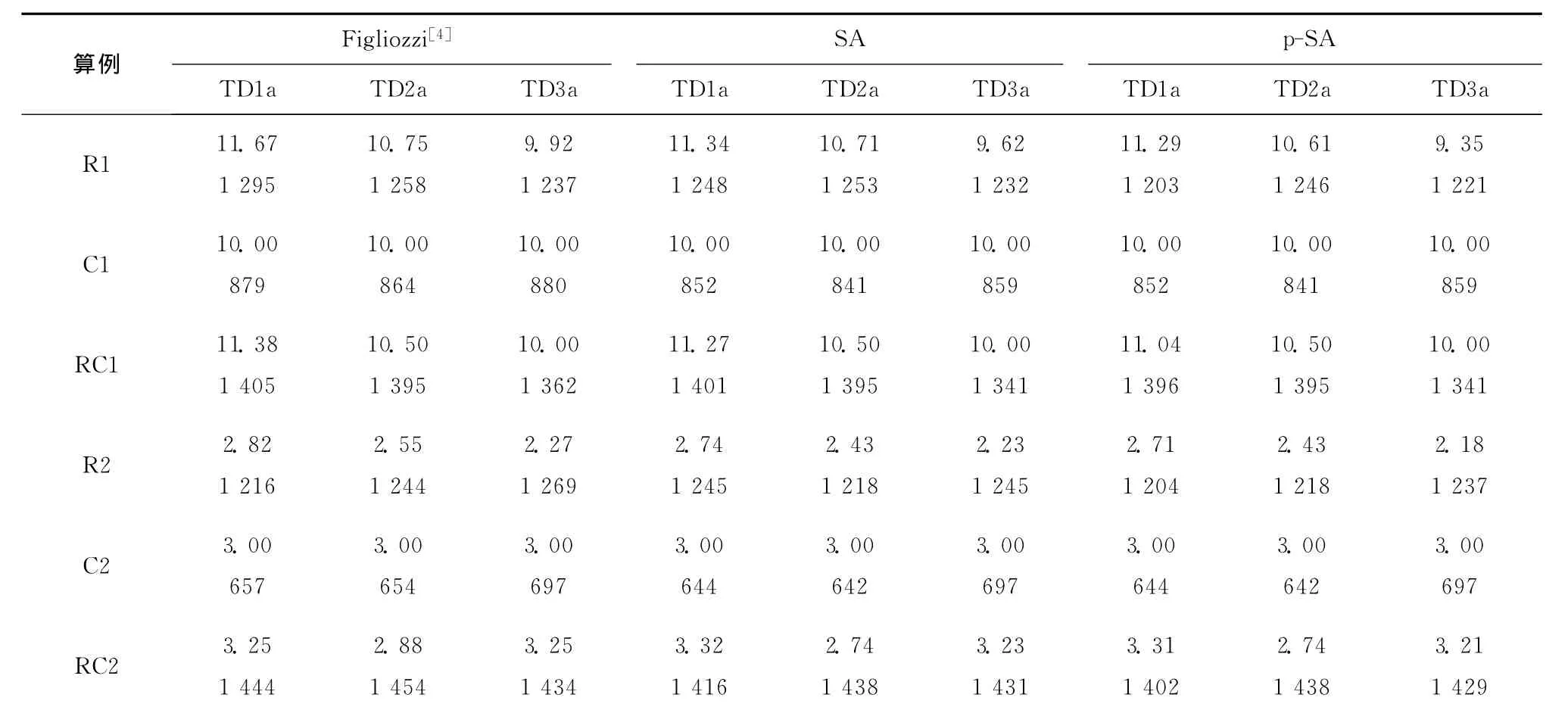
表4 TDVRP结果——①组时间依赖函数

表5 TDVRP结果——②组时间依赖函数

表6 TDVRP结果——③组时间依赖函数

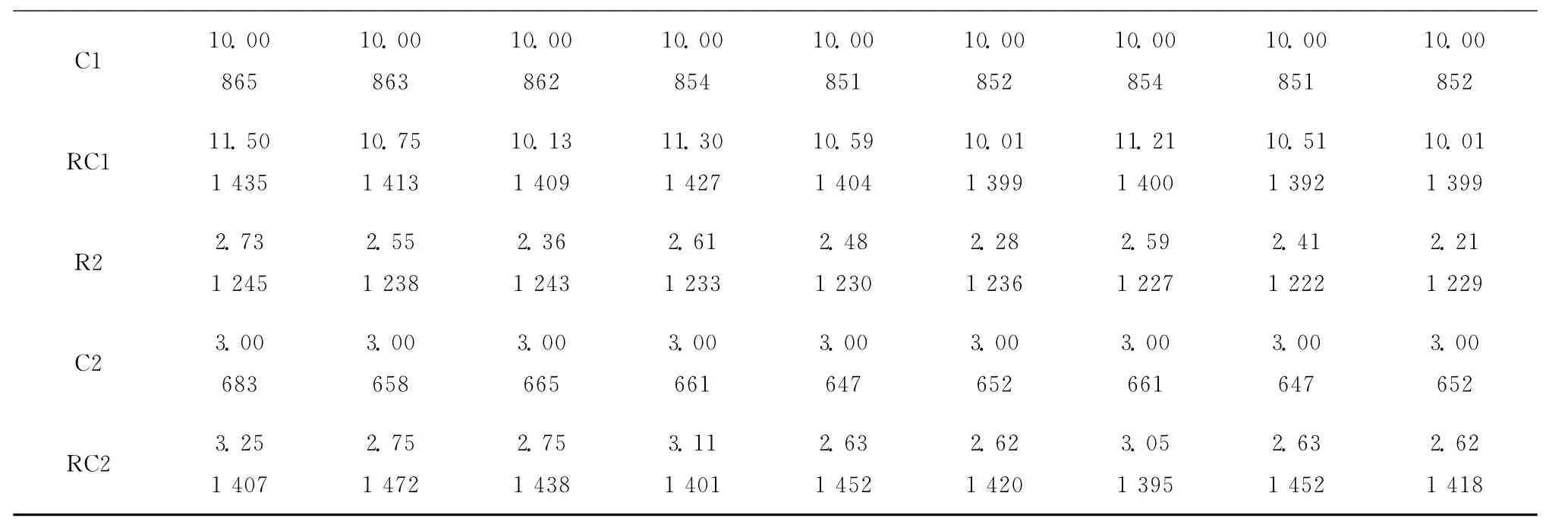
续表6

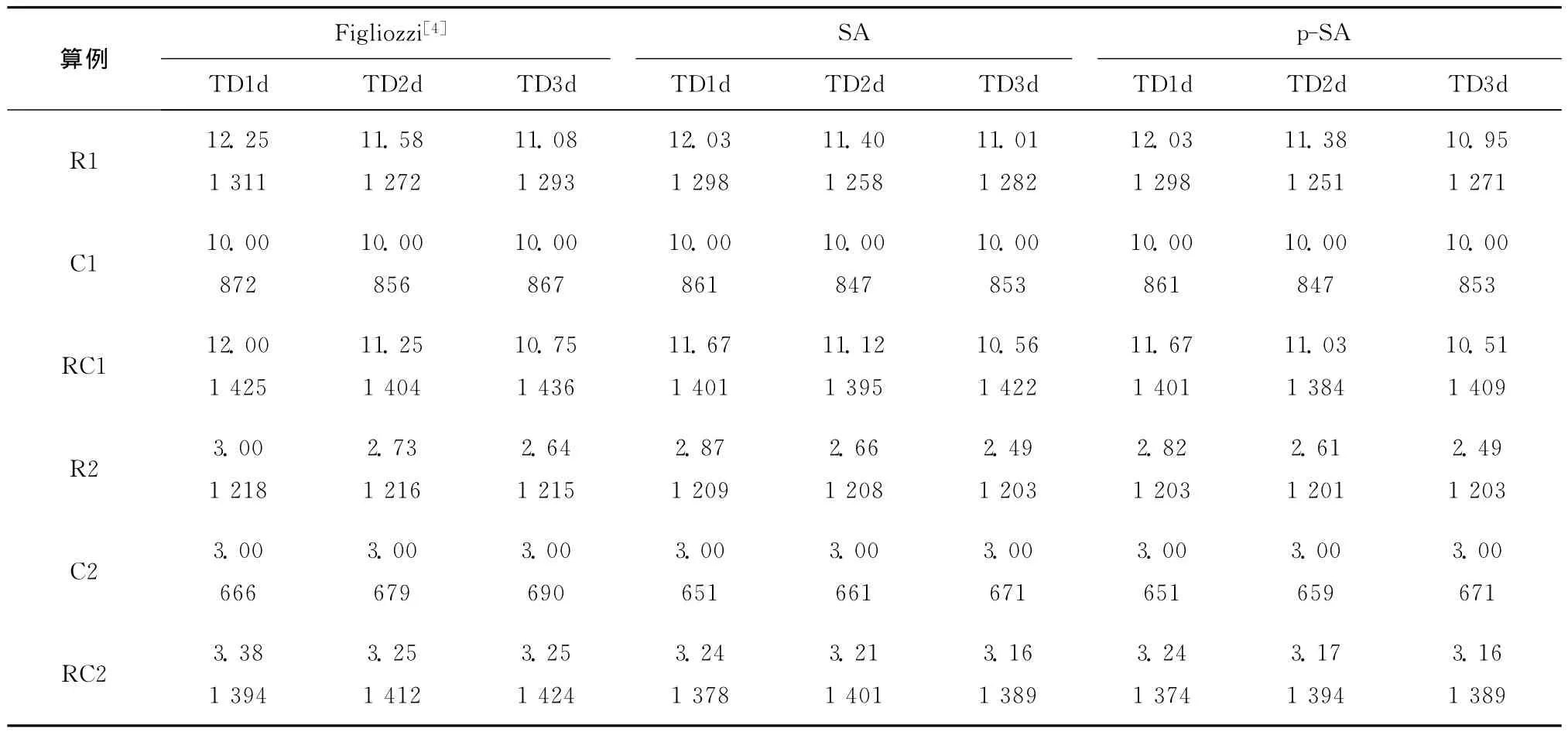
表7 TDVRP结果——④组时间依赖函数

4 结束语

时间依赖型车辆路径问题是应用非常广泛的NP-hard组合优化问题。在过去几年间，设计有效的算法来求解TDVRP，引起了许多学者的研究兴趣。然而，目前已经发表的科技论文由于顾客规模不同、目标函数不同和约束条件不同，无法进行解的质量和算法性能的比较。自Figliozzi发布标准测试数据库后，使不同算法间的比较成为可能。本文根据TDVRP的特性，对经典的串行模拟退火算法进行改进，提出并行模拟退火算法。该算法在不需要修改算法结构的情况下，可计算速度恒定和时间依赖函数情形下的TDVRP。首次使用Figliozzi数据库对p-SA算法性能进行测试，与已知国际最优解以及其他相关算法所得结果进行比较可知，p-SA算法求解TDVRP问题是有效的，能够以较快的收敛速度在可接受的计算时间内收敛到满意解。在主从模式的并行框架下，当使用6个线程时，相对于SA算法，p-SA算法近似达到了5倍的加速比。后续将研究速度可变情形下的能源消耗最小的路径、行驶路程最短的路径、总成本最低的路径的求解问题等。

［1］ DANTZIG G B，RAMSER J H.The truck dispatching problem［J］.Management Science，1959，6（1）：80-91.

［2］ BEASLEY J E.Adapting the savings algorithm for varying inter-customer travel times［J］.Omega，1981，9（6）：658-659.

［3］ SOLOMON M M.Algorithms for the vehicle routing and scheduling problems with time window constraints［J］.Operations Research，1987，5（2）：254-265.

［4］ FIGLIOZZI M A.The time dependent vehicle routing problem with time windows：Benchmark problems，an efficient solution algorithm，and solution characteristics［J］.Transportation Research Part E：Logistics and Transportation Review，2012，48（3）：616-636.

［5］ MALANDRAKI C，DASKIN M S.Time dependent vehicle routing problems：Formulations，properties and heuristic algorithms［J］.Transportation Science，1992，26（3）：185-200.

［6］ PARK Y B，SONG S H.Vehicle scheduling problems with time-varying speed［J］.Computers ＆Industrial Engineering，1997，33（3）：853-856.

［7］ PARK Y B.A solution of the bicriteria vehicle scheduling problems with time and area-dependent travel speeds［J］.Computers ＆Industrial Engineering，2000，38（1）：173-187.

［8］ HILL A V，BENTON W，Modelling intra-city time-dependent travel speeds for vehicle scheduling problems［J］.Journal of the Operational Research Society，1992，43（3）：343-351.

［9］ ICHOUA S，GENDREAU M，POTVIN J Y.Vehicle dispatching with time-dependent travel times［J］.European Journal of Operational Research，2003，144（2）：379-396.

［10］ WOENSEL T V，KERBACHE L，PEREMANS H，et al.Vehicle routing with dynamic travel times：aqueueing approach［J］.European Journal of Operational Research，2008，186（3）：990-1007.

［11］ DONATI A V，CAMBARDELLA L M，CASAGRANDE N，et al.Time dependent vehicle routing problem with an ant colony system［EB／OL］.Manno，Switzerland：Istituto Dalle Molle Di Studi Sull Intelligenza Artificiale（IDSIA），2002，［2014-02-12］.http：／／people.idsia.ch／～roberto／papers／IDSIA-02-03.pdf.

［12］ DONATI A V，MONTEMANNI R，CASAGRANDE N，et al.Time dependent vehicle routing problem with a multi ant colony system［J］.European Journal of Operational Research，2008，185（3）：1174-1191.

［13］ WANG Zhengguo，LIU Zhenyuan，WANG Hongwei，et al.Reactive tabu search algorithm for time-dependent vehicle routing problem with backhauls［J］.Computer Integrated Manufacturing Systems，2006，12（9）：1453-1458（in Chinese）.［王正国，刘振元，王红卫，等.适应性禁忌搜索算法求解带回程的时变速度车辆路径问题［J］.计算机集成制造系统，2006，12（9）：1453-1458.］

［14］ LI Yanfeng.Research on vehicle routing problem in time-varing network［D］.Chengdu：Southwest Jiaotong University，2008（in Chinese）.［李妍峰.时变网络环境下车辆调度问题研究［D］.成都：西南交大大学，2008.］

［15］ DUAN Zhengyu，YANG Dongyuan，WANG Shang.Improved ant colony optimization algorithm for time-dependent vehicle routing problem［J］.Control Theory ＆ Applications，2010，27（11）：1557-1563（in Chinese）.［段征宇，杨东援，王上.时间依赖型车辆路径问题的一种改进蚁群算法［J］.控制理论与应用，2010，27（11）：1557-1563.］

［16］ KUO Y Y.Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem［J］.Computers ＆Industrial Engineering，2010，59（1）：157-165.

［17］ DESROCHERS M，LENSTRA J K，SAVELSBERGH M W P，et al.Vehicle routing with time windows：optimization and approximation［J］.Vehicle Routing：Methods and Studies，1988，16：65-84.

［18］ CZECH Z J，CZARNAS P.Parallel simulated annealing for the vehicle routing problem with time windows［C］／／Proceedings of the 10th Euromicro Workshop on Parallel，Distributed and Network-based Processing.Washington，D.C.，USA：IEEE，2002：376-383.

［19］ LIN S.Computer solutions of the traveling salesman problem［J］.Bell System Technical Journal，1965，44（10）：2245-2269.

［20］ OR I.Traveling salesman-type combinatorial problems and their relation to the logistics of regional blood banking［D］.Saint Paul：the Northwestern University，1976.

［21］ CHEN J F，WU T H.Vehicle routing problem with simultaneous deliveries and pickups［J］.Journal of the Operational Research Society，2006，57（5）：579-587.

［22］ POTVIN J Y，ROUSSEAU J M.An exchange heuristic for routeing problems with time windows［J］.Journal of the Operational Research Society，1995，46（12）：1433-1446.

［23］ CHANDY J A，KIM S，RAMKUMAR B，et al.An evaluation of parallel simulated annealing strategies with application to standard cell placement［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，1997，16（4）：398-410.

［24］ RICHTER J，NASARRE C.Windows via C／C＋＋ ［M］.5th ed.，Redmond，USA：Microsoft Press，2011：446.

［25］ ROTHMAN D H.Nonlinear inversion，simulated annealing，and residual statics estimation［J］.Stanford Exploration Project Rep，1984，9（41）：297-326.