灰色聚类分析法在投标决策中的应用

龙 伟 邓 龙

（1.三峡大学 水利与环境学院，湖北 宜昌 443002；2.武汉大学 水利水电学院，武汉 430072）

施工企业在投标时，首先必须从众多的招标项目中，选择适合企业自身条件，能发挥企业自身优势且赢利较多的工程项目进行投标［1－3］，这就是投标项目优选决策.目前，我国的地质灾害防治工程除已经出现险情的应急项目外，大多数情况下，往往都是一批项目同时批复、同时招标，例如三峡库区地质灾害防治工程，国家就是采取分期批复、分期实施的，因此同期招标的项目一般较多.由于影响地质灾害防治工程投标的因素很多，大多数因素定性容易而定量分析困难，而且各项目的情况千差万别，这就要求投标者在综合考虑各种影响因素的基础上，对每一个招标的工程项目进行科学而全面的分析，从中选取最佳的工程项目进行投标，这对施工企业获取利润，开拓市场具有十分重要的意义.

1 投标项目优选决策的常用方法

目前，投标项目选择的常用方法有：层次分析法、决策树分析法等.层次分析法（AHP）［4］是美国运筹学家沙旦（T.L.Saaty）于上世纪70年代提出的，是一种定性与定量分析相结合的多目标决策分析方法.层次分析法首先确定参加投标的影响因素，然后针对具体项目对所有影响因素进行打分，根据过去的经验当分值大于一定数值就投标，否则放弃投标.由于影响工程项目因素的复杂性、多样性和人们判断的模糊性，往往不同的人判断影响因素不一样，不同的人对影响因素打分不一样，可能导致的结果不一样.决策树分析法［5］是适宜于风险型决策分析的一种简便易行的实用方法，是通过利润与中标概率综合分析，通过损益值与该损益值发生的概率的乘积在状态节点之和的大小来决定该方案的取舍.

2 灰色聚类分析法在投标决策中的应用

灰色聚类分析法［6－8］是将聚类对象与不同聚类指标所拥有的白化函数，按n个灰类进行归纳，从而判断聚类对象属哪一类的灰色统计方法.灰色聚类分析法是指先把预测问题化为灰色聚类分析问题，即把预测对象视为聚类对象，把影响预测对象的相关因子视为聚类指标，把所需要预测（或判断）的类别（或等级）可视为聚类灰数（即灰类），把影响预测对象的各相关因子的实际取值视为聚类白化数，然后按灰色聚类分析方法确定灰类的白化权函数与标定聚类权重后，计算聚类系数，构成聚类行向量，按聚类行向量分量大小把聚类对象（预测对象）进行聚类（或判断归纳），从而达到预测的目的.

2.1 建立层次结构图

在地质灾害防治工程投标项目优选决策时，在综合分析地质灾害防治工程特点、投标人情况后，对影响投标的因素进行归纳，建立地质灾害防治工程投标决策影响因素层次结构图，如图1所示.通过灰色理论的聚类评估知识进行综合评判，最后决定投标项目.

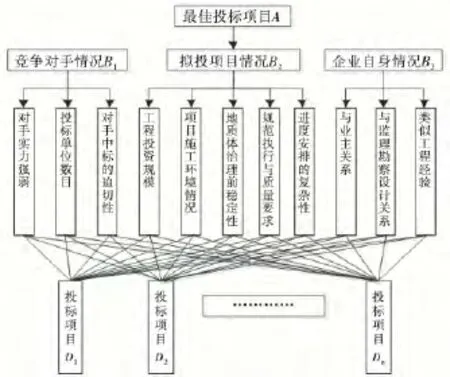
图1 地质灾害防治工程投标决策影响因素层次图

地质灾害防治工程投标决策影响因素层次图由4层组成，分目标层A、准则层B、因素层C、选择层D.准则层B包括企业自身情况、竞争对手情况、拟投项目情况.准则层B的3个分项又包括若干子项，子项构成因素层C.下面分别对因素层中各项的意义、量化依据、量化结果进行说明，见表1.

在表1中，许多因素本身都是通过定性描述的，采用1～9标度法进行量化具有一定的模糊性，例如对手中标的迫切性C3，可分（不、有点、较为、非常、极为）迫切等，分别用1、3、5、7、9表示，相邻两个程度的中间值分别用2、4、6、8表示.有些因素（如C8进度安排的复杂性）进行量化时考虑的方面比较多，在量化时将各个方面分别赋值，然后得出该因素的综合量化值.

2.2 建立分析模型

利用灰色理论的知识对投标项目进行综合评判.

1）建立量化矩阵P

式中，Pij为子因素的量化结果；i为第i个待投标项目，i＝1，2，…，m；j为第j个子因素，j＝1，2，…，n.

在量化矩阵中，要求每个量化结果对目标层A的影响是一致的，如果不一致要进行转化，使其成为影响一致的矩阵.即在P矩阵中，每个pij对于目标层的影响或者都是越大越好，或者都是越小越好.矩阵的这一性质称为矩阵极性的一致性.

2）定义3个灰类

令k＝1为第一灰类（上灰类），即“应该投标”；k＝2为第二灰类（中灰类），即“可以投标”；k＝3为第三灰类（末灰类），即“不应该投标”.

3）确定灰类的白化函数

①上灰类（应该投标），灰数⊗1∈［a1，∞），第一灰类白化函数F1如式（2），见图2.

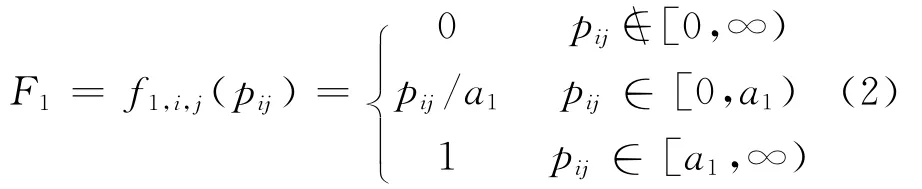
②中灰类（可以投标），灰数⊗2∈［0，2a2］，第二灰类白化函数F2如式（3），见图3.

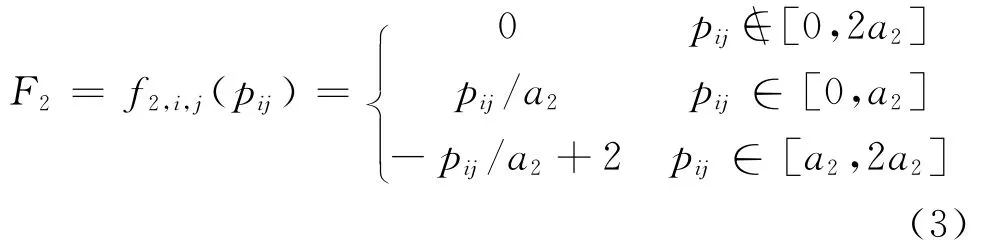
③末灰类（不应该投标），灰数⊗3∈［0，2a3］，第三灰类白化函数F3如式（4），见图4.

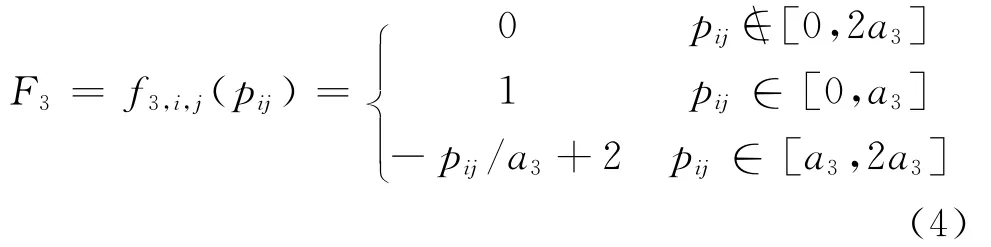
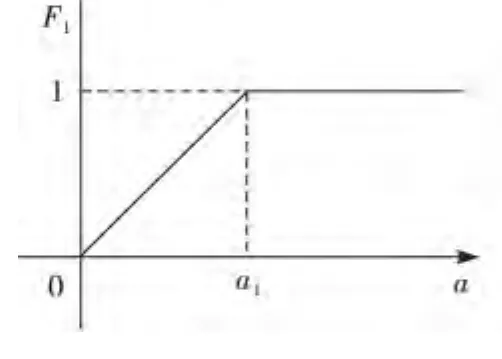
图2 第一灰类白化函数

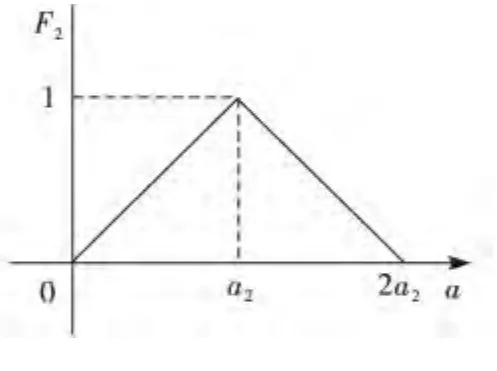
图3 第二灰类白化函数

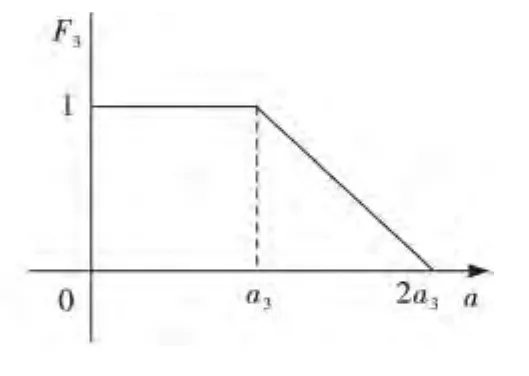
图4 第三灰类白化函数

上述3个公式中，a1、a2、a3分别为3个灰类的阀值.a1、a2、a3的值可以根据某种经验或准则，用类比的方法确定；也可以从评价矩阵P中寻找最大、最小或中等值，作为a1、a2、a3的相对阀值.

4）确定各评价指标的权重

利用层次分析法中的判断矩阵（AHP法），通过两两比较判断矩阵，求解判断矩阵的特征向量的方法确定其相对权重.判断矩阵采用1～9标度法.比如，某一层有E1，E2，…，En元素，针对上一层R中元素Rk的标度数值见表2.

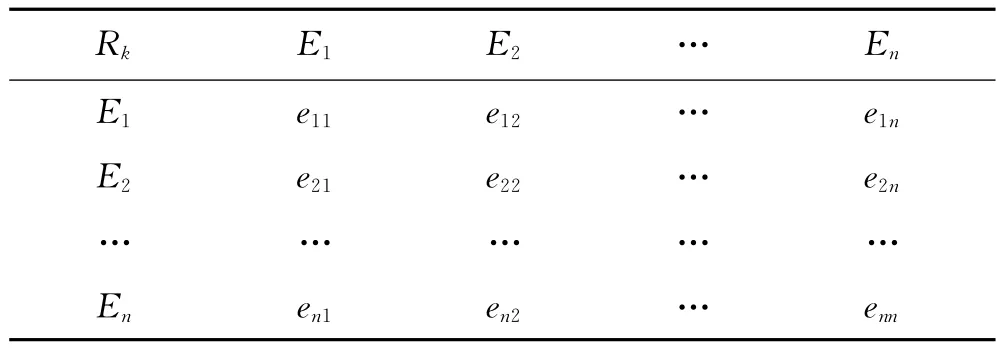
表2 判断矩阵R－E

表2中，eij是对于Rk而言，Ei对Ej的相对重要性的数值表示，通常eij取1，2，3，…，9及它们的倒数，其中：eii＝1，eji＝1／eij（i，j＝1，2，…，n），eij＞0.

1～9标度方法的含义如下：

eij＝1表示Ei与Ej同等重要；eij＝3表示Ei比Ej稍微重要；eij＝5表示Ei比Ej明显重要；eij＝7表示Ei比Ej强烈重要；eij＝9表示Ei比Ej极端重要；eij＝2，4，6，8分别表示重要程度介于上述两相邻奇数之间.

为了保证判断矩阵结果的一致性，要求eij＝eik／ejk，由于人的主观性影响，很难做到eij＝eik／ejk，为保证得到的权重的合理性，要对每一个判断矩阵进行一致性检验，以观察其是否具有满意的一致性.否则，要修改判断矩阵，直到满足一致性要求.

一致性检验的步骤如下：

①计算一致性指标CI.一致性指标CI＝（λmax－n）／（n－1）.显然，当判断矩阵具有完全一致性时，CI＝0.λmax－n越大，CI越大，矩阵的一致性越差.

②引入平均随机一致性指标RI.为了检验判断矩阵是否具有满意的一致性，需要将一致性指标CI与平均随机一致性指标RI进行比较.判断矩阵的维数越大，判断的一致性将越差，故应放宽对高维判断矩阵一致性的要求.对于1～11阶的判断矩阵，平均随机一致性指标RI值见表3.

表3 RI值表

对于1阶、2阶判断矩阵，平均随机一致性指标RI只是形式上的，按照判断矩阵的定义，1阶、2阶判断矩阵总是完全一致的.当阶数大于2时，判断矩阵的一致性指标CI，与同阶平均随机一致性的指标RI之比称为判断矩阵的随机一致性比例，记为CR.

③计算随机一致性比例.随机一致性比例CR＝CI／RI，当CR＜0.1时，一般认为判断矩阵具有满意的一致性.否则，需要对判断矩阵进行调整.判断矩阵的特征向量经过归一化处理后即得各个指标的权重W＝（W1，W2，……，Wn）.

5）确定灰类评估值

指标的权重确定后，把量化矩阵中的每个量化结果利用白化函数处理，然后聚类分析，聚类分析的结果：

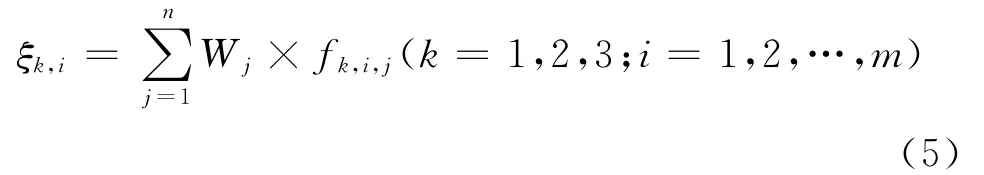
6）项目灰类的评判

根据最大隶属度原则，项目i的灰类k为

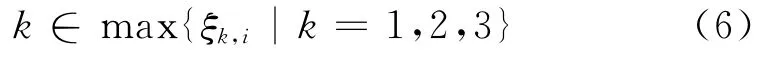
3 地质灾害防治工程算例

某施工企业有4个待投标工程：Ⅰ（业主甲、滑坡防治工程、投资1 500万元）、Ⅱ（业主甲、库岸防治工程、投资1 100万元）、Ⅲ（业主乙、滑坡防治工程、投资2 000万元）、Ⅳ（业主丙、危岩体防治工程、投资2 800万元）.工程实践中，施工企业考虑防治工程Ⅳ投资最大，将其作为重点投标项目，中标后由于施工经验不足，滑坡体稳定性较差等原因造成该项目赢利低.以下采用聚类分析法确定在上述4个项目中应该优选投标的项目.

经过对4个项目进行分析，建立如图1所示的地质灾害防治工程投标决策影响因素层次图，并根据表1对因素层的子因素进行量化，量化的结果见表4.

表4 投标项目影响子因素量化结果表

1）极性一致化与数据无量纲化

将表4形成的矩阵进行一致性转化，即上述指标均要求越大越好，如果评价指标是越小越好，则按式（6）进行一致性转化，结果见表5.

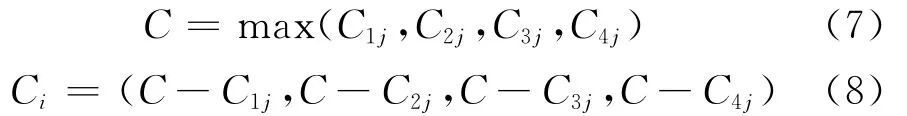
表5 极性一致化的子因素量化结果表

由于表5中部分数据为有量纲数据，将表5中每行除以第二行使其无量纲化，无量纲子因素量化结果见表6.

表6 无量纲化子因素量化结果表

2）建立3个灰类的白化函数并计算白化结果

①确定各个灰类的阀值向量ak，j

i）上灰类白化函数F1＝f1，i，j（a1，j，∞）.其中a1，j＝（a1，1，a1，2，a1，3，a1，4，a1，5，a1，6，a1，7，a1，8，a1，9，a1，10，a1，11）＝（1.20，1.00，1.00，2.55，1.00，1.00，3.00，1.00，1.75，1.29，1.67）.

ii）中灰类白化函数F2＝f2，i，j（0，a2，j）.其中a2，j＝（a2，1，a2，2，a2，3，a2，4，a2，5，a2，6，a2，7，a2，8，a2，9，a2，10，a2，11）＝（1.00，0.50，0.67，1.82，0.67，0.98，2.00，0.50，1.00，1.00，1.33）.

iii）末灰类白化函数F3＝f3，i，j（0，a3，j）.其中a3，j＝（a3，1，a3，2，a3，3，a3，4，a3，5，a3，6，a3，7，a3，8，a3，9，a3，10，a3，11）＝（0.40，0.25，0.33，1.36，0.33，0.96，1.00，0.25，0.50，0.29，1.00）.

②分别建立3个灰类的白化函数

i）上灰类白化函数F1＝f1，i，j（a1，j，∞），具体白化函数见式（1）.

ii）中灰类白化函数F2＝f2，i，j（0，a2，j，），具体白化函数见式（2）.

iii）末灰类白化函数F3＝f3，i，j（0，a3，j），具体白化函数见式（3）.

③3个灰类的白化结果分别见表7～9.

表7 上灰类白化结果F1表

表8 中灰类白化结果F2表

表9 末灰类白化结果F3表

3）确定各个指标的权重

在地质灾害防治工程投标决策影响因素层次图（如图1）中，相对于目标层A而言，准则层B的各个指标Bi之间的相对重要性关系如矩阵A－B，见表10.相对于准则层B而言，因素层C的各个指标Ci之间的相对重要性关系如矩阵B1－C、B2－C、B3－C，分别见表11～13.矩阵极性一致性判断分别见各表下计算情况.

①判断矩阵A－B

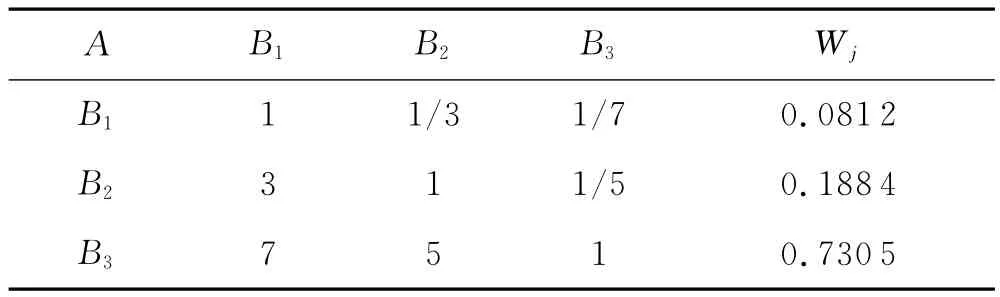
表10 判断矩阵A－B

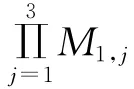
＝0.363 4，同理可求：＝0.843 4，

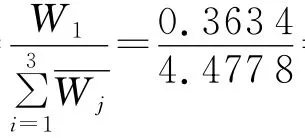
特征向量W＝（0.081 2，0.188 4，0.730 5）.

CR＝CI／RI＝0.062 5＜0.10，符合一致性要求.

②同①步骤可求判断矩阵B1－C如下：

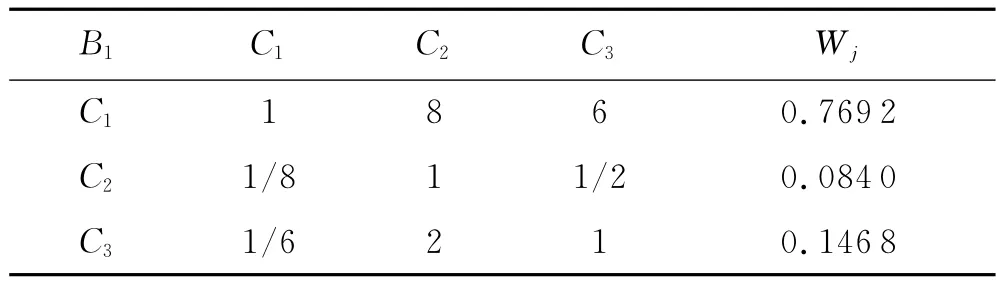
表11 判断矩阵B1－C

CR＝CI／RI＝0.018 2＜0.10，符合一致性要求.

③同理可求判断矩阵B2－C如下：

表12 判断矩阵B2－C

CR＝CI／RI＝0.025 1＜0.10，符合一致性要求.

④同理可求判断矩阵B3－C如下：

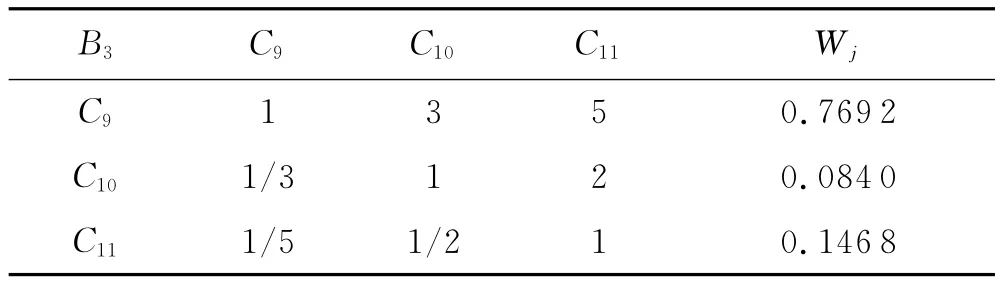
表13 判断矩阵B3－C

CR＝CI／RI＝0.003 5＜0.10，符合一致性要求.

⑤层次总排序及一致性检验.同一层次对总目标的总排序计算见表14.

表14 总排序表

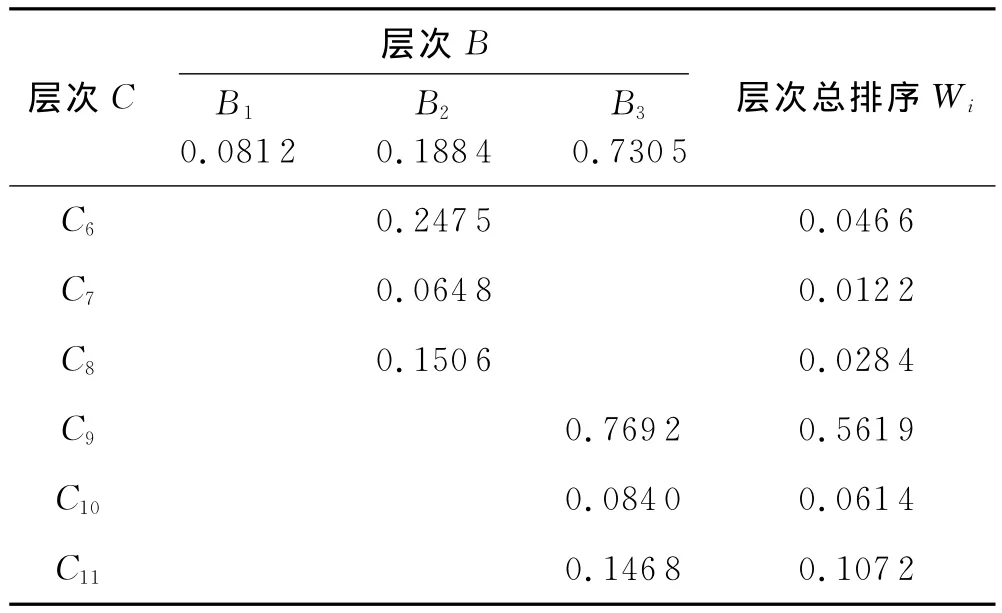
续表14 总排序表

4）聚类分析

计算出总加权值后，根据灰类白化结果（表7～9），利用公式（4）

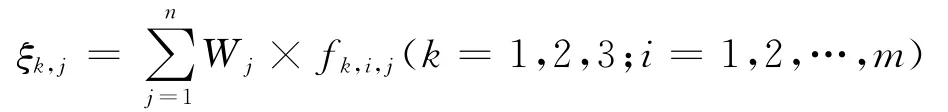
进行聚类分析，聚类分析计算结果见表15.

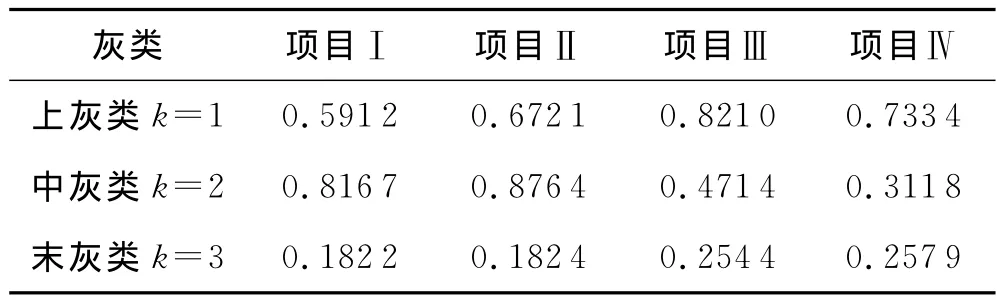
表15 聚类分析结果表

根据最大隶属度原则，项目i的灰类k为：k∈max｛ξk，j｜k＝1，2，3｝，因此项目Ⅲ属于上灰类，项目Ⅳ属于上灰类，项目Ⅰ属于中灰类，项目Ⅱ属于中灰类.即项目Ⅲ、项目Ⅳ应该投标，项目Ⅰ、项目Ⅱ可以投标.如项目Ⅲ和Ⅳ只能选择一个项目投标时，由于项目Ⅲ上灰类的隶属度／中灰类的隶属度＝0.821 0／0.471 4＝1.741 6；项目Ⅳ上灰类的隶属度／中灰类的隶属度＝0.733 4／0.311 8＝2.352 1；因此重点投标项目应该考虑项目Ⅳ.而工程实践中，企业选择的重点投标项目Ⅱ属于中灰类仅为可以投标项目，应为非重点选择的投标项目，应该在只有项目Ⅲ、项目Ⅳ都难以中标且施工企业业务较少、人员设备富余情况才考虑对项目Ⅱ投标.

4 结 语

投标项目优选决策是一种系统复杂的综合评价体系.一方面，考虑的因素很多，指标间又划分为不同的层次.另一方面，投标时部分信息已知，部分信息未知，具有灰色性.灰色聚类分析是一种既考虑了层次性，又考虑了灰色性的理论分析方法.在地质灾害防治工程投标项目优选决策中，根据地质灾害防治工程的具体特点，通过综合分析地质灾害防治工程投标影响因素，运用灰色聚类分析法进行投标项目优选决策是一种非常适用的理论方法.本文研究运用灰色聚类分析法进行地质灾害防治工程投标项目优选决策，建立了地质灾害防治工程灰色聚类分析的模型，并采用地质灾害防治工程投标实例对其进行了灰色聚类分析计算、验证，通过计算得出了投标项目优选决策的结果.灰色聚类分析法是一种科学的投标项目优选理论方法，该方法较单纯的层次分析简捷、直观，同时也不需要大量的样本进行统计分析.采用该方法快捷、方便，可以避免施工企业凭主观臆断优选投标项目的盲目性，提高企业的决策水平.

［1］ 万 俊，邓蓉晖.工程施工招投标中业主风险的分析与防范［J］.建筑经济，2001（3）：34－37.

［2］ 叶碎高.模糊分析法在国际工程投标决策中的应用［D］.大连：大连理工大学，2000.

［3］ 史永红.模糊综合评判法在建设工程投标决策中的应用［J］.价值工程，2012（32）：95－96.

［4］ 王莲芬，许树柏.层次分析引论［M］.北京：中国人民大学出版社，1989.

［5］ 杨 华.决策树分析法在企业投资决策风险分析中的运用［J］.福建教育学院学报，2009（5）：47－50.

［6］ 邓聚龙.灰色理论基础［M］.武汉：华中科技大学出版社，2002.

［7］ 刘丁慧，林和平，姜春燕，等.灰聚类分析及其应用研究［J］.吉林大学学报，2007（4）：412－417.

［8］ 李明凉.灰色关联度新判别准则及其计算公式［J］.系统工程，1998（1）：68－70.