对三峡库区某滑坡位移响应规律研究

杨巧佳 易庆林 胡大儒 赵能浩

（1.三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；2.三峡大学 湖北省地质灾害防治工程技术研究中心，湖北 宜昌 443002；3.中国电建集团 贵阳勘测设计研究院，贵阳 550081）

水库型滑坡变形通常受库水和降雨的综合作用.库水对滑坡的影响规律性较强，其作用是持续的，三峡库区大部分涉水滑坡的变形均受控于库水位的涨落.库水位变化幅度可人为控制，因此，在掌握了库水位对滑坡变形的作用规律之后，可极大地降低滑坡灾害带来的损失.降雨对边坡的影响有范围广、突发性强、可控性差等特点：任何地区只要有降雨，就有可能发生滑坡；持续降雨、突发暴雨、间歇性降雨均可成为滑坡灾害的诱因；由于降雨的强度、历时均无法准确预知，因此，通常降雨诱导的滑坡灾害只可被动避让，很难通过控制降雨量的多少来主动阻止或减缓灾害的发生.

滑坡在库水位及降雨作用下变形的时域规律研究是目前国内外的热点及难点课题，众多专家学者均做了各方面的尝试并提出了很多理论方法，对解决滑坡变形的时间预测预报问题有重要的意义.现阶段常见的滑坡变形时间规律预测理论有：斋藤模型、福囿模型、Verhulst模型、非线性动力学模型、Pearl预报模型［1－4］等.但由于滑坡系统的复杂性及各理论的局限性，相关研究仍不能满足工程实践的需要.目前对水库型滑坡变形的周期效应及滞后效应还没有系统完善的研究方法，通常只限于定性分析.本文在滑坡地表位移长期监测资料的基础上（每日一测），提出利用离散谱分析法研究在库水位及降雨作用下滑坡变形的周期效应，利用回归分析定量研究滑坡变形的滞后效应，并用极限平衡法计算库水位一个完整的下降周期内，不同降速方案下滑坡稳定性的变化规律，为滑坡变形的时域规律提供一种可行的研究思路.

1 滑坡概况

该滑坡属逆向古滑坡，前缘临江，地形总体陡缓相间，南北纵长约800m，东西宽约700m，面积约55×104m2，平均厚约50m，总体积约2 890×104m3.滑坡东侧中前部为主滑区，面积约35×104m2，总体积约1 575×104m3.滑坡平面图见图1.

滑体物质主要为崩坡积碎块石土，呈紫红色夹杂灰褐色或黄褐色.不同部位土石比差异较大，坡体下部以可塑状粉质粘土为主，土质结构稍密至密实；坡体上部以碎块石为主，由砂岩、泥岩、泥灰岩组成，呈棱角至次棱角状，直径一般为1～15cm.

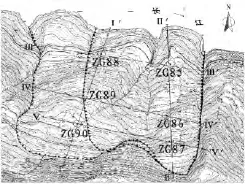
图1 滑坡及监测点布置平面图

滑坡东侧滑带为堆积层与基岩接触带，滑带土主要成分为粉质粘土，含碎石角砾，呈黄褐色、青灰色或紫红色，厚0.6～1.0m.西侧发育两层滑带，浅层滑带位于坡积层中，厚约1.0～1.2m，滑带物质为角砾土，褐黄色、黄绿色.深层滑带为堆积层与基岩接触带，主要成分为粉质粘土，内含角砾，厚约1.1～1.7 m，褐黄色、紫红色.

滑床基岩地质时代为三迭系中统巴东组，由一套紫红色、灰绿色中厚层状粉砂岩夹泥岩，以及灰、浅灰色中厚层状泥灰岩组成，岩层产状倾向135～205°，倾角10～35°，部分岩体中节理裂隙较发育.

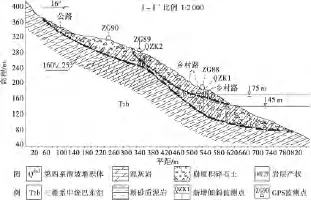
图2 滑坡Ⅰ－Ⅰ′剖面图

图3 滑坡Ⅱ－Ⅱ′剖面图

2 滑坡变形的时域规律分析

绘制滑坡累计位移、库水位、降雨量关系曲线（200504～201209）如图4所示.据图4可知，当库水位上升或维持稳定时，位移曲线呈现均匀缓慢增长趋势，当库水位下降时，位移曲线则呈现快速上升趋势；降雨量与累计位移呈正相关，每年6～8月为降雨高峰期，同时，每年1～6月为库水位下降期，两因素叠加作用下，位移曲线呈现台阶状陡增趋势，此时滑坡稳定性达到最低.每年9月～次年3月主滑区地表位移变化平缓，4～8月出现加速变形，监测期内位移量累计为1 564.6～4 523.8mm，方向354～24°，即指向长江.滑坡中后部为牵引区，变形量相对较小，基本呈线性增长，监测期内位移量累计为287.6～686mm，方向为354～24°，处于缓慢蠕动变形阶段.

图4 滑坡累计位移、库水位、降雨量关系曲线

由此可见，滑坡地表累计位移随库水位及降雨的变化呈现出一定的周期性，同时位移响应较库水位、降雨的变化相对滞后.本节将分别运用离散谱分析、回归分析定量研究上述周期效应及滞后效应规律.同时，由于滑坡累计位移在每年库水位下降时加速增长，因此将研究不同库水位速率对滑坡稳定性的影响.

2.1 滑坡变形的周期效应分析

离散谱分析也称谐波分析法，是利用傅立叶级数将时间序列展开成离散谱的分析过程.滑坡位移时间序列的周期分量可用一组正弦函数来表示，因此可用傅立叶级数将其在一定区间上展开，然后通过波参数之间的函数关系分析确定该序列的周期或显著性周期.

对于一个位移时间序列xt（t＝1，2，…，n），进行傅立叶级数展开［5］有

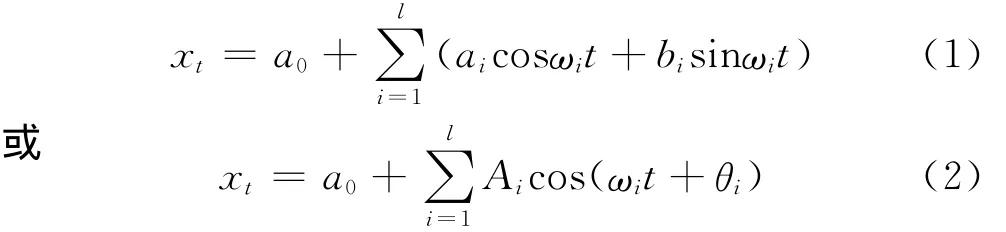
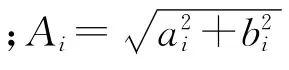
则序列xi的第i个谐波为

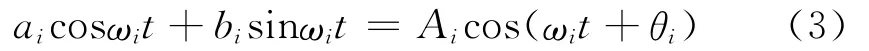
其频谱值为

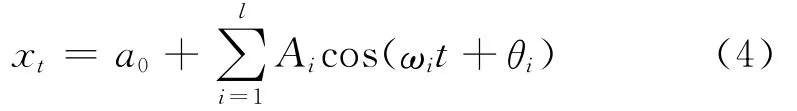
显著性检验：在显著性水平为0.05时，位移时间序列xt的振幅为A0.05，因此有

社会学解释。随着日常工作和社会环境的不断作用下，高校基层行政管理人员对自身职业认同的不断调整和变化，有了新的认识和态度。在建立职业认同感的过程中，有些行政人员对自身的职业产生了一系列疑惑。有学者认为能够从角色角度作为出发点研究职业倦怠现象，并认为角色间冲突、角色内部冲突和角色模糊是导致职业倦怠的主要原因。

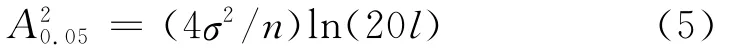
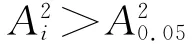
对监测点ZG88的位移曲线进行离散谱分析可得振幅谱曲线，如图5所示.最大峰谱对应的周期值为12，可认为该位移时间序列的周期为12个月.

图5 离散谱分析振幅谱曲线

2.2 滑坡变形的滞后效应分析

2.2.1 库水位下降时滑坡变形滞后性规律

选取20120620～20131020期间降雨量为0的时段，对监测点ZG85、ZG88地表位移增速、库水位降速v1、库水位降速持续时间t1、变形滞后时间T1进行统计，结果见表1.

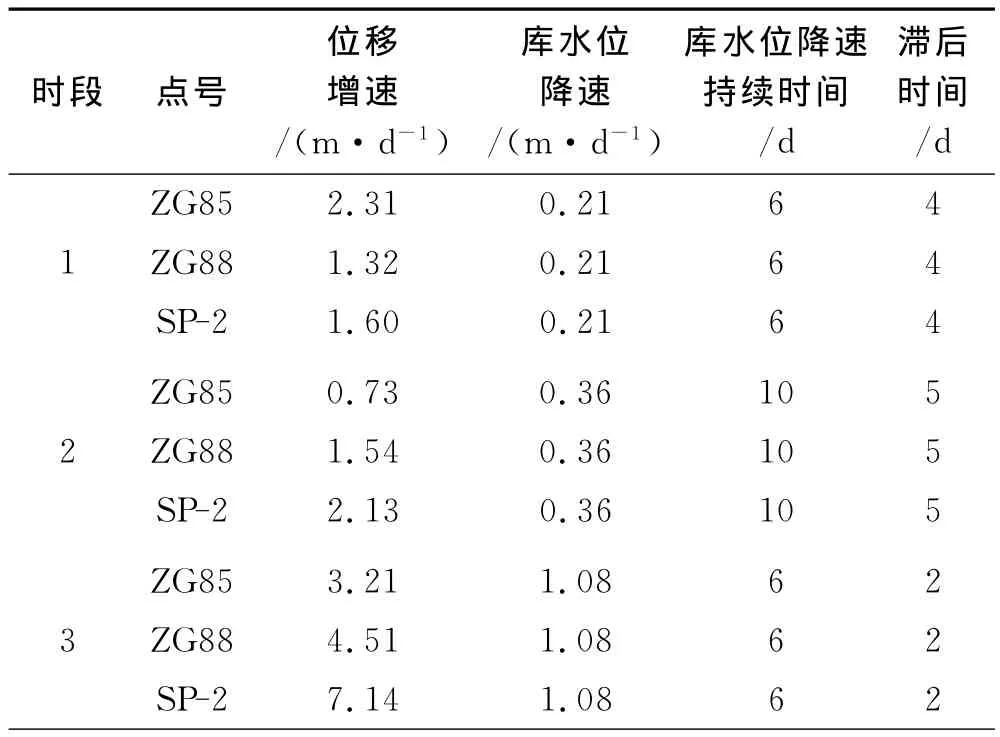
表1 不同库水位降速下滑坡变形滞后时间统计

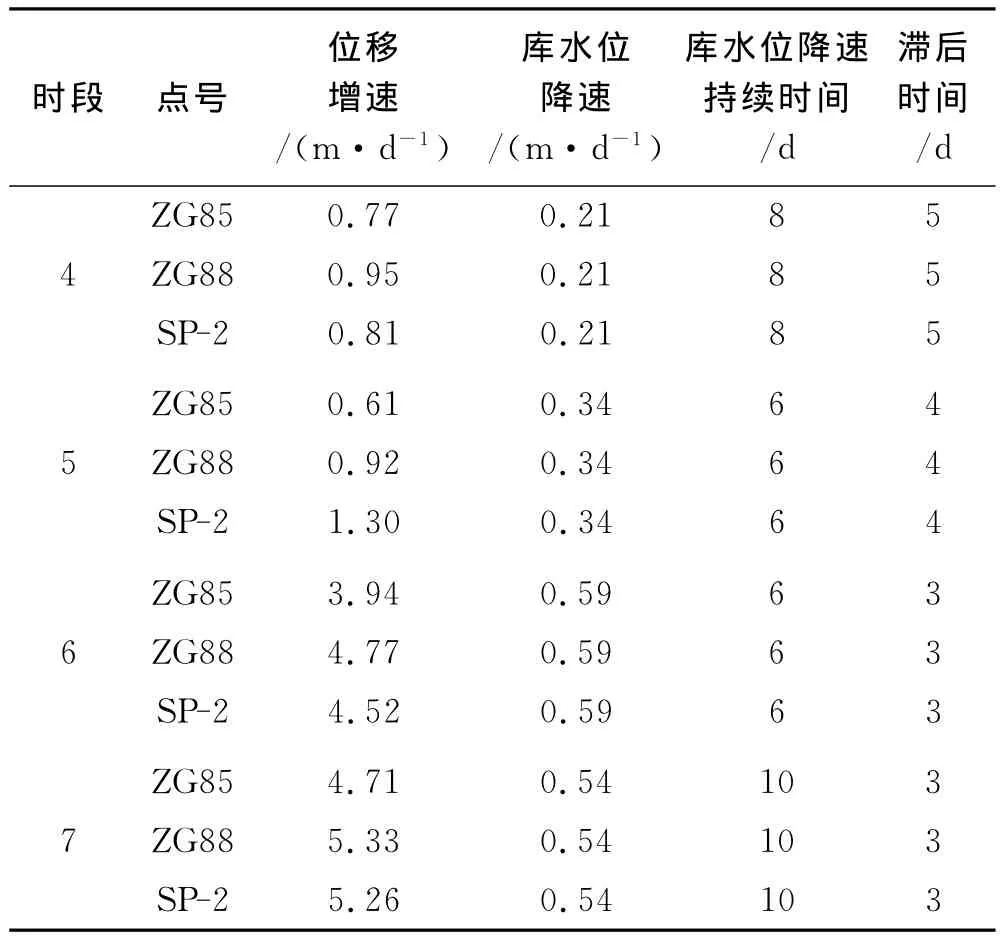
续表1 不同库水位降速下滑坡变形滞后时间统计

表2 相关系数信息

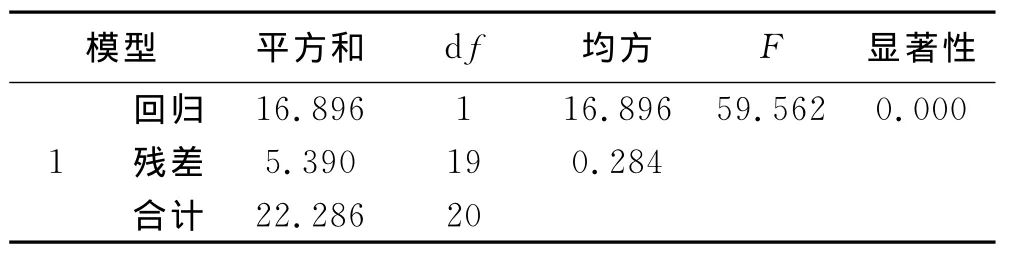
表3 方差分析及检验

表4 回归系数及检验

表2～4分别给出了回归模型的相关系数信息、回归拟合的方差分析结果、回归系数估计值.表中相关性系数R值达到0.871，调整的R2达到0.745，说明拟合优度良好.显著性检验时只有v1能满足要求，其他各自变量均被剔除，最终建立T1－v1回归模型为

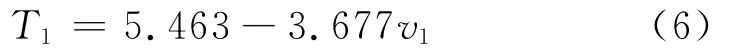
2.2.2 库水位下降叠加降雨时滑坡变形滞后性规律

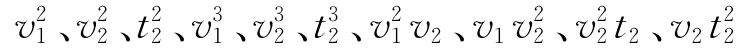
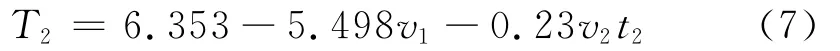
据上式可知，当库水位下降伴随降雨作用时，T2与v1及v2t2（降雨量）均成线性关系.由两自变量的系数可知，当库水位降速或降雨量增大时，滞后时间将减小，但v2t2系数的绝对值比v1的小一个数量级，说明库水位降速占主导作用.

需要指出的是，滑坡滞后期的精度与地表位移监测的频率有关，监测频率达到每天一次，则滞后期可精确到天，监测频率达到每小时一次，滞后期则可精确到小时.

2.3 库水位单个下降周期内滑坡稳定性分析

由前文分析可知，库水位下降是导致该滑坡加速变形的主要影响因素，因此，本节将模拟单个库水位下降周期内，不同的库水位下降方式及降速对滑坡稳定性的影响，相关理论见参考文献［9－12］.在滑坡数值计算中，滑体、滑带及滑床的计算参数是通过室内试验、反算分析、工程类比等技术手段确定的，详见表5.具体计算模型与网格划分结果如图6所示，整个计算域剖分了1 284个四节点单元，共计1 338节点.

表5 滑坡岩土体力学参数表

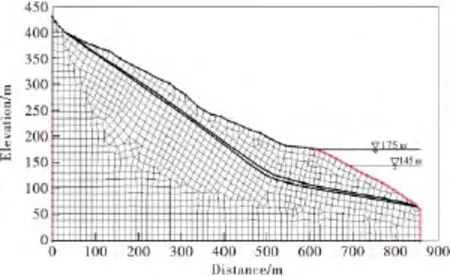
图6 滑坡计算模型建立及网格划分

因三峡工程防洪发电的双重需要，库水位在每年1月初开始下降，至6月10日前必须降至145m，以腾出库容迎接洪峰，因此库水位下降的起始时间、终止时间、水位下降幅度均已确定时，不同的库水位下降工况，对滑坡稳定性的影响也不同.本节将在库水位实际下降工况的基础上，拟定3类（5种）可能的工况，以讨论不同水位下降方式对滑坡稳定的影响.

1）工况1（实际下降工况）：库水位以0.12m／d的速率由175m降至163m，以0.26m／d的速率由163 m降至145m.

2）工况2（匀速下降工况）：库水位以0.18m／d的速率由175m降至145m.

3）工况3（先缓降，后快降）.①以0.12m／d的速率由175m降至163m，以0.36m／d的速率由163m降至145m.②以0.13m／d的速率由175m降至163 m，以0.23m／d的速率由163m降至145m.

4）工况4（先快降，后缓降）.①以0.25m／d的速率由175m降至163m，以0.15m／d的速率由163m降至145m.②以0.3m／d的速率由175m降至163 m，以0.14m／d的速率由163m降至145m.

对以上5种工况进行数值模拟分析，得到库水位以不同的速率由175m降至145m（历时170d）时，滑坡安全系数随时间的变化关系曲线，如图7所示.

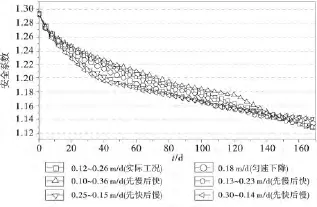
图7 库水位正常下降阶段不同工况下安全系数曲线

由于库水位每年1月初开始下降，6月10之前必须降到145m，历时170d左右，由于滑坡稳定性系数受库水位升降变化较大，其中最小稳定系数对滑坡失稳与否起决定性作用，因此通过以上几种工况的最小稳定性系数来判断其优劣.据图6可知：1）库水位下降，滑坡安全系数减小，库水位降速越大安全系数降速也越大.2）库水位先快速下降后缓慢下降时（工况4），水位到145m之后，滑坡安全系数较其他工况大，但工况4的2种方案中，方案1库水位快速下降阶段（以0.25m／d的速率下降）安全系数较方案2库水位快速下降阶段（以0.30m／d的速率下降）大.因此工况4的第1种方案更优.

3 结 论

1）运用离散谱分析求得在库水位及降雨作用下，滑坡变形的周期为12个月，与实际情况相吻合.运用回归分析求得滑坡变形滞后期与库水位降速的相关模型为T1＝5.463－3.677v1，与库水位降速及降雨强度的相关模型为T2＝6.353－5.498v1－0.23v2t2，且库水位降速对变形滞后期的影响占主导作用.

2）运用极限平衡法计算可知，库水位降速与滑坡稳定性呈负相关，库水位下降历时、降幅一定时，采用先快降后缓降同时避免陡升陡降的库水位调度方案，可获得较高的安全系数.

［1］ 易庆林，胡大儒，代天凡，等.基于小波分析的滑坡变形规律研究［J］.南水北调与水利科技，2013，11（5）：91－94.

［2］ 胡大儒，易庆林，李 平，等.三峡库区某滑坡稳定性时域分级评价［J］.地下空间与工程学报，2014，10（2）：480－485.

［3］ 张奇华，丁秀丽，邬爱清.滑坡变形预测与失稳预报问题的几点讨论［J］.中国地质灾害与防治学报，2005，16（2）：116－120.

［4］ 彭 令，牛瑞卿，三峡库区白家包滑坡变形特征与影响因素分析［J］.中国地质灾害与防治学报，2011，22（4）：1－7.

［5］ Elias M.Stein，Rami Shakarchi.Fourier Analysis：An Introduction［M］.Princeton University Press，2003.

［6］ 邱祥波，李术才，李树忱.三维地应力回归分析方法与工程应用［J］.岩石力学与工程学报，2003，22（10）：1613－1617.

［7］ 付 勇，汪立今，柴凤梅，等.多元线性回归和逐步回归分析在白石泉Cu－Ni硫化物矿床研究中的应用［J］.地学前缘，2009，16（1）：373－380.

［8］ 王志强，柴寿喜，仲晓梅，等.多元逐步回归分析应用于固化土强度与微结构参数相关性评价［J］.岩土力学，2007，28（8）：1650－1654.

［9］ 许 强，汤明高，徐开祥，等.滑坡时空演化规律及预警预报研究［J］.岩石力学与工程学报，2008，27（6）：1104－1112.

［10］陈祖煜.土质边坡稳定分析［M］.北京：中国水利水电出版社，2003.

［11］Morgenstern N R，Priee V E.Analysis of Stability of General Slip Surfaces［J］.Geotechnique，1965，15（1）：79－93.

［12］李广信.高等土力学［M］.北京：清华大学出版社，2004.