基于矩阵编码遗传算法的PCB生产线元件分配优化
2015-07-25李登桥
杜 轩 李登桥 朱 康
(三峡大学 机械与动力学院,湖北 宜昌 443002)
电子产品需求的日益增加,促进了印制电路板(Print Circuit Board,PCB)的大批量组装生产,连续生产线作为工业生产中一种典型的布置方式,在PCB组装生产过程中也得到了广泛的应用,即把组装过程中所用到的设备依照一定的工艺次序组合,用传送带串联成一条连续的生产线,所有PCB以相同的顺序通过生产线上的所有设备,完成元件组装.PCB在生产线上的组装时间是由生产线上所有设备中耗时最长的设备所决定,对PCB在不同设备上组装的元件进行分配优化,可实现各台设备间的负荷平衡,缩短PCB组装时间,此问题即为连续生产线上的元件分配问题.PCB组装生产线上的元件分配和PCB分配优化属于典型的组合优化问题,其计算复杂度高,也是一种NP-hard难题.
目前,针对PCB生产线元件分配问题的研究主要采用数学规划方法、启发式方法等.而遗传算法在求解组合优化问题中,具有全局性概率搜索的特点,在搜索过程中能自动获取和积累相关搜索空间的知识,并结合自适应的控制搜索过程,因此在这一类问题的优化计算中表现出了较大的优势.文献[1]中Ho W和Ji P,建立了连续PCB组装生产线上元件分配优化模型,然后应用传统遗传算法对问题进行求解,从而解决了连续生产线上元件分配和多条生产线上的PCB分配优化问题.文献[2]基于多台不同类型典型表面贴装设备所组装成的印制电路板组装生产线,针对上述组装机及组装流水线的调度问题,建立相应的集成调度优化模型,从而为后续研究电子产品制造企业生产线调度问题的智能优化算法提供了理论依据和技术支持.文献[3]中针对表面组装生产线负荷平衡问题,建立了以最小化最大单机贴装时间为目标函数的整数规划模型,并采用传统的伞布式搜索方法对模型进行优化求解,最后通过实验仿真得到优化结果,表明了此算法在求解此类问题的有效性.文献[4]提出了流水线调度优化问题,进而采用传统遗传算法(TGA)对问题进行求解,同时应用实际生产数据进行试验,证明此方法的优越性.
目前,针对PCB组装生产线上元件分配优化问题的研究已经取得了部分的研究成果,但是,还有一定的优化提升空间,主要表现在以下几个方面:1)部分研究所建立的优化模型不能够很好反应企业实际情况,导致所求的结果不能直接应用于实际生产;2)一般的研究在进行模型求解时所采用的方法有一定的局限性,而且求解效率较低,求解结果表述不明了,在诸多方面还有改善和提升空间[5].基于上述的分析和已有的研究成果,本文设计了一种新的基于矩阵编码方式,提出了结合最小元素法的方法,高效实现了种群初始化操作;采用两点交叉的方式进行交叉操作,从而提高了种群多样性;采用改进的局部变异法,再次结合最小元素法实现了变异操作;最终,通过算法求解实现了PCB组装连续生产线上的元件分配优化问题,并通过实例仿真验证,表明了此方法的有效性和优越性.
1 PCB生产线元件分配问题描述及优化模型建立
1.1 PCB生产线元件分配问题描述
考虑一种PCB在一条连续生产线上组装,由于组成生产线的设备性能差异,不同的设备组装同一类型的元件所用的时间是不一样的,即使是同一设备在组装不同元件时所需要的时间也不同,甚至有些设备对某些特定的元件根本无法完成组装.因此需要将PCB上的元件合理地分配到不同的组装设备上,平衡各台设备上的工作负荷,以减少PCB的组装时间[6].如图1中所示即为n中不同类型的元件在一条生产线上m个不同设备之间进行分配的模型.

图1 元件在设备间分配的分配模型
1.2 元件分配优化模型
假设PCB上有L种不同类型的元件,在M台设备上进行组装,第i种类型的元件在设备k上组装的数量为Cki,第i种类型的元件在设备k上组装所需的时间为tki;组装设备的调整时间为sk.元件分配优化问题的数学模型可描述如下:

式中,i为元件类型的编号,i=1,2,…,L;k为组装设备的编号,k=1,2,…,M;cki为元件类型i在设备k上组装的数量;sk为组装设备k的调整时间;tki为元件类型i在设备k上的组装时间;N为PCB上组装元件的数量.
目标函数式是使生产线上耗时最长设备的组装时间最小化.
2 遗传算法求解与实现
2.1 染色体编码
编码方式的选择是运用遗传算法解决问题的关键.对于元件分配优化问题,如果采用传统的二进制字符串编码方式,当元件的类型及设备数量增加时,染色体的长度会急剧增加,导致算法实现时间复杂度和空间复杂度增加,影响求解效率[4].根据元件分配问题自身的特点,可采用矩阵形式的编码方式,一条染色体的编码为

式中,行表示生产线上的设备,列表示PCB上的元件类型,矩阵的元素xij表示第j种类型的原价在设备i上组装的数量.一条染色体的结构实际上就描述了元件分配问题的一种方案.因此采用矩阵编码有利于问题的求解.
2.2 种群初始化
如何保证产生的初始种群中的所有个体都能满足问题的约束条件式是初始种群产生的难点所在.对于整数约束,只需要保证染色体中每个元素变量都是大于0的整数即可.对于如何保证元件数量约束存在一定的难度.本文中将采用最小元素法,即找出运价表中最小的元素,在运量表内对应的格填入允许取得的最大数,若某行(列)的产量(销量)已满足,则把运价表中该运价所在行(列)划去;找出未划去的运价中的最小数值,按此办法进行下去,直至得到一个基本可行解的方法[7].
通过问题的数学模型和解的表达形式,可以看出,此问题与运输问题很相似.对于产销平衡的运输问题的可行解是很容易被确定的,且产销平衡的运输问题一定存在有限最优解.求解运输问题的常用方法是表上作业法,虽然此方法的求解效率很低,有可能得不到问题的最优解,但是可以借鉴其中的最小元素法的思想来产生满足约束条件的初始种群[8].
对比元件分配问题的数学模型与产销平衡运输问题的数学模型后可以发现,两种问题的最大不同点在于前者比后者少了一个约束条件,即对每台设备要组装的原价类型数量没有限制.但是由于问题的实际意义可以看出,这一约束条件是隐含存在的,为了使元件得以顺利的组装,必须使所有的设备组装元件的个数之和等于元件的总个数.此处假设每台设备上组装元件的个数为bi(i=1,2,…,m)且bi≥0,上述的描述可以用下式来表示:

增加一个约束条件:

此时,元件分配问题就转化为了“产销平衡的运输问题”,初始化种群按照以下步骤来生成:
1)随机分配给bi一个整数,并且使得bi满足元件的数量约束条件.
2)从集合δ=(1,2,…,m×n)中随机选择一个数k.
3)由下式计算k在编码矩阵中所对应的行i和列j:
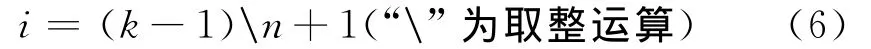
j= (k-1)mod(n)+1(“mod”为取余运算)(7)
4)确定变量xij的值.

5)由下式更新bi和ci的值,并从集合δ中删除元素k.

如果bi<0,则将其置为0,cj也做类似操作.
6)重复步骤2)~5),直到集合δ为空,这样就产生了问题的一个可行解,即一条染色体.
对上述步骤1)~6)重复操作执行多次,便可得到问题的初始种群.可以看出,采用这种方法所得到的个体全部满足问题的约束条件,即为问题的可行解,进而充分保证了后续搜索空间的有效性.
2.3 适应度函数及选择
适应度函数用来对个体的优劣程度进行评价,这里采用个体时间作为个体的适应度,对其进行评价[9].
本文的选择操作将采用二元锦标赛选择方法和最优保存策略相结合的方法来进行个体的选择,采用二元锦标赛选择方法选择进行交叉变异的个体,交叉变异所产生的新个体和父代种群中的个体同时采用最优选择策略,用适应度高的个体产生下一代种群,且种群的数量要保持不变.
2.4 交叉与变异
交叉操作即对父代的两个染色体在指定的基因位进行交叉运算,以产生新个体.交叉概率Pc控制着交叉算子的应用频率,在种群大小为M的群体中,需要对pc×m个染色体进行交叉操作,交叉概率越高,群体中新结构的引入越快,已获得的优良基因基因机构的丢失速度也相应越高,而交叉概率太低则可能导致搜索阻滞[10].此处采用线性递减函数产生交叉率Pc,假设第一代与最后一代的Pc分别为Pc1和Pcn,迭代终止次数为N,则第i代的交叉概率Pci为

为了保证交叉之后的个体满足最初的约束条件,基于矩阵编码的方式需保证每列的和满足题设中的要求.即在进行交叉时只能保证对应列进行交叉.采用这种交叉方式就可以保证个体始终是满足约束条件的有效个体,从而有效保证了遗传操作的正常进行.
变异即改变染色体上的一个或一些基因座上的基因值为其它的基因,以产生新的个体.对采用二进制编码的染色体只需对指定的基因位进行0和1之间的转换即可.而对于此处采用矩阵形式表示的染色体,为了使变异后的个体也是问题的可行解,则不能进行简单的基因位的转换,因此,变异采用以下的方法进行.
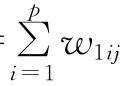
3 算法实现及优化实例
3.1 实例分析
采用实际生产中的实例进行例证分析,以文献[1]中所用的元件和设备信息为例,计算元件的分配问题.具体的数据如图2所示,图2中共有7种不同类型的贴片元件和3台不同的贴片设备,各种类型的元件个数Cj和设备调整时间Si如图所示.图2中的右上角的数据表示相应的设备组装相应的元件所需的时间(单位0.1s),符号∞表示相应的设备不能对相应的元件进行组装[11],在算法实现时,可以将∞符号赋值为一个较大的实数即可,这样在进行元件分配时,如果分配给此种设备的相应元件类型时,此个体的适应度就会较高,因此在遗传操作过程中就会逐渐被淘汰.

图2 实例数据图
3.2 算法实现步骤
采用改进的遗传算法,其具体实现步骤:
1)设置遗传算法(GA)参数.主要包括种群大小(Psize)、遗传代数(Count)、交叉概率(Pc)和变异概率(Pm).
2)种群初始化.根据染色体的编码规则和要求,生成Psize个二维十进制分段的染色体,形成初始化种群.
3)计算适应度.根据适应度评价函数,计算种群个体的适应度值.
4)适应度值比较.采用二元锦标赛选择方法,保留个体中适应度值较大的个体,进行下一步的交叉和变异操作.
5)交叉操作.采用改进的交叉方法生成新种群.
6)变异操作.结合最小元素法,应用改进的局部变异以及自适应的变异率方法进行变异操作.
7)通过遗传操作之后保留每代中的最优个体.
8)重复步骤4)~8),直到完成所设定的迭代次数,得到最优个体以及最大适应度值.
3.3 求解结果及分析
本文算法使用Matlab编程,采用GA算法对实例数据进行求解,测试实际生产线的数据.实验对象为一条连续的PCB组装生产线,共3台组装设备,7种不同的元件类型,每种不同类型的元件都有不同的数量,不同类型组装设备在组装不同类型元件时其速度也各不相同,每台组装设备的调整时间也不同.
在算法的实现过程中采用的主要遗传操作参数为:初始种群Psize=100,遗传代数Count=50,初始交叉概率Pc1=0.8,终止交叉概率Pcn=0.6,变异概率Pm=0.2,采用改进的遗传算法对图2中的工程实际问题进行求解,多次运行之后取平均值,得到算法收敛图如图3所示.

图3 PCB组装生产线元件分配优化收敛图
最终得到的最优化结果为99.5s.元件分配结果为
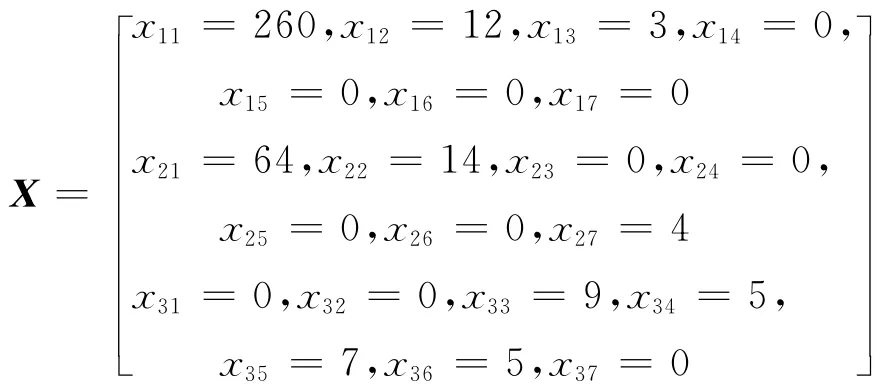
4 结 论
本文主要分析了PCB组装连续生产线上的元件分配优化问题,并建立了此问题的优化数学模型.详细介绍了元件分配优化问题的改进遗传算法求解过程,并通过实例验证了算法的有效性.基于矩阵编码的改进遗传算法,在求解类似元件分配组合优化问题中表现出了较好的寻优能力,同时此方法也可以应用于PCB分配优化问题求解,对此方法进行有效的拓展使用,可以很好地解决很多工程实际问题,具有一定的应用研究价值.
[1] Ho W,Ji P.Optimal Production Planning for PCB Assembly[M].London:Springer,2007.
[2] 靳志宏.印刷电路板组装生产线调度优化问题建模[J].中国管理科学,2008,16:122-127.
[3] 刘海明,袁 鹏,罗家祥,等.表面组装生产线的负荷平衡优化算法研究[C].Proceedings of the 32nd Chinese Control Conference,July 26-28,2013,Xi'an,China.2585-2590.
[4] 郭妹娟,靳志宏.表面组装技术生产线贴片机负荷均衡优化[J].计算机集成制造系统,2009,15(4):817-822.
[5] 王 君,罗家祥,胡跃明.基于混合搜索算法的贴片机贴装过程优化[J].计算机测量与控制,2011,19(3):603-605.
[6] 路军营,朱光宇.基于灰熵关联分析的表面贴装多目标优化[J].计算机集成制造系统,2013,19(4):766-772.
[7] 张 屹,万兴余,郑小东,等.基于改进元胞多目标遗传算法的机床主轴优化[J].计算机工程与应用,2013(7):31.
[8] 李 超.装备制造企业物流运输成本的控制研究[D].西安:西安科技大学,2011.
[9] 王 君,罗家祥,胡跃明.基于改进蚁群算法的贴片机贴装过程优化[J].计算机工程,2011,37(14):256-258.
[10]曾又姣,金 烨.基于遗传算法的贴片机贴装顺序优化[J].计算机集成制造系统,2004,10(2):205-208.
[11]李军华,黎 明.元胞遗传算法的收敛性分析和收敛速度估计[J].模式识别与人工智能,2012,25(5):874-878.
