基于分形插值的ARIMA大坝预警模型

屠立峰 包腾飞 李月娇 赵 斌

（1.河海大学 水利水电学院，南京 210098；2.河海大学 水资源高效利用与工程安全国家工程研究中心，南京 210098；3.南京南瑞集团公司 国际公司，南京 210093）

大坝的变形、应力和作用荷载等观测资料均为典型的时间序列，故可通过过去的观测值来预估未来的观测值.对于非平稳的时间序列，差分自回归移动平均模型（ARIMA模型）具有良好的适应性，常作为经典的时间序列模型［1］.时间序列覆盖的历史越长，可靠性也就越高，但也越有可能包含缺失值，所以对该组数据进行分析时，预测和拟合数据与实际监测值会有较大的误差.对于缺失率较低的情况可用现有的数据进行分析，然而大量信息的丢弃会使数据分布产生偏斜而扭曲数据挖掘和数据分析，从而误导决策，为此需通过数据填补来解决.通过函数插值可以弥补时间序列存在缺失值而导致预测误差较大的弊端，然而传统的插值函数由于两端的插值区间易出现“龙格现象”而限制了在拟合和数据处理中的应用，基于此学者们提出了分形插值的方法.分形插值是基于分形几何学提出的迭代函数系统，分形几何学指出任何一个局部都与整体自相似或统计自相似，因此可将已知数据插值成具有自相似结构的曲线和曲面.研究表明，分形插值与传统的插值方法相比具有更高的精度和适应性［2］.考虑到大坝监测数据间复杂的动态性和非线性的特点，本文为弥补ARIMA模型对含有时间缺失值的序列预测失准的弊端，对缺失的时间序列进行分形插值，以提高模型的预测精度.

1 分形插值

1.1 分形插值原理

一个数据集合是形如｛（xi，yi）∈R2｜i＝0，1，2，…，N｝的点集，其中

插值函数对应的这组数据是一个连续函数f：［x0，xN］→R，如

点（xi，yi）∈R2称为插值点，f（x）被称为插值函数.

传统的插值函数一般由初等函数的一组基函数线性表观的，相邻的插值点只可用直线或光滑的弧线衔接，却得不到两点之间的部分情况.分形插值函数是由一类特殊的仿射变换生成的，它可以得到两个相邻的信息点之间的局部变化，它为描述了一个不规则、随机曲线拟合的实验数据提供了强大的工具［3］.

1.2 分形插值方法

给定数据集｛（xi，yi）｜i＝0，1，2，…，N｝，构造迭代函数系统（IFS）｛R2；Wn，n＝1，2，…，N｝，其中Wn是具有如下型式的仿射变换：

并且

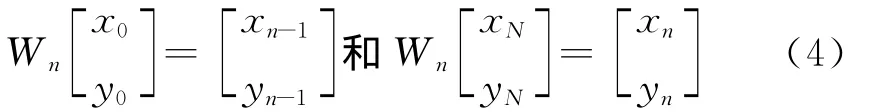
为了确保各小区间的不交迭，令式（3）中的bn＝0.式（4）具体可写为

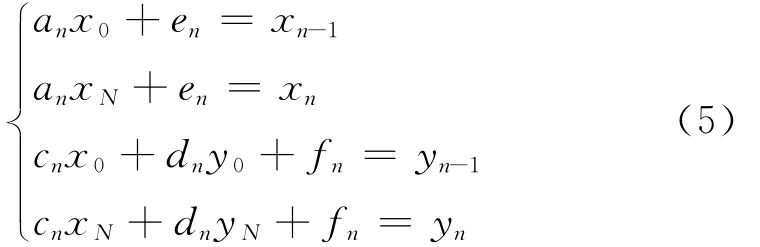
式（5）中有4个方程5个参数，所以其中一个是自由参数.在一般情况下，选择dn为自由参量，称为变换Wn的垂直比例因子.为保证IFS收敛，令｜dn｜＜1，解方程组（5），并令L＝xN－x0，则

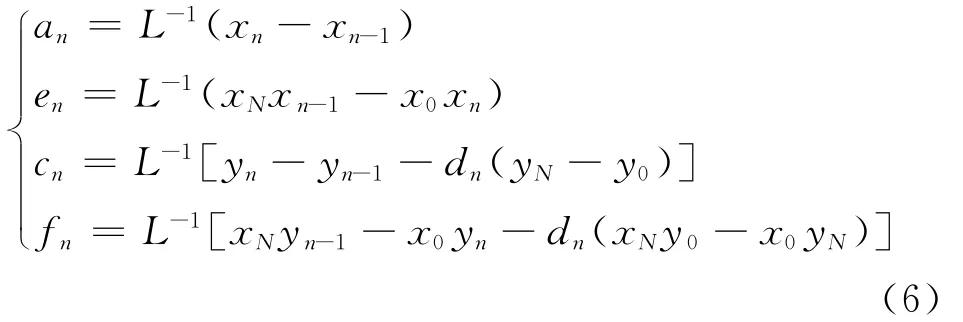
2 基于分形插值的ARIMA模型

2.1 ARIMA模型定义

ARIMA模型是指经过差分将非平稳的时间序列转化为平稳的时间序列，而后根据转化后得到的平稳时间序列创建ARIMA模型.该模型认为：系列数据随着时间的推移，预测形成随机序列，利用近似数学模型来描述这个随机序列，识别后的模型就能利用时间序列的过去值对未来进行预测［4］.

ARIMA（p，d，q）模型数学表达式如公式（7）所示：

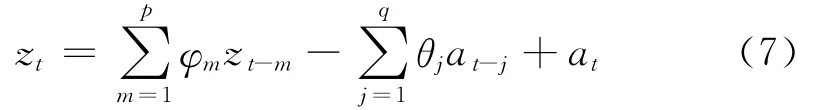
式中，φm（m＝1，2，…，p）是自回归模型的系数，θj（j＝1，2，…，q）均滑动模型的系数，p为自回归阶数，q为滑动平均部分的阶数，at白噪声序列.

2.2 基于分形插值的ARIMA模型建模流程

大坝安全监测数据一般为非平稳时间序列，模型建立步骤如下：

1）判断给定的时间序列是否含有缺失值，若为有缺损值的时间序列需对该组数据进行分形插值，得到数据填补后的序列样本.反之则跳转至2）.

2）进行平稳性检验得到参数d，即差分阶数.平稳性检验常用的方法有两种：一种是图检验法，另一种是构造检验统计量进行假设检验的方法［5］.图检验法是依据自相关图的平稳性检验方法，因其简便和运用广泛的特点，采用该方法将大坝安全监测量转化为平稳的时间序列.

3）确定模型类型后，使用赤池信息量准则（AIC）或贝叶斯信息准则（BIC）判断模型的p、q值.由于BIC准则比AIC准则具有更好的收敛性［6］，故本文采用BIC准则计算模型的p、q值.其数学表达式为

式中，k为参数的数量，n为观察数.

式（8）表明BIC准则主要有两部分组成，一是参数的数量，随着阶数的增大而增大；二是模型的拟合情况［7］.增加自由参数的数目可提高了拟合的优良性，BIC鼓励数据拟合的优良性，但是尽量避免出现过度拟合的情况［8］.所以选择BIC值最小组对应的p、q值.

第4步：在上述模型识别的基础上，采用极大似然估计或最小二乘估计法进行参数估计.

第5步：进行假设检验，诊断at是否为白噪声序列.

第6步：根据建立好的ARIMA模型对大坝变形参数进行拟合和预测.

3 工程应用实例

小湾水电站为混凝土双曲拱坝，坝顶高程1 245 m，最大坝高293.5m，总装机容量420万kW.以小湾坝顶20120701～20120919观测得到的数据为例，其中 20120706～20120710，20120726～20120730，20120816～20120825观测数据缺失.首先利用Matlab数学软件对缺失的数据进行分形插值，再利用SPSS软件对得到的连续时间序列建立ARIMA模型进行拟合预测，最后与原始的ARIMA模型进行对比.本文采用小湾拱坝坝顶位移的原始观测值前70组进行拟合，后10组数据进行预测.

3.1 分形插值

通过Matlab数学软件对观测值中的缺失值进行分形插值，启动Matlab软件，在命令窗口中做如下操作：

通过计算可以得到20120706～20120710，20120726～20120730，20120816～20120825值插值后的位移值.表1为经过分形插值后的数据.

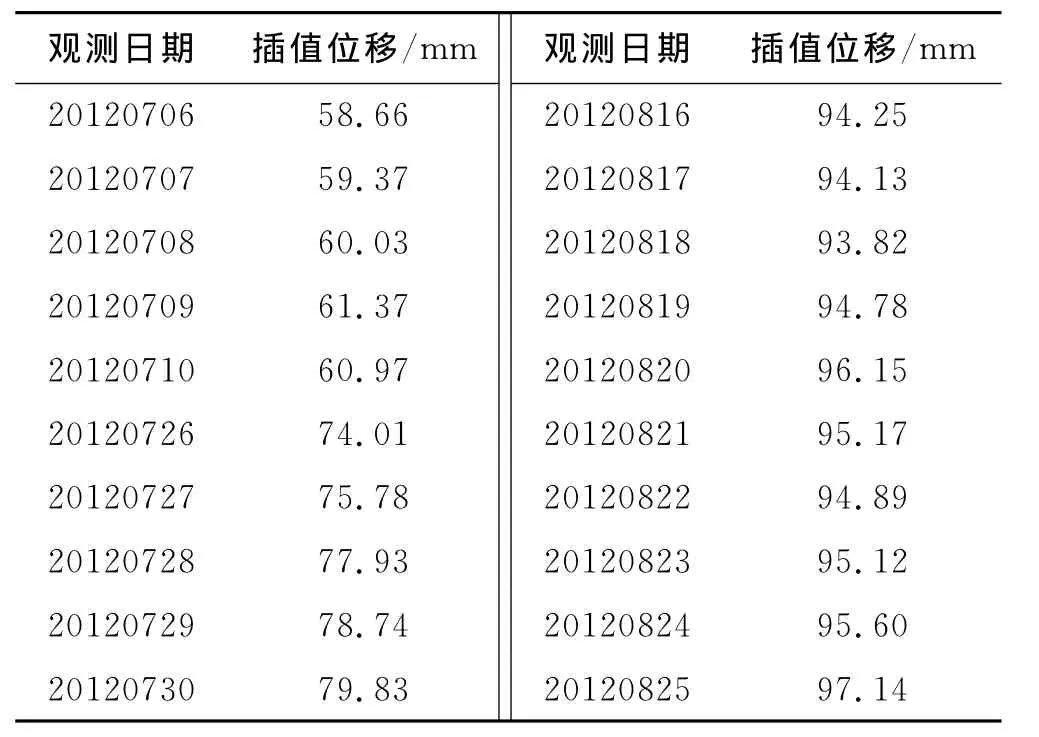
表1分形插值数据表

3.2 基于分形插值的ARIMA模型

通过差分将坝顶观测位移平稳化，下面利用图检验法分析序列的平稳性以确定模型的阶数.一阶差分后的自相关系数（ACF）和偏自相关系数（PACF）如图1所示.

图1 ACF（左）和PACF（右）系数图

由图1可看出，当滞后步数大于等于2时，自相关系数和偏自相关系数均落在置信区间内，因此可以认为经一阶差分后时间序列是平稳的.表2为从低阶到高阶不同的BIC值.

表2 ARIMA模型BIC准则值

由表2可知，ARIMA（1，1，3）模型对应的BIC值最小，故其相应的精度就越高.运用相同的方法对未经分形插值的时间序列建立ARIMA（0，1，1）模型，分别对原始监测数据进行拟合，并计算相应的误差，拟合结果见表3.

表3 两种模型的拟合值与相对误差

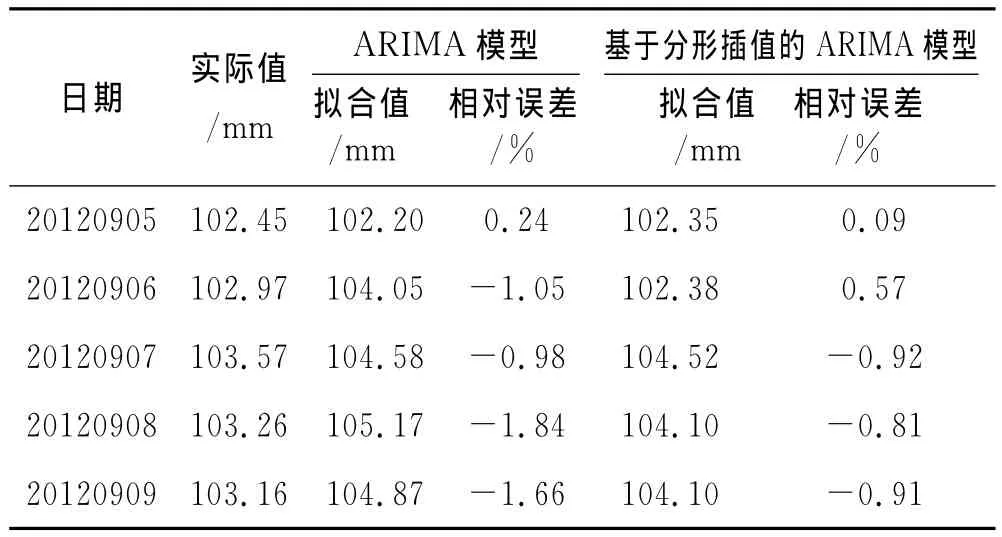
续表3 两种模型的拟合值与相对误差

由表3可看出，除个别观测日期外，基于分形插值的ARIMA模型的拟合值更接近于实测值，利用基于分形插值的ARIMA模型的相对误差小于原始的ARIMA模型.分别利用ARIMA模型和基于分形插值ARIMA模型对实测值展开预测，预测结果见表4.

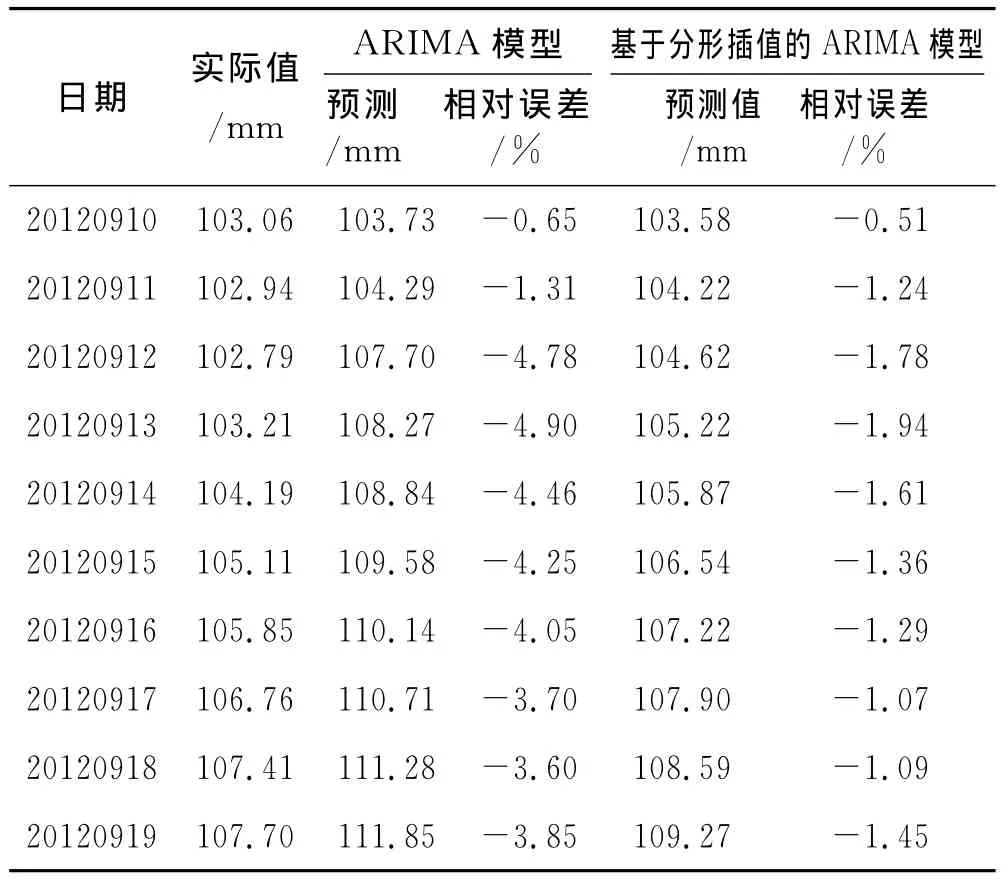
表4 两种模型的预测值与相对误差

由表4可看出，基于分形插值的ARIMA模型的预测值更接近于实测值，利用分形插值的ARIMA模型的相对误差都小于原始ARIMA模型的相对误差.

将表3～4计算所得两种模型的拟合数据和预测值与实测值进行比较，比较结果如图2所示.

图2 两种模型的拟合值与实测值的比较

通过表3～4以及图2可以得到，对于含有缺失值的时间序列，基于分形插值的ARIMA模型的预测值的平均相对误差由原先的3.56%降低至1.34%，表明该模型的预测精度显著提高.

4 结 论

1）在实际监测过程中，数据缺失是常见的现象，本文以小湾水电站坝顶位移预测为例，建立了基于分形插值的ARIMA模型，利用分形插值法对含有数据缺失的时间序列进行插值，从而建立ARIMA时间序列模型，得到坝顶位移预的拟合预测.计算结果表明，改进后的ARIMA模型的预测精度明显提高.

2）通过预测值和实际值比较发现，由于ARIMA模型对于单调数据处理的不足，易出现预测值单调迅速增长的现象，导致预测值均大于实测值.针对ARIMA模型的不足，近年来学者们已经陆续提出了基于ANN－ARIMA、GM－ARIMA等应用模型.基于此，对于含有一定数据缺失的时间序列可将分形插值与优化后的ARIMA模型相结合，进一步的提高预测精度，不失为一种新的研究方向.

［1］ 岳莉莉.基于时间序列分析的风速短期预测方法研究［D］.北京：华北电力大学，2012.

［2］ 李信富，李小凡.分形插值与拉格朗日插值的比较研究［J］.黑龙江大学自然科学学报，2008（3）：323－326，331.

［3］ 孙洪泉.分形几何与分形插［M］.北京：科学出版社，2011.

［4］ 王正宇，王红玲.基于ARIMA模型的我国GDP分析预测［J］.对外经贸，2011，12：107－108.

［5］ 王 燕.应用时间序列分析［M］.北京：中国人民大学出版社，2005.

［6］ Olivier C，Courtellemont P，Colot O.Comparison of Histograms：a Tool for Detection［J］.European Journal of Diagnosis and Safety in Automation，1994，4（3）：335－355.

［7］ 胡效雷，何祖威.基于GM－ARMA组合模型的年电力需求预测［J］.广东电力，2007（2）：10－13.

［8］ 冯龙龙，李 星，李晓晨，等.GM－ARIMA模型在大坝安全监测中的应用［J］.三峡大学学报：自然科学版，2013，35（5）：7－10.