一种基于Bitmap的虚拟路由表算法的Petri网建模与分析

陈相宇，胡怀湘，张 玉

（华北计算技术研究所，北京 100091）

0 引 言

现代社会里可以依赖虚拟路由来实现客户所特定需要的路由规则。大的ISP通常有很多客户并且有大量的通往不同自治域的路由器，ISP的客户通常对于路由器拥有不同的需求实现。对于金融企业和政府机构的客户来说，他们需要更安全的路由器，然而对于需要实时多媒体业务的客户来说需要的是低延迟和高带宽。为了满足不同客户的需要，ISP应该根据不同客户来分配适合其特色的路由器。然而在现有的BGP协议中，每一个BGP路由器对于每一个数据包只会选着一条看似不错的路径并把它发送给邻居自治域。为了满足更灵活且基于客户要求的路由选择策略，就只能为每个客户分配路由器。这样做无疑是很浪费且很昂贵的，从而在一个路由器上实现虚拟多个路由器是一个不错的选择。

虚拟路由器对于支持客户制定的路由规则、策略路由、多种拓扑结构路由和网络虚拟是一项不错的技术。在策略路由中，不同以往的单靠目的地址来路由，路由选择可能根据的是应用程序、协议和包的大小。在多种拓扑结构路由中，配置不同独立拓扑的路由来提供不同的服务。一个独立的拓扑路由是一群路由和链接的子集，例如对于需要隐私保护的一个拓扑，一个路由子集就可以排除掉那些不安全的的链接或者路由。在这种方法中，需要同时几个本地转发信息库（FIB）来转发数据包。同样虚拟路由对于简化网络管理和减少潜在的网络扰乱也有一定的意义。同时虚拟路由对于研究人员实现并且评估新的网络协议和网络架构有不错的效果。现在在虚拟路由中最核心的技术是路由的可扩展性和性能。对于一个实际的路由器，它可能需要支持几十个或者上百个的虚拟路由并且每个虚拟路由都需要一个他自己的FIB。而且高速率的数据包到达的时间间隔是不一定的，这样就更加要求逻辑上的路由器能够同时支持所有的FIB。为了提供有效的数据转发和IP地址路由，所有的FIB必须存储在读取延迟低的存储体中。在通用处理器中的CACHE大小或者TCAM的内存大小都不足以满足很多的FIB同时存储。例如：在juni⁃per的路由器中，只能最多支持16个左右的虚拟路由。

当进行IP地址查找时，通过咨询FIB路由器从数据包中提取出目的地址来决定下一跳目的地址。在现有的主干网络上，一个FIB一般是包含250 KB个以上的路由表项。所有表项加起来大约是1.5 MB左右。当用软件来实现路由算法时，可能需要的内存更多了。当几个FIB同时存储在一个路由器上面，所需的内存更多。如果直接用TCAM或者SRAM存储的话，系统不仅复杂而且耗钱。若用软件实现，现在通用CPU的CACHE一般只有2 MB左右，这明显小于所需要存储所有FIB的内存大小。这样实现一个共享的能够存储多个FIB的数据结构至关重要。这数据结构不仅要小而且能实现有效的查找。

1 现有虚拟路由方案简介

1.1 简单的Trie树合并

一个FIB包含一系列前缀，每个前缀都有其相应的长度和下一条的地址。可以把FIB对应转化为一个树，如图1所示。

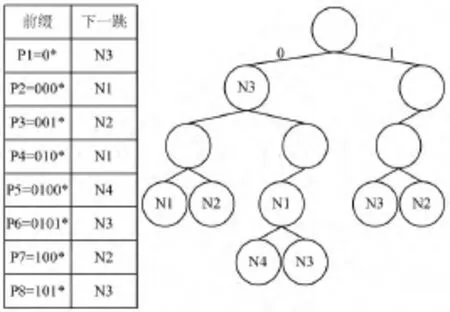
图1 FIB转化图示

当有多个FIB在同一个逻辑路由器上，首先，用最直接的方法在共享的数据结构上存放所有的FIB，即把所有的FIB存储在同一个树上。如图2所示。

图2 FIB存储图示

这种方法每个节点都需要存放每个FIB的表项并且用0表示某个节点没有FIB的表项，这样基本上就等于所有FIB的的表项。每个节点很大，比如一个表项是P大小，那么对于能够实现100个FIB的虚拟路由器来说，这个节点的大小为100P，这样的话当查找每个节点时，一次存储器读取可能会不够，需要多次以上的读取。对于最长前缀匹配的方法，可能需要多次的访问节点。以往的单个FIB访问每个节点的时候只需要读取一次存储器。

1.2 基于Leaf Pushing算法的合并

接下来，探索是否能对于每个树节点的查找只进行一次存储器读取。对于最长前缀的匹配，需要存储最近的匹配项，使得在进一步的匹配中没有能够匹配上的项时，使用最近一次的匹配项。为避免写存储器，只能把最长匹配法变成精确匹配法。在这种方法里面，所有的前缀都存储在叶子节点中，这样的话中间节点便不需要存储FIB表项。构建共享数据结构的第一步，便是所有FIB的前缀集合转化为一个共同的前缀集合。通过加入一个默认的前缀N0，使得集合完全。第二步，通过把聚合的前缀推往他们的子节点，使分支集合不相交。最后一步便是节点收缩，如果一个节点有2个相同的子节点的话，那么他们可以被删去并保留他们父亲节点。构建所需的时间复杂度为O（M），M是树节点数目。构建过程如图3所示。

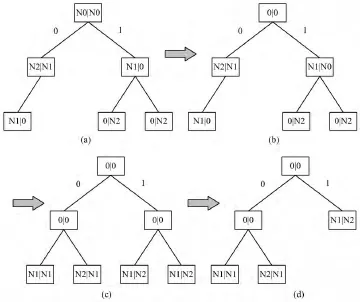
图3 构建树的图示

当数构建完后，需要构建一个树节点序列、共享的下一跳表和所有的下一跳地址端口表。如图4所示。

树节点序列包括树节点的分支值和指向端口的指针。因为树是完全树，所有一般代表2N个子节点。对于中间节点，指针指向的是它最左边的节点。对于一个叶节点，指针指向的是共享下一条表的某个项目。假设在一个路由器中下一跳地址的数目少于256个，这样的话需要1 B便能标示每个FIB。对于T3和T4来说，他们都同时指向N1，这样就可以减少共享下一条表的大小。总的来说：共享下一跳表项比所有的FIB的下一跳表项的总和要小。

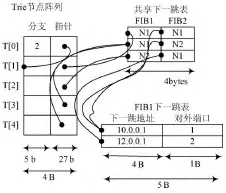
图4 所有下一跳表地址端口表构建图示

构建这个数据结构的步骤为：

（1）构建所有的虚拟路由的下一跳地址端口表；

（2）构建共享下一跳路由表，这一步通过遍历所有的前缀集合，对于每一个前缀只有没有相同的时候才能建立。对于冗余的更新下一跳表项的需要移除出去；

（3）构建树节点序列。

然而对于构建这种算法，这种树上的前缀节点集合大小要大于直接的前缀直接。这种算法的更新也有一定的困难。如果只是对于某个长24 b或者16 b的前缀进行更新，那么只需要一部分的更新，但是如果是对于默认路由那么就要更新很多地方了，如图5所示。

图5 构建树节点序列图示

对于移除一个前缀来说可能会导致的是大部分的更新，这样的话对于删除操作来说就不能在树上面进行从而降低复杂度。但是这样需要额外的存储空间容纳新的树节点队列、共享的下一跳表和下一跳地址端口表。注意这种更新操作可能导致和开始创建的树结构完全不一样，这样的话需要定时的从新建造树。

1.3 基于Braiding算法的改进

然而对于这种方法的评估并不能得到很好的效果。因为它要求2个树基本上相同。当2个树如果相差很大，比方说一个从0开始，另外一个从1开始，则得到的合并树并不能比分开存储有多大的优势，如图6所示。

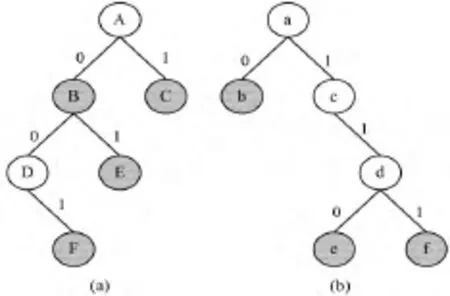
图6 合并前两个相差大的树

对于这2个树的合并得到的树如下。像这样得到的leaf pushing树节点就多很多了。如图7所示。

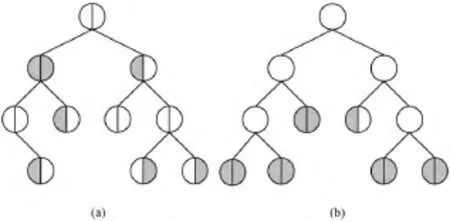
图7 2个树合并图示（一）

根据树的结构，可以对树进行一定的处理来使得刚开始的树是大致一样的。就是在每个节点上都可以任意的调整其左右子树，调整位置标示为1。如把图6中（b）树根节点的左右子树互换，这样就可以使2棵树大致形状相等，然后再进行leaf pushing就有效的多。合并后如图8所示。

图8 2个树合并图示（二）

然而对于这样的算法来说，虽然说总体上节点数目减少了，但是不是叶节点的节点需要的存储空间变为了O（M+2P），M是虚拟路由的数目，P是指针的大小。这样消耗的存储空间也不小。并且这种方法只对于路由表有不同结构的时候有效。

2 基于Bitmap的虚拟路由表结构设计

2.1 数据结构设计

为叶节点信息设计了一种新的数据结构。

对于8个FIB的合并，Bitmap值定义为8位，每位对应一个FIB。其中为1的位标示相应FIB在此节点存在匹配端口，指针指向一个特殊的端口表用以完成匹配；0则标示不存在，需取最近的存在匹配端口的父节点做匹配。端口表每一行中的Bitmap位值均代表相应FIB表中是否匹配紧跟其后的下一跳，若为1代表匹配，若为0则在下一行比对Bitmap。Bitmap为全1的行，表示此行为结尾行，其他未匹配上的均匹配此行下一跳。末尾一般建议留出几行空白行，用于表项的添加，如图9所示。

图9 数据结构设计图示

2.2 性能评价

2.2.1 简单合并方案

低效、高成本，节点体积太大，读取操作多；更新速度快，算法简单。

2.2.2 Leaf Pushing方案

Trie体积减小，共享下一跳表比原来大大缩小；前缀节点集合比原来大，更新算法复杂。

2.2.3 Braiding方案

Trie树整合度高，压缩了表的体积；需要周期性更新Trie树。

2.2.4 Bitmap方案

在FIB数量较多时，减少冗余效果十分明显，更新算法容易实现；但在FIB数量庞大而某节点冗余极少时，效果不明显。另外，本设计中Bitmap位数必须先确定，当虚拟路由表很多时，Bitmap位数也将对应增长，这是本方案的一个待改进之处。

为了比较算法空间复杂度，设计了模拟实验，并根据实验结果做出曲线图。

Trie树节点数据结构：

unsigned char pos；//本node要比较的位在32位IP中的偏移

unsigned char bits；//表示这个节点的孩子节点的位数，比如如果有2个孩子，那么需要1位，0表示第一个孩子，1表示第二个孩子；如果有4个孩子就需要2位，以此类推

unsigned int full_children；//表示孩子中有几个是full的，所谓的full就是在插入操作的时候不能把这个孩子作为新插入的孩子的孩子从而扩展了。

Bitmap表项数据结构：

路由表项数量为250 KB个时bitmap算法与简单Trie树合并算法的路由表大小比较，见图10。

图10 路由器大小比较图示

2.3 进一步设计

通过上述介绍可以发现，本设计是基于对叶子节点的冗余信息的优化。它本身没有改变Trie树整体结构。因此，只要是适用于Trie树结构优化的算法和设计，理论上都能适用于本设计。

在进一步的设计中，考虑加入Braiding方案对Trie树结构的优化压缩，这样虽然提高了算法复杂度，但可以进一步压缩储存空间。而且对于Braiding方案，当Trie树结构逐渐恶化，只需花费少量资源定期更新Trie树，即可实现大部分时间空间和时间资源的有效压缩。对于时间和空间资源分配的平衡性和算法效率的评价工作我们将在进一步工作中进行。

3 Petri网简介

1962年，德国的C.A.Petri在他的博士论文《用自动机通信》中首次使用网状结构模拟通信系统，这是Petri网建立系统模型的起点。Petri网兼顾了严格定义与图形语言两个方面，具有丰富而严格的模型语义，同时又是一种图形化的语言，具有直观、易懂与易用的优点。它采用库所（Place）、变迁（Transition）、弧（Arc）的链接来表示系统的功能和结构。

库所表示系统中的条件、资源和信息等可以静态表达的事物，在图形具体表示中，用圆圈“○”或椭圆表示。变迁表示系统中的变化，如状态的变化、条件的变化、信息的流动以及资源的消耗和产生等需要动态表达的事件，用矩形“口”或短棒“|”代表。弧表示库所与变迁之间的流关系，用“→”来表示有向弧，用“—○”来表示抑制弧（Inhibitor Arc）。token表示库所中代表的事物的数量，用黑点“•”表示库所中含有的托肯。

4 Petri网建模分析

用Petri网理论建立起路由器内部模型见图11。

图11 路由器内部模型

Petri网模型中库所及变迁含义：

P1为路由器缓存，它接收服从泊松到达的数据包，其容量以一个限制弧权来表示；

P2表示路由器CPU闲置状态。当同时满足缓存中有数据包，且路由器闲置时通过即时变迁T1，CPU进入路由表查找态P3；

P5表示路由表的“整齐程度”，它的值用以度量路由表的匹配速度，其值为0时，路由表需要更新，即经过变迁T5进入P6“路由表混乱态”；

当P6和P2同时满足时，CPU经T3执行路由表整理操作，这里定义T3优先级比T1高；

T4表示整理路由表操作，其操作速度为路由表混乱度的函数，T2表示路由表查找操作，其速度也由路由表混乱度决定；

P0态用以实现系统闭环，其Token数可由实验测试得到。

初始状态下，路由表处于整齐态，即P5为1；CPU处于闲置态，即P2为1。

分析过程中，需要确定的函数有：路由表查找速度，即T2变迁速度函数；路由表恶化速度，即T5变迁速度函数；路由表整理操作速度函数，即T4变迁速度；路由器工作周期，即T6变迁速度。

5 结论和展望

本文提出了一种新的基于Bitmap的路由叶子节点冗余信息的压缩储存结构，并借鉴前人工作，结合Braiding方案对本设计进行了进一步压缩，使得虚拟路由表结构从理论上得到大大压缩。至此，本设计工作已完成对构想的设计和建模。进一步工作需要进行仿真实验和网络测量工作，以确定模型参数。进而希望能通过对Petri网络模型的分析，得出对本设计的改进和优化有意义的参考。

[1]范晓勃，林闯，吴建平，等.分布式路由器的性能模型与分析[J].计算机学报，1999（11）：1⁃6.

[2]FU Jing，REXFORD Jennifer.Efficient IP⁃address lookup with a shared forwarding table for multiple virtual routers[C]//Pro⁃ceedingsoftheACM CoNEXT.New York， NY， USA：ACM 2008：4012⁃4033.

[3]SONG Hao⁃yu，KODIALAM Murali，HAO Fang，et al.Building scalable virtual routers with Trie braiding[C]//Proceedings of IEEE Conference on INFOCOM.[S.l.]：IEEE，2010：1442 ⁃1450.

[4]DRAVES R，KING C，VENKATACHARY S，et al.Constructing optimal IP routing tables[C]//Proc.of IEEE Infocom.[S.l.]：IEEE，1999：111⁃120.

[5]SRINIVASAN V，VARGHESE G.Fast address lookups using controlled prefix expansion[J].ACM Transactions on Computer Systems，1999，17（1）：1⁃4.

[6]DEGERMARK M.Small Forwarding Tables for Fast Routing Lookups[C]//Proceedings of ACM SIGCOMM Conference’97.[S.l.]：ACM，1997：3⁃14.