浅析习题教学过程中深层价值的挖掘及策略
2015-07-22成爻兵
成爻兵
[摘 要] 在数学教学过程中,习题教学的价值远远不仅仅是为了应试和升学,也不仅仅是为了提升学生的解题能力,而是通过习题教学行为的开展来提升学生的综合素养,通过综合素养的全面提升来顺势促使学生应试能力的提升,这正是我们在习题教学过程中需要挖掘的深层价值.
[关键词] 情境;价值;变式;智慧;自主
在我们的数学常态教学过程中,教师有一半的时间都在进行习题教学和训练,为此,习题课堂中深层价值的挖掘值得教师认真反思和实践. 笔者就十多年的教学经验和实践反思,进行初步研究和整理,以引起共鸣.
情境呈现,展现价值
在很多教师心目中,我们的习题教学就是为了服务学生的应试和升学,习题教学的最大价值就是让每个学生的解题速度和正确率都得到充分提升,从而有效地服务于学生的升学,服务于学生理想学校的实现. 而这种观点下的习题教学会产生两个明显的弊端:(1)迷失学生的兴趣. 如果我们的习题教学仅仅是为了应试和升学,那很多学生都会在习题学习和训练的过程中迷失自己的学习兴趣,因为习题的价值太窄,这种价值的狭窄一方面无法满足学生在学习过程中的真正需要,另一方面,反复无常的习题学习和枯燥乏味的习题训练会让学生产生强烈的厌恶感和排斥,只是迫于家长和教师的压力而不得不进行无奈的习题学习. (2)扼杀学习的动力源. 习题活动是数学学习活动中的一种主要形式,它是巩固知识与技能、提升学生对知识与技能应用能力的一种有效方法,而平时的题海战术让学生不知道后面还有多少这样的题海现象,直接扼杀了学生再学习的欲望,抹杀了他们再学习的动力源,直接影响着学生的后续学习.
为此,我们必须在教学过程中充分展现习题学习的价值,让学生感受到我们的习题不是单纯的解题,而是基于我们实际生活而产生的,是为了服务于我们在学习和生活中的问题解决而生成的. 即使有些基础性的单一题目训练,那也是通过这种基本技能训练来服务于学生实际能力的达成和提升. 为此,我们在教学过程中就要把习题置于客观现实的情境之中,让情境中的实际问题通过习题来得以解决. 比如二元一次方程(组)、二元一次不等式(组)、分式方程、一元二次方程、一次函数、反比例函数、二次函数等,在初中数学的习题教学过程中,这些知识都可以在情境中建立数学模型,把知识与技能渗透到情境之中. 比如下面这道情境题就可以充分呈现我们数学习题的价值:
在美化校园的活动中,数学兴趣小组想借助如图1所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边).
问题1:若花园的面积为192 m2,你能求出AB和BC的长吗?
问题2:花园的面积可能为200 m2吗?为什么?
问题3:花园的面积最大为多少?请说明理由.
问题4:若在P处有一棵树,其与墙CD,AD的距离分别是15 cm和6 cm,要将这棵树围在花园内(含边界,不考虑树的粗细),此时花园面积最大为多少?
简单情境在生活中常见,学生容易接受,但在简单中,方程、函数的模型蕴涵其中,借助情境再设置梯度的设问,学生就会深刻体会知识的本质特征. 这样通过简单情境揭示数学本质的实例还有很多,我们完全可以把这些情境渗透在习题训练过程中,这样不仅可以避免前面可能出现的两个弊端,还会让学生在数学学习过程中感受到数学学科的价值,提升学生的兴趣和动力,促进学生在学习过程中的再提升.
变式引领,智慧变通
在数学教学过程中,很多教师都会采用变式训练的方式,而变式训练不仅能服务学生对题目的理解深度,还可以充分利用变式过程中数学思想的渗透和数学思维的引领来促使学生学习能力的提升. 这也就是我们习题教学过程中的深层价值之一,也正是课程标准中一直追求的思维能力和创新意识的培养.
习题的变式有很多种方法和形式,就初中数学而言,我们的变式一般都是通过不同角度、不同侧面、不同背景等多个方面来变更数学对象或数学问题呈现的形式,使事物的非本质特征发生变化,而本质特征则保持不变或隐含在题目中,在这个过程中,学生的思维能力会得到进一步考验和训练. 比如,学生在变式训练过程中的观察分析能力、归纳总结对比能力、数形转换能力、逆向思维能力等,学生在初中阶段所要构建的思维能力都会在变式的过程中得到非常有效地训练和提升. 比如下面的变式就能达到良好的效果.
原题?摇 如图2,点O是等边三角形ABC内一点,OA=4,OB=5,OC=3,求∠AOC的度数.
变式1?摇 如图3,在△ABC中,AB=AC,∠BAC=90°,点O是△ABC内一点,OA=4,OB=6,OC=2,求∠AOC的度数.
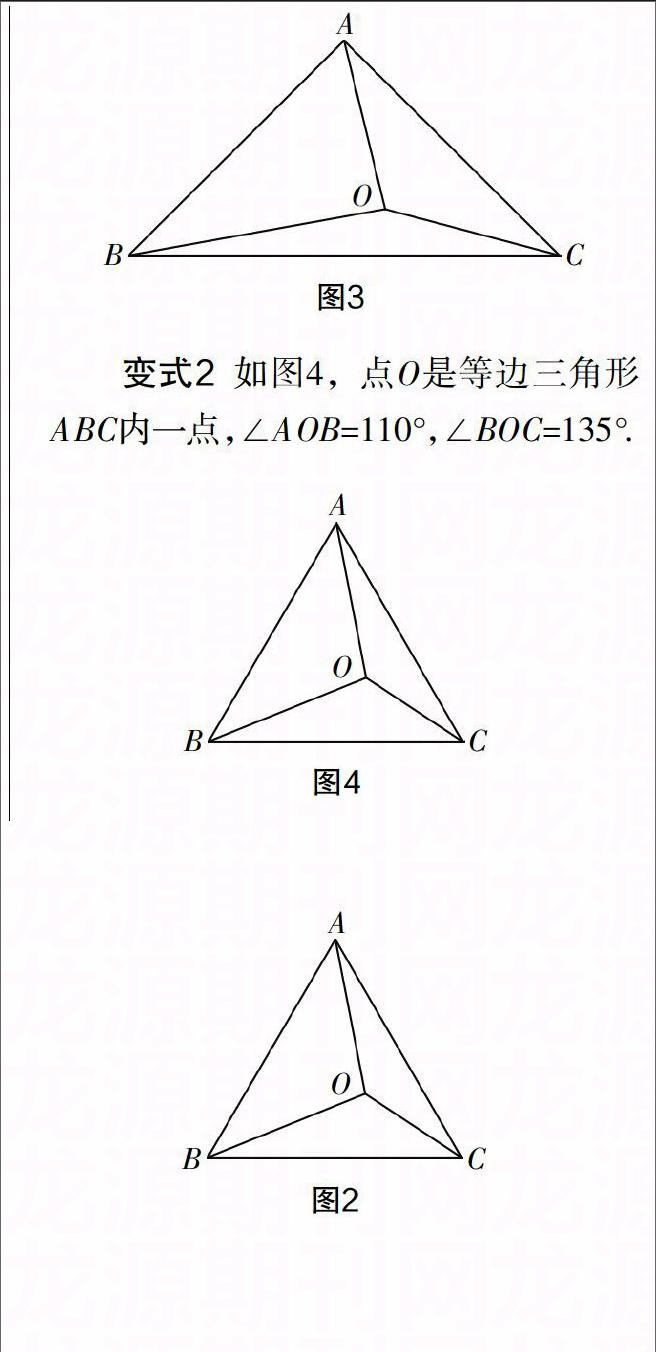
变式2?摇 如图4,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=135°.
(1)以OA,OB,OC为边能否构成一个三角形?若能,请求出三角形各内角的度数;若不能,请说明理由.
(2)如果∠AOB的大小保持不变,那么当∠BOC等于多少度时,以OA,OB,OC为边的三角形是一个直角三角形?
此处的变式不仅充分考虑了学生对三角形性质的掌握情况,还从多个角度考查了学生对相应知识的变通性,充分达到了多维能力的训练和提升. 所以,教师在习题教学的过程中,不仅要注重学生习题的精心选取,提升习题本身的价值,还要精心策划如何将学生易错的题目、重点题目进行变式,以最大效应服务于学生能力的提升,服务于学生数学素养的提升.
自主分析,归纳分类
在初中数学的教学过程中,有一半以上的时间都在进行着习题的训练和讲评,包括教师进行策划的变式训练和讲评,而这种讲授式的教学从教师个人感觉的达成度上和学生的参与度上都得到了教师的认可,因为在这个过程中,教师会认真地板书演练例题,学生会认真地听讲,教师再让学生认真训练和订正,教师再认真地讲评和变式,并让学生进行错题再练和再反馈等. 而这种方式会久而久之地让学生对习题训练感到疲惫和厌倦,失去习题训练更深层的价值. 很多时候,我们可以把空间和时间还给学生,比如习题讲评、错题交流评价等,其中最能体现习题教学的价值就是让学生自己对习题训练进行归纳分类和总结,并学会自己变式与再分析.endprint
比如,在试卷讲评的过程中,教师完全没有必要把试卷按顺序从头讲到位,也没有必要把自己认同的重点反复地强调和演练,而是让学生以小组为单位,对题目进行分析、分类,教师则穿梭在学生交流感悟的过程中,发现问题、适时提醒、巧妙点拨. 学生在整个过程中会对同一类题有一个整体感知,并会发现自己存在的问题和共同存在的共性问题. 这种收获是教师讲评无法达到的. 而在整个过程中,教师可以适度指导. 比如分类,教师可以提醒学生进行三种方法的归类:(1)按知识点归类;(2)按解题方法归类;(3)按答卷中出现的错误类型归类. 例如,对概念、规律理解不透的错误,审题时对题中关键字、词、句子理解错误,思维定式的负迁移,模型建立得不适当,过程分析错误,运算错误等.
服务生活,学以致用
教学的目的绝对不仅仅是为了应试和升学,而是为了提升学生适应生活和进一步发展所必需的数学基本知识、基本技能、基本思想、基本活动经验,而教师在平时的习题教学过程中也要努力注重这些必要素养的渗透和培养. 《义务教育数学课程标准(2011版)》中四个基本领域中就有“综合与实践”这个板块,它要求教师在教学过程中要密切联系“数与代数”“图形与几何”“统计与概率”的知识,而习题教学中的每个环节都可以努力呈现知识与技能中的综合价值和实践意义,借助习题的形式来服务学生的生活和发展,让学生在学习过程中深刻感受到习题训练中多层价值的达成:(1)巩固所学的知识与技能;(2)提升学生对知识与技能的应用能力;(3)展现数学学科的价值和魅力;(4)提升学生的动手操作能力. 为此,教师就要在习题教学过程中为学生创设符合“综合和实践”的习题训练. 比如教学过程中可以把习题中的问题渗透到生活中的实际问题中,让学生为了解决实际生活中的问题而进行生活问题的分析和思考,并努力与所学的数学知识相结合,使知识与问题相结合,真正达到知识与技能相结合、数学与生活相贯通,这就可以达成课标所要求的“综合和实践”的价值所在,并让学生学会用数学知识服务生活,学以致用.
就笔者所教的人教版《数学》教材而言,我们的教学活动中有很多素材可以开展综合实践活动. 如学完“相似”“锐角三角函数”以后,我们可以让学生带上学习工具,走出教室,以小组的形式,利用所学的“相似”和“锐角三角函数”知识进行生活活动开展. 如测量旗杆的高度,学生会经历测量目标的确定、测量方案的制订、测量活动的进行、测量数据的交流等一系列过程. 这一系列过程能真正达到学以致用的效果,会让其价值大大提升.
习题教学的价值是无限的,而无限的价值是完全建立在教师的智慧与勤劳上的,因此,要充分达成习题教学的深层价值,教师还需做进一步的研究和实践,笔者也谨以此文做初步研究,希望达到抛砖引玉的效果.endprint