不可小看的直觉思维
2015-07-22赵久军
赵久军
[摘 要] 解题教学是数学学科的重中之重,笔者认为,在教学中有意培养学生的直觉思维,有助于学生在审题环节中准确找到解题的切入点,提高解题效率.
[关键词] 直觉思维;解题
所谓直觉思维,布鲁纳认为直觉就是一种直接的、非渐进的、以视觉形象为思维媒介的、对问题飞跃式的直接把握和解决. 因而,这种思维方式在操作上是内隐的,表现上是顿悟的,常常能迸发出新异的思维成果,带有创新性,是进行创造性活动的重要的思维方式. 数学最初的概念都是基于直觉,数学发展史上的一些重大发现,如牛顿发明微积分,笛卡儿创立解析几何,高斯对代数学基本定理的证明等,无一不是直觉思维的杰作.
直觉思维在解解答题方面的
价值
数学问题的解决离不开直觉. 解决数学问题时,数学直觉思维表现为不经过逐级分析、严谨论证,而是直接从整体上把握问题实质,迅速敏捷、大胆猜出解题切入点(结论),即直觉先已帮助我们对结论或解题思路产生预见. 实际教学中往往偏重演绎推理的训练,强化形式论证逻辑的严密性,这往往忽视了直觉思维在解题中的预知导向和顿悟作用,也失去了数学思维形成过程中直观生动的一面,在一定范围上限制了学生思维素质的提高,与素质教育的要求背道而驰,所以在数学教学中应注重培养学生的直觉思维.
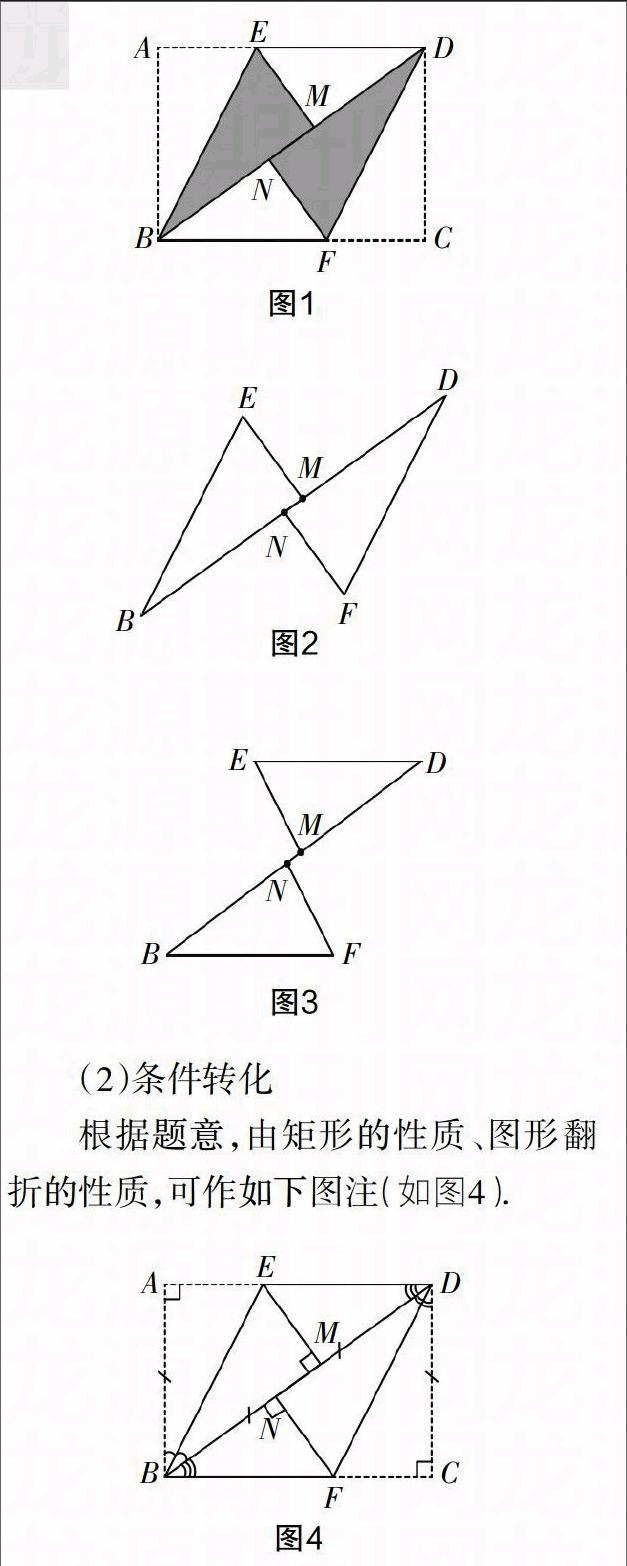
例1?摇 如图1,在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E;将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
1. 对于第(1)问
(1)直觉发现
由于图1中的阴影部分是出题人特意给出的,所以,在学生识图的过程中,自然更容易从图1中提取出图2和图3两个图形,这两个是学习三角形全等时的常见图形,所以,从学生的直觉看,必然会认为通过证明图2或图3中的两个三角形全等是问题解决的切入点.
(2)条件转化
根据题意,由矩形的性质、图形翻折的性质,可作如下图注(如图4).
(3)解题思路
在本问的解决中,如果选择“一组对边平行且相等的四边形是平行四边形”来证明,图2、图3都可取,即通过三角形全等来证明,这对于基础扎实的学生来说,就是书写的问题,而不必费心思考. 当然,作为教者,必须让学生认识到:用图3证明比用图2证明来得更简便些;如果选择“两组对边分别平行的四边形是平行四边形”(定义)来证明此问,则要把图2、图3看成一个整体来思考,借助“内错角相等,两直线平行”即可解决问题. 这种方法比通过证明三角形全等来解决显得更简便.
从教学情况来看,大部分学生是通过三角形全等来证明的,只有很少一部分学生是通过定义来证明的(当然,这部分学生的成绩较优异). 充分训练学生凭直觉解题,虽有时会用时长一点,但这是提高解题效率和正确率的一个可取方法.
2. 对于第(2)问
第(2)问的条件发生了变化,即四边形BFDE变成菱形,那么图形相应地也要发生变化. 学生可以重新画个图,这虽会耽误时间,但能帮助我们解决问题,而不至于什么都写不出来. 如果不重新画图,那又该如何做呢?
(1)直觉1:从基本图形入手
由原图,凭直觉,学生不难提取出图5这一典型图形(实线部分为菱形的一半),再根据“菱形四边相等”这一性质入手进行标图,根据等腰三角形的性质易证BD=2DN=2DC=2AB=4,再在Rt△BCD中由勾股定理即可求得BC. 这是命题人想要的解题思路,当然这是不重新构图的一种解法.
(2)直觉2:利用特殊角的三角函数值解直角三角形
条件只给了AB一条边的长,而要求出同为矩形一条边的BC的长,是否会存在特殊角呢?这是基础扎实的学生拿到题目后的一种本能想法——直觉思维.
于是,由翻折、“菱形的对角线平分一组对角”这两点入手进行标图,学生便发现了∠EBA=∠EBM=∠DBC=30°,由此,利用特殊角的三角函数可求出BC. 虽说现行多种版本的教材里“在直角三角形中,30°角所对的直角边等于斜边的一半”这一定理不再直接用了,但是特殊角的三角函数对九年级学生来讲应该不是难点. 这一解题思路,回避了图1与问题(2)题意不合之不足,是不同于命题人思路的另一解法,但从直觉思维角度来说,又是一个必然.
直觉思维在选择题、填空题方
面的价值
直觉思维不仅在解决以上解答题方面有其特有的价值,其在一些诸如选择题、填空题等小分值问题上也常会使分数来得易如反掌.
例2?摇 如图6所示,已知等腰梯形ABCD的下底BC与上底AD的差恰好等于腰长,AB∥DE,则∠DEC等于( )
A. 75° B. 60° C. 45° D. 30°
面对如此标准的图形,学生“凭直觉”也能猜出答案是多少,而无须怀疑自己,理由是:求角的度数,但题目中没有给出任一角的度数,这只能说明所求的这个角所在的图形是一个特殊的图形,诸如正多边形、等腰直角三角形、长方形等,而此题中的∠DEC是△DEC的一个内角,那么,这个三角形要么是等边三角形,要么是等腰直角三角形,因为规范试卷的图形是标准的,所以学生自然想到∠DEC是等边三角形DEC 的一个内角,即为60°而不是45°.
数学来源于直觉,直觉能帮助我们解决问题. 通过以上例题的分析我们知道:当通过对所要解决的数学问题的结构特征、数据特征、图形特征等的观察和分析,启动直觉思维,进行合情推理,可以快速而有效地解决问题,但作为数学教师的我们,应该在教学中多关注学生的直觉思维培养. 当然,我们同时也要认识到,直觉思维是以已有的知识和经验为基础的,只有具备了坚实的知识基础,积累了丰富的数学经验,加以迅速的判断力和敏锐的想象力,才能产生直觉思维.
爱因斯坦认为,在科学研究和创造发明中,“真正可贵的是直觉思维”. 当然,我们同时也要认识到,在没有经过严格的推理论证和计算之前,就能够对问题作出判断、得出结论或预见解题途径,这并不是主观臆断,而是以对学科知识的深刻理解为基础,以对事物的敏锐观察为前提的,是创新型人才的必备素质,作为教师的我们,应该在教学中多关注学生直觉思维的培养.endprint