例说物理解题结果中整数n的确定
2015-07-22阚兴高徐克田
阚兴高 徐克田
在解某些物理题的过程中,时常会遇到有关多少次、多少人、多少个等整数n的确定问题,现以下列例题来说明物理结果中整数n数值的确定类型和方法.
一、n为不确定的数值
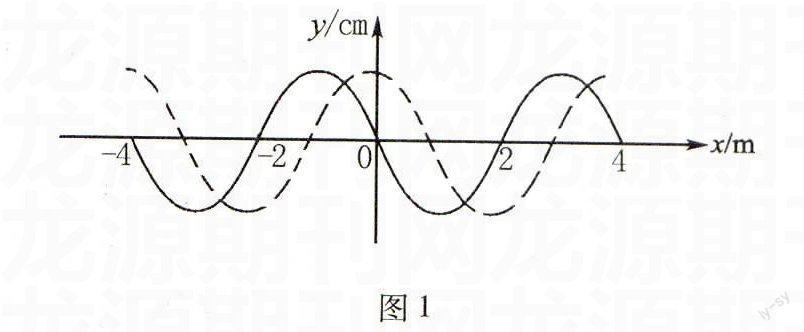
例1如图1所示,实线为一列简谐横波在某时刻t的波形,虚线为时刻(t+Δt)的波形,波沿x轴传播且Δt=0.2s,求该波的波速多大?
解析由图1所示,该波波长
λ=4m.因为波沿x轴传播,而且具
有传播方向的双向性及振动的周期性,
所以应对它进行如下讨论:
若波沿x轴正方向传播,它在Δt时间内通过的距
离
Δx1=(n+34)λ=(4n+3)m,(n=0,1,2,…)
∴波速υ右=xt=(20n+15)m/s, (n=0,1,2,…)
若波沿x轴负方向传播,它在Δt时间内通过的距离
Δx2=(n+14)λ= (4n+1)m, (n=0,1,2,…)
∴波速υ左=xt=(20n+5)m/s, (n=0,1,2,…)
即该波波速的大小为(20n+15)m/s或(20n+5)m/s,其中n=0,1,2,….
由此可知:对于无条件限制且具有周期性的题目,所求结果中的n是整数且为不确定值.
二、n有确定的数值
在解题结果含有n且n为确定整数中,其结果中的整数为一个或几个,即解题结果有唯一解和多解两种情况:
1.n有唯一值
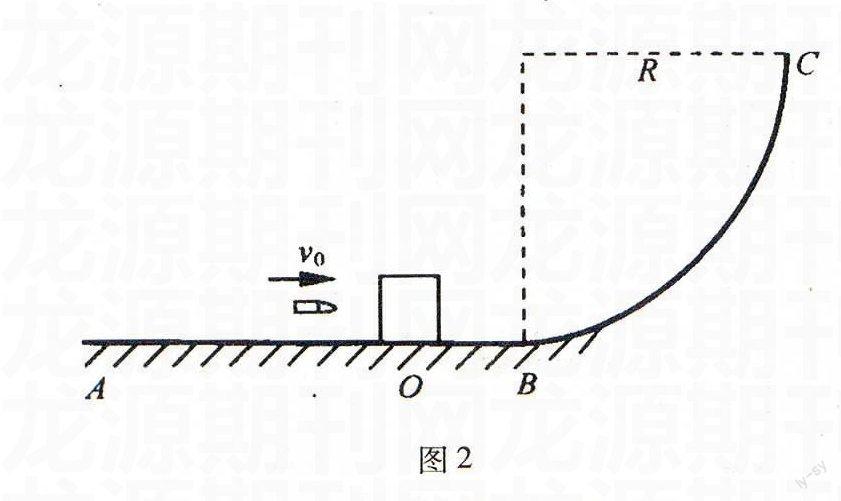
例2如图2所示,AOB是光滑水平轨道,BC是半径为R的14光滑圆弧轨道,两轨道恰好相切,质量为M的小木块静止在O点,一质量为m(m=M9)的子弹以某一初速度水平向右射入小木块内不穿出,木块恰好滑到圆弧的最高点C处(子弹、小木块均可看成质点).求:当第n颗子弹射入小木块后,小木块沿
圆弧上升的最大高度为R4,则n值是多少?
图2解析对M、m,由动量守恒得:
mv0=(M+m)v1①
从B→C,由机械能守恒得:
12(M+m)v21=(M+m)gR
②
当小木块返回到O点时,它与开始时的动量大小相等、方向相反.由动量守恒得:当第2、4、6、…n(n为偶数)颗子弹射入小木块后,小木块的速度均为零,即在O点,小木块上升的高度为零,故只有第奇数颗子弹射入小木块后,小木块上升的高度不为零,由动量和能量守恒:
mv0=(M+nm)vn③
12(M+nm)v2n=(M+nm)gR4④
由题:m=M9⑤
由①~⑤解得:n=11,即n的值为11.
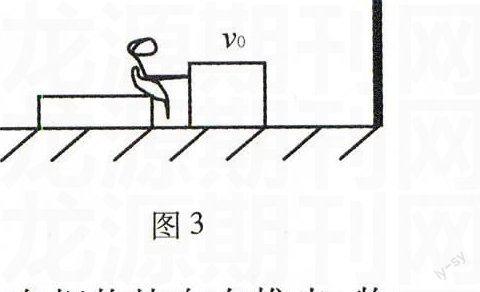
例3如图3所示,在光滑的水平面上,停放着一物块和载人小车,人与小车的质量为M,物块的质量为m,且M
∶m=16∶1,当人相对地以v0沿水平方向把物块向右推出,物块与墙壁相碰后又以同样的速率(相对地面)返回,若物块与墙发生正碰且碰时无能量损失,求该人经过多少次推物块后,再也推不到物块了?
解析
对M、m,选水平向右的方向为正,由动量守恒得:
推第一次,0=mv0-Mv1′①
推第二次,-mv0-Mv1′=mv0-Mv2′②
推第三次,-mv0-Mv2′=mv0-Mv3′
③
……
推第n次,-mv0-Mvn-1′=mv0-Mvn′
上述各式相加得:vn′=(2n-1)mv0M④
人推不到物块时满足vn′≥v0⑤
M∶m=16∶1⑥
由上式解得:n≥8.5,再根据题意可得出n=9,即该人经过9次推物块后,就会再也推不到物块了.
例4如图4所示,质量M=10 kg,上表面光滑足够长的木板在水平拉力F=50 N的作用下,以v0=5 m/s初速度沿水平地面向右匀速运动,现有足够多的小铁块(可视为质点),其质量均为m=1 kg,将一铁块无初速地在木板的最右端,当木板运动了L=1 m时,又无初速地放在木板的最右端放上第二个铁块,只要木板运动L,就在其最右端无初速地放一铁块,求:
最终有几个铁块能留在木板上?(g=10 m/s2)
解析
对M,由于匀速运动,所以F=μMg①
当第一个铁块放上后,木板开始做匀减速直线运动,对木板,由动能定理得:
放第一个铁块,-μmgL=12Mv21-12Mv20
放第二个铁块,-μ×2mgL=12Mv22-12Mv21
放第三个铁块,-μ×3mgL=12Mv23-12Mv22,……
放第n个铁块,-μnmgL=12Mv2n-12Mv2n-1
上述各式相加得:
(1+2+3+4…+n)μmgL=12Mv20-12Mvn
②
木块停下,vn=0③
由①、②、③解得:n=6.6,而n为整数,究竟n等于6还是等于7呢?这就要根据题意来确定,由于木块在放上铁块后,分别做不同的匀减速直线运动,故木块的速度越来越小,最终停下,木块开始的动能全部转化内能,故若n=6,即木块上最多有6个铁块,木块克服摩擦力做的功小于木块开始的动能,这样,木块将不会停下;若n=7,即木块上最多有7个铁块,木块克服摩擦力做的功大于木块开始的动能,这样,木块将会停下,并且当第7个铁块放上后,木板并没有运动一个完整的L而停止,故符合题中要求的n应等于7.
例5如图5所示,滑块A的质量为m=
0.01kg,与水平地面间的动摩擦因数μ=0.2,用细线悬挂的小球质量均为m=0.01kg,沿x轴排列,A与第一个小球及相邻两小球间距均为s=2m,线长分别为L1、L2、L3、….(图中只画了三个小球),开始时,滑块以速度v0=10m/s沿x轴正方向运动,若不考虑滑块与小球碰撞时损失的机械能,碰后小球均恰能在竖直平面内完成完整的圆周运动,L1<2m,小球刚好不接触地面,求:滑块能与几个小球相碰?
解析物体A沿水平面向右做匀减速直线运动,与第一个小球相碰,由动量守恒得,两物体交换速度,
即物体A停下,第一个小球获得了相碰时的速度(设v01)
开始做圆周运动,再与A物体以相同的速度相碰,此时两物体又交换速度,A物体就以此速度v0沿水平面向右做匀减速直线运动,再与第二个小球发生碰撞,依次类推,直到物体A最后停下.设在此过程中,物体A运动了s距离,对A物体,由动能定理:
-μmgs=0-12mv20①
与小球相碰的个数n=sL②
由①、②解得:n=12.5,根据题意,A物体与第12个小球发生碰撞时,A物体已运动了12 m,它还能向右运动0.5 m,而0.5 m小于2 m,故A物体不能与第13个小球相碰,因此,此题中的n应等于12.
由此可知:对于n有唯一数值的结果,如果n恰好为整数不需分析;对于结果含有n不是整数的等式或不等式,应根据题中的条件来分析确定出某一个确定的数值.
2.n多个值
例6 (1996年全国高考题),如图6所示,一根紧张的水平弹性长绳上的a、b两点,相距14.0 m,b点在a点的右方.一列简谐横波沿绳向右传播时,若a点的位移达到正极大时,b点的位移恰好为零,且向下运动,经过1.00 s后,a点的位移为零且向下运动,而b点的位移恰达到负极大,则这列简谐波的波速可能为().
A.14 m/s
B.10 m/s
C.6 m/s
D.4.67 m/s
解析由于波向右传播,可根据题意及波的周期性,利用“去整取零”的方法,即在a、b间做出不到 一个波长的波形,如图7所示,再利用微小平移法,便可确定出符合题意是图6中的波形②,由波的周期性得:( n+34)λ=14.0,(n=0,1,2,…);由题意并结合图7知:(k+14)T = 1.00,(k=0,1,2,…),所以波速υ=λT=14(4n+1)4k+3m/s,由此可知:当n=k=0时,则υ=4.67 m/s;当n=k=1时,则υ=10 m/s;当n=k=2时,则υ=11.45 m/s,…,由此可得到正确选项为B、D.
由此可知:对于有条件限制且含有整数n或k的题目,应对所求含有通式的结果进行讨论,从而找出符合题中要求的整数.本题中符合题中要求的整数n或k,均只能为0和1这两个数值.
总之,对于我们所求解含有整数n的结果,不论题中有无条件限制,都应结合题中的条件来分析、讨论,这样,就可避免漏解或多解等现象,从而最终保证所求结果的完整性和准确性.
(收稿日期:2015-03-26)
