基于信息熵多属性决策的统计信息综合评价研究

付 沙 周航军 杨 波 肖叶枝

（湖南财政经济学院，湖南长沙410205）

基于信息熵多属性决策的统计信息综合评价研究

付 沙 周航军 杨 波 肖叶枝

（湖南财政经济学院，湖南长沙410205）

〔摘 要〕针对当前权重确定方法单一、传统熵权计算方式不足等问题，构建一种基于信息熵多属性决策的综合评价模型。该模型运用改进层次分析法确定全体决策者对各指标的主观权重，以信息熵理论确定各指标的客观权重，并结合主观与客观权重作为最终评价的综合权重。在此基础上依据多属性决策模型提出多属性决策评价方法，该方法将主、客观分析相结合，既考虑权重的现实性，又以数据作为评价基础，能有效解决选择评价中的不确定多属性决策问题。论文通过对湖南统计年鉴中数据的分析，验证了所提方法的可行性与有效性。

〔关键词〕信息熵；多属性决策；统计信息；综合权重

多属性决策（Multiple Attribute Decision Making，MADM）是现代决策科学的一个重要组成部分，主要用于解决多个属性情况下的有限方案决策问题，其实质是利用已有决策信息，通过一定方式对有限个备选方案进行排序择优。其理论和方法已广泛应用到社会生活、工程设计、系统工程以及管理科学等领域。现实生活中，由于人类思维的模糊性以及客观事物的复杂性与不确定性，人们在决策过程中对评价事物往往难以给出确切的数值，而是以模糊数等形式的不确定信息来评定［1］。此类决策问题目前在国内外专家学者中有着较高的关注度，如文献［2］利用信息熵理论对多属性决策指标进行规范化处理的方法，得到了待决策方案的优化属性值，从而达到更为精确地判断决策方法优劣的效果。文献［3］通过将信息熵引入到不确定多属性评价决策模型中，建立了我国商业银行操作风险的多属性评价方法。文献［4］针对多属性决策过程中同时存在多种特征的定性与定量不确定信息，且属性权重未知的情况，提出基于不确定信息熵和证据推理的不确定多属性决策方法。文献［5］运用信息熵和结构元理论，探讨了权重完全未知情况下的模糊多属性决策方法，构建了模糊多属性决策模型，并将该方法运用到干部考核、评估等问题中。

湖南幅员辽阔，物产富饶，俗有“湖广熟，天下足”之谓，是著名的“渔米之乡”。全省辖13个市、1个自治州、122个县（市、区），在这片三湘大地上，生活着汉、土家、苗、侗、回等56个民族7 090万湖湘儿女。全省实有耕地总资源378.9万公顷，至2010年底，全省有林地面积1.51亿亩，森林覆盖率为57.01%。主要农副产品产量如粮食、棉花、油料、苎麻、烤烟及猪肉等均位居全国前列。湖南矿产丰富，矿种齐全，是驰名中外的“有色金属之乡”和“非金属矿之乡”。基于上述描述，以湖南统计信息网发布的2008-2012年《湖南统计年鉴》中“湖南的一天”数据为例，根据信息熵多属性决策的综合评价模型对其进行分析与评价。

1　信息熵的概念

熵的概念最早由Clausius于1865年提出，之后信息论之父C.E.Shannon在1948年将熵的概念引入信息领域，利用“信息熵”作为衡量信息紊乱程度的测度［6］。熵的概念从宏观上反映了系统在微观状态下的不确定性程度。

信息熵（Shannon熵）在随机事件发生之前，它是对于结果不确定性的量度；在随机事件发生之后，它是从该事件中所获信息的量度（信息量）。信息熵是系统无序程度的度量，其某项指标的指标值变异程度越大，信息熵越小，该指标所提供的信息量越大，其权重也应越大。信息熵的运用可减少确定指标权重的主观性与随意性。在信息论中，信息熵用于表示系统的不确定性。它是多属性系统的一个状态函数，熵值越大，表明系统越不确定，越无序；熵值越小，则该系统越高效有序，且经济效益越高。

假设系统可能处于n种不同状态：｛S1，S2，…，Sn｝，Pi表示系统处于状态Si下的概率，其中i＝1，2，…，n，0≤Pi，则系统X的熵为：

熵具有极值性，当系统状态为等概率，即Pi＝1／n时，熵取最大值Hmax＝lnm，利用Hmax对式（4）进行归一化处理得到衡量各指标的相对重要性熵值为：

当pij（j＝1，2，…，m）取等值时，熵ei为最大值1，即ei满足0≤ei≤1。

2　基于信息熵多属性决策的综合评价模型构建

2.1问题描述

对于某一多属性决策问题，假设方案集为A＝｛A1，A2，…，Am｝，属性集为C＝｛C1，C2，…，Cn｝，属性的权重向量为w＝｛w1，w2，…，wn｝，且。本文依据各方案属性值的表达，分析探讨如何构建基于信息熵多属性决策的综合评价模型。

2.2算法步骤

针对文中探讨的基于信息熵多属性决策的综合评价模型构建，其具体步骤如下：

Step 1依据给定各方案在各指标下的评价值，构造m个方案n个评价指标的判断矩阵A＝（xij）m×n，xij表示第i个方案的第j个指标值。

Step 2判断矩阵的规范化处理。为消除指标间由于量纲不同而影响决策结果，可对指标值的判断矩阵进行规范化处理，由此得到规范化决策矩阵Y＝（yij）m×n。

在多属性决策问题中常见属性类型为效益型与成本型，效益型指标的值越大越好；而成本型指标的值则越小越好。

效益型指标：

成本型指标：

其中，i＝1，2，…，m；j＝1，2，…，n。

Step 3依据熵的定义确定第j个指标的信息熵值。

Step 4计算第j项指标的熵权［8］。

Step 5计算每个属性的客观权重比重与综合权重。

设每个属性的客观权重所占比重为qj，则主观权重所占比重为pj，且qj+pj＝1，j＝1，2，…，n。

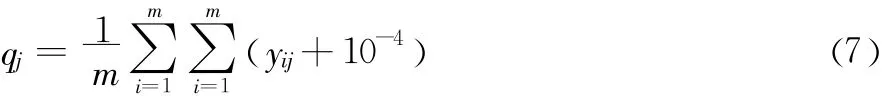
运用模糊层次分析法确定全体决策者对各属性的权重z，计算属性的综合权重wj。

Step 6从方案集A中定义相对的理想方案与负理想方案：

将方案i与理想方案的距离记为

方案i与负理想方案的距离为

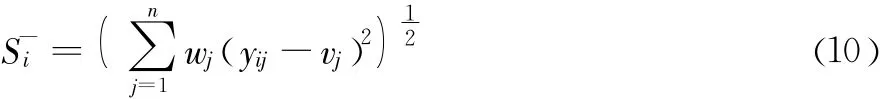
其中，i＝1，2，…，m。

最后，依据Ui的大小进行排序，即可获得最优方案。

3　算例分析

《湖南统计年鉴》系统收录了全省及各市、州、县连续若干年经济与社会发展方面的大量统计数据，以及重要历史年份的全省主要统计数据，是一部全面反映湖南省经济和社会发展情况的资料性年刊。为了更直观地阐述基于信息熵多属性决策的综合评价模型作用机理，本文以湖南省政府统计门户网站“湖南统计信息网”发布的2008-2012年《湖南统计年鉴》中“湖南的一天”子栏目为例［9］，其统计信息评价如表1所示。

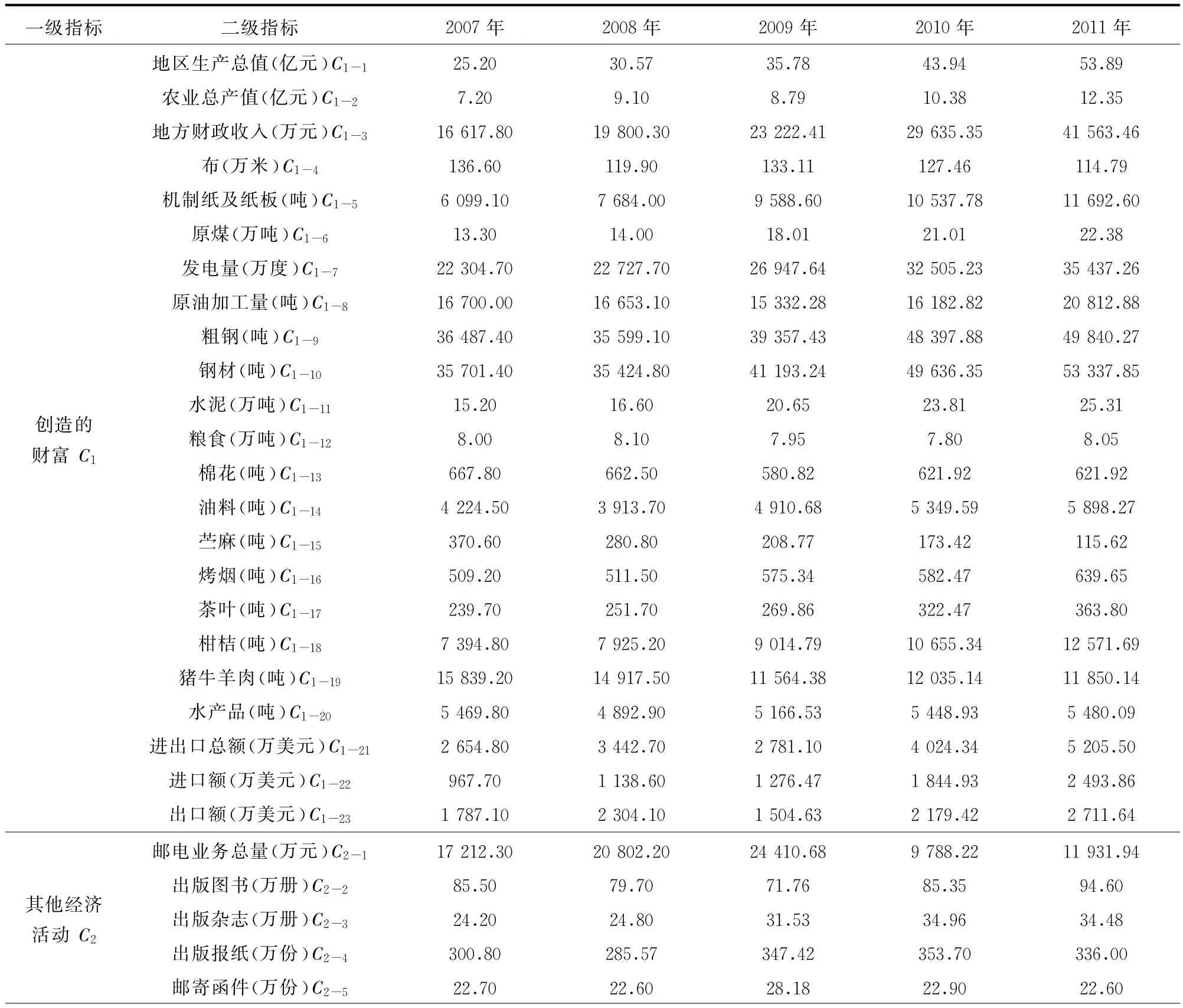
表1　湖南省统计信息评价指标

表1　（续）

（1）依据式（3）～（4）将表1的指标数据进行规范化处理，利用式（5）～（6）计算熵值Hj和熵权ej。

Hj＝（0.76271，0.79490，0.71345，0.79467，0.80970，0.72782，0.67340，0.67941，0.67058，0.64919，0.75950，0.84205，0.82370，0.76668，0.77474，0.67759，0.69317，0.71475，0.61359，0.83747，0.67491，0.68729，0.79573，0.76275，0.82028，0.72323，0.79530，0.17744，0.79338，0.78766，0.82901，0.80689，0.84317，0.71037）

ej＝（0.02871，0.02790，0.02995，0.02790，0.02753，0.02959，0.03096，0.03081，0.03103，0.03157，0.02879，0.02671，0.02717，0.02861，0.02841，0.03086，0.03046，0.02992，0.03247，0.02683，0.03092，0.03061，0.02788，0.02871，0.02726，0.02971，0.02789，0.04347，0.02794，0.02808，0.02704，0.02760，0.02668，0.03003）

（2）根据式（7）可得qj：

qj＝（0.44193，0.45913，0.38293，0.53114，0.54025，0.48909，0.43260，0.32925，0.44510，0.42627，0.50594，0.60010，0.57692，0.47660，0.44806，0.41736，0.40144，0.40914，0.39237，0.67918，0.37917，0.37792，0.49119，0.48161，0.50894，0.53858，0.57441，0.21444，0.53297，0.52690，0.55366，0.49133，0.66328，0.46238）

（3）运用文献［10］提出的模糊层次分析法确定各属性权重z，然后依据式（8）计算属性的综合权重wj。

wj＝（0.02999，0.02958，0.03060，0.02795，0.02774，0.02929，0.02985，0.02893，0.02935，0.03010，0.02840，0.02723，0.02752，0.02829，0.02708，0.02919，0.02899，0.02879，0.02975，0.02720，0.03097，0.03085，0.02947，0.02782，0.02811，0.02938，0.02836，0.03132，0.03030，0.03041，0.02970，0.02984，0.02881，0.03109）

（4）从方案集中定义相对的理想方案f和负理想方案v。

f＝（1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，0，0，1，0，1，0）

v＝（0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，1，1，0，1，0，1）

（5）运用式（9）～（10）得到：

S+＝（0.72798，0.61109，0.39578，0.23426，0.14572）

S-＝（0.17399，0.17148，0.27381，0.43897，0.78846）

（6）根据式（11）可得：

Ui＝（0.19290，0.21912，0.40893，0.65204，0.84402）

由此，“湖南的一天”统计信息评价得分的结果如图1所示。

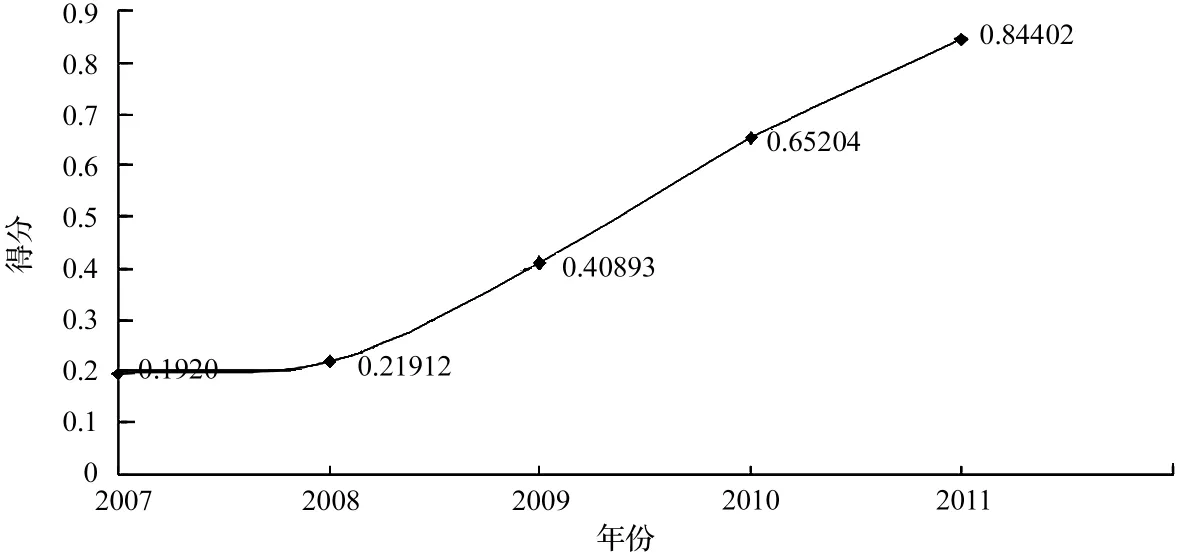
图1　“湖南的一天”统计信息评价得分情况

经湖南省统计局核算，曾以“鱼米之乡”著称的湖南，农业生产已先后被工业及服务业赶超。2011年湖南省经济发展保持平稳较快增长，工业领域增长显著：全省规模工业实现增加值8 122.76亿元，增长20.1%。主要工业产品中，74.1%的产品产量增幅较大，产销率达98.71%，同比提高0.11个百分点。根据图表统计信息整理及分析，得出：原油加工量增长28.6%，钢材增长7.5%，原煤增长6.5%，水泥增长6.3%。2011年原煤较2007年增长68.3%，水泥较2007年增长66.5%，原油加工量较2007年增长24.6%。

与之相比，经济总量位列第三的第一产业中，粮食总产量增长3.2%，猪牛羊肉减少1.5%，水产品增长0.57%，油料增长10.3%，增幅表现平稳。在消费方面，2011年城乡居民消费总额、平均每人消费额分别增长11.3、12.3，较2007年分别增长68.1、78.2。值得关注的二级指标有：2011年邮电业务总量较2007年减少30.7%，苎麻较2007年减少68.8%。

从2008-2012年，我省GDP由11 156.64亿元增长到22 154.23亿元，连续5年列全国前十，增长近2倍。一系列的数据印证了湖南在多方面实力逐步提升：（1）工业生产平稳增长；（2）农业基础地位得到巩固；（3）基础设施不断完善；（4）居民消费保持旺势；（5）外引内联成效明显。从多项数据分析亦可看出，湖南人民同心协力、开拓进取，全省经济建设不断发展，社会事业突飞猛进，综合实力显著增强，人民生活水平稳步提高。

4　结束语

本文首先运用改进层次分析法确定全体决策者对各指标的主观权重，然后应用信息熵理论确定指标的客观权重，再通过建立综合权重模型将决策者的主观权重与样本自身产生的熵权相结合，采取一定的方式混合加权计算综合权重。在此基础上结合多属性决策模型提出多属性决策评价方法，将主、客观分析相结合，既减少决策问题的主观性，又能量化整个评价过程，有效解决了选择评价中的不确定多属性决策问题，具有良好的应用推广与实际决策价值，可广泛应用于供应链选择、项目评估、投资决策以及经济效益综合评价等相关决策问题中。

参考文献

［1］张市芳，刘三阳，翟任何.动态直觉模糊多属性决策的VIKOR扩展方法［J］.计算机科学，2012，39（2）：240-243.

［2］余胜春.基于信息熵的多属性参数系统决策方法［J］.数学杂志，2012，32（6）：1111-1114.

［3］张晨，朱卫东，杨善林.基于信息熵的商业银行操作风险多属性评价方法研究［J］.预测，2007，26（5）：55-58，63.

［4］尹德进，王宏力.基于信息熵与证据推理的不确定多属性决策方法［J］.计算机应用，2011，31（5）：1308-1310，1412.

［5］刘海涛，郭嗣琮.基于结构元理论及信息熵的模糊多属性决策方法［J］.数学的实践与认识，2009，39（17）：1-5.

［6］梁吉业，钱宇华.信息系统中的信息粒与熵理论［J］.中国科学E辑：信息科学，2008，38（12）：2048-2065.

［7］张近东，任杰.熵理论中熵及熵权计算式的不足与修正［J］.统计与信息论坛，2011，26（1）：3-5.

［8］何满辉，逯林.基于信息熵多属性决策的物流供应商选择评价［J］.工程设计学报，2013，20（1）：6-10.

［9］湖南统计信息网.湖南统计年鉴［EB／OL］.http：∥www.hntj. gov.cn／sjfb／tjnj／，2013-07-17.

［10］付沙，廖明华，肖叶枝.模糊层次分析法在信息安全领域中的研究探索［J］.情报学报，2012，31（10）：1105-1109.

（本文责任编辑：孙国雷）

The Statistics Comprehensive Evaluation Research Based on Entropy Multi-attribute Decision Making

Fu Sha Zhou Hangjun Yang Bo Xiao Yezhi
（Hunan University of Finance and Economics，Changsha 410205，China）

〔Abstract〕The paper construct a multi-attribute decision making comprehensive evaluation model based on information entropy，for the single method of weight determining and less calculation methods of traditional entropy weight and other issues.The model uses improved AHP to determine the subjective weighting of each index of all decision-makers，to determine the objective weight of each index based on the information entropy theory，and combined with subjective and objective weight as the comprehensive weight of final evaluation.Then proposed multi-attribute decision evaluation method based on multi-attribute decision model，this method combined the subjective and objective analysis，consider the reality of weight and uses data as the evaluation，it can effectively solve the uncertain multi-attribute decision making problems in selection and evaluation process.The paper verified the feasibility and effectiveness of the proposed method by the analysis of the data in Hunan Statistical Yearbook.

〔Key words〕entropy；multi-attribute decision making；statistics；comprehensive weight

作者简介：付 沙（1980-），男，副教授，硕士，研究方向：决策分析、信息系统安全。

基金项目：湖南省社科基金项目（项目编号：No.14YBA065）；湖南省教育厅科学研究项目（项目编号：No.14C0184）。

收稿日期：2015-06-29

〔中图分类号〕G254.92

〔文献标识码〕A

〔文章编号〕1008-0821（2015）08-0126-05

DOI：10.3969／j.issn.1008-0821.2015.08.024