盾构快速穿越法超浅覆土及负覆土隧道施工预测分析

赵辛玮, 马永其,2, 滕 丽

(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海大学理学院,上海 200444; 3.上海城建(集团)公司,上海 200122)

盾构快速穿越法超浅覆土及负覆土隧道施工预测分析

赵辛玮1, 马永其1,2, 滕 丽3

(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海大学理学院,上海 200444; 3.上海城建(集团)公司,上海 200122)

盾构快速穿越(ultra-rapid under pass,URUP)法隧道施工技术是一种盾构机从地表直接始发掘进,最后在设定目标地点直接掘进到地表的新型施工方法.以南京机场城轨URUP法隧道示范工程为背景,利用三维非线性有限元方法( fi nit element method,FEM),对URUP法隧道施工过程进行了数值模拟.预测分析了隧道施工过程中超浅覆土和负覆土区间的地表变形规律、施工影响范围以及最终沉降值.分析结果与实测数据比较吻合,说明了数值模拟的有效性和预测分析的可信性.

预测分析;盾构快速穿越法;三维有限元模拟;地表沉降

传统的地下盾构隧道施工需要修建施工竖井、地下连续墙,开挖施工引道等.由于基坑和引道等需要大型设备进行施工,施工影响区域和设备本身占地面积大,不仅影响地面交通,而且大型设备施工噪音大,影响周围居民正常生活.为解决上述传统盾构施工方法带来的诸多不便,新的盾构快速穿越(ultra-rapid under pass,URUP)法隧道施工技术应运而生[1].在该施工技术中,盾构机从地表直接始发掘进,最后在设定目标地点直接掘进到地表(见图1).由于将隧道和引道一起施工,无需施工竖井和大开挖施工引道,因此,该技术能够有效减少征地、拆迁以及大型机械设备的使用.另外,由于仅在结构段需要进行土体开挖,在减小土体挖方量的同时也进一步减小了对环境的影响,实现了对土体和能源的高效利用.因此,URUP法隧道施工技术是一种具有良好社会经济效益的新型盾构隧道施工方法,有着广阔的应用前景.

URUP法隧道施工技术最早由日本株式会社大林组于2003年提出并开始研发,2008年首次将其应用于实际工程中[1-2].2010年荷兰的Delft理工大学也开始进行相关的理论研究[3]. Keizo等[2]基于对矩形土压盾构地面始发、到达试验段工程的施工研究,验证了URUP法隧道施工技术在矩形盾构隧道掘进中的可行性.Hitonari等[4]介绍了URUP法隧道施工技术的首次实际工程应用——中央环形品川线(东京都)大井区隧道施工项目.该项目地上道路与地下隧道道路之间的连接段采用了该施工技术,其中圆形断面形式的盾构机首次应用于该工法,并取得了预期效果.Toshiaki等[5]介绍了URUP法隧道施工全过程,列举了该技术的若干关键问题.Yamauchi等[6]以两项URUP法隧道实际工程应用为背景,探讨了盾构机在保持开挖面稳定的条件下,从地面始发大倾角掘进至超浅覆土的施工控制技术.上述文献都是对URUP法隧道施工技术方面的介绍与论述.Brijer[3]将日本的URUP法隧道施工技术进行调整以适应荷兰地下水位埋深较浅的地层环境,分析了该技术与传统盾构法在施工长度不超过250m的地下通道中的应用结果.通过对比研究发现,该技术较常规盾构施工法具有明显的经济优势.张子新等[7]依托URUP法隧道施工技术在我国南京城际快速轨道秣将区间隧道示范工程中的首次应用,探索分析了该方法在工程中主要施工参数的合理选择和有效的控制技术.

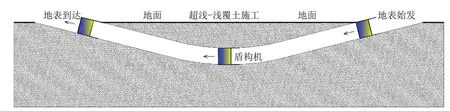
图1 超浅覆土下URUP法隧道施工示意图Fig.1 Construction of shield tunnel with URUP method

由于数值模拟方法具有能够适应复杂边界条件,可以考虑土体与衬砌的相互作用及土体的非线性特性,分析结果全面详细等优点,更适合规律性研究与总结,因此被广泛运用于盾构法隧道施工研究中.为了模拟盾构施工工序、后续地层位移、隧道开挖周围及地表的应力状态等因素对地面沉陷的影响,Lee等[8-9]发展了一种三维弹塑性有限元方法( fi nit element method, FEM),给出了非线性问题的求解步骤和适用于三维隧道分析的弹塑性土体本构模型.王敏强等[10]运用刚度迁移法模拟盾构推进,采用权刚度修正Goodman单元处理存在两种材料的混合接触刚度.张利民等[11]运用三维有限差分软件FLAC3D,考虑了盾构机、注浆压力、土仓压力等因素,对盾构掘进施工进行了数值仿真,得到了一定条件下地表沉降槽和纵向地表变形规律.张海波等[12]在全面分析土压平衡式盾构施工过程中影响周围土体变形各主要因素的基础上,提出了一种能够综合考虑各种因素的盾构施工三维非线性有限元模拟方法.李曙光等[13]使用有限差分软件FLAC3D 模拟分析了地铁盾构法隧道施工诱发的地面沉降.朱合华等[14-15]在有限元分析中考虑了盾构衬砌接头的转动效应和盾尾注浆材料在施工中由液态向固态转化的凝固过程,采用注浆材料的变刚度等效法来模拟其力学变化,并对在均布和非均布注浆压力下,土压力及衬砌内力的计算值与实测值作了比较分析,发现非均布条件下的计算值较均布条件更接近实测值.尚国庆等[16]采用非线性有限元分析软件Abaqus,对超大型泥水平衡盾构在浅覆土工况下的施工过程进行了非线性有限元三维仿真模拟.模型较全面地考虑了盾构施工过程中土体、盾构、管片和浆体之间的相互作用,较好地反映了泥水平衡盾构的实际施工过程.宁寅等[17]运用有限元分析软件Abaqus模拟了泥水盾构沿弧线下穿已有隧道的施工过程,分析并预测了盾构施工对已建隧道和地表的影响.上述文献都是针对盾构在深埋掘进工况下施工过程的数值模拟.

然而,从图1可以看出,在URUP法隧道施工过程中盾构的上覆土厚度是变化的,其整个施工过程将经历负覆土(盾构机部分掘出地表)、超浅覆土(上覆土厚度小于0.5D,其中D表示隧道直径diameter)、浅覆土等施工区段,其中超浅覆土和负覆土施工阶段是传统盾构施工中不曾遇到的问题.由于覆土极浅,土体扰动较深埋施工明显,因此极易造成土体破坏,给施工带来很大困难.朱合华等[18]运用MARC分析系统对某污水管道超浅埋盾构法隧道施工过程进行了三维有限元数值模拟,重点分析了盾构衬砌变形及锚杆受力.张所明等[19]使用有限元数值分析,计算了外滩通道工程浅覆土大盾构施工产生的竖直沉降和水平位移,分析了对邻近已建建筑物的影响.吴惠明等[20]基于上海轨道交通9号线某区间隧道超浅覆土条件下的典型工况,通过对其工程监测试验、施工参数以及控制技术措施的有效性进行分析,得出了对超浅覆土施工有效的控制技术措施.陈林[21]对某地铁出入段线盾构法隧道施工过程的地面沉降监测数据进行了分析,探讨了盾构施工小半径、浅覆土始发引起的地表沉降规律、沉降槽分布形式及其影响范围、沉降随时间发展规律、沉降量概率分布的统计分析等.上述关于浅埋隧道施工问题的研究工作大多是对施工参数以及监测试验数据的统计分析为主.

本研究以国内首次应用URUP法隧道施工方法的南京机场城轨隧道示范工程为背景,对URUP法隧道施工过程进行了三维非线性数值模拟,主要针对超浅覆土和负覆土区间隧道施工过程的地表变形规律以及施工影响范围进行相关预测,分析了盾构掘进过程中超浅覆土和负覆土区间地表变形的特点,以期对工程实施起到一定的指导作用.

1 工程概况

1.1 工程背景

如图2所示,南京机场城际快速轨道位于将军路站至秣陵站之间的隧道,由地下段和地上段组成,符合URUP法隧道新技术实施的需要.因此,将该区段作为URUP法隧道示范工程.本研究即是对该示范工程自地下段至地上段区间施工过程的地表沉降及其影响范围进行预测分析.

1.2 地质条件

根据地质勘测资料,本工程沿线地层分布从上到下的次序如下:①-2层压实填土,厚度一般在1.2～5.2m,工程地质性能一般;下伏④-1b1粉质粘土,硬塑,中压缩性,工程地质性能较好;坳沟段上部分布②-1b2层粉质粘土,可塑为主,局部硬塑状态,强度中等,工程地质性能较好;②-3c1-2层粉土,湿,密实状态,局部中密,强度中等,工程地质性能一般;下部分布④-1b1.基底主要为侏罗系龙王山组安山岩:J3l-1全风化安山岩,风化强烈,砂土状夹碎块状,局部粘土化,工程地质性能变化较大,土质一般;J3l-2强风化安山岩,岩芯呈块状,工程地质性能较好;J3l-3中风化安山岩,岩芯呈柱状,工程地质性能好.图3为本工程隧道纵断地质剖面图.各岩土层具体的物理力学性能参数如表1所示.

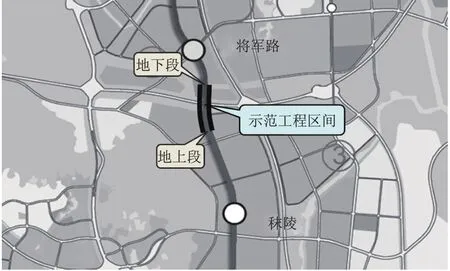
图2 示范工程地理位置示意图Fig.2 Schematic diagram of the geographical position of the demonstration project

图3 隧道纵断地质剖面图Fig.3 Longitudinal geologic section of tunnel

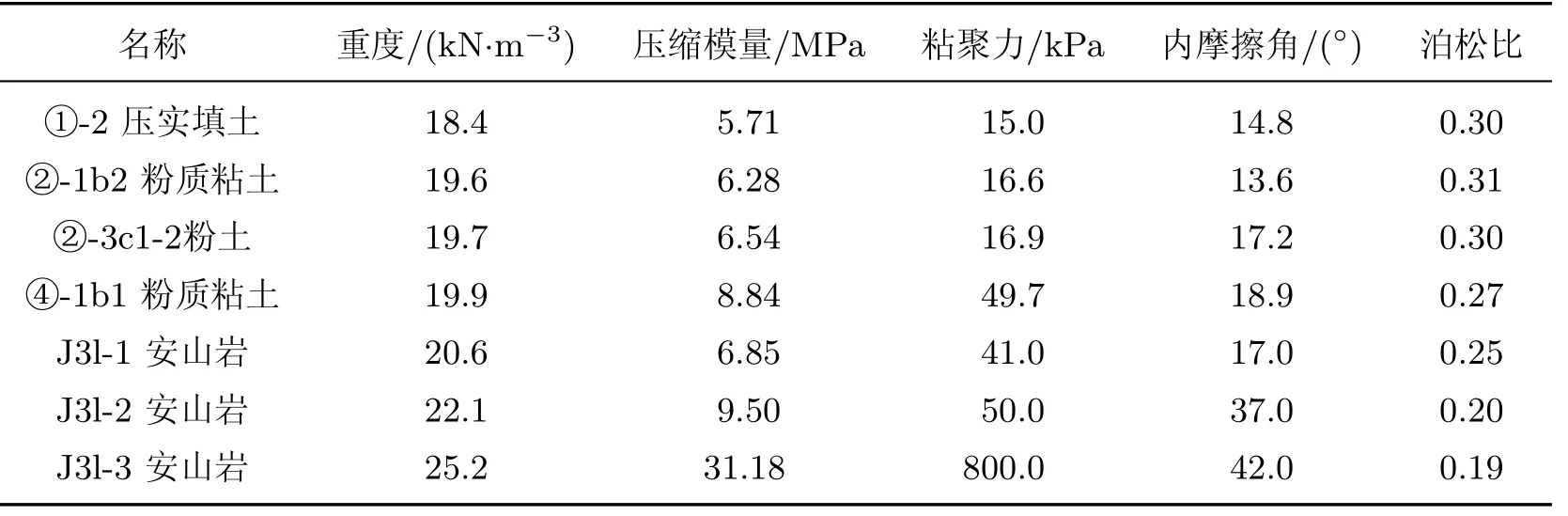
表1 岩土层的基本物理力学参数Table 1 Physical and mechanical parameters of strata

2 有限元模型及模拟方法

2.1 模型建立及参数拟定

示范工程采用自主研发的土压平衡式盾构机.盾构机长为7.92m,盾壳外径为6.34 m,盾壳厚为7 cm,刀盘外径(切削直径)为6.38 m.衬砌采用预制钢筋混凝土管片,混凝土强度等级为C50,管片环外径为6.2 m,内径为5.5 m,管片宽为1.2 m,厚为0.35 m.模型中盾壳、衬砌单元均采用线弹性材料本构,相应的力学指标如表2所示.

由图3所示的隧道纵断地质剖面图可见,示范工程沿线所处的岩土层竖向分布不均匀,因此,本研究建立了接近真实岩土层分布环境的三维有限元模型,使数值模拟过程更接近真实工况.图4为用Abaqus软件建立的有限元模型.

表2 盾壳、衬砌模型的物理力学参数Table 2 Physical and mechanical parameters of shield and lining

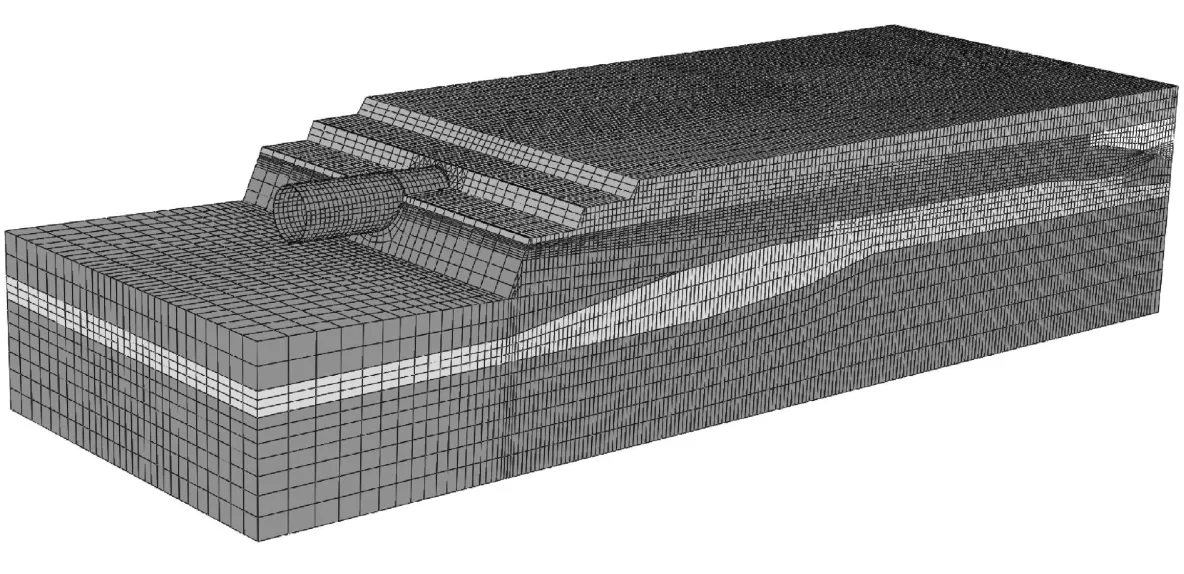
图4 地层分布及三维有限元网格图Fig.4 Strata distribution and 3D FEM mesh

该模型尺寸沿隧道纵轴向(x轴方向)长为150 m,隧道横轴向(z轴方向)为60 m,竖向(y轴方向)为30m.模型共有230687个单元,节点总数为249392,其中线性六面体非协调模式单元(C3D8I)228 542个,放坡面局部采用二次四面体修正单元(C3D10M)2 145个.

计算模型的边界条件如下:上表面取为自由边界,侧面限制水平方向移动,放坡面无位移约束条件;底部固定;根据实际工况,盾构在出洞段部分,在盾壳单元底部限制其竖向位移.

模型中岩土体的力学性能指标如表1所示.与盾壳、衬砌单元不同的是,岩土体是典型的“摩阻”型材料,其强度与所处的压力状态具有非常密切的关系.因此,在盾构稳态掘进的数值模型中,土体采用弹塑性材料本构,其屈服准则服从Drucker-Prager准则.

在数值模拟过程中,将一些与施工过程密切相关但又不易量化的变量(如盾尾空隙大小、注浆充填程度、隧道壁面土体受扰动的程度和范围等)概化为均质、等厚的等代层.用等代层替换衬砌周围实际的土层能较客观地反映这些不易量化的因素对地表位移的综合影响.具体方法如下:在衬砌结构周边采用均质、等厚、弹性的等代层替换衬砌周围实际的土层,让其产生的地表沉降等效于考虑盾尾空隙、土体向盾尾空隙的自然充填和隧道壁面受扰动等多种施工因素造成的地表沉降,从而使一些不易量化的因素在计算模型中得以实现.等代层按线弹性材料计算,其参数根据张云等[22]的反分析结果,结合地层特性、隧道管径和注浆情况等因素综合确定.模型中等代层的物理力学参数如表3所示.

表3 等代层的物理力学参数Table 3 Physical and mechanical parameters of equivalent layer

2.2 URUP法隧道施工过程的三维有限元模拟方法

考虑到超浅覆土、负覆土下盾构掘进施工对土体扰动效应增大,URUP法隧道施工过程的数值模拟共采用如下6个步骤.

(1)初始地应力的计算与平衡.首先,“杀死”盾构、管片、等代层单元,仅就土体单独施加重力,计算初始地应力场.然后,将初始地应力场施加于模型,进行地应力平衡.由于本工程有限元模型较复杂,土层分布不规则,初始地应力平衡采用导入地应力场文件的方法进行.

(2)施加开挖面压力,对欲开挖土体进行应力释放.刀盘前方欲开挖土体由于受到刀盘的推力和扭矩作用,土体受扰动后应力释放.考虑到盾构在超浅覆土、负覆土工况下掘进施工对土体扰动效应增大的特点,模拟过程在对欲开挖土体单元进行刚度折减的同时再进行一定的密度折减.

(3)土体开挖,“杀死”开挖土体,同时激活盾构单元.“杀死”刀盘前方欲开挖土体,同时激活相应盾构单元,施加开挖面土仓压力和盾壳与土体的相互作用.盾壳与土体的相互作用采用硬接触模拟.

(4)管片安装,“杀死”盾尾盾构单元,同时激活衬砌(管片)单元和初始等代层,施加盾尾注浆压力.模拟注浆效果对盾尾空隙的填充作用.

(5)等代层硬化.改变初始等代层的单元材料属性为凝结硬化,同时卸载盾尾注浆压力.

(6)循环步骤(2)～步骤(5).

计算步长采取每步长向前掘进一个衬砌(管片)单元的宽度(1.2 m),模拟过程为盾构从始发位置(第1环)掘进至到达地表(盾构推进至第90环)再到第90环等代层凝结硬化(盾构推进至第99环,盾尾共92环管片),共计计算载荷步191步.由于在盾构实际施工时,盾尾注浆硬化需要一定的时间,因此本工程在数值模拟时假定管片脱出盾尾2环以后,注浆硬化完成,开挖面压力及盾尾注浆压力采用面荷载施加到相应的单元面上.整个数值模拟计算过程利用Abaqus有限元分析软件进行.

2.3 非线性计算

为了预测URUP法示范工程安全稳定的施工过程,本研究模拟计算了采用稳定平衡的开挖面土压力进行整个施工过程的开挖,计算中同时施加重力、盾壳与土体的摩擦力及盾尾注浆压力.

在每一个计算载荷步中建立如下的非线性有限元求解方程:

式中,Kep(a)为弹塑性刚度矩阵,a为位移向量,Δa为位移增量向量,ΔQ为载荷增量向量.

采用Newton-Raphson迭代方法求解方程(1).计算时将载荷向量P分为若干个微小增量ΔP,对于结构每次受到的一个微小载荷增量ΔP,已知初始结构位移为a0,初始结构载荷为P0,结构载荷P1=P0+ΔP.令a=a0,ΔQ=ΔP,代入方程(1)可计算出关于结构在这一步增量后的位移修正值Δa0:

于是得到第一次近似解a1=a0+Δa0,定义残差值为

令a=a1,ΔQ=R1,代入方程(1)～(3)即可得到修正值Δa1、第二次近似解a2及残差值R2.重复上述迭代,可得到第n次近似解an及残差值Rn:

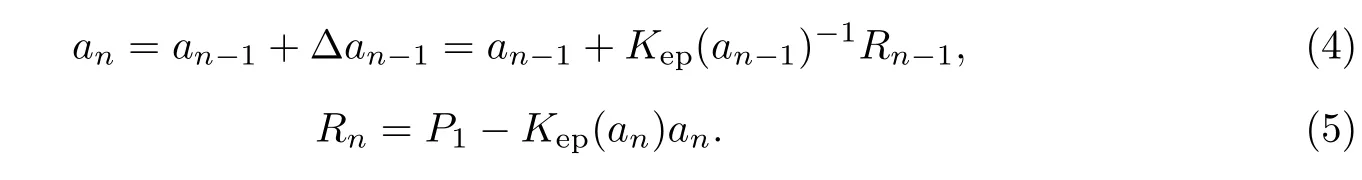
3 模型可靠性验证

考虑到地表沉降不会在盾构开挖后立即稳定,以盾构掘进40环以内的地表沉降计算结果进行模型验证,将模拟计算结果与施工中布设的相应沉降监测点的采集数据进行对比.施工中的纵向沉降监测点由始发端每3环(间距3.6 m)位置布设一个.相应地,在若干纵向监测点位置处垂直于隧道轴线方向布置横向监测点,横向监测点大致对称地布置在轴线两侧,每隔2～3 m布设一个.

盾构掘进完成40环(48 m)后,隧道纵断面的沉降分布云图如图5所示,模型模拟计算的地表沉降数据与实测值的比较如图6所示.

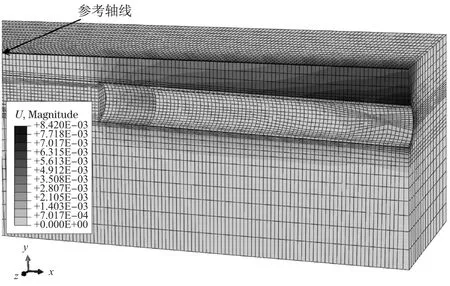
图5 掘进至第40环(48m)时,距离地层竖向的位移分布云图Fig.5 Vertical ground contour displacement when excavated to the 40th ring(48m)

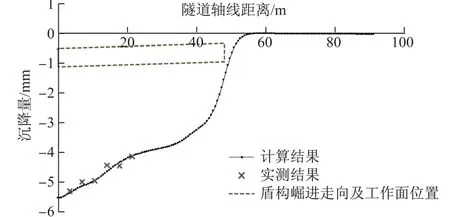
图6 掘进至第40环(48 m)时,隧道轴线纵向地表沉降曲线与已有监测值的比较Fig.6 Comparison between simulated longitudinal subsidence curve and monitoring data of the ground surface when excavated to the 40th ring(48 m)

由于距工作面后方25 m位置处的地表沉降基本趋于稳定,图6中自始发位置(坐标原点)至隧道轴线距离23 m之间的曲线分布可视为隧道纵轴线稳定的地表沉降曲线.可以看出,盾构机在该区段正常掘进时,模型模拟的计算结果与实测数据较为接近,计算所得的地表稳定沉降值与实测数据也基本相吻合.

图7分别给出了第15和33环横断面地表沉降分布数值模拟计算结果与实测数据的对比结果.可以看出,横断面中心处地表累计沉降值最大,切口上方两侧有轻微隆起,沉降量、隆起量沿隧道中心线呈对称分布,沉降主要分布在距轴线两侧各10 m范围内,距轴线15 m以外区域几乎不受影响.模型模拟计算所得横向沉降区域与实测沉降范围比较接近,累计沉降最大值的计算结果与实测结果也吻合得较好.

图7 横向沉降计算值与监测值的比较Fig.7 Comparison between simulated transverse settlements and monitoring data of the ground surface

综上,通过比较模型模拟计算得到的隧道纵、横断面地表沉降曲线与实测的沉降数据发现,计算结果较好地吻合了盾构隧道施工所造成的实测地表沉降.这表明本研究所建立的针对URUP法隧道施工的三维非线性有限元模型及模拟计算方法是有效可行的,由此所得出的预测计算结果也是合理可信的.

4 预测分析

4.1 地表沉降预测分析

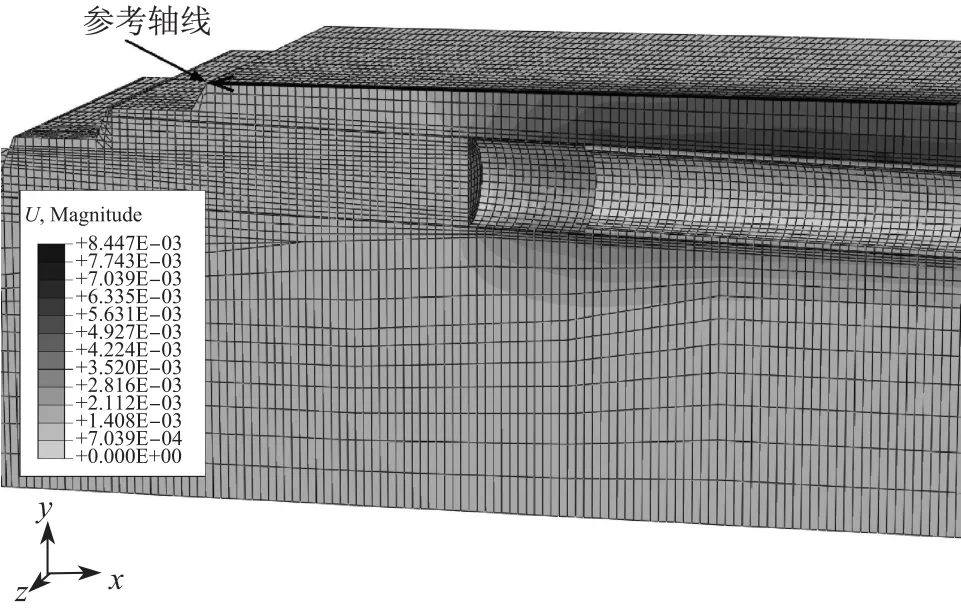
图8 掘进至第60环(72 m)位置时的地层位移云图Fig.8 Ground contour displacement when excavated to the 60th ring(72 m)

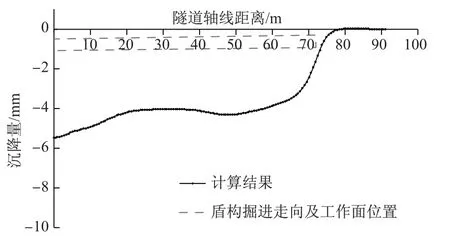
图9 掘进至第60环(72 m)位置时,隧道轴线上方纵向地表沉降位移曲线Fig.9 Simulated longitudinal subsidence curve of the ground surface when excavated to the 60th ring(72 m)

图8为盾构机掘进至第60环(72 m)位置处,隧道纵断面地层位移云图.图9为模拟计算开挖至第60环(72 m)位置处,隧道轴线上方纵向地表沉降计算结果.此时盾构掘进至隧道覆土厚度约0.5D处.总体来看,地表沉降不明显.此后,盾构掘进将进入超浅覆土区间.

图9所示为盾构出洞后地层沉降稳定(最后一环等代层单元硬化)时,隧道轴线上方纵向地表沉降数值计算结果.由于盾构机于90 m附近位置处已掘出地表,故后续负覆土掘进区间无地表沉降的计算结果.

从图9和10中隧道轴线上方地表沉降计算结果可以看出,盾构机在正常掘进过程和隧道整体施工完毕后所引起的地表沉降量基本控制在2～6 mm之间,沉降值较小主要与盾构掘进过程所经历的岩土层(粉质粘土、粉土和全风化安山岩等)工程地质性能较好有关.距盾构始发端15～40 m位置区间范围内的地表沉降值比较小(见图9,该段曲线呈轻微隆起状),其原因主要是因为盾构机于该区间掘进所经历的土层主要为工程地质性能较好的粉质粘土和安山岩(见图3),因此其沉降值较其他位置小.盾构始发阶段15 m范围内的地表沉降量较大,最大值出现在盾构始发位置处,约为5.5 mm.

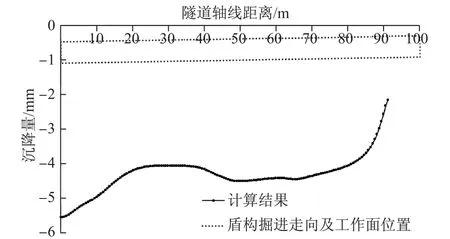
图10 隧道轴线上方纵向地表最终稳定沉降位移曲线Fig.10 Simulated longitudinal subsidence curve of the ground surface when eventually stabilized

4.2 超浅覆土区间沉降变化规律预测分析

本研究将超浅覆土掘进区段模拟过程第79环(覆土厚度约为0.1D)位置处的断面作为预测基准面,分析了该超浅覆土区段数值模拟的沉降结果随时间发展的差异.将示范工程的深埋掘进区段第15环(覆土厚度约为0.75D)位置处的断面作为参考断面,分析对比了超浅覆土(见图11(a))与深埋覆土(见图11(b))隧道施工沉降随时间发展规律的异同.

图11中的横坐标代表计算点到开挖面的距离.当基准面为开挖面时位于图中横坐标0处.图中自右向左从正值减少到0表示盾构机开挖面与基准面距离逐渐接近;从0减少到负值则表示盾构通过并逐渐远离基准面.

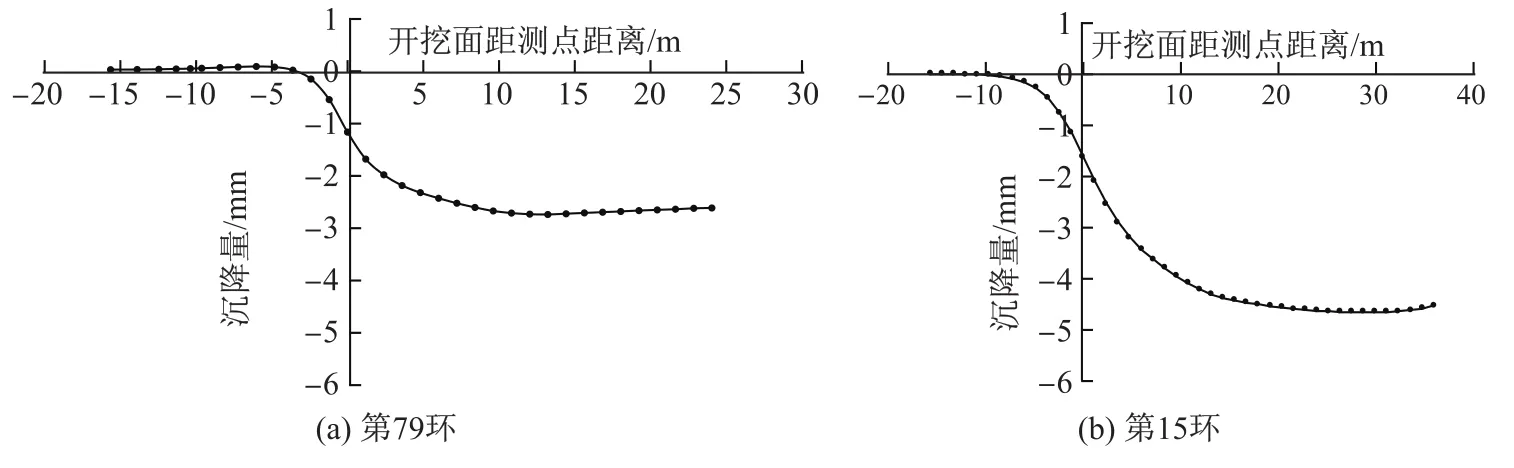
图11 隧道开挖过程中不同位置处的地表沉降计算结果Fig.11 Simulated subsidence curves of the ground surface during tunnel excavation

从图11(a)的数据结果可以看出:超浅覆土下掘进对纵向地表的显著影响区域为刀盘前方10 m至盾构刀盘后方20 m左右位置区间,其间沉降量约占总沉降量的90%以上;刀盘后方20 m位置处沉降基本趋于稳定,最大累计沉降值在3 mm以内.参考图11(a)中断面沉降量计算结果随时间的发展过程可以看出,变化过程可大体分为如下3个阶段.

(1)轻微隆起,可由图中盾构机开挖面前方约4～10 m之间地表所产生的轻微隆起得到.该阶段的隆起发展趋势总体表现为由距基准面较远处的变化缓慢到临近5m处的快速发展,其中开挖面前方隆起约0.1 mm.该阶段所产生的隆起主要是由盾构掘进推力与开挖面前方土压力失衡所致.

(2)盾构通过沉降,可由图中盾构机刀盘至盾尾整体通过基准断面前后沉降差值约为2.5 mm的结果得到.该阶段的沉降发展趋势总体表现为快速增长.该阶段所产生的沉降主要是盾构掘进过程对土体的扰动,以及由于盾构的刀盘外径(切削直径)往往稍大于盾壳直径所引起的地层损失使土体应力释放所致.

(3)盾尾空隙沉降,可由图中盾尾通过基准断面之后所引起的约0.5 mm的沉降量结果得到.该阶段的沉降发展趋势总体表现为由盾尾后方附近沉降值的快速增长到距盾尾后方约10 m处的沉降发展变化减缓,并逐渐趋于稳定.该阶段所产生的沉降主要是盾构尾部的建筑空隙致使其周围土体应力释放引起土体产生弹塑性变形所致.

从以上隧道沉降随时间发展规律的有限元计算结果可以看出,超浅覆土区间由盾构掘进引起前方土体卸荷导致的地面沉降量占地表最大沉降量的30%左右,大部分地面沉降是由盾构通过以及盾尾后的建筑空隙引起的.开挖面后方地表沉降随盾构推进开挖面距离的增加逐渐趋于稳定,在盾构开挖面后方约20 m的位置,地层沉降基本趋于稳定.

根据上述计算结果,在总结和分析超浅覆土隧道施工引发地面沉降规律的基础上,对比了示范工程的深埋覆土隧道施工情况,分析了二者沉降规律的异同.

从图11(b)中的计算数据结果可以看出,示范工程的深埋覆土下盾构掘进的纵向主要影响区域为刀盘前方15 m至盾构刀盘后方30 m,其中显著影响区域为刀盘前方10 m左右至盾构刀盘后方20 m左右位置区间,其间沉降量约占总沉降量的90%以上.刀盘后方25 m位置处沉降基本趋于稳定,最大累计沉降量在5 mm以内.从参考断面沉降量计算结果随时间的发展过程可以看出,盾构于深埋覆土区段掘进其纵向地表沉降过程(见图11(b),覆土厚度约为0.75D)与盾构于超浅覆土(见图11(a),覆土厚度约为0.1D)的发展趋势及速率大体一致,整个过程亦可分为3个阶段,分别为开挖面前方沉降(或隆起)阶段、盾构通过沉降阶段和盾尾空隙沉降阶段.

综上可以得到,除地表沉降量、纵向地表的显著影响区域以及盾尾后方的沉降稳定距离不同外,盾构超浅覆土掘进与盾构深埋覆土掘进地表纵向沉降发展趋势及速率基本一致,整个过程均可分为3个阶段:开挖面前方沉降(或隆起)阶段、盾构通过沉降阶段和盾尾空隙沉降阶段.

4.3 负覆土区间影响范围预测分析

将负覆土掘进区段模拟过程第85和87环(覆土厚度约为—0.3D)断面位置作为预测基准面.由于在负覆土工况下,盾构机与衬砌结构部分已掘出地表,故在负覆土区间以沉降稳定时数值模拟计算得到的地表横断面沉降曲线分布结果进行施工影响范围的预测分析(见图12).

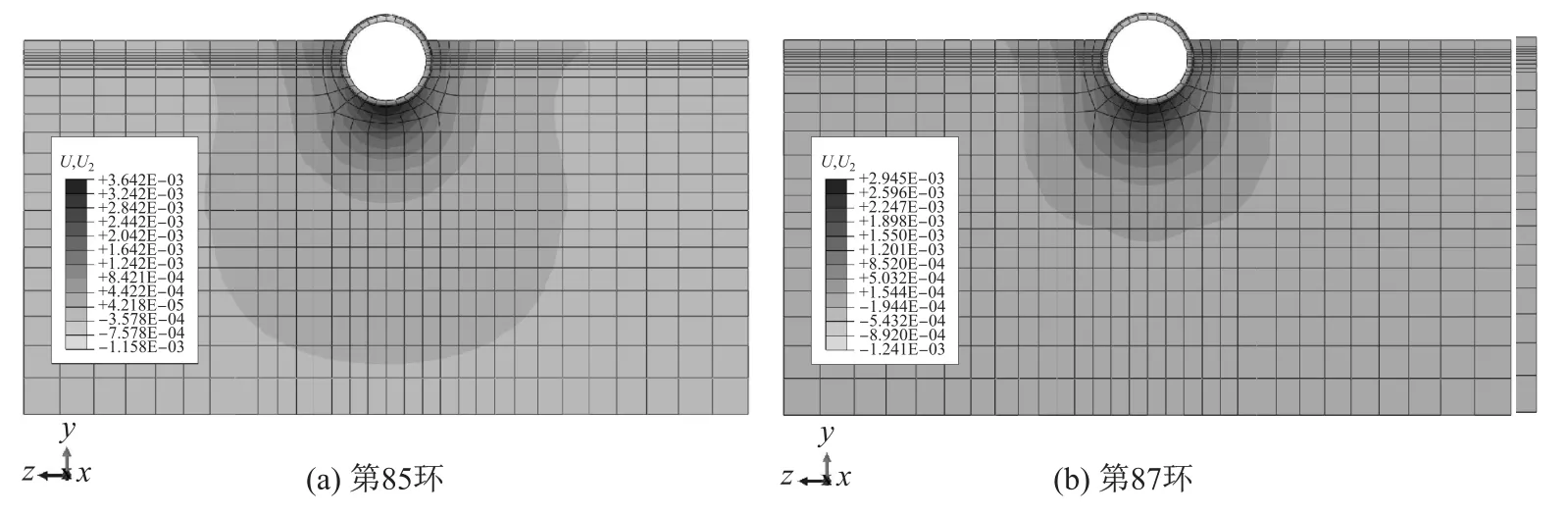
图12 横断面地层竖向位移分布云图Fig.12 Vertical ground contour displacement

图13分别为第85和87环(覆土厚度约为—0.3D)断面位置处变形稳定后的横断面地表隆沉有限元计算结果.可以看出,横断面隆沉曲线在临近衬砌位置处的地表轻微隆起,隆起量在1.2 mm左右;在衬砌位置与距隧道轴线约10 m范围内沉降值急剧减小而后曲线趋于平缓;在远离隧道轴线,距隧道轴线约15 m以外地表基本无隆沉.因此,负覆土区间盾构施工引起的土体变形规律为临近衬砌位置处地表出现轻微隆起,隆起量沿着隧道中心线呈对称分布,隆起范围主要分布在距隧道轴线两侧各15 m范围内,距隧道轴线15 m以外区域几乎不受影响.

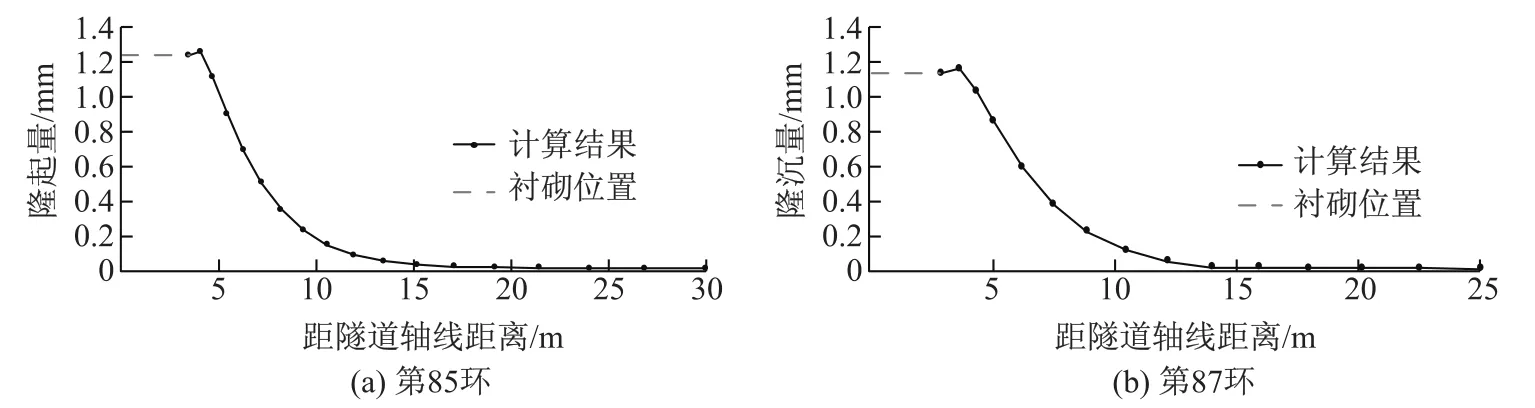
图13 横向隆沉计算值Fig.13 Simulated transverse settlements of the ground surface

5 结论

(1)本研究以国内首个URUP法隧道施工技术的实际工程为背景,对URUP法隧道施工过程进行了有限元建模与数值模拟,预测了超浅覆土和负覆土区间盾构法隧道施工过程的地表变形规律以及施工影响范围.

(2)基于三维非线性有限元数值计算,预测了示范工程的地表沉降结果.由于盾构掘进区间的岩土层工程地质性能较好,最终的地表沉降量并不大,最大沉降出现在盾构始发段.

(3)预测分析了超浅覆土区段掘进其纵向地表沉降随时间的发展过程,可分为3个阶段:开挖面前方隆起阶段、盾构通过沉降阶段和盾尾空隙沉降阶段.超浅覆土区段以稳定平衡土压掘进的纵向显著影响区域为刀盘前方10 m左右至盾构刀盘后方20 m左右位置区间,其间沉降量约占总沉降量的90%以上,刀盘后方20 m位置处沉降基本趋于稳定.

(4)预测了负覆土区段以稳定平衡土压掘进时,盾构施工的影响范围分布在距轴线两侧各15 m范围内,距轴线15 m以外区域几乎不受影响.

(5)比较了地表沉降的计算结果与实测数据,发现计算结果较好地吻合了盾构隧道施工实测结果.这说明本研究所采用的三维有限元模型及模拟方法能够很好地模拟URUP法隧道掘进施工对土体变形的影响,验证了示范工程预测分析结果的有效性和可信性.

[1]TOSHIO T,KINSAKU K,KEIZO M.Construction of MRT chaloem ratchamongkhon line underground structures north and Japanese shield tunnel technology[C]//Proceedings of International Symposium on Underground Excavation and Tunneling.2006:47-56．

[2]KEIZO M,FUMIYUKI Y,HIROSHI U,et al.Development of construction method for a road underpass at intersection[C]//Proceedings of 2009 World Tunnel Congress.2009:31-35．

[3]BRIjER A J.Ultra rapid under pass: the adaptation of the URUP method for the Netherlands[D].Delft:Delft University of Technology,2010．

[4]HITONARI F,TETSUYA N,MASAYOSHI I.URUP(ultra rapid under pass)method,the fi rst shield tunneling method for launching and arrival at the ground level[C]//Proceedings of 2009 World Tunnel Congress.2009:112-116．

[5]TOSHIAKI N,KENjI K.URUP(ultra rapid under pass)method,the fi rst implementation in a public project[C]//Proceedings of 1st International Congress on Tunnels and Underground Structures in South-East Europe.2010:1175-1180．

[6]YAMAUCHI K,TANAKA Y,NONAKA T.URUP(ultra rapid under pass)-TBM excavation in soft ground from the surface elevation(zero overburden)without shaft and/or large scaled open cut pit[C]//Proceedings of 2011 Rapid Excavation and Tunneling Conference,Society for Mining, Metallurgy and Exploration.2011:946-963．

[7]张子新,胡文．地面出入式盾构法隧道新技术大型模型试验与工程应用研究[J]．岩石力学与工程学报,2013,32(11):2161-2169．

[8]LEE K M,ROWE R K.Finite element modeling of the three-dimensional ground deformations due to tunneling in soft cohesive soils:partⅠ—methods of analysis[J].Computers and Geotechnics,1990,2(2):87-110．

[9]LEE K M,ROWE R K.Finite element modeling of the three-dimensional ground deformations due to tunneling in soft cohesive soils:partⅡ—results[J].Computers and Geotechnics,1990, 2(2):111-138．

[10]王敏强,陈胜宏．盾构推进隧道结构三维非线性有限元仿真[J]．岩石力学与工程学报,2002,21(2): 228-232．

[11]张利民,李大勇．盾构掘进过程土体变形特性数值模拟[J]．岩土力学,2004,25(S1):75-78．

[12]张海波,殷宗泽,朱俊高．地铁隧道盾构法施工过程中地层变位的三维有限元模拟[J]．岩石力学与工程学报,2005,24(5):755-760．

[13]李曙光,方理刚,赵丹．盾构法地铁隧道施工引起的地表变形分析[J]．中国铁道科学,2006,27(5): 87-92．

[14]朱合华,丁文其,桥本正．盾构隧道施工过程模拟分析[J]．岩石力学与工程学报,1999,18(S1): 860-864．

[15]朱合华,丁文其,李晓军．盾构隧道施工力学性态模拟及工程应用[J]．土木工程学报,2000,33(3): 98-103．

[16]尚国庆,冯伟．超大型泥水平衡盾构施工的三维非线性模拟[J]．上海大学学报:自然科学版,2009, 15(5):541-545．

[17]宁寅,冯伟,马永其,等．下穿已有隧道泥水盾构施工的预测分析[J]．上海大学学报:自然科学版, 2012,18(4):401-407．

[18]朱合华,刘庭金．超浅埋盾构法隧道施工方案三维有限元分析[J]．现代隧道技术,2001,38(6): 14-18．

[19]张所明,张国跃,洪庄年,等．浅覆土大盾构对临近建筑物影响的有限元分析[J]．工程地质学报, 2008,16(S1):108-110．

[20]吴惠明,汤漩．上海轨道交通9号线超浅覆土盾构施工引起的地面变形特性及对策[C]//地下工程建设与环境和谐发展—–第四届中国国际隧道工程研讨会文集．2009:122-129．

[21]陈林．地铁出入段线盾构隧道区间—–浅覆土、小半径始发地面沉降规律分析[C]//地下交通工程与工程安全—–第五届中国国际隧道工程研讨会文集．2011:540-544．

[22]张云,殷宗泽,徐永福．盾构法隧道引起的地表变形分析[J]．岩石力学与工程学报,2002,21(3): 388-392．

本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn

Predictive analysis on shield tunnel using ultra-rapid under pass method

ZHAO Xin-wei1,MA Yong-qi1,2,TENG Li3
(1.Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University, Shanghai 200072,China; 2.College of Sciences,Shanghai University,Shanghai 200444,China; 3.Shanghai Urban Construction Co.,Ltd.,Shanghai 200122,China)

Ultra-rapid under pass(URUP)is a new shield construction method.The shield machine directly excavate from surface of the beginning section to the surface of the target location.Based on the demonstration project of Nanjing shield tunnel using the URUP method,the whole shield construction process is simulated with a three dimensional nonlinear fi nite element method(FEM).The ground surface subsidence,the a ff ected area, and the fi nal settlement of ultra-thin ground coverage and partially out of the ground in the shield process are predicted and analyzed.Comparison with the measured data shows that the calculation is reliable.The results provide useful guidance to the project,and may be used as a reference for analysis of similar projects.

predictive analysis;ultra-rapid under pass(URUP)method;3D fi nit element method(FEM)simulation;ground surface settlements

TU 447

A

1007-2861(2015)04-0454-13

10.3969/j.issn.1007-2861.2014.01.040

2014-02-26

上海市科委基金资助项目(11231202700)

马永其(1966—),男,博士,副教授,研究方向为地下工程及相关力学.E-mail:mayq@sta ff.shu.edu.cn