粘接材料及结构在双轴受压和温度耦合作用下变形的尺度效应和非局部效应分析

刘 亮,彭香武,王青占,郭兴明

(上海大学上海市应用数学和力学研究所,上海 200072)

粘接材料及结构在双轴受压和温度耦合作用下变形的尺度效应和非局部效应分析

刘 亮,彭香武,王青占,郭兴明

(上海大学上海市应用数学和力学研究所,上海 200072)

基于非局部理论,分析了双层完好粘接板在双轴受压和温度场耦合作用下屈曲的尺度效应和非局部效应.通过理论计算对经典弹性理论和非局部理论的计算结果进行了比较分析.结果表明:在非局部理论下,由于系统内部结构之间的相互作用,系统的屈曲临界力有所降低,并且当屈曲波数越大时,内部结构相互作用域进一步收缩,使得有效弯曲刚度减小,所以非局部参数对屈曲力的影响更为显著;在外载荷和温度耦合作用下,温度升高会导致屈曲临界力减小,温度降低会导致屈曲临界力增大.还对3种不同温度场进行了讨论,分析了在3种温度场下温度变化对外载荷的影响,以及与系统尺寸大小的关系.

非局部理论;粘接材料;屈曲;双轴受压;温度变化

随着电子产业和建筑业的迅速发展,为了满足特定的工业性能以及材料和结构的加固修复等需要,粘接材料也得到了充分的应用.因为粘接材料内的应力和应变传递与传统的机械紧固相比分布更加均匀,且粘接材料和结构具有强度高、成本低、质量轻和外表光滑等优势,所以粘接材料在很多领域得到了充分利用,如桥梁的加固、电子元件、宇航器件粘接减轻质量等.对粘接问题的研究也较多,例如Chen等[1]对弹性基体上粘接的薄膜屈曲问题进行了讨论,分析了人字形屈曲模型的原理.Huang等[2-4]分析了弹性基体、粘弹性基体和粘性基体上粘接薄膜的屈曲问题,讨论了不同基体下能量和动力学对起皱临界条件的影响.Li等[5]则通过建立三维模型,对粘接薄膜的屈曲和后屈曲进行了研究.

随着制造业的蓬勃发展,工业器件的尺寸也逐渐变小,这样可以减小体积、减轻质量,方便日常的携带使用,但由此也带来了一些客观问题,如微电子材料的力学行为和细微力学等.经典的连续介质力学把物体看成均匀的连续介质,运用场的概念来描述物质的运动,而且局限于在宏观范畴内应用.随着新材料的快速发展和高端技术的运用,出现了许多用经典理论不能解决的实际问题.不论什么物质都有其自身特定的内部结构.这些结构通过原子间的相互作用或者介质的传递,彼此间存在一定的影响.无论内部的相互作用是哪种尺度上的,对于特定的物质,都存在一个对应的内部特征尺度.当内部特征尺度和外部特征尺度相近时,内部结构对外载荷作用的影响就显得尤为重要.这时,经典理论就不能精确地解决实际问题,需要寻求新的解决方法.Eringen[6-8]建立了系统的非局部理论.因为非局部理论既有经典连续介质理论的基础,又精确表达了物质内部的相互作用,所以在许多问题中得到了应用,尤其在断裂问题和小尺度材料的力学分析等方面.Shen[9]利用非局部理论对基体上薄膜进行了非线性分析.Bazant等[10-11]基于非局部理论对材料的断裂损伤和屈服极限等问题进行了研究分析.Pradhan等[12-14]对弹性基体上单层石墨烯或者纳米板的单轴、双轴压缩屈曲及其振动进行了研究.Wang等[15]运用非局部理论对微纳尺度结构做了静态分析.Samaei等[16]利用非局部Mindlin板理论分析了弹性基体中单层石墨烯的屈曲问题.Aghababaei等[17]在板的高阶剪切非局部理论下研究了纳米板的线性屈曲和振动的非局部效应.Arash等[18]在已有结果的基础上对非局部理论在微纳尺度材料上的应用做了总结.Narendar[19]通过板的一阶剪切变形理论分析了非局部理论下微纳尺度板的屈曲问题.此外,在现代的机械制造、航空航天、冶金建筑等国防和民用工业领域中,热应力和热屈曲现象普遍存在.器件在工作期间由于摩擦导致温度的改变会引起热应力的产生.这对器件的强度安全和使用寿命都会产生很大影响,因此结构的热屈曲分析一直都备受关注.在小尺度材料中,Hao等[20]在分析多壁碳纳米管的扭转屈曲时就考虑了温度对其结果的影响.结果表明,温度升高(降低)时会导致屈曲力减小(增大). Wang等[21]讨论了非局部参数影响下纳米板的热屈曲问题.Kumar等[22]分析了弹性基体中多层石墨烯的热振动问题,温度对材料的稳定性影响得到了广泛的关注.

本工作从双层完好粘接板模型出发,基于非局部理论,对模型在双轴受压和温度耦合作用下的屈曲稳定性以及相关的尺度效应进行了研究讨论.结果表明,非局部参数对屈曲力的影响比较显著,尤其当屈曲波数较大时,非局部参数对屈曲力的影响更加显著,不可忽略;同时得到了温度变化对屈曲力的影响关系.分别讨论了在3种不同温度场下温差对外载屈曲力的影响.本工作所得到的结果将对相关工业器件的强度设计和安全监测提供很大的参考价值.

1 模型及控制方程的建立

如图1所示,双层完好粘接板由不同材质的各向同性材料组成,上下板的厚度分别为h1和h2,弹性模量分别为E1和E2,泊松比分别为ν1和ν2,模型的长为a,宽为b,板在双轴受到的轴向压力分别为Nx1,Ny1,Nx2,Ny2.在发生屈曲前上下板保持完好粘接,不发生脱粘.

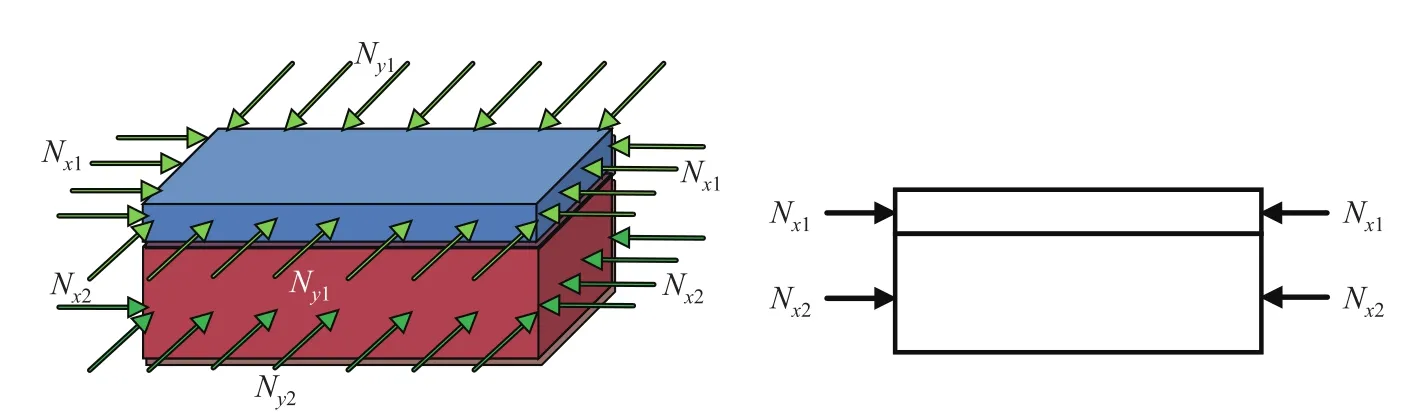
图1 双层粘接板双轴受压模型Fig.1 Double layer bonding plates under both biaxial compression

基于Eringen[6]的非局部弹性理论,连续弹性介质中某一参考点的应力不仅仅取决于这一点的应变,同时还受到相连应变域内各点对其的影响.在非局部理论中,模型内部尺寸被当作特定的材料参数,因此最通常形式的非局部理论下的本构关系涉及一个整体的积分.在忽略体重之后,有线性均匀的非局部弹性体的基本方程为

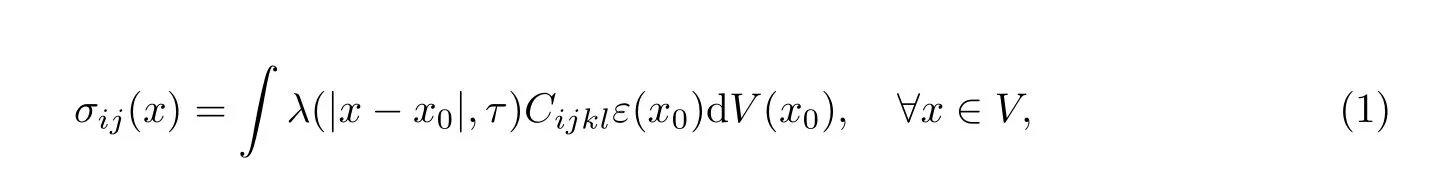
式中,σij为参考点的应力,Cijkl为四阶应力张量,λ(|x-x0|,τ)为非局部系数(或者称为本构方程的衰减函数,表示非局部理论下,x0点对参考点x的影响),|x-x0|为欧氏空间下两点的距离,τ=e0a/l为材料参数(由内部和外部的特征长度决定,其中比较关键的参数e0可以通过非局部理论计算值和分子动力学结果推算得到),a和l分别为内部和外部特征长度.对于线性各向同性材料,式(1)可以简化为如下的应力应变关系:

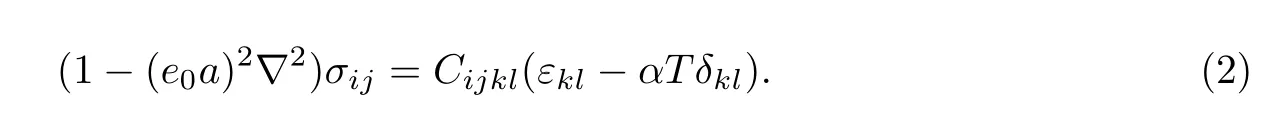
二维的双层粘接板的非局部本构方程为

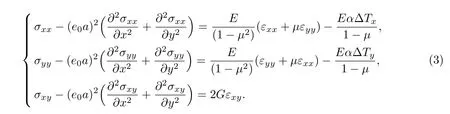
由应力可得外载荷和弯矩的表达式为

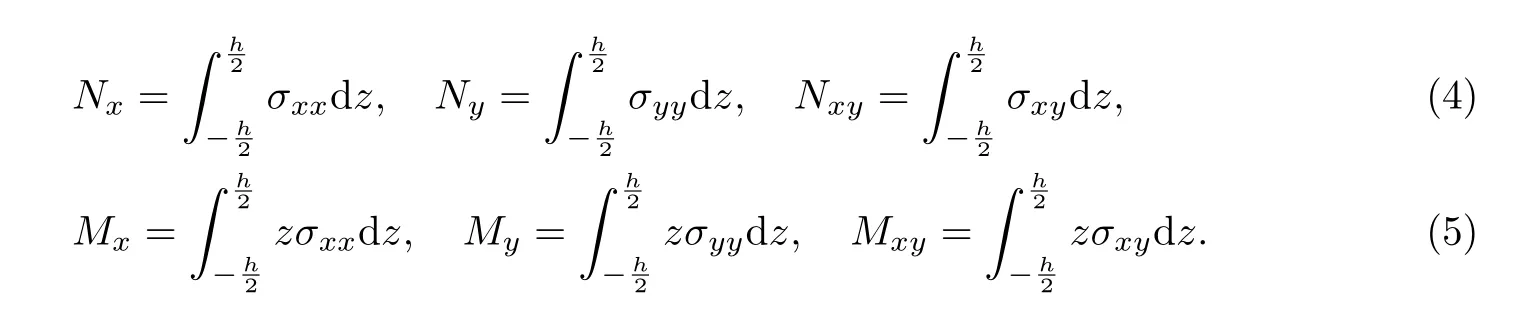
在非局部理论下,非局部参数的确定至关重要,而非局部参数与材料内部相互作用的尺度相关联,且非局部参数的量纲为长度的平方.在控制方程(14)下,本工作设定模型材料参数时所取的模型尺寸为无量纲下的尺寸.假设b=10,h2=1,µ=0.4,本工作对双轴受压和温度耦合作用下的系统的临界屈曲波数进行了讨论分析.可以发现,在均匀温度场中,当ΔT=100K, Γ=5,ξ=0.1,Λ=10,ψ=1,δ=1,e0a=1.0时,随着屈曲波数m,n的增大,所需的屈曲外载荷也逐渐变大;当波数m=n=1时,所需的屈曲外载荷的值最小,即为屈曲临界值(见图2).在讨论温度场变化对屈曲力的影响时,取屈曲临界波数m=n=1进行计算分析.

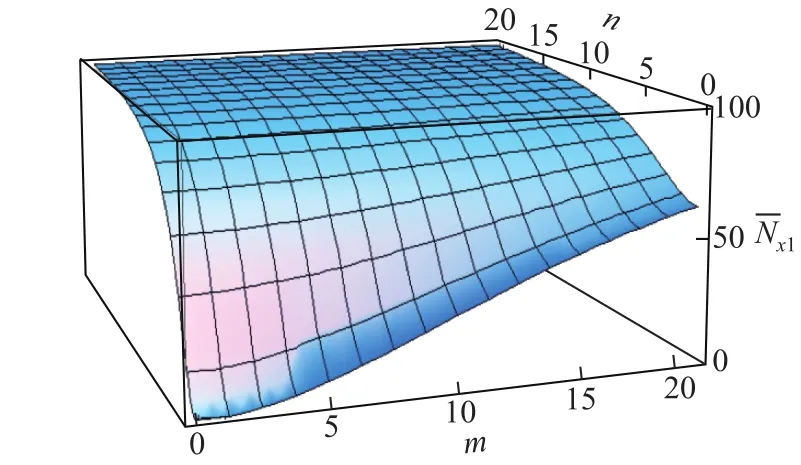
图2 波数m,n对屈曲力的影响Fig.2 E ff ects of wave numbers on buckling loads

由图2可知,波数m,n对屈曲力的影响较大.为了观察非局部理论下,非局部参数对屈曲力的影响,本工作选取了不同的非局部参数(e0a=0,0.5,1.0,2.0)进行计算.当e0a=0时,即为经典连续介质理论下的计算结果.分析计算结果可以看出,当非局部参数逐渐增大,即系统的内部结构对屈曲外载荷的影响更大时,屈曲力逐渐减小,且在波数较大时非局部参数对屈曲力的影响更加显著(见图3,此时ΔT=100K,Γ=1,ξ=0.1,Λ=10,ψ=1,δ=1).因此,当屈曲波数逐渐增大时,系统自身内部的结构对屈曲力的影响效果也会增加,导致非局部理论下的屈曲力比经典弹性理论下的屈曲力更显著地减小.结果表明,非局部理论下该系统内部结构之间的相互作用使得材料的弯曲刚度降低,系统所需屈曲力有所减小,同时在非局部理论下系统更容易发生后屈曲现象.

图3 当波数m,n逐渐增大时,非局部参数对屈曲力的影响Fig.3 E ff ects of scale coefficients on buckling loads

当屈曲波数和非局部参数取定时,本工作分析了厚度比、弹性模量比以及温度变化对屈曲力的影响.当取波数m=n=1,非局部参数e0a=0.5时,屈曲力会随着厚度比和弹性模量比的增大而增大,且厚度比对屈曲力的影响更为明显(见图4和5,此时Γ=1,Λ=10,ψ= 1,δ=1,ΔT1=100,ξ=0.1).

图4 厚度比变化对屈曲力的影响Fig.4 E ff ects of thickness ratios on buckling loads

从图6的结果可以看出,当温度变化ΔT的取值为0～200K时,当温度场的温度降低时,随着温度变化值的逐渐增大,所需的屈曲力也逐渐增大;当温度场的温度升高时,随着温度变化值的逐渐增大,所需的屈曲力逐渐减小(此时Γ=1,ξ=0.1,Λ=10,ψ=1,δ=1,e0a=0.5).

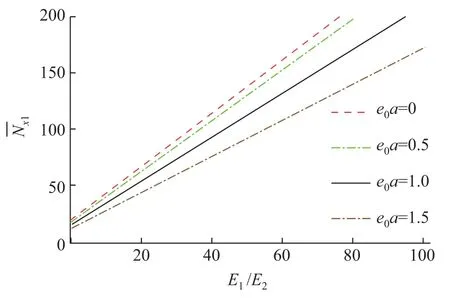
图5 弹性模量比变化对屈曲力的影响Fig.5 E ff ects of elastic modular ratios on buckling loads

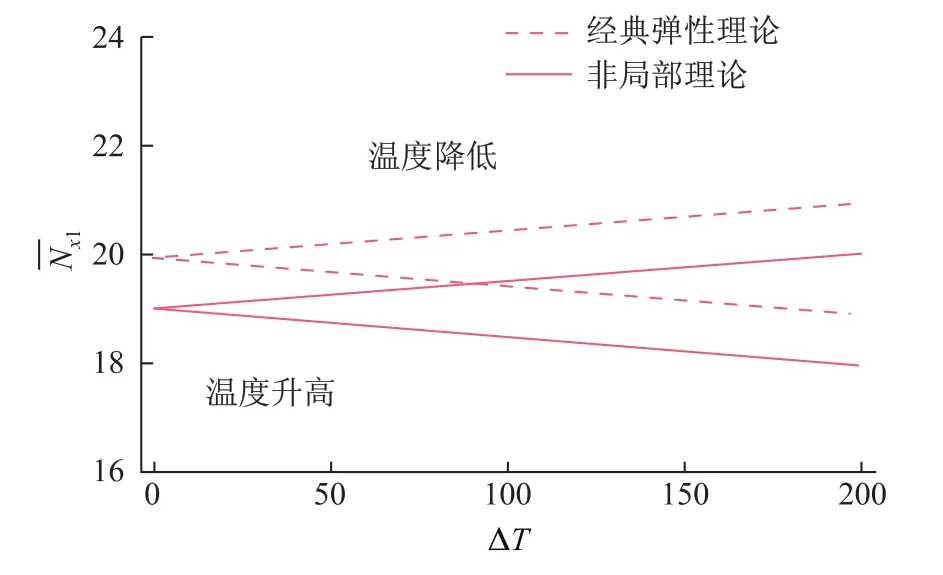
图6 均匀温度场下,温度变化值对屈曲力的影响Fig.6 E ff ects of changes in temperature on buckling loads

3 非均匀温度场下的结果分析

在实际工程背景中,器件所处温度场在通常情况下不是均匀变化的,即当器件在工作过程中受到周围温度场的影响时,可能是边界上的温度变化后沿着器件线性传递下去,也就是说器件所受温度场的变化是非均匀膨胀的.本工作对模型边界受热后,沿着长宽方向线性变化的非均匀温度场进行了分析,研究了温度沿x轴线性变化和沿x,y轴线性变化的两种情况.取ΔT2=xT0(0≤x≤a)和ΔT3=(x+y)T0(0≤x≤a,0≤y≤b).当在模型的一条宽度方向的边界上受到温度变化,产生线性变化的温度场时,有

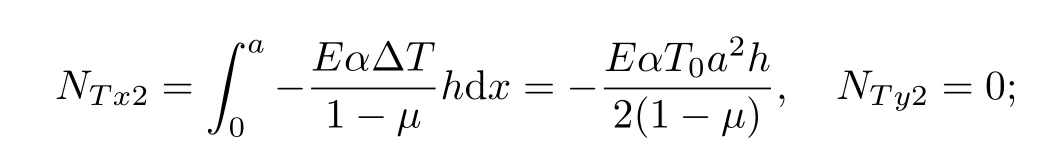
当在模型的一条长和一条宽的边界上受到温度变化,产生长宽方向的线性变化的温度场时,有

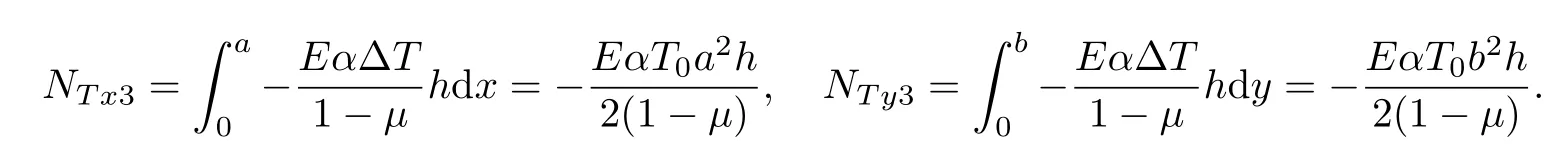
在不同的温度场下,温度变化对屈曲力的影响也有很大差别,而且当沿着模型的长宽线性变化时,模型的尺度对温度影响的结果起到了决定性的作用.由图7可知,当a=b=10时, ΔT3对屈曲力的影响最为显著,其次是ΔT2,影响最小的是均匀温度场的情况(此时Γ=1,ξ= 0.1,Λ=10,ψ=1,δ=1,e0a=1).3种温度场下非局部理论值都有所减小.

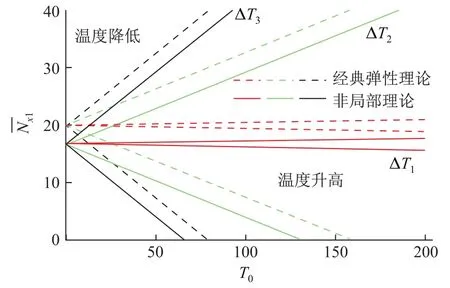
图7 3种温度场下,温度变化对屈曲力的影响关系对比Fig.7 E ff ects of temperature changes on buckling loads

除了直观的温度场差异对屈曲力有所影响外,不同的模型的尺度参数也是不同温度场影响屈曲力的决定性因素.如图8所示,在均匀温度场下,温度变化对屈曲力的影响不因模型尺度的变化而改变(此时T0=100,ξ=0.1,Λ=10,ψ=1,δ=1,e0a=1.0,b=5);但在非均匀温度场下,当模型的长宽比逐渐增大时,沿轴向线性变化的温度场对屈曲力的影响也会有所增加.当宽度为固定值时,随着长宽比的增大,即长度a逐渐增大,在x轴向上的温度应变也逐渐增加,从而使得温度应力逐渐变大,导致非均匀温度场对屈曲力的影响进一步显著.因此在不同的温度场下,温度场的作用结果和系统的尺度有很大的关系,在非均匀温度场下分析温度变化对屈曲力的影响时应该认真考虑模型的尺度大小.

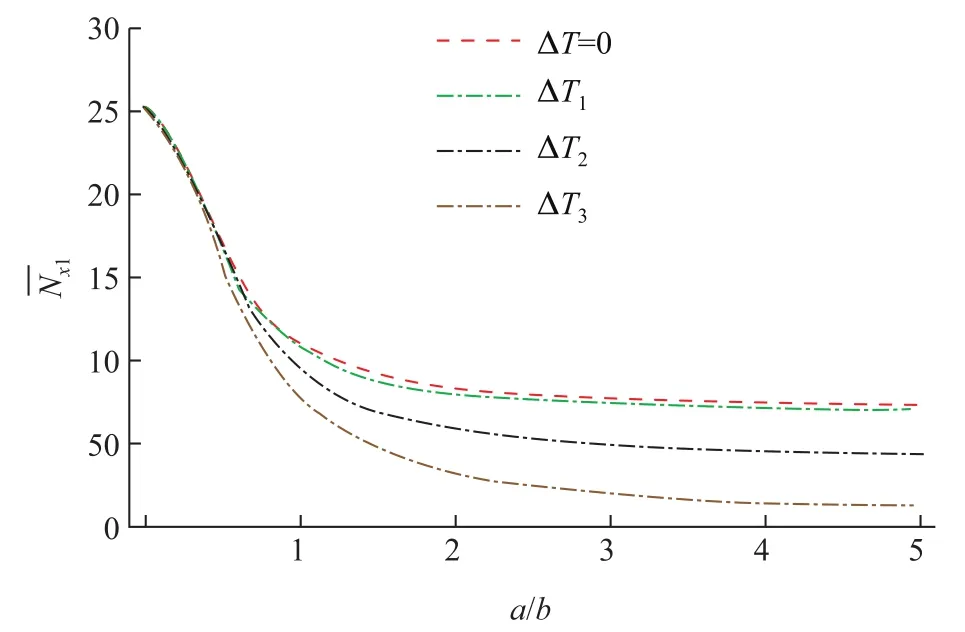
图8 随着长宽比的变化,3种温度变化值对屈曲力的影响关系对比Fig.8 E ff ects of length-width ratios on buckling loads in di ff erent temperature changes

4 结束语

本工作基于非局部理论,对双层完好粘接板在受双轴压缩和温度耦合作用下的屈曲稳定性进行了研究分析,主要讨论了如下两点内容:①非局部理论下屈曲力的变化;非局部参数的影响结果与波数的关系;在均匀温度场下,温度变化、弹性模量比和厚度比对屈曲力的影响;②非均匀温度场下,两种沿轴向线性变化温度场对屈曲力的影响,以及3种温度场作用结果的对比.通过计算分析得到,厚度比和弹性模量比的增大都会导致屈曲力的增大,并且厚度比的变化对屈曲力的影响更大.在非局部理论下,由于系统内部自身结构之间的相互作用,使得系统的屈曲力有所减小,尤其是在小尺度及较大屈曲波数下,非局部参数对屈曲力的影响尤为显著.这一结果表明,系统内部结构之间相互作用会导致系统的弯曲刚度有所减小,导致屈曲力的降低,且在系统尺度较小和屈曲波数增大使得内部相互作用域收缩时,外部尺度更接近内部相互作用结构的尺度,导致非局部参数对屈曲力的影响更大.在双轴压缩和温度场耦合作用下,当温度降低(升高)时会导致屈曲力增大(减小).在均匀温度场下,温度变化对屈曲力的影响不受系统大小的影响,但在非均匀温度场下,系统的尺寸也与温度场对屈曲力的影响结果有关.

[1]CHEN X,HUTCHINSON J W.Herringbone buckling patterns of compressed thin fi lms on compliant substrates[J].Journal of Applied Mechanics,2004,71(5):597-603.

[2]HUANG R.Kinetic wrinkling of an elastic fi lm on a viscoelastic substrate[J].Journal of the Mechanics and Physics of Solids,2005,53(1):63-89.

[3]HUANG R,SUO Z.Instability of a compressed elastic fi lm on a viscous layer[J].International Journal of Solids and Structures,2002,39(7):1791-1802.

[4]HUANG R,SUO Z.Wrinkling of a compressed elastic fi lm on a viscous layer[J].Journal of Applied Physics,2002,91(3):1135-1142.

[5]LI B,HUANG S Q,FENG X Q.Buckling and postbuckling of a compressed thin fi lm bonded on a soft elastic layer:a three-dimensional analysis[J].Arch Appl Mech,2010,80(2):175-188.

[6]ERINGEN A C.Nonlocal polar elastic continua[J].International Journal of Engineering Science, 1972,10(1):1-16.

[7]ERINGEN A C.On di ff erential-equations of nonlocal elasticity and solutions of screw dislocation and surface-waves[J].Journal of Applied Physics,1983,54(9):4703-4710.

[8]ERINGEN A C.Nonlocal contimuum fi eld theories[M].New York:Springer,2001.

[9]SHEN H S.Nonlocal plate model for nonlinear analysis of thin fi lms on elastic foundations in thermal environments[J].Composite Structures,2011,93(3):1143-1152.

[10]PIjAUdIER S M G,BAZANT Z P.Nonlocal damage theory[J].Journal of Engineering Mechanics, 1987,113(10):1512-1533.

[11]BAZANT Z P.Nonlocal damage theory based on micro-mechanics of crack interactions[J].Journal of Engineering Mechanics,1994,120(1):593-617.

[12]PRAdHAN S C.Buckling of single layer graphene sheet based on nonlocal elasticity and higher order shear deformation theory[J].Phys Lett A,2009,373(45):4182-4188.

[13]PRAdHAN S C,MURMU T.Small scale e ff ect on the buckling of single-layered graphene sheets under bi-axial compression via nonlocal continuum mechanics[J].Computational Material Science,2009,47(1):268-274.

[14]PRAdHAN S C,MURMU T.Small scale e ff ect on the buckling analysis of single-layered graphene sheet embedded in an elastic medium based on nonlocal plate theory[J].Physica E,2010,42(5): 1293-1301.

[15]WANG Q,LIEW K M.Application of nonlocal continuum mechanics to static analysis of microand nano-structures[J].Physics Letters A,2007,363(3):236-242.

[16]SAMAEI A T,ABBASION S,MRISAYAR M M.Buckling analysis of a single-layer graphene sheet embedded in an elastic medium based on nonlocal Mindlin plate theory[J].Mechanics Research Communications,2011,38(7):481-485.

[17]AGHABABAEI R,REddY J N.Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates[J].Journal of Sound and Vibration,2009,326(1/2): 277-289.

[18]ARASH B,WANG Q.A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes[J].Computational Materials Science,2012,188(51):57-82.

[19]NARENdAR S.Buckling analysis of micro-/nano-scale plates based on two-variable re fi ned plate theory incorporating nonlocal scale e ff ects[J].Composite Structures,2013,93(12):3093-3103.

[20]HAO M J,GUO X M,WANG Q.Small-scale e ff ect on torsional buckling of multi-walled carbon nanotubes[J].European Journal of Mechanics A/Solids,2010,29(1):45-55.

[21]WANG Y Z,CUI H T,LI F M,et al.Thermal buckling of a nanoplate with small-scale e ff ects[J].Acta Mech,2013,224(6):1299-1307.

[22]KUMAR T J P,NARENdAR S,GOpALAKRISHNAN S.Thermal vibration analysis of monolayer graphene embedded in elastic medium based on nonlocal continuum mechanics[J].Composite Structures,2013,100(1):332-342.

本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn

Scale e ff ect on buckling of bonding materials under biaxial compression with temperature changes

LIU Liang,PENG Xiang-wu,WANG Qing-zhan,GUO Xing-ming
(Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University, Shanghai 200072,China)

The scale e ff ect on buckling of bonding materials under biaxial compression coupled with temperature changes is studied.A developed nonlocal plate theory is applied to study the buckling behavior of the nonlocal multiple-plate model.The Navier’s approach is used to obtain exact solutions for buckling loads under simply supported boundary conditions.The e ff ects of the scale coefficient,wave number,thickness ratio,elastic modular ratio and temperature changes on the buckling loads are investigated.It is shown that the critical buckling force may be overestimated with the classical continuum theory.The nonlocal e ff ect is proved to be more prominent for higher buckling modes.In addition, three kinds of temperature changes are taken into account.The in fl uence of temperature changes on the buckling loads and the relationship with the system size are analyzed.

nonlocal elastic theory;bonding material;buckling;biaxial compression; temperature change

O 34

A

1007-2861(2015)04-0422-10

10.3969/j.issn.1007-2861.2014.02.007

2014-03-04

国家自然科学基金资助项目(10972128,11472163)

郭兴明(1964—),男,教授,博士生导师,研究方向为微纳米力学、材料的多尺度力学建模、连续介质力学. E-mail:xmguo@shu.edu.cn