窄通道中近可燃极限预混火焰的结构和稳定性

陈晓通,卢占斌

(上海大学上海市应用数学和力学研究所,上海 200072)

窄通道中近可燃极限预混火焰的结构和稳定性

陈晓通,卢占斌

(上海大学上海市应用数学和力学研究所,上海 200072)

通过数值方法研究了窄通道中近可燃极限预混火焰的结构和稳定性.窄通道由上、下两个圆形平行平板构成,燃气和氧气组成的混合气体充满窄通道内部,点燃后形成的预混火焰在一定条件下有可能稳定在窄通道内.采用基于Arrhenius单步反应的反应-扩散火焰模型,考察了平板间距、平板材料和平板半径对火焰的影响.结果表明,一定的平板间距下主要有两个火焰的稳态解:一个对应较大的火焰半径,另一个对应较小的火焰半径.通过线性稳定性分析发现,窄通道中存在一维稳定的火焰,但不存在二维稳定的火焰.对一维稳定但二维不稳定的火焰的失稳进行数值模拟可以发现,失稳主要表现为火焰整体向边界漂移,或者一个火焰分裂成两个新的火焰后分别沿相反方向向边界漂移.

窄通道;预混火焰;可燃极限;稳定性

利用氢气、碳氢化合物等作为燃料的微小型燃烧装置具有能量密度高的特点,在微机电系统中有着广泛的应用前景[1].这种潜在的需求直接带动了微尺度燃烧的研究热潮.在过去十几年中,人们研究了各种微尺度(或介观尺度)受限空间内预混火焰、扩散火焰以及边界火焰的燃烧特性,发现了许多微尺度燃烧的独特现象[2-3].

本工作研究了窄通道内接近可燃极限的预混火焰的燃烧特性.当远离可燃极限时,燃气和氧气组成的混合气体在刚点燃时形成的球形预混火焰波一般会以某一速度向外传播,以此来完成整个燃烧过程.相反,当燃气浓度趋近于可燃极限时,随着预混火焰传播速度的减小,火焰向外界的辐射热损失会逐渐占据主导地位.因此可以预见,当趋近可燃极限时,向外传播的球形预混火焰可能会在辐射热损失的作用下在某一半径处停止,从而形成一个静态的火球.混合气体的热扩散率与反应的质量扩散率之比即为Lewis数.当接近可燃极限的混合气体的Lewis数小于1时,如果没有气体的辐射热损失,反应的质量扩散作用就会占主导地位,以致形成半径一直增大的球面形火焰.当有气体辐射热损失时,火球的热损失可随火球半径的增大而加强,与质量扩散作用相平衡,使火球静止.Zeldovich等[4]首次在理论上预言了火球的存在,但稳定性分析表明绝热火球是不稳定的.直到1990年,Ronney[5]才在落塔实验中首次观察到了稳定存在的火球.理论分析表明,如果考虑到火球向外界的热损失,火球可以存在两个稳态解分支,其中一个对应半径较大的火球,另一个对应半径较小的火球[6-8].通常,前者有一部分是三维不稳定的,有一部分是稳定的,而后者则是一维不稳定的.Ronney等[9]于1997年在航天飞机上进行了一系列实验.这些实验发现了火球的漂移现象,加深了人们对火球以及燃烧动力学的认识.Lu等[10]指出火球之间存在一个临界距离,当大于临界距离时,火球相互排斥并沿相反方向漂移,反之则会相互吸引最终融合成一个新的火球.

自Ronney实验以后,火球作为一种微重力条件下特有的有趣的燃烧现象,一直未能找到其潜在的应用价值.本研究考虑了窄通道内近可燃极限预混火焰燃烧,试图将火球引入到微尺度燃烧的框架内.概括地讲,本研究的基本思路是用两个平行平板从两侧挤压一个处于三维无限空间中的火球,来考察这个被压扁了的火球的响应,其中主要的控制参数包括两个平行平板之间的距离、平板和预混气体的热物性参数等.需要指出的是,Shah等[11]曾分析了处于多孔介质中的火球,与本研究有一定的相关性,但他们只考虑了火球与多孔介质之间的传热,而没有考虑多孔介质本身的热传导作用.相反,在本研究中,平行平板内部的热传导将对火焰的结构和稳定性起决定性作用.

1 物理模型和数学模型

1.1 建立模型

考虑轻型气体燃料和氧气的混合气体,混合气体近可燃极限,处于两个圆形平行平板间的窄通道中.燃烧反应采用如下的Arrhenius单步反应模型:

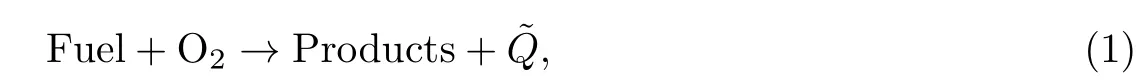
图1为反应装置的示意图.本研究采用了反应-扩散模型,假定气体密度是常数,气体和平板的热物性参数都是均匀恒定的.有量纲形式的控制方程为

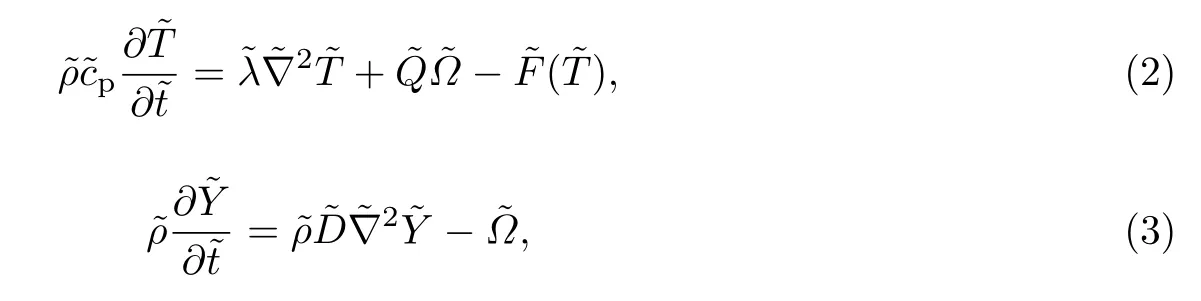
图1 具有两个平行平板的燃烧器Fig.1 A combustor with two parallel plates

反应率采用经典的Arrhenius形式,即

1.2 一维线性近似

如果两平板的间距较小,那么就可以对气体的能量和质量守恒方程进行一维线性近似[12].以上平板为例,在二维结构下,气体与壁面的热流量为

进行一维线性近似后,气体在壁面处的温度梯度可近似为

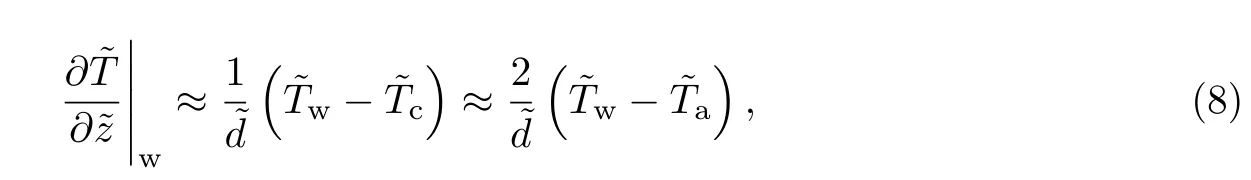
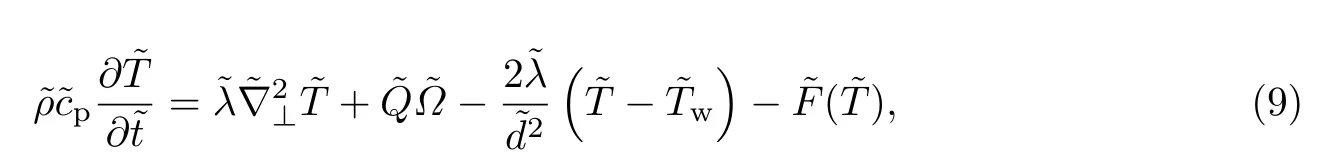
1.3 无量纲化

2 分析与讨论

2.1 一维稳态解

计算时选取的参数如表1和2所示.

表1 气体的物理参数Table 1 Physical parameters of gas

表2 平板的物理参数Table 2 Physical parameters of the plate

方程(24)～(26)的空间导数采用四阶中心差分离散化.以d为参数,运用连续性方法[13],可以得到柱形火焰半径R关于d的响应曲线,结果如图2和3所示.

图2反映了平板导热性能对响应曲线的影响.导热性能最好的平板对应的响应曲线d的取值范围最大,反之亦然.可以看出,对于相同尺寸的玻璃、钢质和铝质平板,铝质平板的导热性能最好,玻璃平板的导热性能最差,对于同样的d,在曲线的下支平板导热性能越好,柱形火焰的半径就越小,上支的情况与此相反.

图3反映了同种材料下平板半径变化对响应曲线的影响.可见,平板半径越大,响应曲线d的取值范围就越大.对于同样的d,在曲线的下支平板半径越大,柱形火焰的半径越小,上支的情况与此相反.

图4(a)表明,除了右边界处平板温度和气体温度都等于θf外,同一半径处的平板温度都低于气体温度;因为平板的导热较大,所以与气体相比,平板的温度在径向变化较小;气体的最高温度位于半径r=9处,平板的最高温度则位于r=0处.图4(b)表明,反应率的最大值在半径r=10处,即柱形火焰的半径R=10.

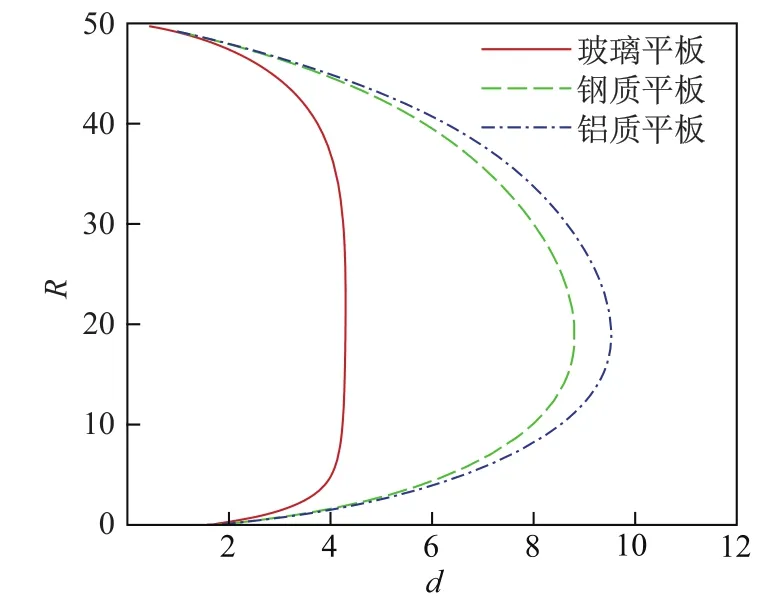
图2 rb=50的圆形玻璃平板、钢质平板及铝质平板对应的柱形火焰的响应曲线Fig.2 Responses of the fl ame cylinder corresponding to circular plates of glass,steel and aluminum with rb=50

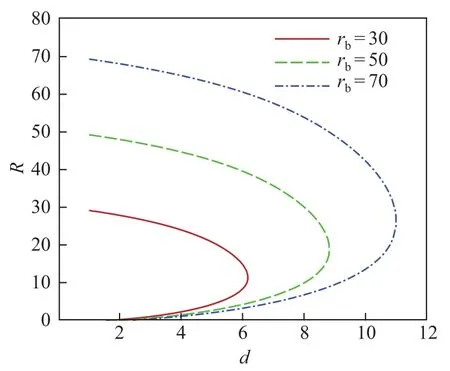
图3 rb=30,50,70的圆形钢质平板对应的柱形火焰的响应曲线Fig.3 Responses of the fl ame cylinder corresponding to circular plates of steel with rb=30, 50,70

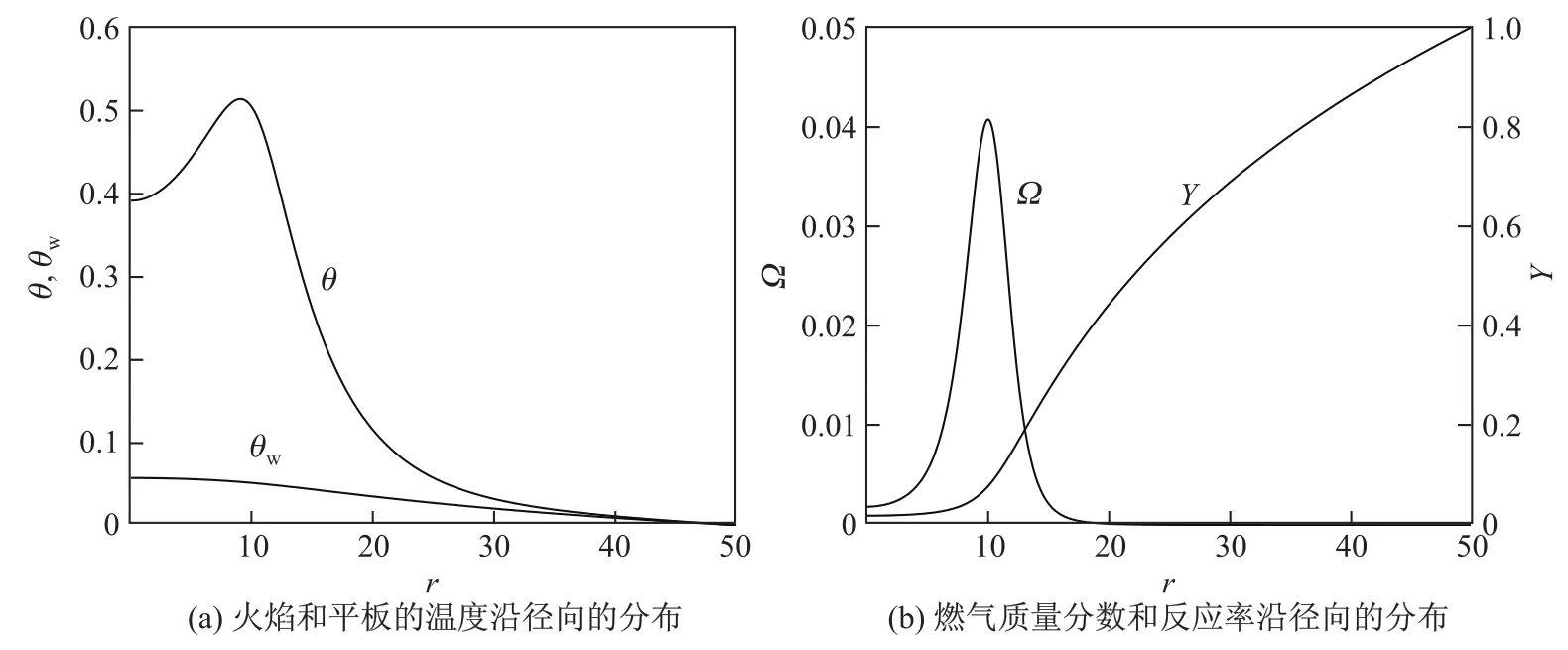
图4 当圆形钢质平板rb=50且d=8时,柱形火焰的温度、燃气质量分数、反应率和平板的温度沿径向的分布Fig.4 Radial pro fi les of temperature,fuel mass fraction and reaction rate of the fl ame cylinder and temperature of the circular steel,as the plate rb=50 and d=8

2.2 线性稳定性分析

本研究用正则模的方法研究了柱形火焰的线性稳定性,稳态解用上标“*”标明.引入小扰动后得到如下的扰动函数:

图5中的实线部分为一维稳定区间,但它是二维不稳定的,此时d∈[2.1,6.6],虚线部分则是一维和二维都不稳定的.可见,整条响应曲线都是二维不稳定的.一维稳定区间分两个部分:在d∈[2.1,5.2]部分进行稳定性分析时发现,只有当波数m=1时特征值的实部大于0;在d∈[5.3,6.6]部分发现,只有当波数m=1和2时特征值的实部大于0,且m=2时特征值的实部较大.改变平板材料和半径,运用同样的方法进行分析可以得到,rb=30,50,70三种情况下的玻璃、钢质和铝质平板对应的响应曲线总是存在一维稳定的区间,但整条响应曲线都是二维不稳定的.

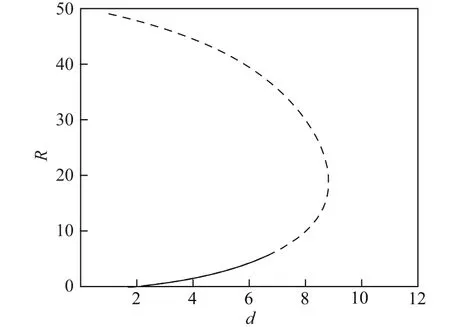
图5 当圆形钢质平板rb=50时,柱形火焰响应曲线的一维稳定区间(实线部分)Fig.5 1D stable spectrum(solid line)of the response of the fl ame cylinder,as the circular steel plate rb=50

选取边长为100的正方形区域,以区域的几何中心为坐标原点,在初始没有火焰时,区域内部和边界均为θ=θw=θf,Y=Yf.将图5所示的d=5.2,R=3和d=6.4,R=5.2的柱形火焰分别放在上述区域中,边界条件固定为θ=θw=θf,Y=Yf,施加随机小扰动后火焰随时间的变化分别如图6和7所示(仅为局部显示),其中图6中的火焰向一侧的边界漂移,图7中火焰一分为二后形成的两个火焰沿相反方向向边界漂移.图6和7反映了二维不稳定的柱形火焰失稳的两种典型现象:若线性稳定性分析的结果为波数m=1时特征值的实部为正且最大,则失稳与图6的情形近似;若线性稳定性分析的结果为波数m=2时特征值的实部为正且最大,则失稳与图7的情形近似.从图中还可以看出,火焰越靠近边界处漂移速度越快.火焰的存在需要充足的燃气供应和较高的温度这两个因素.进一步计算发现,虽然边界处温度较低,但是火焰最终仍会漂移到很靠近边界的位置.这表明燃气的质量扩散作用强于火焰的热量扩散作用.

图6 在时间t=0,800,1 040,1 104时,柱形火焰的反应率等值线(等值线为0.05,0.15,0.25,0.35)Fig.6 Reaction rate contours of a fl ame cylinder at times t=0,800,1 040,1 104(contour levels are 0.05,0.15,0.25,0.35)

图7 在时间t=0,35,90,125时,柱形火焰的反应率等值线(等值线为0.04,0.08,0.12,0.16,0.20, 0.24,0.28)Fig.7 Reaction rate contours of a fl ame cylinder at times t=0,35,90,125(contour levelsare 0.04,0.08,0.12,0.16,0.20,0.24,0.28)

3 结束语

本研究忽略了气体的辐射热损失和平板向外界环境的散热,对控制方程进行了一维线性近似,采用数值模拟的方法研究了由两个圆形平行平板构成的四周开放的窄通道中火焰的结构和稳定性.一维简化后火焰是柱形的.对于不同材料以及不同半径的平板,板间距的一半d与火焰一维解的关系表明,稳态解主要有两个分支:一个分支对应较大的火焰半径,另一个对应较小的火焰半径,平板导热性能提高或平板半径增大都会使这两个解分支的临界点右移并且使d的取值范围变大.对于选定的几种材料和半径的平板,线性稳定性分析表明,其间的火焰是不稳定的.火焰的失稳主要有两种情形:若稳定性分析结果为波数m=1时特征值的实部为正且最大,则火焰整体向一侧的边界漂移;若稳定性分析结果为波数m=2时特征值的实部为正且最大,则火焰一分为二后形成两个火焰沿相反方向向边界漂移.

柱形火焰受到扰动后温度可能在周向分布不均匀,进而失去稳定性,气体的辐射热损失和平板向外界环境的散热有阻碍这种变化的作用.但是进一步计算发现,它们都不足以使火焰稳定下来.与提高平板导热性能的作用相似,增加这两种热损失会使柱形火焰半径R关于d的响应曲线上支升高,下支降低,两个分支的临界点右移,d的取值范围变大.需要指出的是,平板以辐射和自然对流方式向室温环境散热时对火焰的影响远小于平板自身的导热作用.气体的辐射热损失和平板向外界环境的散热对平板间柱形火焰的结构和稳定性没有决定性影响,因此本研究不考虑这两种因素.平板间实际的火焰不是柱形的,应是接近扁球形的.一维线性近似可以定性反映平板作用下火焰的结构和稳定性,但是与实际情况相比高估了气体的散热.实际情况下火焰最大半径R关于d的响应曲线也应有两个解分支,与一维线性近似的结果相比,上支较低、下支较高,两个分支的临界点对应的d值较小,且d的取值范围也较小.

考虑到柱形火焰失稳的机理,通过改造燃烧器模型可以得到稳定的火焰.燃气从低温区向火焰扩散并有加强燃烧的作用,温度的扩散则沿相反方向并有减弱燃烧的作用.燃气的质量扩散作用强于火焰的温度扩散作用,从而使火焰漂移到非常靠近边界的位置.因此,可使平行平板构成的窄通道的边界温度维持在θf,边界只有一部分开放而其他部分封闭,燃气质量分数为Yf的混合气体仅通过开放部分进入平板间.这样燃气从边界向火焰的扩散作用就减弱了,可能和火焰的温度扩散作用相平衡从而形成稳定的火焰.

[1]FERNANdEZ-PELLO A C.Micropower generation using combustion:issues and approaches[J]. Proceedings of the Combustion Institute,2002,29(1):883-899.

[2]MARUTA K.Micro and mesoscale combustion[J].Proceedings of the Combustion Institute,2011, 33(1):125-150.

[3]JU Y,MARUTA K.Microscale combustion: technology development and fundamental research[J].Progress in Energy and Combustion Science,2011,37(6):669-715.

[4]ZELdOVICH Y B,BARENBLATT G I,LIBROVICH V B,et al.The mathematical theory of combustion and explosions[M].New York:Consultants Bureau,1985:327.

[5]RONNEY P D.Near-limit fl ame structures at low Lewis number[J].Combustion and Flame, 1990,82(1):1-14.

[6]BUCKMASTER J,JOULIN G,RONNEY P.The structure and stability of nonadiabatic fl ame balls[J].Combustion and Flame,1990,79(3/4):381-392.

[7]BUCKMASTER J D,JOULIN G,RONNEY P D.The structure and stability of nonadiabatic fl ame balls:Ⅱ.E ff ects of far- fi eld losses[J].Combustion and Flame,1991,84(3/4):411-422.

[8]BUCKMASTER J,SMOOKE M,GIOVANGIGLI V.Analytical and numerical modeling of fl ame-balls in hydrogen-air mixtures[J].Combustion and Flame,1993,94(1/2):113-124.

[9]RONNEY P D,WU M S,PEARLMAN H G,et al.Structure of fl ame balls at low Lewis-number (SOFBALL):preliminary results from the STS-83 space fl ight experiments[J].AIAA J,1998, 36:1361-1368.

[10]LU Z,BUCKMASTER J.Interactions of fl ame balls[J].Combustion Theory and Modelling,2008, 12(4):699-715.

[11]SHAH A A,THATCHER R W,DOLd J W.Stability of a spherical fl ame ball in a porous medium[J].Combustion Theory and Modelling,2000,4(4):511-534.

[12]SpALdING D.A theory of in fl ammability limits and fl ame-quenching[J].Proceedings of the Royal Society of London:Series A—Mathematical and Physical Sciences,1957,240(1220):83-100.

[13]RHEINBOLdT W C,BURKARdT J V.A locally parameterized continuation process[J].ACM Transactions on Mathematical Software,1983,9(2):215-235.

本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn

Structure and dynamics of near-limit premixed fl ames in narrow channels

CHEN Xiao-tong,LU Zhan-bin
(Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University, Shanghai 200072,China)

Structure and dynamics of near-limit premixed fl ames in narrow channels are numerically studied.The channel consists of two circular parallel plates,one of which is upward and another is downward.It is possible that the premixed fl ame is stable when the mixture of fuel gas and oxygen in the channel is ignited.A reaction-di ff usion model is used based on the Arrhenius-type chemistry,and attention is focused on the in fl uence of distance between two plates as well as the plate’s material and radius.There are mainly two steady solutions for a given distance between the plates,a small fl ame and a large fl ame. Linear stability analysis shows that 1D stable fl ames may exist in the narrow channel,but 2D stable fl ames do not exist.The dynamical evolution processes of 1D stable,but 2D unstable fl ames are studied by direct numerical simulations.It is shown that the fl ame drifts to the boundary as a whole or an old one splits into two new fl ames that drift to the boundary along the opposite direction.

narrow channel;premixed fl ame; fl ammability limit;stability

TK 16

A

1007-2861(2015)04-0444-10

10.3969/j.issn.1007-2861.2014.01.014

2014-01-08

上海市科委启明星计划资助项目(09QA1402300)

卢占斌(1975—),男,副研究员,博士,研究方向为燃烧与火焰理论.E-mail:zblu@sta ff.shu.edu.cn