扑翼不同的运动方式对其获能影响的数值模拟

韩 伟, 孙晓晶

(1.上海大学上海市应用数学和力学研究所,上海 200072; 2.上海理工大学能源与动力工程学院,上海 200093)

扑翼不同的运动方式对其获能影响的数值模拟

韩 伟1, 孙晓晶2

(1.上海大学上海市应用数学和力学研究所,上海 200072; 2.上海理工大学能源与动力工程学院,上海 200093)

翼型在风或水流中扑动既可以作为一种推进方式也可以在改变运动参数后从中获取能量.通过控制波形参数得到扑翼的升沉和俯仰运动波形,并利用非定常数值模拟来研究St数、俯仰幅值和升沉俯仰运动的波形对其获能效率的影响.同时,还研究了不同的扑动俯仰轴位置对扑翼获能效率的影响.研究结果表明,在获能参数域内俯仰运动的波形和俯仰轴位置会对扑翼获能产生较大的影响,而升沉运动的波形对扑翼获能的影响有限,且当St=1.332, θ0=76.3◦,βt和βr分别为1.13(此时的俯仰波形为接近正弦波)和0.67时,翼型扑动获能的效率最高,为41%.

风能(水流能)利用;扑翼;运动规律;非定常数值模拟

风能和水流能是两种高效的清洁可再生能源.除了传统的水平轴和垂直轴风力机,受到鸟类扑翼可高效飞行的启发,出现了一种新型的通过翼型扑动来获能的风力(水力)机.这种新型的风力(水力)机因其可以轻松地在传统旋转透平机无法施展的水渠和城市建筑群中高效获能,而成为了风能水流能利用的新方向.

1981年,McKinney等[1]首次对单个翼型的扑动获能进行了实验研究.该装置的获能效率与当时的风力机相当.1997年,Jones等[2]研究发现,扑动运动在一定频率下会增大俯仰运动的幅值,产生阻力并且从流体中获得能量.Jones等[3]对于翼型扑动获能的研究发现,前缘涡的产生以及涡与翼型的相互作用对获能效率有很大的影响.他们以及后来的Kinsey等[4]都认为,当俯仰幅值为73◦时,获能效率最佳.2010年,Xiao等[5]利用波形参数β对俯仰运动的时间波形进行控制,实现了俯仰波形从正弦波形到矩形波形的变化,升沉运动仍保持正弦波形.数值模拟结果表明,与正弦俯仰运动相比,非正弦俯仰运动的输出的功率系数增长了63%,能量利用率增长了50%.2011年,Ashraf等[6]对非正弦俯仰运动进行了数值模拟,得到的功率和效率比正余弦俯仰运动的情况分别增加了17%和15%.

扑翼运动可以看作是翼型在平面内的升沉平动和绕平动平面内一点的俯仰运动的合运动(见图1,其中h0为升沉运动幅值,θ0为俯仰运动幅值,c为翼型弦长,d为翼型的扫略距离).升沉运动所获得的功率为升沉力与升沉速度的乘积,即Py(t)=Y(t)Vy(t).俯仰运动所获得的功率为俯仰力矩与俯仰角速度的乘积,即Pθ(t)=M(t)Ω(t).无量纲时均总功率系数为升沉力时均功率系数与俯仰时均功率系数之和,即

当时均总功率为正值时,流体对扑翼做正功,扑动从流体中获能;反之,流体对扑翼做负功,扑动需要额外提供能量.获能效率为

式中,升沉力系数为

俯仰力矩系数为

图1 扑翼运动(φ=90◦)Fig.1 Flapping movement(φ=90◦)

1 运动方程

本研究将Xiao等[5]的俯仰运动波形方程扩展到了三角波形,同时通过参数改变升沉运动的波形,来研究波形组合对扑翼获能效率的影响.根据扑翼获能的必要不充分条件[4],大体上可将波形参数的选取范围控制在获能区域内.参数βt控制升沉波形,当βt从1增大到+∞时,升沉运动方程的波形从时间余弦波变化到时间三角波.参数βr控制俯仰运动的波形,随着βr的增大,俯仰运动的波形从时间矩形波变化为时间正弦波(βr=1),最后变为时间三角波.升沉和俯仰波形变化分别如图2和3所示.

图2 不同βt对应的升沉运动Fig.2 Translations of the pitching axis for di ff erernt βt

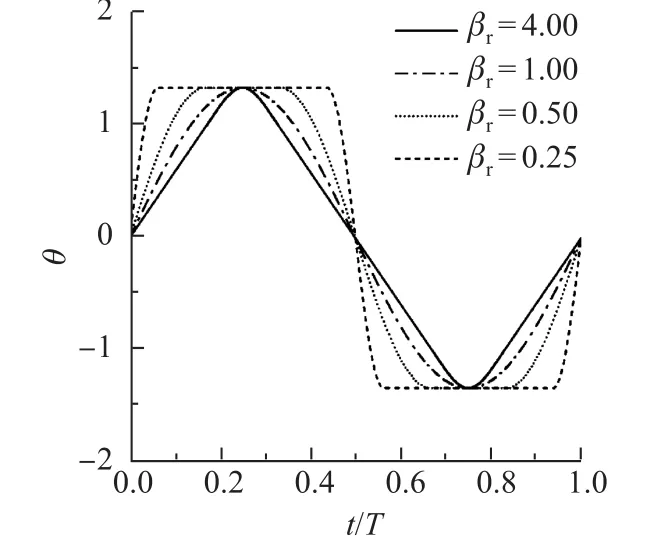
图3 不同βr对应的俯仰运动Fig.3 Rotations around the pitching axis for di ff erernt βr

升沉运动方程为

2 获能的必要条件

由于升沉运动会产生诱导攻角αi,因此扑翼的实际来流攻角为

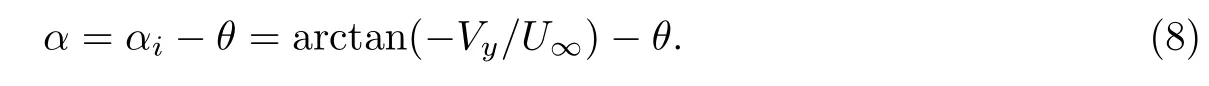
由空气动力学原理可知,对称翼型的攻角为正时升力为正,攻角为负时升力为负.一般认为,翼型扑动实际来流攻角的最大值对气动力的峰值和动态失速的产生有着主要的影响, 1/4周期的来流攻角的绝对值为实际来流攻角的幅值,即

根据准定常方法可以给出扑翼获能的必要不充分条件:αT/4＜0[4].图4给出了获能扑动的扑翼相对于远方来流的运动示意图,其中升力L和阻力D的合力为R.在T/4时刻将R分解为水平和竖直两个分量X和Y,可以看出分量X与扑翼的升沉速度同向,分量Y(升沉力)对扑翼做功.

根据运动方程(5)～(7)可得

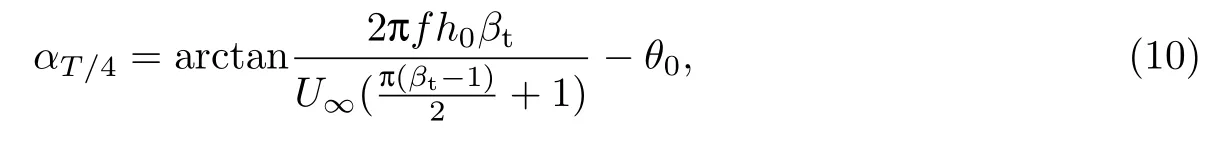
再由扑翼获能的必要不充分条件可得

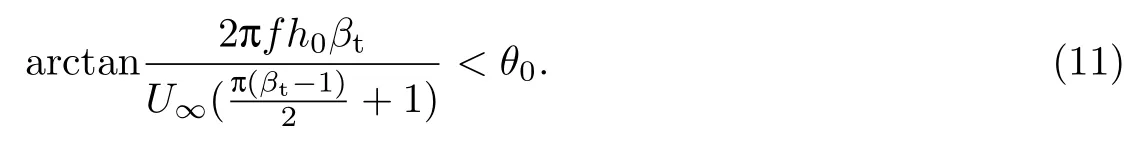
这里把条件加强,令

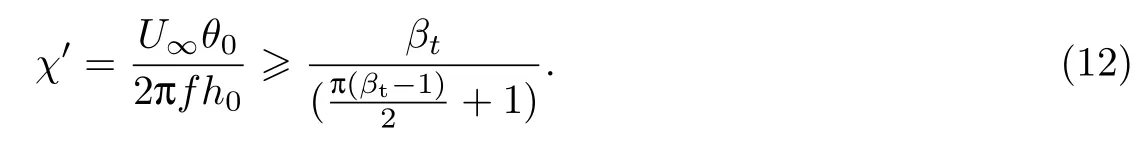
由于给定的扑翼运动得到的χ′是一定的,因此所选的参数βt必须满足上述条件,βr则可以任意选取.

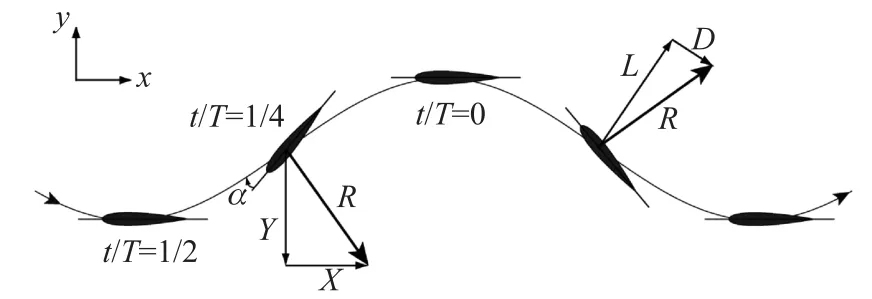
图4 扑翼获能的示意图Fig.4 Schematic diagram of fl apping for power extraction

3 数值模拟

本研究利用本课题组开发的UCFD软件对雷诺数为10 000的NACA0015翼型进行了数值模拟.该软件采用有限体积方法,以焓、速度与压力为原始变量,构建了相应的流体力学预处理方法;用以焓与压力为自变量的任意工质状态方程或热力性质表格来封闭流体力学方程组；用Roe格式离散对流项,通过状态插值法实现格式的高精度.该软件采用多块网格、多重网格、拼接网格、重叠网格、嵌套网格、变形网格以及并行等技术,可以进行任意工质、各种复杂内流与外流的定常、非定常及流固耦合流场的模拟[7-9].

计算网格为O形结构网格,网格总数为38 801.计算域的平均半径约为30倍弦长,流场外边界为速度进出口(马赫数为0.043),整个网格随翼型运动(见图5和6).由于St=2πf∗h0/c,其中无量纲频率f∗=fc/U∞为固定值0.14,因此可通过改变h0/c来改变St.一个运动周期的时间步数为2 000[4].

Kinsey等[10]指出,Spalart-Allmaras(S-A)湍流模型比较适合扑动获能单方程,因此本研究的数值模拟全部采用该湍流模型.

图5 网格Fig.5 Grid

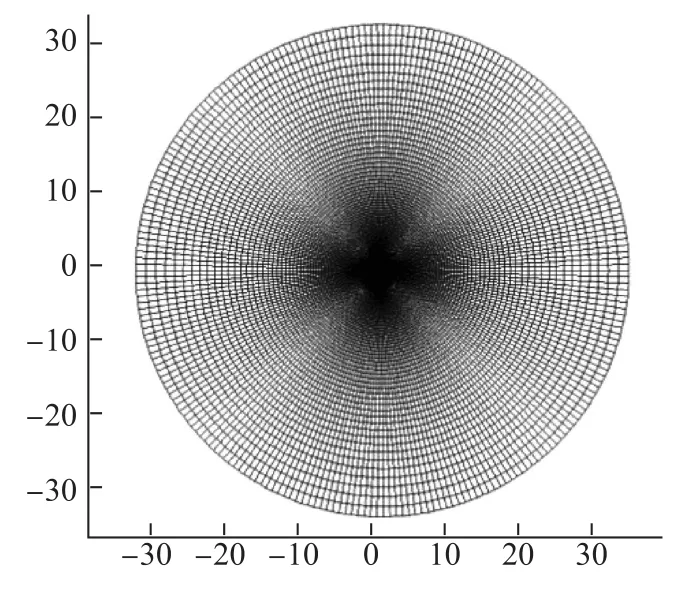
图6 计算流场区域Fig.6 Computation fl owing fi eld

2008年,Simpson等[11]公布了水槽拖曳实验结果.对比其中展弦比为7.9,St=0.6,1/4周期实际来流攻角为-34.4◦的工况,本研究给出了二维数值模拟的网格数和时间步长的验证结果.

由于数值模拟使用的工质为理想气体,为了保证计算结果与实验结果的可比性,根据相似准则,应该保证几何相似、运动相似和动力相似.对于几何相似和运动相似,计算中使用与实验相同的翼型(NACA0012)和无量纲运动规律.对于动力相似,由于水可以看作不可压缩流体,数值模拟的雷诺数取0.01(≪0.3),并在此基础上保证了数值模拟的雷诺数和St数分别为13 800和0.6,以保证了与实验的动力相似.最后,得到的升沉运动幅值为1.23倍翼型弦长,俯仰幅值为85.82◦,无量纲频率为0.16.

本研究给出了精度分别为2×129×65,2×257×129,2×513×257的三套网格,网格数分别为8 192,32 768,131 072.在网格数为131 072的网格上使用了三种时间步长,分别为T/500, T/2 000,T/4 000.根据升沉力系数CY、阻力系数CX和俯仰力矩系数CM在一个周期内的变化情况,可以发现不同大小的时间和空间离散对结果的影响很小(见图7(a)～(c),其中Vy为升沉速度,ω为俯仰角速度).

从时均功率上看,2×257×129网格在时间步长为T/2 000时的升沉力时均功率与2× 513×257网格在时间步长为T/4 000时的升沉力时均功率误差小于0.5%.另外,定义升沉力改变方向的时间与升沉运动改变方向的时间之间的差值为HFL.当HFL的数值为正值时,表示升沉力比升沉运动滞后改变方向;当HFL的数值为负值时,表示升沉力比升沉运动提前改变方向.从表1的结果可见:本算法中扑翼升沉力改变方向的时间滞后于其升沉运动改变方向的时间;采用2×257×129网格在时间步长为T/2 000时计算得到的结果与2×513×257网格且时间步长为T/4 000时得到的结果相近.这表明在接下来的模拟中采用2×257×129网格就能保证数值结果的准确性.

使用S-A湍流模型的二维计算所得到的升沉力系数在一个周期内的变化情况与实验结果十分接近.因此计算的可靠性和可信性都得到了很好的验证(见图7(d)).

4 结果与分析

4.1 俯仰波形对获能效率的影响

在θ0=76.3◦,St=0.879 6,βt=1.13时满足获能的必要条件(见式(12)),给出了βr分别取0.5,1.0和4.0时所对应的3种不同俯仰波形的扑动的升沉力系数、俯仰力矩系数、无量纲的升沉速度、无量纲俯仰角速度以及实际来流攻角在一个运动周期内的变化情况(见图8).

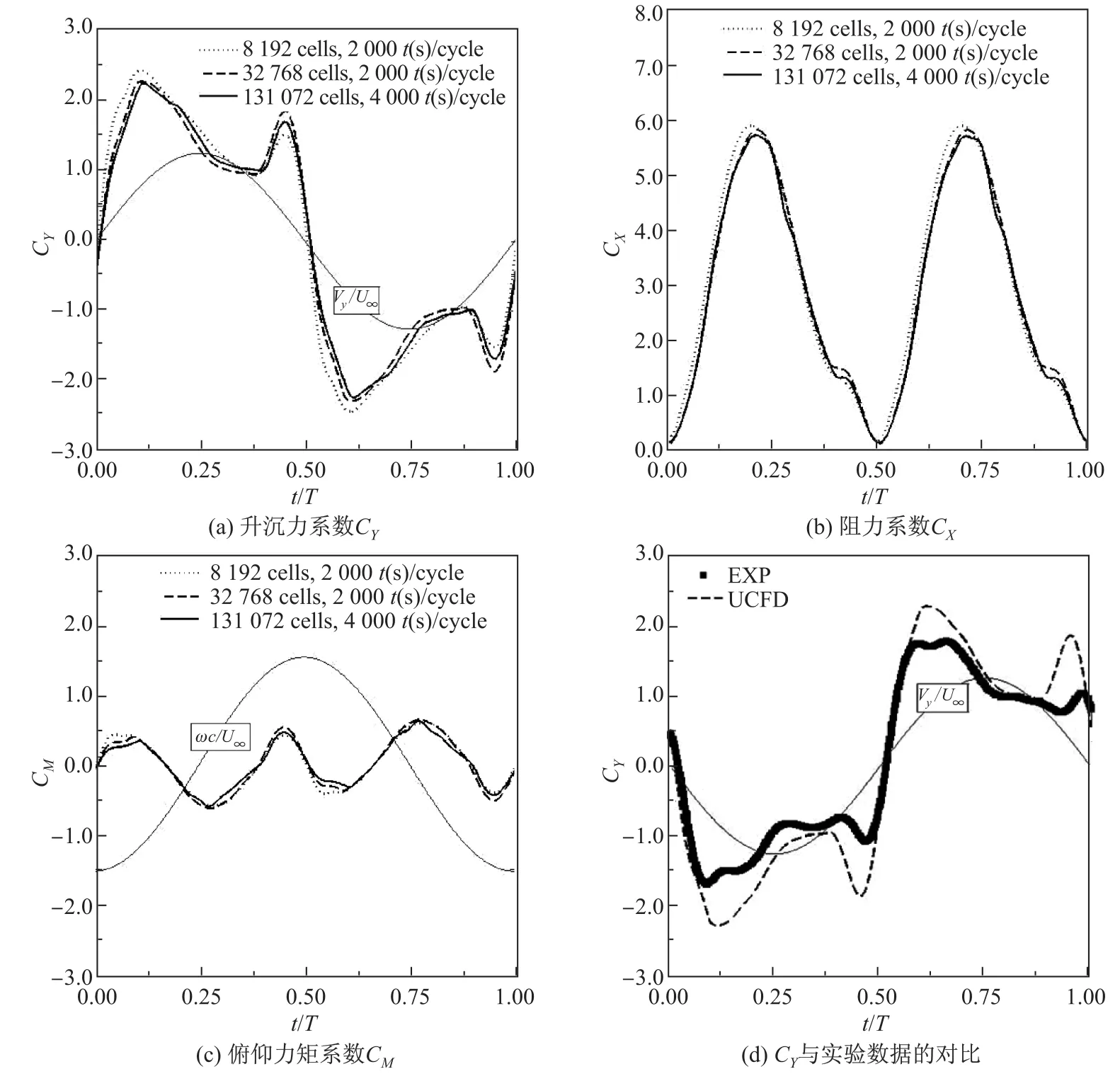
图7 网格和时间步长验证及实验对照Fig.7 Time steps and grid independent veri fi cation and validation with experimental results

表1 不同网格和时间步长得到的时均功率系数Table 1 Statistics of power coefficients for di ff erent grids and time steps

4.1.1 矩形波俯仰

当βr=0.5时,俯仰运动的时间波形近似矩形波.每半个周期的开始时刻升沉力出现很大的峰值(绝对值最大),升沉力与升沉运动在每半个周期的末尾出现了不同步现象(见图8(a)),升沉时均功率系数比较低,为0.871,俯仰力矩则几乎完全与俯仰运动不同步作负功(见图8(d)),俯仰时均功率为-0.339(见表2).

4.1.2 正弦波俯仰

当βr=1.0时为正弦波俯仰,升沉力、俯仰力矩和扑动运动几乎都保持了同步性(见图8(b)和(e)),升沉力时均功率较高,为0.937,俯仰运动也有做功(见表2).

图8 当θ0=76.3◦,St=0.879 6,βt=1.13时,在一个运动周期内各无量纲量的变化情况Fig.8 Time evolutions of non-dimensional values in a cycle for di ff erent βrwith θ0=76.3◦, St=0.879 6,βt=1.13

表2 对应图7三种情况的时均功率系数Table 2 Mean power coefficients for the three cases of Fig.7

4.1.3 三角波俯仰

当βr=4.0时,俯仰运动的时间波形近似三角波,升沉力与升沉运动的同步性较好(见图8(c)),但是俯仰力矩与俯仰运动也有不同步现象且做负功(见图8(f)),俯仰时均功率为-0.082(见表2).

图9给出了以上三种情况在0.38T时刻(此时出现了矩形波俯仰)的涡量云图.可以发现,在矩形波俯仰情况(βr=0.5)下尾缘生成的负涡影响到了从前缘脱落下来的正涡(前缘涡),造成了矩形波俯仰的前缘涡较其他两种情况的强度低,离开翼面的距离远.这说明俯仰运动方式改变了涡的生成以及与翼型的相互作用,进而影响了扑翼受到的作用力.

4.2 升沉波形对获能效率的影响

当θ0=76.3◦,St=0.666,βr=1.0时,给出了βt取1.00,1.55和1.98时所对应的3种不同俯仰波形的扑动的升沉力系数、俯仰力矩系数、无量纲的升沉速度、无量纲俯仰角速度以及实际来流攻角在一个运动周期内的变化情况(见图10).可见,随着βt的增大,升沉运动的时间波形从余弦波逐渐改变为矩形波,但这3个不同的βt得到的升沉力系数和俯仰力矩系数的大小和时间规律比较接近,且与各自的分运动保持了良好的同步性,其获能效率也大体相近,都在35%左右.

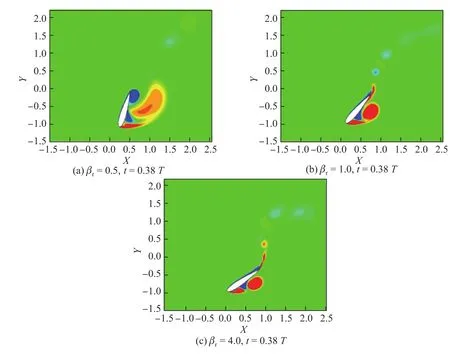
图9 不同俯仰波形扑动获能在相同时刻的涡量云图Fig.9 Contours of vorticity for di ff erent βr

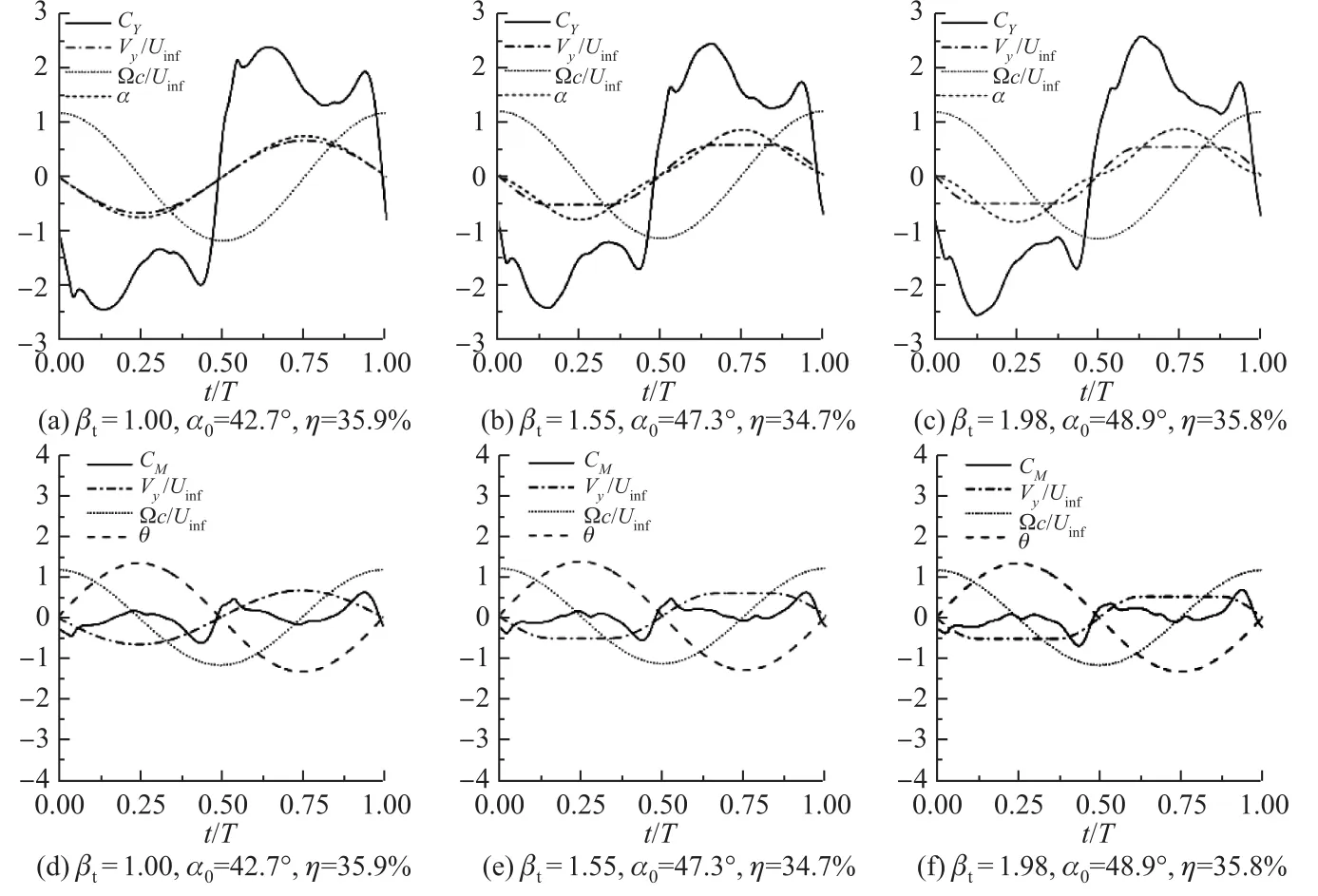
图10 θ0=76.3◦,St=0.666,βr=1.0时,在一个运动周期内的各个无量纲量变化情况Fig.10 Time evolutions of non-dimensional values in a cycle for di ff erent βtwith θ0=76.3◦, St=0.666,βr=1.0

由以上的分析比较可以看出,俯仰运动的波形对扑动获能有较大的影响,而升沉运动的影响有限.因此对St和θ0等参数进行分析时,固定βt值为1.13,仅改变βr的取值.

4.3 St,θ0和α0对获能效率的影响

由功率公式可知,St决定了无量纲升沉运动的幅值,St越大则做功能力越大(见图11).当St固定为0.879 6时,俯仰幅值θ0=76.3◦时的扑动获能的效率最高(见图12).

图11 当θ0=76.3◦,βt=1.13时的效率曲线Fig.11 Efficiency curves with θ0=76.3◦,βt=1.13

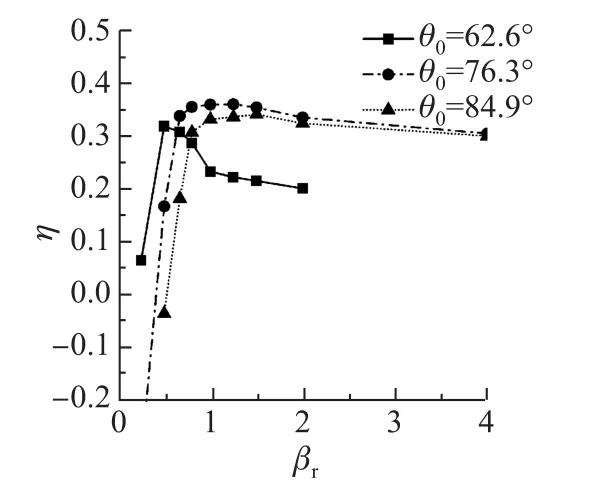
图12 当St=0.879 6,βt=1.13时的效率曲线Fig.12 Efficiency curves with St=0.879 6,βt=1.13

实际来流攻角α作为准则建立的依据,是扑动获能的重要指标.较大的实际来流攻角幅值α0对应的获能效率也较高(见图13).

图13 当χ=1时不同α0获能效率随βr的变化Fig.13 Efficiency curves for di ff erent α0and βrwith χ=1

图14给出了θ0分别取76.3◦和45.0◦,St分别取1.332和0.393,βt和βr分别为1.13和0.67时的升沉力系数变化曲线.可以看出,虽然两种运动方式的α0相差很小,分别为25.0◦和24.8◦,但是两种情况的升沉力系数有较大的差别,半周期平均升沉力系数为1.9和1.3,因此非定常流动的受力仅仅通过来流攻角是无法预测的.

图14 实际来流攻角几乎相同的两种运动方式的升沉力系数变化曲线Fig.14 Time evolutions of plunging force coefficients and other non-dimensional values in a cycle with attack angle almost the same at every moment

通过以上的计算结果发现,当St=1.332,θ0=76.3◦,βt和βr分别为1.13和0.67时,扑动获能的效率最高,为41%.

4.4 俯仰轴对获能效率的影响

以上结果的俯仰转轴都位于距前缘1/3处.为了研究俯仰转轴的位置对获能的影响,对获能效率较低的βr=0.5的俯仰轴位置由距前缘1/3弦长处移动到距前缘1/2弦长处.结果发现,俯仰轴后移使得升沉力系数的峰值出现时间有了较大的变化,与运动的同步性也有了很好的改善(见图15),获能效率提高了将近一倍.

图15 不同俯仰轴位置的升沉力系数和俯仰力矩系数Fig.15 Time evolutions of plunging force coefficients and pitching moment coefficients for cases with di ff erernt pitching axis

5 结束语

运用数值模拟方法研究了扑翼不同波形的升沉俯仰运动,发现俯仰运动波形对扑翼的升沉力、俯仰力矩及与之对应的分运动的同步性有很大的影响.升沉运动的波形在准则所限定的范围内对力与运动的同步性影响很小.

St数是表征扑翼升沉运动幅值的指标,St越大表示扑翼升沉运动的做功能力就越强.在一定的St下存在一个最佳的俯仰幅值θ0,可以使扑翼具有最高的获能效率.俯仰轴位置对升沉力和俯仰力矩的影响很大,对力与运动的同步性影响也很大.

对于俯仰轴位于距其前缘1/3弦长处的扑翼,当St=1.332,θ0=76.3◦,βt和βr分别为1.13(此时的俯仰波形为接近正弦波)和0.67时,扑动获能的效率最高,为41%.

[1]MCKINNEY W,DELAURIER J.Wingmill:an oscillating-wing windmill[J].Journal of Energy, 1981,5(2):109-115.

[2]JONES K D,PLATZER M F.Numerical computation of fl apping-wing propulsion and power extraction[J].AIAA Paper,1997,97:0826.

[3]JONES K D,LINdSEY K,PLATZER M F.An investigation of the fl uid-structure interaction in an oscillating-wing micro-hydropower generator[J].Advances in Fluid Mechanics,2003,36:73-84.

[4]KINSEY T,DUMAS G.Parametric study of an oscillating airfoil in a power-extraction regime[J]. AIAA Journal,2008,46(6):1318-1330.

[5]XIAO Q,LIAO W,YANG S.How motion trajectory a ff ects the energy extraction performance of an oscillating foil?[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.2010:1-16.

[6]ASHRAF M A,YOUNG J S,LAI J C,et al.Numerical analysis of an oscillating-wing wind and hydropower generator[J].AIAA Journal,2011,49(7):1374-1386.

[7]黄典贵.一个通用统一的流体力学计算软件及其考核[J].工程热物理学报,2012,33(10):1699-1702.

[8]黄典贵.统一的对流扩散型可压缩流体力学方程与解法[J].工程热物理学报,2007,27(3):391-394.

[9]黄典贵.一种新的流体力学预处理方法[J].工程热物理学报,2005,26(4):593-595.

[10]KINSEY T,DUMAS G.Computational fl uid dynamics analysis of a hydrokinetic turbine based on oscillating hydrofoils[J].Journal of Fluids Engineering,2012,134(2):021104.

[11]SIMpSON B J,HOVER F S,TRIANTAFYLLOU M S.Experiments in direct energy extraction through fl apping foils[C]//Proceedings of the Eighteenth International O ff shore and Polar Engineering Conference.2008:370-376.

本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn

Numerical simulation on energy acquisition of fl apping airfoil with di ff erent forms of movement

HAN Wei1,SUN Xiao-jing2
(1.Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University, Shanghai 200072,China; 2.School of Energy and Power Engineering,University of Shanghai for Science and Technology, Shanghai 200093,China)

Airfoil fl apping in wind or water fl ow can be either propulsion or power extraction.This study uses waveform parameters to control the fl apping motion.Unsteady numerical simulation is performed to study the e ff ect of St number,amplitude and waveform of heave pitch motion on its energy extraction efficiency.The in fl uence of di ff erent positions of pitching axis on the power extraction efficiency is also studied.The results show that the waveform-parameter and pitching axis location have a great in fl uence on the fl apping wing for power extraction in the parameter domain.Contrarily,the in fl uence of waveform of heave motion is limited.When St is 1.332,θ0is 76.3◦,and both βtand βrare 1.13(making the pitch waveform close to a sine wave)and 0.67 respectively,the fl apping airfoil can extract power at the highest efficiency,which is 41%.

wind energy(water stream energy)acquisition; fl apping airfoil;motion forms; unsteady numerical simulation

TK 89

A

1007-2861(2015)04-0432-12

10.3969/j.issn.1007-2861.2014.02.009

2014-01-10

国家自然科学基金资助项目(50836006,11202123)

孙晓晶(1976—),女,博士,研究方向为新能源中风能及潮流能应用技术.E-mail:xjsun@shu.edu.cn