基于改进模拟退火算法的LUT逆半调模板选择

卢永乐，文志强，李建飞

（湖南工业大学计算机与通信学院，湖南株洲412007）

基于改进模拟退火算法的LUT逆半调模板选择

卢永乐，文志强，李建飞

（湖南工业大学计算机与通信学院，湖南株洲412007）

针对影响LUT逆半调图像质量的模板选择问题，提出了一种基于改进模拟退火算法求取最优LUT逆半调模板算法。该算法能对灰度图像逆半调，还扩展至彩色图像逆半调。彩色图像逆半调时，充分考虑彩色图像R,G,B 3通道之间的相关性，将单通道模板扩展为3通道。实验结果表明：本算法寻得的模板具有全局最优性；与传统模板选择算法相比，利用本算法对灰度图像和彩色图像进行逆半调的结果图在人眼视觉效果上更佳，平均峰值信噪比更高。

逆半调；模拟退火算法；模板选择；查找表；彩色图像

0 引言

半调是一种将连续色调图像编码为二值图像等观感半色调图像）的技术[1]。由于人眼视觉的低通滤波特性，在一定视觉距离外，人眼观测到的半调图像会与原始连续色调图像相近[2-3]。因此，半调技术被广泛应用于图像的打印、印刷、显示等领域，其可降低图像的再现成本，还解决了某些打印、显示设备只能处理黑白二值图像的问题。从原始连续色调图到半调二值图是多对一映射关系，半调操作是对原始像素值进行二值量化，而这样引入了量化噪声，因此，半调过程是图像退化的过程[4]。

逆半调是半调的逆过程，即将二值半调图重建为连续灰度图。如果直接对二值半调图像进行图像放大、压缩、增强等操作，则会降低图像质量，因此，需对其进行逆半调操作。由于图像逆半调是一对多的映射过程，因此半调图像无法完美重建。目前，逆半调技术主要分为3类：滤波法、最优化估值法与机器学习法。其中，滤波法包括高斯低通滤波法、小波变换、FIR（finite impulse response）滤波、非线性滤波技术等[5]。滤波法主要考虑半调噪声在图像中的分布情况，滤除中、高频噪声，但低通滤波法在滤除噪声的同时，图像的边缘和细节信息也会损失，使图像变得模糊。小波变换能够很好地保留边缘与细节信息，但需要进行三层平稳小波变换，其算法的空间、时间复杂度高[6]。最优化估值法包括近似迭代、MAP（maximum a posteriori）估计、POCS（projection onto convex sets）估计、ED（error diffusion）核估计法等。最优化估值法要求半调误差分散核已知或需要根据一定的先验知识，而在实际应用中很难获得误差分散核，且先验知识较为复杂[1]，因此，基于估值算法的操作难度较高。

LUT（look-up table）逆半调是一种通过查找索引表来完成图像重建的方法，是一种典型的机器学习方法，通过分析半调图像与连续色调图之间的统计特征，生成一组从半调模式到逆半调值的映射表。该算法无需任何线性滤波器，对半调图像的半调类型无任何要求，具有通用性。该算法只需对训练集进行一次训练、建表，且逆半调过程中只进行查表操作，将当前像素值替换成连续值，而不涉及任何复杂的滤波计算，因此，其处理速度明显优于其它算法，并且能够得到较好的图像重建效果。

LUT模板的大小、形状以及如何对模板进行分块直接影响了图像的重建质量。近几年，国内外研究学者提出了多种改进的LUT逆半调算法，如利用图像纹理信息、神经网络等。而对直接影响LUT逆半调质量的模板选择问题却很少研究。2001年 M. Mese等[9]提出了一种基于贪心算法的LUT模板选择方法。自此，LUT模板的选择一直沿用该方法，但该方法并不能求得全局最优模板，存在一定缺陷。本文针对选择最佳LUT模板问题，提出了基于改进模拟退火算法的LUT逆半调最优模板选择算法，以提升LUT逆半调质量。

1 LUT逆半调算法的基本思想

LUT逆半调算法的基本思想是：以一组原始连续图像及其对应的半调图像作为训练集，以固定的LUT模板遍历半调图像及其对应的连续图，遍历过程中半调图像LUT模板中的邻域像素值与原始图像中当前像素点的连续值对应，从而建立索引表，原理如图1所示。图中，半调图的LUT模板，a表示的像素点，O表示中心像素点；LUT映射表中，索引值为LUT模板的半调值（0或1），该索引值对应的当前连续值即为逆半调值。

图1 LUT逆半调算法思想示意图Fig.1 Schematic diagram of LUT inverse halftone algorithm

LUT逆半调分为2个阶段，即建表阶段和逆半调阶段。

1）建表阶段。初始化LUT[]=0,N[]=0，LUT[]用于存储半调模式值到多级连续值的映射表，N[]用于存储同一半调值所对应不同多级连续值的个数。选择合适的LUT模板（图1为传统rect-16邻域模板）对每对半调图像及其连续色调图像按照从左至右、从上至下的顺序进行滑动，提取半调模式与其对应连续色调值，并将其记录于LUT表中，即N[i]=N[i]+1,LUT[i]=LUT[i]+g[i]，其中i为一串二进制数值， 即训练模板在半调图像中所对应的像素值。训练完成后，执行LUT[i]=LUT[i]/N[i]，并进行空值估计。

2）逆半调阶段。采用与建表时相同的LUT模板对半调图进行遍历，将LUT[i]取代当前像素值。

LUT逆半调算法主要受3个因素影响：训练样本数量、空值估计的准确度和LUT模板。训练样本的数量影响了LUT表的空值率，空值是指在逆半调过程中遇到了训练样本中从未出现过的半调模式值，即没有连续色调值与其索引值对应。无限增大训练样本数量并不能确保空值不出现，反而增加了训练时间，因此，应适当选取训练样本数量。空值估计可以解决查找表中出现的空值问题，是根据查找表中的邻近值或其它数学特征确定该索引值对应的连续值的方法。对于空值估计算法，国内外已有一些研究，如高斯低通滤波法、汉明距法和最佳线性估计法等。LUT模板的大小、形状以及如何对模板进行分块直接影响了图像的重建质量，国内外对LUT逆半调的改进研究中大多结合纹理信息、模式识别等。而对直接影响LUT逆半调质量的模板选择问题研究较少，因此，本文针对如何选择最佳LUT模板，提出了一种全局最优模板选择算法。

2 改进模拟退火算法与LUT逆半调模板选择

模拟退火算法是一种全局优化算法，在局部搜索过程中引入了随机扰动机制[7]。与贪心算法相比，模拟退火算法是以一定的概率接受一个比当前解要差的解，因此，有可能跳出局部最优到达全局最优解。与遗传算法相比，采用模拟退火算法求取LUT逆半调模板可以避免遗传算法“过早收敛”的缺陷，即由于优良个体急剧增加使种群失去了多样性，从而进化个体过早成熟，达不到全局最优解。但直接使用传统的模拟退火算法求取LUT逆半调最佳模板存在以下缺点：

1）初始温度值的确定和温度下降幅度的控制较难。如果设置的初始温度值太大，则退火时温度下降速度很慢，虽然这样能够得到最好解，但是搜索时间较长。反之，则会出现搜索过早结束，无法找到全局最优模板。

2）在寻找最优解的过程中，模拟退火算法是以一定的概率接受较差的解，这是该算法全局寻优的关键，然而，该环节可能把当前的最优解忽略掉，这样既浪费了搜索时间，又影响了求解效果。

本文针对LUT逆半调模板的最优化选取问题，提出了一种结合改进模拟退火算法寻求最优模板的方法。模拟退火算法的改进如下：

1）设计具有自适应功能的温度更新函数。如果某一温度下的状态被接受的次数较多，这时可以加大温度的下降幅度。反之，则减小温度的下降幅度。

2）搜索过程中增加记忆功能。记住搜索过程中当前的最优解，并随着搜索的进行实时更新。

改进后的模拟退火算法是一种智能算法。

2.1 灰度图像LUT逆半调模板选择

利用改进后的模拟退火算法求最佳Npixel邻域LUT模板，部分操作如下。

1）状态编码及状态初始化。由于LUT最优模板的求解属于非连续值问题，因此首先需要对改进的模拟退火算法的状态（对应为LUT模板）进行编码。本文采用二进制编码，LUT模板的像素0表示该点未被选入模板，像素1表示该点被选入模板。规定LUT模板在一矩形框内，假定矩形框为N×N，每个编码中1的个数保证为Npixel个，即模板大小为Npixel个像素点。模板中心为当前待处理像素点，该点的值固定为1。初始化模板时，可将中心点置为1，其余位置随机置为0或1，但需保证模板中1的个数为Npixel个。例如：N=5,Npixel=1 6，则状态编码“1111111111111110111000100”对应的LUT模板如图2所示。图2为传统19邻域LUT逆半调模板，其中，1的位置可以在5×5框的任意位置，但需要保证中心点为1，且模板像素的大小（即1的个数）为16个。LUT模板用N×N二维数组存储。

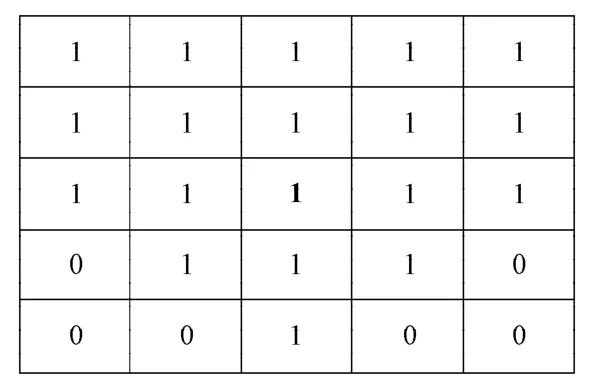
图2 状态编码示意图Fig.2 Schematic diagram of state coding

2）目标函数。LUT模板的优劣主要表现在逆半调图像质量的好坏。如仅针对某一半调图像的重建质量，则无法体现该模板的普适性。因此，选择对P幅半调图像进行逆半调处理，再计算该模板恢复的图像的平均峰值信噪比（peak signal to noise ratio，PSNR）。设计式（1）作为判断模板优劣的目标函数。

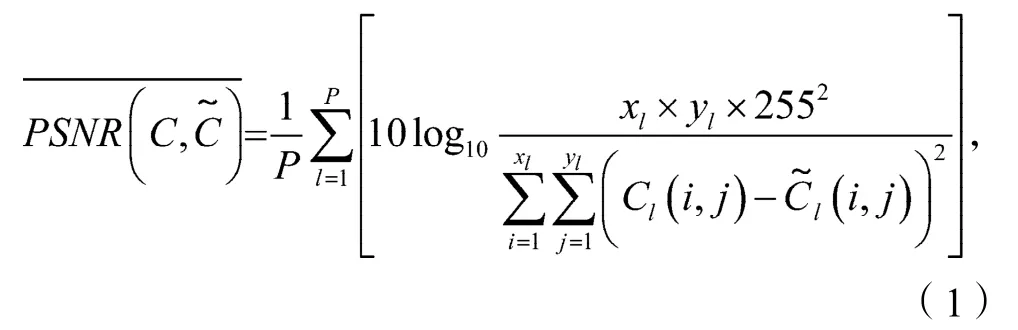
式中：xl,yl分别为第l（l=1,2,…,P）幅图像的高与宽；Cl(i,j)为第l幅连续色调图像在（i,j）处的像素值；为使用当前模板恢复的第l幅逆半调图像在（i,j）处的像素值。

3）新状态产生方式。在计算完当前状态的目标函数值后，需要对当前状态进行扰动，使其产生新状态。对于连续数值问题，可以选择临近值作为新状态。LUT模板属于离散组合问题，本文对新状态的产生按如下方式进行：在N×N大小的LUT模板框中随机选取一个像素，该点记为A（为方便逆半调操作，中心像素点不在选取之列）；如果A值为1（0），则再在模板中随机选取一个值为0（1）的像素，该点记为B；最后，将A,B 2点位置对换，产生新状态。

4）状态接收概率函数。状态接收概率函数用于判断新状态（即新LUT模板）被接受的概率。若新状态被接受，则将当前状态更新为新状态。本文以式（3）作为状态接收概率函数。

5）温度更新函数。设置初始化温度T0，温度按更新函数逐渐下降，最终达到稳定。根据当前温度下状态被接受的次数自动调节温度下降幅度，设计式（4）～（5）为温度更新函数。

式（4）～（5）中：为退火因子；N′为Tm温度下的内循环次数；n为当前温度下状态被接受的次数，0＜n≤N′。

基于改进的模拟退火算法求取LUT逆半调模板算法的具体步骤描述如下。

Step 1设定初始值：初始状态LUT0（即初始模板LUT0）、初始温度T0、终止温度Tmin、内循环次数N′。利用LUT0对P幅半调图像及其对应连续色调图像进行训练、建表，并对训练集中的半调图像进行逆半调恢复。利用式（1）计算当前状态LUT0的目标函数值。

Step 2对当前状态LUT0进行扰动，产生新状态LUT1。按照Step 1中的计算方式，得到新状态的目标函数值。再利用式（2）得到ΔE。

Step 3通过式（3）得到P(ΔE)。当新状态被接受（即ΔE≥0且P(ΔE)＞r，其中，r为随机浮点数）时，则LUT0=LUT1=。

Step 4在当前温度下，重复N′次执行Step 2和Step 3，统计该温度下状态被接受的次数n。

Step 5根据式5缓慢降低温度。

Step 6重复Step 2～Step 5，直至温度T＜Tmin。

基于改进的模拟退火算法求取LUT逆半调模板的算法流程如图3所示。本算法的特点是：该算法增加了记忆功能，保存搜索过程中当前出现的最优模板，并与新状态进行对比，更新模板；内循环N′次的目的是，使选择模板达到该特定温度下的平衡；外循环中，随着温度的降低，较差解被接受的概率也会降低，当温度趋近于Tmin（本文Tmin为0）时，不再接受较差解，算法收敛到全局最优解。

图3 基于改进的模拟退火算法的最优LUT逆半调模板选择算法流程图Fig.3 The flowchart for optimal LUT inverse halftoning template selection based on improved simulated annealing algorithm

2.2 彩色图像LUT逆半调模板选择

当前大多数逆半调算法主要是针对灰度半调图像，而较少涉及彩色半调图像[8]。由于彩色半调图像在R,G,B 3通道的噪声和边缘并非完全独立分离，单独分析某一通道割离了彩色图像的整体性，因此，采用针对灰度图像的逆半调算法对彩色半调图进行逆半调的效果不佳。考虑彩色图像各通道之间具有高度相关性的特点，本文提出了改进的彩色图像LUT逆半调算法。在LUT训练、建表、逆半调恢复阶段，通过综合考虑彩色图像R,G,B 3通道的像素，预测彩色逆半调图中某一特定通道的连续色调值。

本算法先要确定利用哪些彩色通道的哪些像素对当前通道的像素进行逆半调恢复，即明确LUT模板的形式及模板中像素点的分布。将单通道的LUT模板扩展至R,G,B 3通道，逆半调重建X通道（即R或G或B通道），需用到一个N×N×3的模板，N为模板所处的矩形框大小。例如：对R通道进行逆半调，可用图4所给出的19邻域LUT模板，该邻域包括了G,B通道，对G,B通道进行逆半调时，也是采用图4的LUT模板。因此，该算法除需遍历3通道外，不会加大LUT逆半调算法的时间复杂度。

图4 R通道的19邻域LUT逆半调模板示例Fig.4 Example of R channel 19 neighborhood LUT inverse halftone template

为了得到最佳彩色逆半调LUT模板，本文在前述的改进模拟退火算法求取LUT最佳模板算法的基础上进行改进。

1）模板像素的选取及中心点的确定。初始状态的产生方式是在N×N×3的矩形框任意位置选取Npixel个像素作为LUT模板像素（需保证中心点为被选之列）。若求取X通道的最佳LUT逆半调模板，则设定模板的中心点为N×N×3矩形框中X通道的中心位置（即第3行第3列）。

2）新状态的产生方式。在N×N×3的LUT模板框中随机选取2个像素，分别记为A,B（中心像素点不在选取之列）。如果A点位置值为1（0），则再在模板中随机选取一个值为0（1）的像素点（B点和中心点除外），该点记为C，将A,C 2点位置对换。同理，如果B点位置值为1（0），则再在模板中随机选取一个值为0（1）的像素点（A点、C点和中心点除外），该点记为D，将B ,D 2点位置对换，新状态产生。该方式旨在加速退火算法的搜索速度，更快接近最优解。

该算法在训练、建表、逆半调时，均按照模板考虑3个通道的邻域像素，充分利用了彩色图像3通道之间的相关性。实验结果证明了该方法恢复的彩色逆半调图像具有较好的去噪效果，较高的重建质量，恢复的色彩给人眼视觉效果较好。

3 实验结果分析

为验证利用改进模拟退火算法求取最佳LUT模板算法的有效性，本文在VS 2010和Matlab 7.0环境下进行了实验验证。由于训练样本的数量和内容会影响实验结果，因此本实验的训练样本来源于网络http://pan.baidu.com/s/1bnGkLqf图像库。

3.1 灰度图像逆半调实验

进行灰度图像逆半调实验时，选用图像库中的60幅512×512的连续色调图及其对应采用Jarvis,Stucki,Floyd-Steinberg算法产生的误差分散半调图。将本文算法与文献[9]中的传统模板选择算法分别对灰度图像进行逆半调，计算60幅逆半调图像的平均峰值信噪比[10]。本文算法的参数设置如下：T0=100 000，Tmin=1，N′=40，P=60，N=5，Npixel=19。实验求得的LUT模板如图5～7所示。

图5 Floyd-Steinberg最佳19邻域LUT模板Fig.5 Floyd-Steinberg 19 neighborhood optimal LUT template

图6 Jarvis最佳19邻域LUT模板Fig.6 Jarvis 19 neighborhood optimal LUT template

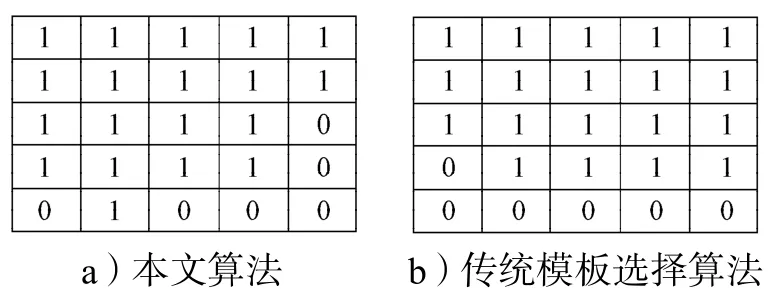
图7 Stucki最佳19邻域LUT模板Fig.7 Stucki 19 neighborhood optimal LUT template

2种算法分别对60幅半调图像进行逆半调的平均峰值信噪比如表1所示。分析表1中的数据可知，对3类误差分散半调图像进行逆半调，本文算法求得的LUT模板的PSNR效果比传统模板选择算法的更好。这说明了本文算法比传统模板选择算法优越。

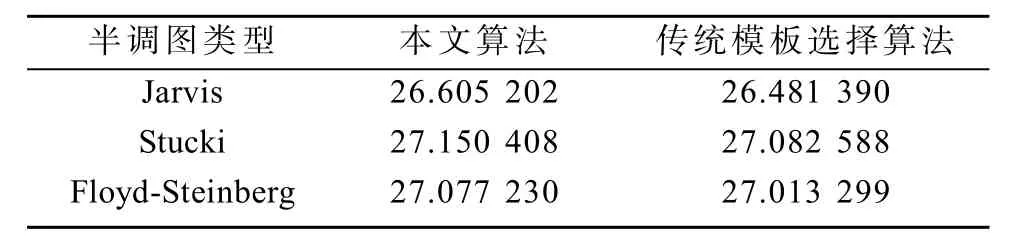
表1 模板优劣性对比表Table 1Comparison of different templates

对2种算法进行了测试，比较逆半调效果，即对由Floyd-Steinberg误差分散算法产生的Lena和Pepper 2幅半调图进行逆半调，效果图如图8～9所示。本文模板逆半调恢复Lena与Pepper半调图的峰值信噪比分别为32.125 500,31.812 700，而采用传统模板选择算法逆半调恢复Lena与Pepper半调图的峰值信噪比分别为31.398 000，30.741 900。可见，本文算法比传统模板选择算法的峰值信噪比更高，且人眼视觉上逆半调图像的边缘细节恢复更好。

图8 2种算法对Lena半调图的逆半调结果图Fig.8 Lena Inverse halftoning results produced by 2 different algorithms

图9 2种算法对Pepper半调图的逆半调结果图Fig.9 Pepper Inverse halftoning results produced by 2 different algorithms

3.2 彩色图像逆半调实验

彩色图像逆半调实验时，本文选取了70幅256× 256的彩色半调图（由Floyd-Steinberg算法产生）及其对应的逆半调图。本文算法参数设置如下：T0=100 000,Tmin=1,N′=40,P=70,N=5,Npixel=19。利用本文算法求得的彩色图像最佳19邻域LUT逆半调模板如图10～12所示。

利用传统19邻域模板（见图2）与本文的彩色图像最佳LUT模板对Orange,Little Girl 2幅彩色半调图像的逆半调结果如图13～14所示。

图10 R通道LUT模板Fig.10 LUT template for R channel

图11 G通道LUT模板Fig.11 LUT template for G channel

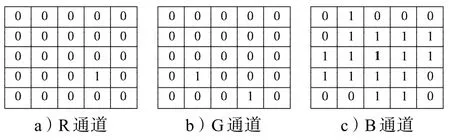
图12 B通道LUT模板Fig.12 LUT template for B channel

图13 2种算法对彩色Orange半调图的逆半调结果图Fig.13 Color orange inverse halftoning results produced by 2 different algorithms

图14 2种算法对Little Girl彩色半调图的逆半调结果图Fig.14 Little girl color inverse halftoning results produced by 2 different algorithms

利用本文模板对Orange,Little Girl彩色半调图进行逆半调的峰值信噪比分别为27.070 400,25.119 600，而传统19邻域LUT模板对Orange,Little Girl彩色半调图进行逆半调的峰值信噪比分别为26.762 500和24.743 100。可见，与传统19邻域LUT模板相比，利用本文LUT模板对半调图进行逆半调，结果图给人眼视觉上的效果更好，色彩还原效果更真实。

4 结语

本文针对影响LUT逆半调质量的重要因素—模板选择问题进行了研究，提出了一种基于改进模拟退火算法的最佳LUT模板选择算法，同时，将该算法进一步应用到彩色图像LUT逆半调中，充分考虑彩色像素3通道间的高度相关性，对彩色LUT模板进行了创新设计，使其扩展到3通道。由于模板邻域像素数量保持不变，因此不会增加查找表的空间存储量及逆半调操作的时间复杂度。本文算法对灰度图像和彩色图像进行逆半调恢复的图像质量都能达到令人满意的效果。

参考文献：

[1]孔月萍. 图像逆半调及其质量评价技术研究 [D]. 西安：西安电子科技大学，2008. Kong Yueping. A Study of Inverse Halftoning and Quality Assessment Schemes[D]. Xi’an：Xidian University，2008.

[2]Liu Yunfu，Guo Jingming，Lee Jiann Der. Inverse Halftoning Based on the Bayesian Theorem[J]. IEEE Transactions on Image Processing，2011，20(4)：1077-1084.

[3]姚莉. 数字半调技术及其评价方法研究[J]. 计算机工程与应用，2010，46(3)：4-8.Yao Li. Review on Digital Halftoning and Quality Assessment Schemes[J]. Computer Engineering and Applications，2010，46(3)：4-8.

[4]黄丽君，文志强，胡柳. 一种基于 LUT 的图像逆半调改进算法[J]. 计算机技术与发展，2013，23(6)：35-37.Huang Lijun，Wen Zhiqiang，Hu Liu. An Improved Image Inverse Halftoning Algorithm Based on LUT[J]. Computer Technology and Development，2013，23(6)：35-37. [5]Huang Y H，Chung K L，Dai B R. Improved Inverse Halftoning Using Vector and Texture-Lookup Table-Based Learning Approach[J]. Expert Systems with Applications，2011，38(12)：15573-15581.

[6]Xiong Z，Orchard M T，Ramchandran K. Inverse Halftoning Using Wavelets[J]. IEEE Transactions on Image Processing，1999，8(10)：1479-1483.

[7]张德富，彭煜，朱文兴，等. 求解三维装箱问题的混合模拟退火算法[J]. 计算机学报，2009，32(11)：2147-2156. Zhang Defu，Peng Yu，Zhu Wenxing，et al. A Hybrid Simulated Annealing Algorithm for the Three-Dimensinal Packing Problem[J]. Chinese Journal of Computers，2009，32(11)：2147-2156.

[8]Zhong Yunfei，Fu Lujing，Zhou Tao. Based on Median Pyramid Transform of the Color Image Inverse Halftoning [J]. Applied Mechanics and Materials，2012，200：724-729.

[9]Mese M，Vaidyanathan P P. Look-Up Table(LUT) Method for Inverse Halftoning[J]. IEEE Transactions on Image Processing，2001，10(10)：1566-1578.

[10]冯起芹，曹小龙，单武扬，等. 印刷品水印图像的半色调算法比较[J]. 包装学报，2012，4(3)：34-38. Feng Qiqin，Cao Xiaolong，Shan Wuyang，et al. Comparison Study of Halftoning Algorithm for Printed Watermarking Image[J]. Packaging Journal，2012，4(3)：34-38.

（责任编辑：邓 彬）

Template Selection for LUT Inverse Halftoning Based on Improved Simulated Annealing Algorithm

Lu Yongle，Wen Zhiqiang，Li Jianfei
（School of Computer and Communication，Hunan University of Technology，Zhuzhou Hunan 412007，China）

In view of template selection problems which affected the LUT inverse halftone image quality,puts forward a solution to an optimal LUT inverse halftone template based on improved simulated annealing algorithm. The algorithm can be used for grayscale image inverse halftoning and is extended to color image. As for color image halftoning,the correlation between 3 channels of R,G,B color image is considered,and the template is extended from single to triple. The experimental result shows that the proposed algorithm finds template with global optimality,and compares with traditional template selection algorithm,the result picture adopting the optimal template for grayscale and color image inverse halftone restoraion gets better effect in human vision system(HSV) and the average peak signal to noise ratio is higher.

inverse halftoning；simulated annealing algorithm；template selection；look-up table；color image

TP393

A

1673-9833(2015)01-0076-07

2014-11-11

国家自然科学基金资助项目（61170102），湖南省自然科学基金资助项目（11JJ3070），湖南省教育厅科研基金资助项目（12A039）

卢永乐（1989-），男，湖南江永人，湖南工业大学硕士生，主要研究方向为数字图像处理，E-mail：luyongle520@163.com

10.3969/j.issn.1673-9833.2015.01.014