量子退相位通道中量子Fisher信息动力学

王国友，夏湘芳，彭柯铭，陈光伟

（湖南工业大学理学院，湖南株洲412007）

量子退相位通道中量子Fisher信息动力学

王国友，夏湘芳，彭柯铭，陈光伟

（湖南工业大学理学院，湖南株洲412007）

利用量子通道估计方法研究了纯退相位通道下，2个相互作用量子比特系统退相干率的量子Fisher信息的动力学演化。数值计算表明：量子Fisher信息总是先从0增加到某一最大值后迅速衰减，最后又减小到0；退相干率越大，导致量子Fisher信息越小和衰减到0的时间也越短；提高初始输入态的纠缠不能使最大量子Fisher信息得到提升。

量子Fisher信息；纠缠；量子通道估计；退相干率；纯退相位通道

0 引言

所有的量子系统都不可避免地和它们的环境相互作用，因而系统的动力学演化成为系统的一个重要特性[1-2]。在退相干环境下，物理量的动力学问题已引起许多学者的研究兴趣。他们在研究中发现许多有趣的特性，例如纠缠演化中出现的纠缠死亡现象[3]，量子关联演化中表现出的突变现象[4]等。

环境往往影响甚至破坏一个物理系统演化的进程，因而尽可能精确地估计环境噪音的影响显得尤为重要。量子通道估计是用来辨别未知噪音的方法之一，这种方法首先要制备一个作为量子通道的最优输入态，并且这个态携带了要被估计的通道参数，然后在与环境相互作用之后的输出态上进行某一量子态最优测量，从而达到有效估计这个参数的目的[1]。

正像经典估计理论中费舍尔（Fisher）信息的地位那样[5]，在量子估计理论和量子信息理论中，量子Fisher信息也是一个关键的量。量子估计的目的是要估计出标记量子系统参数的值，并提高分辨率的精度[1,6]。量子Fisher信息是描述一个量子态关于一个参数变化敏感性的量，它与决定最优测量界的量子Cramer-Rao不等式密切相关[7]。近年来，人们对退相干下的量子Fisher信息动力学的研究表现出浓厚的兴趣[8-14]。Sun Zhe等[11]发现，处于一个量子临界自旋链环境中的自旋-j系统，当环境达到临界点时，其量子Fisher信息几乎单调衰减；Ma Jian等[12]研究了退相干下，N个量子比特的GHZ态的量子Fisher信息的演化，表现出衰减和突变现象；Zhong Wei等[13]得到了不同量子通道下单个量子比特的量子Fisher信息的Bloch矢量表示的公式；V. Bu ek等[14]直接估计了一个量子比特的平均退相干率。

本文对处于退相干环境中的2个初始纠缠的量子比特进行退相干率参数的估计。对这2个量子比特组成的系统，2个量子比特的退相干可以看作一个量子通道。采用文献[1]和文献[14]中量子通道估计的方法，考虑量子Fisher信息的动力学演化来估计通道退相干率参数。

1 模型和理论

考虑2个初始纠缠的完全相同的相互作用的量子比特A和B，每个量子比特由一个激发态和一个基态构成的一个二能级系统描述[3]，而且假设2个量子比特A,B间相互作用强度为v，它们独立地和各自的环境相互作用导致局域退相干。研究系统见图1。

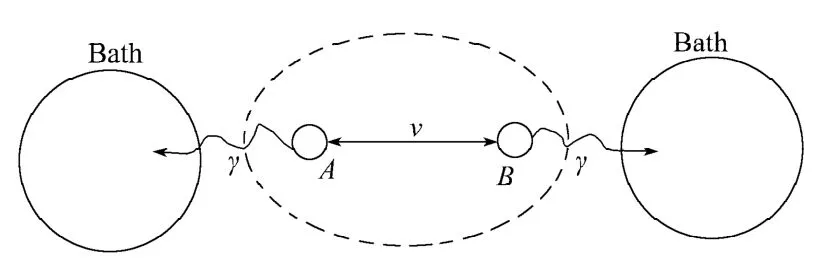
图1 研究系统示意图Fig.1 Schematic for the research system

研究系统模型的哈密顿量为（设h=1）

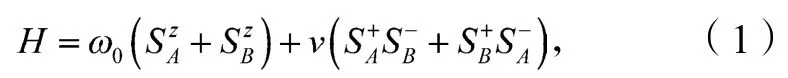
式中：0是原子的跃迁频率；

v是2个量子比特间的相互作用强度；

考虑每个量子比特的退相干通道是纯退相位通道，系统的动力学可由下列方程（2）描述。

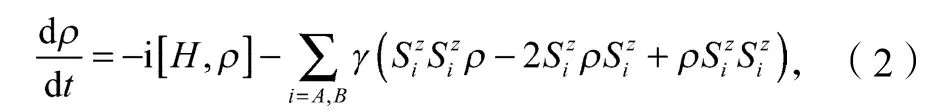
i为虚数单位；

为了研究退相干对参数估计精度的影响，需要研究2个量子比特的量子Fisher信息动力学。一个量子态关于参数的量子Fisher信息定义为

Tr表示求矩阵的迹。

如果一个量子态的谱分解为

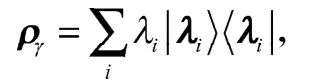
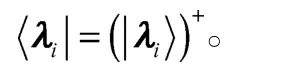
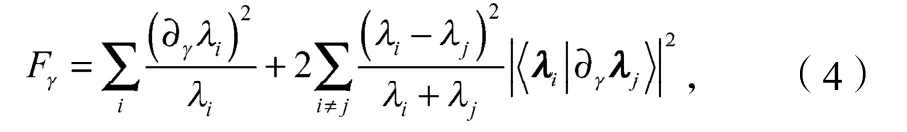
假设系统输入的初始态是一种X形混态

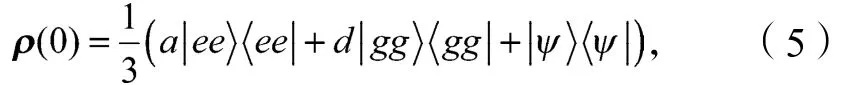
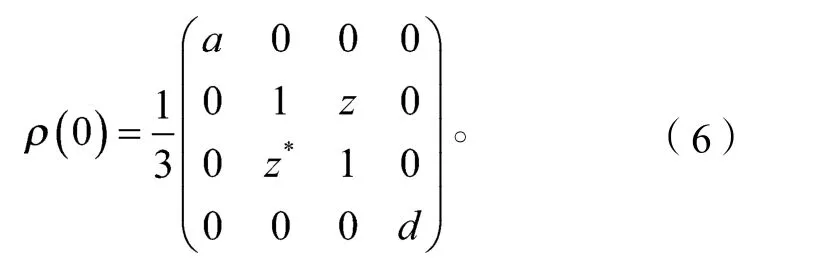
容易证明，在时间的演化中主方程（2）的解始终保持了X形，即

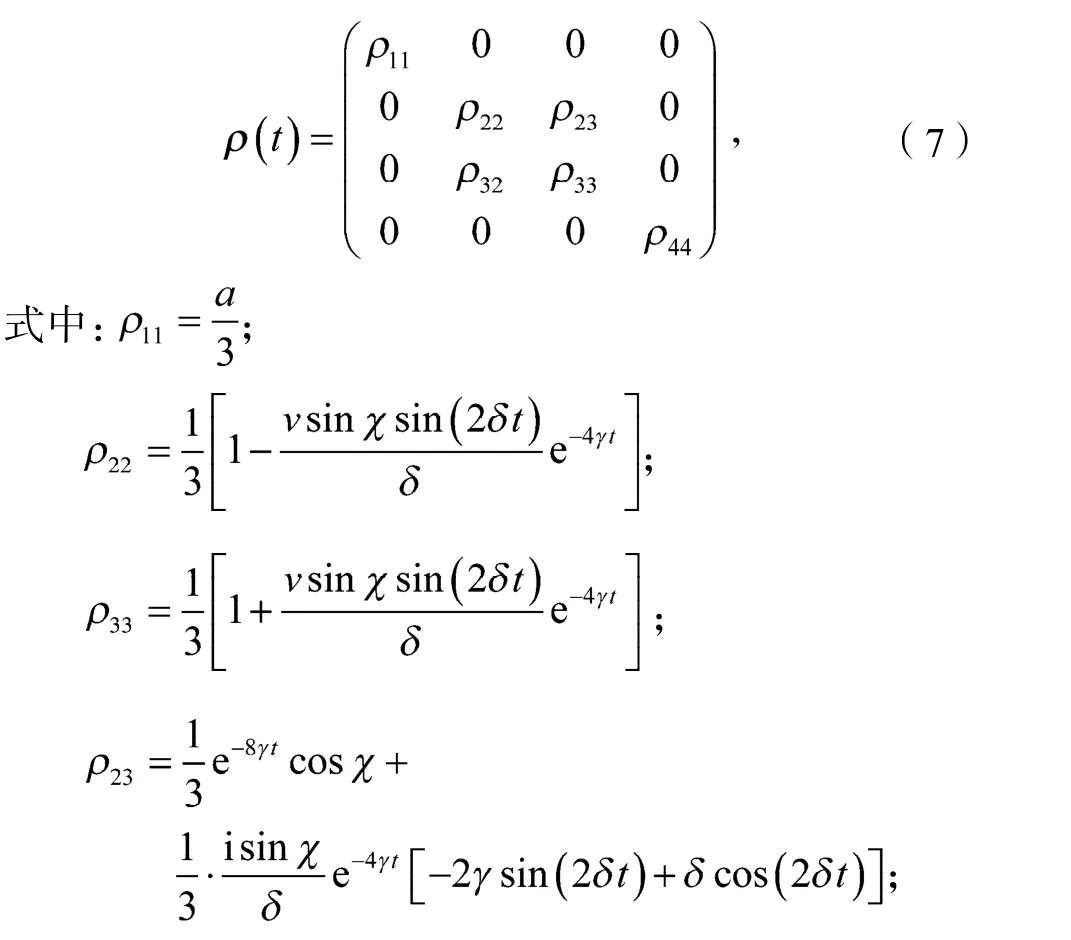
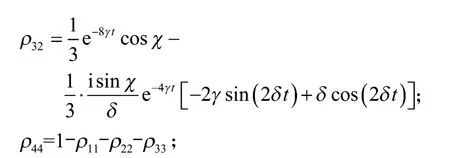
由于假设了2个量子比特的退相干率是相同的，并且把这种退相干看作一个量子通道，因而可以把2个量子比特作为一个整体来估计环境的退相干参数[1]，这就需要采用量子通道估计方法，研究量子Fisher信息动力学。通过对密度矩阵(t)对角化获得其本征值和对应的本征态，然后代入方程（4）得到量子Fisher信息的表达式。由于量子Fisher信息没有简单的解析式，下面以数值计算的形式给出的演化。

2 讨论

量子Fisher信息动力学演化见图2，图2给出了在a=0.5,v=0.8,=0条件下，2个相互作用的量子比特在纯退相位通道下，不同退相位率的量子Fisher信息动力学演化特性。

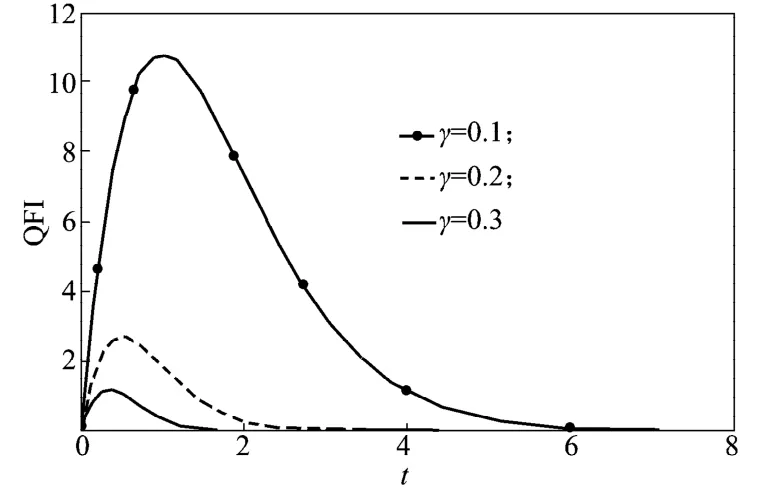
图2 量子Fisher信息动力学演化Fig.2 The dynamical evolution of the quantum Fisher information（QFI）

从图2中可以看出，对一个固定的退相位率，量子Fisher信息总是先从0增加到某一最大值后迅速衰减，最后减少到0。整个演化过程没有出现量子Fisher信息的突然死亡，也没有出现振荡行为。这在物理上可以理解为：在时间t=0时，由于处于激发态的原子还没有衰减，因而衰减率的量子Fisher信息是0。衰减开始时，原子处于激发态的概率大，衰减的可能性大，量子Fisher信息因此迅速增加。但随着不断衰减，处于激发的概率减小，量子Fisher信息也因此减小。最后，由于衰减使激发态概率变为0，量子Fisher信息也随即变为0。由于考虑的是马尔科夫环境，忽略了环境的记忆效应，因而没有出现振荡和复苏行为[9]。

从图2还可以看到，对不同的退相位率，退相位率越大，导致量子Fisher信息越小，达到最大值和衰减到0的时间也越短。这在物理上可理解为，退相位率大衰减就快，使原子处于激发态的概率迅速减小，从而使量子Fisher信息最大值减小并迅速变化为0[1]。

通常情况下，提高输入初始态的纠缠可以增大量子Fisher信息，也就可以提高参数估计的精度。如果用共生纠缠度来度量纠缠[3,15-16]，容易得到初始态的纠缠为

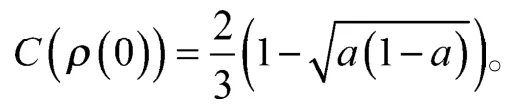
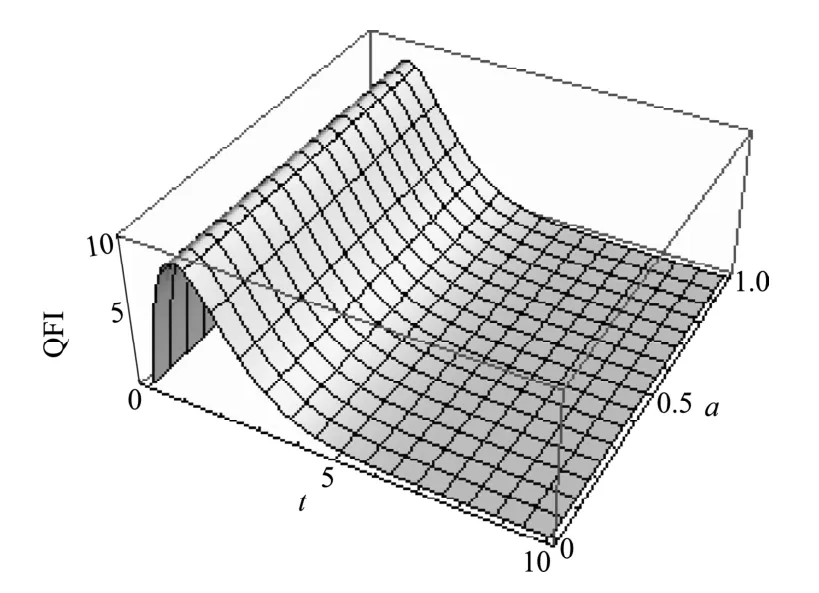
图3 参数a对量子Fisher信息动力学的影响Fig.3 The effect of parameter a on the dynamical evolution of the quantum Fisher information（QFI）

从图3可以看出，与文献[1]不同，这里不同的a值（对应不同的纠缠）对应着相同的最大量子Fisher信息，也就有相同的参数估计的精度。这说明提高输入态纠缠不总是可以提高参数估计的精度。

3 结论

本文利用量子通道估计方法，研究在纯退相位通道下，2个相互作用的量子比特系统的量子Fisher信息的动力学演化。数值计算表明，对不同衰减率的退相位通道，量子Fisher信息总是先从0增加到某一最大值后迅速衰减，最后减小到0。整个演化过程没有出现量子Fisher信息的突然死亡和振荡行为。而且衰减率越大，导致其量子Fisher信息越小，在演化中达到最大值和衰减到0的时间也越短。而且，提高输入态的纠缠可以提高量子Fisher信息的结论不总是正确的。至于量子纠缠和量子Fisher信息之间的关系问题值得进一步研究。

参考文献：

[1]Zheng Qiang，Yao Yao，Li Yong. Optimal Quantum Channel Estimation of Two Interacting Qubits Subject to Decoherence[J]. The European Phyical Journal D，2014. doi：10.1140/epjd/e2014-50047-1.

[2]Tsang Mankei. Quantum Transition-Edge Detectors[J]. Phys. Rev. A，2013. doi：10.1103/PhysRevA.88.021801. [3]Yu Ting，Eberly J H. Quantum Open System Theory: Bipartite Aspects[J]. Phys. Rev. Lett.，2006，97. doi：10.1103/PhysRevLett.97.140403.

[4]Fanchini F F，Werlang T，Brasil C A，et al. Non -Markovian Dynamics of Quantum Discord[J]. Phys. Rev. A，2010. doi：10.1103/PhysRevA.81.052107.

[5]Fisher R A. Theory of Statistical Estimation[C]// Proceedings of the Cambridge Philosophical Society. Cambridge：Cambridge Philosophical Society ，1925：700-725.

[6]Burgarth D，Maruyama K， Murphy M，et al. Scalable Quantum Computation via Local Control of Only Two Qubits[J]. Phys. Rev. A， 2010. doi：10.1103/PhysRevA. 81.040303.

[7]Holevo A. Probabilistic and Statistical Aspects of Quantum Theory[M]. Amsterdan：Springer，2011：221-225.

[8]Huelga S H，Macchiavello C，Pellizzari T，et al. Improvement of Frequency Standards with Quantum Entanglement[J].Phys. Rev. Lett.，1997. doi：10.1103/ PhysRevLett.79.3865.

[9]Berrada K. Non-Markovian Effect on the Precision of Parameter Estimation[J]. Phys. Rev. A，2013. doi：10.1103/ PhysRevA.88.035806.

[10]Lu Xiaoming，Wang Xiaoguang，Sun Changpu. Quantum Fisher Information Flow and Non-Markovian Processes of Open Systems[J]. Phys. Rev. A，2010. doi：10.1103/ PhysRevA.82.042103.

[11]Sun Zhe，Ma Jian，Lu Xiaoming，et al. Fisher Information in a Quantum-Critical Environment[J]. Phys. Rev. A，2010. doi：10.1103/PhysRevA.82.022306.

[12]Ma Jian，Huang Yixiao，Wang Xiaoguang，et al. Quantum

Fisher Information of the Greenberger-Horne-Zeilinger State in Decoherence Channels[J]. Phys. Rev. A，2011. doi：10. 1103/PhysRevA.84.022302.

[13]Zhong Wei，Sun Zhe，Ma Jian，et al. Fisher Information Under Decoherence in Bloch Repersentation[J]. Phys. Rev. A，2010. doi：10.1103/PhysRevA.87.022337.

[14]Bu ek V，Rapcan P，Rau J，et al. Direct Estimation of Decoherence Rates[J]. Phys. Rev. A，2012. doi：10.1103/ PhysRevA.86.052109.

[15]Wootters W K. Entanglement of Formation of an Arbitrary State of Two Qubits[J]. Phys. Rev. Lett.， 1998. doi：10. 1103/PhysRevLett.80.2245.

[16]Walborn S P，Souto Ribeiro P H，Davidovich L，et al.

Experimental Determination of Entanglement with a Single Measurement[J]. Nature，2006. doi：10.1038/nature04627.

（责任编辑：邓光辉）

Dynamics of Quantum Fisher Information Under Pure Dephasing Channel

Wang Guoyou，Xia Xiangfang，Peng Keming，Chen Guangwei
（School of Science，Hunan University of Technology，Zhuzhou Hunan 412007，China）

Using the quantum channel estimation method,studies the dynamical evolution of quantum Fisher nformation(QFI) with respect to decoherent rate of two interacting qubits under pure dephasing channel. Numerical results show that the quantum Fisher information always increases from zero to a maximum value before rapidly decays,finally decays to zero,a larger decoherence rate leads to smaller quantum Fisher information and shorter decay time to zero,and also show that the maximum quantum Fisher information is not enhanced by promoting the degree of entanglement in the nitial input state.

quantum Fisher information；entanglement；quantum channel estimation；decoherent rate；pure dephasing channel

O413

A

1673-9833(2015)01-0098-04

2014-10-20

湖南省教育厅科学研究基金资助项目（13C039）

王国友（1974-），男，湖南隆回人，湖南工业大学讲师，湖南师范大学博士生，主要研究方向为量子光学和量子信息，E-mail：gywang04@163.com

10.3969/j.issn.1673-9833.2015.01.018