单通道多分量伪码调制脉冲串信号分离及参数提取
2015-07-18张淑宁赵惠昌
朱 航 张淑宁 赵惠昌
①(南京理工大学电子工程与光电技术学院 南京 210094)②(解放军73015部队 湖州 313000)
单通道多分量伪码调制脉冲串信号分离及参数提取
朱 航①②张淑宁*①赵惠昌①
①(南京理工大学电子工程与光电技术学院 南京 210094)②(解放军73015部队 湖州 313000)
该文针对几种伪随机码调制脉冲串信号,包括伪随机二相编码(PRBC)脉冲串信号、伪随机脉位调制(PPM)脉冲串信号及伪随机脉位调制与伪随机二相编码复合(PRBC-PPM)脉冲串信号,为解决单通道多分量情况下的信号分离和参数提取问题,提出基于奇异值比谱和周期积累的载频及伪码波形估计方法。通过构建奇异值比谱估计广义周期并完成周期积累,再取平方进行FFT变换,并以去载频处理后信号的实部累加和为衡量标准,精确估计出载频并完成脉位波形估计。最后通过内积计算估计出幅度和初始相位。仿真与分析说明该文方法在不同信噪比下的有效性。
信号处理;单通道多分量信号;伪码调制脉冲串信号;参数提取;信号分离;广义周期
1 引言
战场侦察环境中由于信道资源有限,极有可能单通道内同时收到多个雷达引信信号,所以单通道参数估计与分离技术在这种情况下十分必要。对于雷达引信信号的单通道分离及参数提取,现今已有一些有效方法,如利用分数阶傅里叶变换实现参数提取[1,2],利用粒子滤波实现参数提取[3];利用自适应时频分布来实现信号分离[4];利用周期特点估计相应参数[5,6];利用周期模糊函数实现参数提取[7];利用谱相关方法估计参数[8]。上述方法针对连续波雷达引信信号能够达到较好的参数提取效果。脉冲串信号也是雷达引信系统当中常采用的信号,为提高其抗干扰性,采用随机信号对脉冲串进行调制是一种较好的方法,文献[9,10]介绍了随机脉位调制脉冲串信号,并对其特性及模糊函数进行了分析。然而由于不可复制性和实现困难,其应用受到一定限制,基于此可以利用伪随机码对脉冲串进行调制,该类信号具有周期性,容易实现且具有可复制性,保留了较高的抗干扰性能,在实际中得到较好的应用,在欧美国家,20世纪70年代法国就已将伪随机码和脉冲复合调制引信应用于“海响尾蛇”导弹;我国近些年来,也对该类信号进行了研究和分析[1114]-。其中文献[11,12]对不同体制的伪码调制脉冲串信号及应用进行了介绍,文献[13,14]对抗噪声性能进行了分析,而在参数提取方面,文献[7,8]中方法可被用来估计伪随机二相编码脉冲串信号的参数,然而对于本文所提的经过脉位调制的脉冲串信号,现阶段的方法还不能够很好地解决其参数提取问题。本文受文献[5,6]方法启发,利用伪码调制脉冲串广义周期性特点,提出实现多分量信号分离和参数估计的方法,较好地解决了对各种伪码调制脉冲串信号的调制参数和伪码进行估计的问题。
2 单通道多分量伪码调制脉冲串信号
单通道多分量伪码调制脉冲串信号表示为

式中sT为采样周期,M为伪码调制脉冲串分量个数,对于第i个分量 si[n],iA为幅度,0为载频,0为初始相位,为相位函数,v[ n]表示高斯白噪声,Ui[ n]表示伪码序列。根据文献[13]定义,为子脉冲宽度,为子脉冲重复周期,为高频脉冲周期 TPi= PiTmi,iP为伪码码元数,也为一个 i周期内的子脉冲个数, Xip={0,1,…, Pi-1}对应脉位位置,Cip={+ 1,-1 }同 Xip均由 Pi位的伪随机码序列决定,ipX 的各个值在一个iPT 周期内均出现一次。对第i个分量,按文献[13]定义,当其参数ipC 和ipX 取特定值时,可以表示为相应的脉冲伪码体制信号:(1)Cip={+ 1,- 1}且 Xip≡ 0时,为PRBC脉冲串信号;(2)Cip≡ 1且 Xip={0,1,…, Pi-1}时,为PPM脉冲串信号;(3)Cip={+ 1,- 1}且 Xip={0,1,…,Pi-1}时,为PRBC-PPM脉冲串信号。
3 参数及伪码序列估计
在详细介绍本文方法各步骤之前,需先进行说明的是:利用本文提出的方法,每次估计出的参数和伪码序列对应于式(1)[]x n中平均能量最大的分量,从 []x n中减去对该分量的重构能够完成分离。假设对于式(1)所示模型有,由于分量能量正比于则信号分离及参数提取是按照 1i M= ~ 的顺序进行的。在 b- 1(b = 1,…, M)次分离之后,有 b- 1个分量从多分量信号中被减去,剩余信号为

3.1 伪码调制脉冲串信号的广义周期
对于 x[ n]中的第i个分量 si[ n],其中 Ui[ n]是以NPi为周期的周期函数,则对于正整数l有
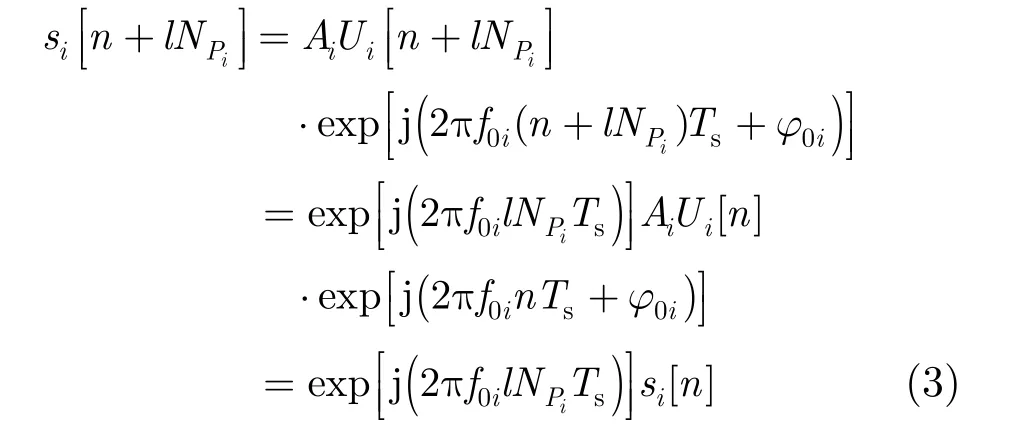
式(3)说明各分量是以iPN 为广义周期的信号,其各个周期内值按周期iPN 存在比例关系,定义i分量相差l周期的比例因子为即在式(2)中共有 M -b+1个分量,为求解分量广义周期,按文献[5,6,15]方法求得的奇异值比(SVR)谱中存在与各分量相对应位置为N = NPi(i = b, b + 1,…,M)的多个峰值,各峰值同分量能量成正比。对于 x(b-1)[n]中分量有则与谱中最高峰值所对应的 N = NPb。
3.2 周期积累
当通过构建奇异值比谱的方法得到 sb[ n]的广义周期bPN 后,可通过周期积累减小噪声和其他周期不为 NPb的分量 si[ n]( i = b + 1,… ,M)对分量 sb[ n]的影响。假设取L个周期进行周期积累,则积累后的信号为
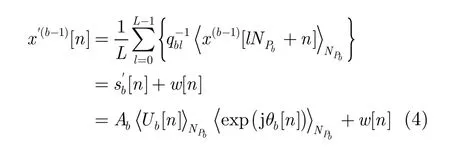
3.3 载频估计
对式(4)进行平方处理,得到式(5):

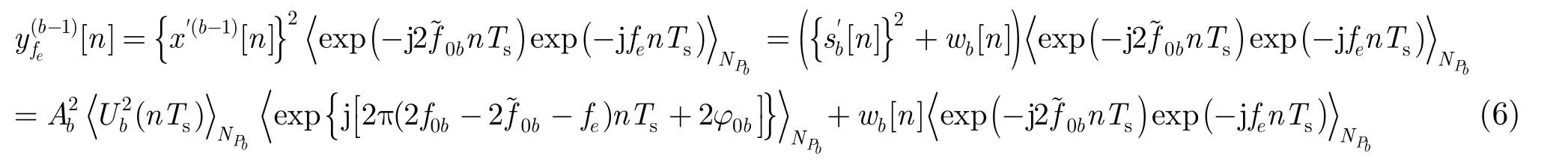


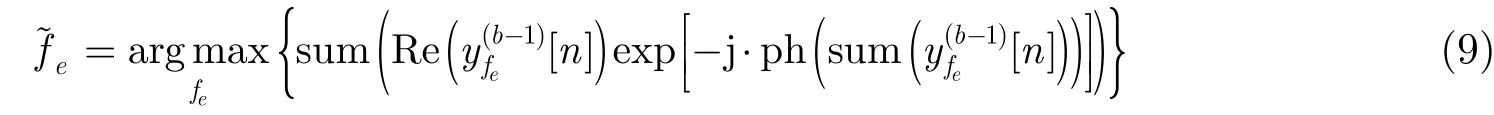
从而得到对载频的精确估计:

3.4 对脉位调制波形进行估计

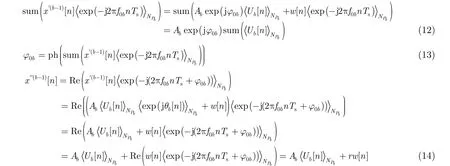


3.5 对伪码序列的估计

3.6 幅度及初始相位估计

因此,可得幅度及初始相位如式(19),式(20)所示,即估计出各参数,则能够重构该分量如式(21)所示。

重构后可将该分量从 x(b-1)[n]中减去得到新,重复第 3节步骤就能完成对剩余分量的重构。当某次分解之后信号剩余能量小于某个阈值时,认为只剩下噪声,可以停止分解。该阈值的确定同文献[5,6]中第3节方法类似,利用自相关矩阵特征值分解法[16]来估计信噪比并得到噪声能量SPv,并得到阈值。
4 仿真与分析
本文对信噪比为 5 dB的单通道三分量伪码调制脉冲串信号进行分离,采样频率 Fs= 204.8 MHz ,各分量对应的参数如表1所示。以上述参数得到的各 Ui( t)波形如图1所示。混合信号示意图如图2所示。首先,按照文献[5,6,16]估计信噪比为SNR= 4.911 dB,并计算得到SPv = 0.0,2当33 0.1δ= 时,阈值
仿真流程为:(1)奇异值比谱如图3,周期估计为 NP1= 2450点;(2)周期积累和平方处理后得时域及频域表示如图4~图6所示,从频谱找到载频粗略估计值取 2n0f=0 0及 Δf = 2 kHz ,得搜索区间为[-4 MHz,4 MHz],搜索示意图如图7所示得到从而得精确载频去载频处理得到如图8所示波形;(6)整形后脉冲序列如图 9所示,设定延迟因子为3,得到进一步处理后的波形如图 10所示;(7)从图 10波形可以得到表2中列出各段数据的 1± 值则得到1pC 的值,并确定 X1p值;(8)估计出幅度 A1= 0.5985及初始相位φ01=2 .4;16(59)重构信号并同源信号对比如图11,图12所示。将重构波形从混合信号中减去再重复各步骤直到停止分解,参数估计结果列于表 3。可以看出很好地估计出了各参数,且恢复分量同原分量波形相似度都达到了99%以上。波形相似度计算公式为

式中ρ为两个信号 ()y t和 ()s t的相似度, []E·表示求期望值。第 1,第 2次分解完成之后,剩余信号平均能量分别为0.0443和0.0334均大于阈值,第3次分解之后剩余信号平均能量 0.0255小于阈值0.0305,停止分解。

表1 各分量信号参数

图1 各分量伪随机调制脉冲序列示意图
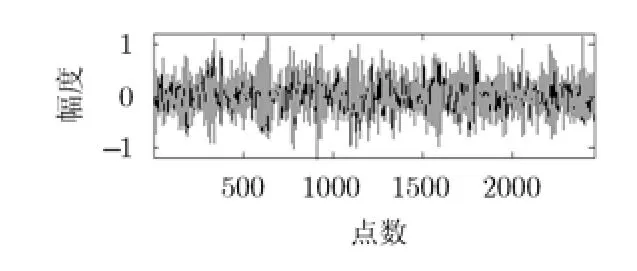
图2 混合信号示意图

图3 奇异值比示意图

图4 周期积累后信号

图5 平方处理后信号

图6 载频粗略值估计示意图

图7 载频精确值搜索示意图

图8 去载频处理后波形
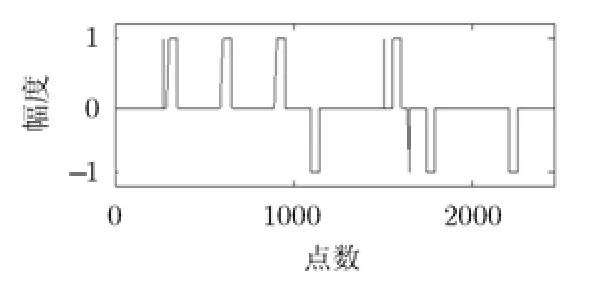
图9 整形后脉冲序列图

图10 进一步处理后的脉冲序列

图11 重构信号

图12 源信号

表2 pC1及pX1估计示意表
为说明本文方法有效性,图13~图15给出不同信噪比条件下本文方法和模糊函数法[7]、谱相关方法[8]对不同参数的估计精度,从图中可以看出本文方法对各参数估计均达到较高精度。需要指出的是,谱相关方法和模糊函数法只能有效解决PRBC脉冲串信号的参数估计问题,然而却无法较好地分析本文所提到的经过脉位调制的脉冲串信号,而本文方法优势在于能够被用来有效解决经脉位调制的脉冲串信号的参数估计问题。
图 16给出不同信噪比下各次分解后剩余能量及阈值相对于初始总能量比值曲线,阈值曲线随着输入信噪比的变化而变。当信噪比较小时,由于噪声能量占观测混合信号能量的比重较大,使得各次分解后的能量曲线相距较近,此时信噪比估计误差对阈值的影响较大,即使δ取不同值,都容易出现阈值曲线不在最后两次分解后剩余能量曲线的中间,分解不完全或分解不停止的情况。然而由于阈值曲线随δ的变小而下移,那么为了在信噪比较低时保证分解的成功,通常取较大的δ值,那么就容易无法分解出混合信号中能量较小的分量。而当信噪比不至于过低时,由于噪声能量所占比重减小,使得各次分解后剩余能量的曲线相距较远,那么此时就不容易出现分解不完全或不停止的情况,且δ值的选取可以较小,容易分解出混合信号中能量较小的分量。所以,对于绝大多数非极端情况下(信噪比不至于过低,各分量信号能量不至于太小)的混合信号,用本文方法进行信号分离和参数估计,能够保证分解的成功和参数估计的较高精确度

表3 各恢复分量参数

图14 载频估计精度
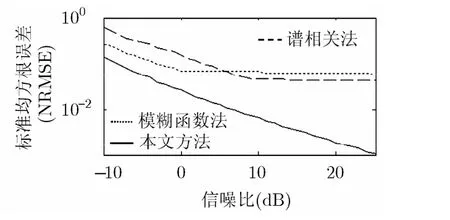
图15 初始相位估计精度
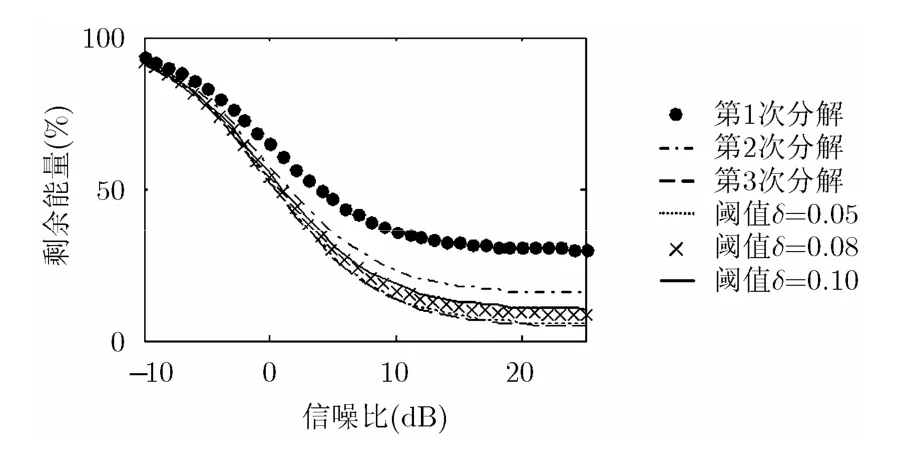
图16 不同信噪比各步分解后能量同阈值的比较
5 结束语
本文提出一种噪声条件下多分量伪码调制脉冲串信号的分离和参数估计方法,在利用奇异值比谱估计出分量信号的广义周期后,通过周期积累减小噪声及干扰影响,利用平方处理和搜索算法精确估计载频并完成脉冲串位置估计,并通过内积计算来估计幅度和初始相位。此外,本文还利用自相关矩阵特征值分解法估计出混合信号的信噪比以确定停止分解的阈值,保证准确分解出各个分量。仿真中,通过分析不同信噪比条件下的参数估计标准均方差曲线及阈值曲线,说明本文方法对于绝大多数非极端条件的单通道多分量伪随机码调制脉冲串信号分离和参数提取问题,可以达到良好的效果,且对各参数的估计能达到较高的精度。在今后进一步的研究中,应考虑减少噪声和干扰对参数估计精度的影响,实现更低信噪比条件下的参数高精度估计。
[1] 黄光明,赵惠昌,熊刚,等. 基于分数阶傅里叶变换的无线电引信信号的侦察[J]. 电子与信息学报,2005,27(3):431-433.
Huang Guang-ming,Zhao Hui-chang,Xiong Gang,et al.. Radio fuze signal reconnaissance based on fractional fourier transform[J]. Journal of Electronics & Information Technology,2005,27(3):431-433.
[2] 朱健东,赵拥军,唐江. 线性调频连续波信号的周期分数阶Fourier变换检测与估计[J]. 电子与信息学报,2013,35(8):1827-1833.
Zhu Jian-dong,Zhao Yong-jun,and Tang Jiang. Periodic FRFT based detection and estimation for LFMCW signal[J]. Journal of Electronics & Information Technology,2013,35(8):1827-1833.
[3] 张淑宁,赵惠昌,熊刚,等. 基于粒子滤波的单通道正弦调频混合信号分离与参数估计[J]. 物理学报,2014,63(15):158401.
Zhang Shu-ning,Zhao Hui-chang,Xiong Gang,et al.. Separation and parameter estimation of single channel sinusoidal frequency modulated signal mixture sources based on particle filtering[J]. Acta Physica Sinica,2014,63(15):158401.
[4] 朱航,张淑宁,赵惠昌. 基于改进自适应分解法的单通道雷达引信混合信号分离[J]. 物理学报,2014,63(5):058401.
Zhu Hang,Zhang Shu-ning,and Zhao Hui-chang. Singlechannel source separation of radar fuze mixed signal using advanced adaptive decomposition[J]. Acta Physica Sinica,2014,63(5):058401.
[5] 朱航,张淑宁,赵惠昌. 单通道多分量伪码复合线性调频信号分离及参数提取[J]. 兵工学报,2014,35(9):1363-1374.
Zhu Hang,Zhang Shu-ning,and Zhao Hui-chang. Single channel source separation and parameters estimation of multi-component PRBC-LFM signal [J]. Acta Armamentarii,2014,35(9):1363-1374.
[6] 朱航,张淑宁,赵惠昌. 基于广义周期性的单通道多分量正弦调频信号分离和参数估计[J]. 电子与信息学报,2014,36(10):2438-2444.
Zhu Hang,Zhang Shu-ning,and Zhao Hui-chang. Single channel source separation and parameters estimation of multi-component sinusoid frequency modulation signal based on generalized periodic[J]. Journal of Electronics & Information Technology,2014,36(10):2438-2444.
[7] 张淑宁,朱航,赵惠昌,等. 基于周期模糊函数的伪码调相与正弦调频复合引信信号参数提取技术[J]. 兵工学报,2014,35(5):627-633.
Zhang Shu-ning,Zhu Hang,Zhao Hui-chang,et al.. Parameter extraction technique based on periodic ambiguity for PRCPM-SFM compound fuze signal[J]. Acta Armamentarii,2014,35(5):627-633.
[8] 熊刚,赵惠昌,王李军. 伪码-载波调频侦查信号识别的谱相关方法(Ⅱ)—伪码-载波调频信号的调制识别和参数估计[J].电子与信息学报,2005,27(7):1087-1092.
Xiong Gang,Zhao Hui-chang,and Wang Li-jun. Reconnaissance signal recognition of PN code-carrier FM based on spectral correlation method(Ⅱ)—The modulation recognition and parameter estimation of PN code-carrier FM[J]. Journal of Electronics & Information Technology,2005,27(7):1087-1092.
[9] 陆锦辉,是湘全,丁庆海. 随机脉位脉冲串雷达信号分析[J].南京理工大学学报,1995,19(5):445-448.
Lu Jin-hui,Shi Xiang-quan,and Ding Qing-hai. The analysis of randomly staggered pulse sequence radar signal[J]. Journal of Nanjing University of Science and Technology,1995,19(5):445-448.
[10] 陆锦辉,是湘全,丁庆海,等. 随机脉位调制脉冲序列的平均模糊函数[J]. 现代雷达,1995,17(2):41-46.
Lu Jin-hui,Shi Xiang-quan,Ding Qing-hai,et al.. Average ambiguity function for a randomly staggered pulse sequence[J]. Modern Radar,1995,17(2):41-46.
[11] 刘己斌,赵惠昌. PPM伪随机码及其应用[J]. 现代雷达,2004,26(2):23-26.
Liu Ji-bin and Zhao Hui-chang. PPM pseudo-random code and its applications[J]. Modern Radar,2004,26(2):23-26.
[12] 邓建平,赵惠昌,周新刚,等. 伪随机脉位调制与单极性伪码调相复合体制引信[J]. 宇航学报,2007,28(2):398-403.
Deng Jian-ping,Zhao Hui-chang,Zhou Xin-gang,et al.. Pseudo random pulse position modulation and unipolar pseudo random coded phase-modulation combined fuze[J]. Journal of Astronautics,2007,28(2):398-403.
[13] 熊刚,杨小牛,赵惠昌,等. 伪随机码调制脉冲串引信及其抗噪性能分析[J]. 弹箭与制导学报,2006,26(S2):469-472.
Xiong Gang,Yang Xiao-niu,Zhao Hui-chang,et al.. The analysis of PN code modulated by pulse train[J]. Journal of Projectiles,Rockets,Missiles and Guidence,2006,26(S2):469-472.
[14] 周新刚,赵惠昌,邓建平. 伪码调相与伪随机PPM复合引信的抗噪声性能分析[J]. 南京理工大学学报(自然科学版),2008,32(5):623-627.
Zhou Xin-gang,Zhao Hui-chang,and Deng Jian-ping. Analysis of anti-noise performance for pseudo-random code phase modulation combined with PPM fuze[J]. Journal of Nanjing University of Science and Technology (Natural Science),2008,32(5):623-627.
[15] Kanjilal P P. Fetal ECG extraction from single-channel maternal ECG using singular value decomposition[J]. IEEE Transactions on Biomedical Engineering,1997,44(1):51-59.
[16] 张金成,彭华. 一种鲁棒的基于子空间分解的盲信噪比估计方法[J]. 数据采集及处理,2011,26(5):609-614.
Zhang Jin-cheng and Peng Hua. Robust blind SNR estimation method based on subspace decompositon[J]. Journal of Data Acquisition and Processing,2011,26(5):609-614.
朱 航: 男,1987年生,博士生,研究方向为信号处理和数字仿真.
张淑宁: 女,1977年生,副研究员,硕士生导师,研究方向为非平稳信号处理、无线电侦察信号分析与处理.
赵惠昌: 男,1958年生,教授,博士生导师,研究方向为引信对抗、信号处理及数字仿真.
Single Channel Source Separation and Parameters Estimation of Multi-component Pseudo-random Code Modulated Pulse Train
Zhu Hang①②Zhang Shu-ning①Zhao Hui-chang①
①(School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)
②(Unit 73015 of PLA,Huzhou 313000,China)
For the several kinds of pseudo-random code modulated pulse trains-the Pseudo-Random Binary Code(PRBC) pulse train,including the Pulse Position Modulation (PPM) pulse train,the Pseudo-Random Binary Code and Pulse Position Modulation (PRBC-PPM) pulse train,in order to solve the problem of single channel source separation and parameters estimation of multi-component signal,an estimation method of carrier frequency and pseudo-random code based on Singular Value Ratio (SVR) spectrum and cycle accumulation is proposed. The generalized period can be estimated through SVR spectrum firstly,after that the interference of the noise can be reduced by cycle accumulating,Fast Fourier Transformation (FFT) is used to analyze the squared signal,and the exact value of carrier frequency and the pulse position can be obtain by measuring the sum value of the real part of the signal which removed carrier frequency. At last,the amplitude and the initial phase can be determined by calculating the inner product. The simulation results prove that the proposed method is effective in different SNRs.
Signal processing;Multi-component signal;Pseudo-random code modulated pulse train signal;Parameters estimation;Source separation;Generalized period
TN971.1
A
1009-5896(2015)07-1702-08
10.11999/JEIT141317
2014-10-15收到,2015-02-04改回,2015-05-08网络优先出版
国家自然科学基金(61301216)和省部级基金资助课题
*通信作者:张淑宁 a353eoenjust@163.com
