基于模糊PID主动控制的仿真及应用

罗庆，黄民翔，郭雨涵

（浙江大学电气工程学院，浙江杭州310027）

基于模糊PID主动控制的仿真及应用

罗庆，黄民翔，郭雨涵

（浙江大学电气工程学院，浙江杭州310027）

针对电气化铁路中的接触网-受电弓系统，提出模糊主动控制、PID主动控制，并结合两者的优点建立模糊PID主动控制；根据受电弓的特点，建立受电弓三元质量块模型，并推导出受电弓的动力学方程、状态空间方程和传递函数；利用Simulink仿真手段，对被动控制、模糊主动控制、PID主动控制、模糊PID主动控制的弓网系统动态性能进行仿真研究。仿真结果表明：模糊PID主动控制策略可以最大程度的降低弓网系统接触压力的波动，提高弓网系统的受流质量。

受电弓；集中质量块；仿真分析；主动控制

高速电气化铁路中，良好的弓网关系是铁路稳定、可靠运营的基本保障。受电弓与接触网良好的接触特性是弓网关系中接触悬挂向列车传递可靠电能的先决条件。然而，随着列车运行速度的提高，受电弓与接触网之间的相互作用暴露出很多问题，如接触线振动加大、电弧烧蚀、弓网冲击等，这些状况大大降低了弓网品质［1］。

目前就弓网系统耦合研究而言，日本、德国、法国等国家的弓网系统性能达到比较理想的匹配效果，已基本能够适应350 km/h及以上的运行速度。

在国内，很多学者对如何提高弓网系统的接触性能以及改善弓网系统动态受流质量的方法进行深入的研究，通过研究弓网系统的运动情况来找出影响弓网系统受流质量的主要因素，并作为提高弓网系统受流质量的突破口。但国内在这方面的主要研究还局限于被动式的弓网系统受流方式，并且绝大多数的方法都需要对接触网进行大规模的改造才可以达到比较理想的弓网系统受流质量［2］。由于我国电气化铁路辽阔，改造接触网将耗费大量的物力和财力，这使得研究人员提出的改善弓网系统受流质量的措施和方法受到经济条件和物理条件等诸多因素的限制。

在弓网系统中，弓网接触压力是评判弓网系统受流质量的主要标准之一。然而当受电弓在多频激励耦合作用下工作时，想要得到一个为恒定值的接触力是非常困难的。通常有3条途径解决这类问题：

1）使电力机车的轨道更加平顺，则在运行过程中可以使受电弓受到的扰动减小；

2）增大接触线和受电弓之间接触力；

3）增大接触线的张力或增大接触网的刚度［3］。对既有线路，要增加接触网的刚度，提高接触线的张力或提高轨道的平顺性都比较困难。

对此，本文在不改变接触悬挂本身设计结构的前提条件下，通过对受电弓进行主动控制，使受电弓性能得到优化，并且为改善弓网关系提供一条有效的途径。

1 弓网系统建模

1.1 接触网时变刚度模型

我们以简单链形悬挂接触网模型来介绍接触网的时变刚度模型。在文献［4］中，作者把接触网看成一个时变刚度系统，并且把接触网的模型简化为下式：

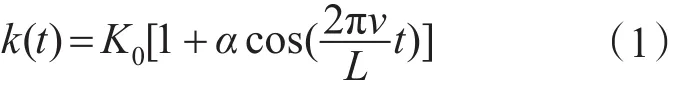
式中：K0为接触网的平均刚度；v为列车运行的速度；L为接触网的跨距；k(t)为接触网的实时刚度；α为接触网刚度差异系数。

在接触网一个跨距内，各个位置的刚度都是不同的，当电力机车在运行中，经过一个跨距时，经过该跨距内的不同位置，所得到的k(t)值是不同的。

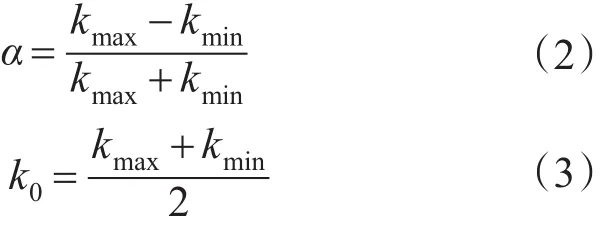
式中：kmax，kmin分别为接触网一个跨距内的最大刚度、最小刚度。

接触网的刚度差异系数是指在一跨距内，接触网的最大静态刚度与最小静态刚度的和与最大静态刚度与最小静态刚度的差的比值，刚度差异系数也是作为评价接触网-受电弓系统中受流质量的一个重要指标之一。静态刚度k(x0)是指在跨距内的某点(x=x0)处垂向作用一个单位抬升力所引起的位移y(x0)的倒数，其计算式可表示成下式：

1.2 受电弓集中质量块模型

目前，在对受电弓进行建模分析时，一般采用受电弓集中质量块模型。受电弓集中质量块模型是利用动能等效原理将受电弓分为几个由集中质量块模型组成的模型，该模型主要用于分析受电弓的动力学特性［5］。

在受电弓集中质量块模型中，根据集中质量块的数量可以将模型分为一元质量块模型、二元质量块模型、三元质量块模型及四元质量块模型等多元模型。集中质量块越多，则所建立的模型更能准确地描述出受电弓的实际动力学特性［6-7］。图1列出了常见的模型。

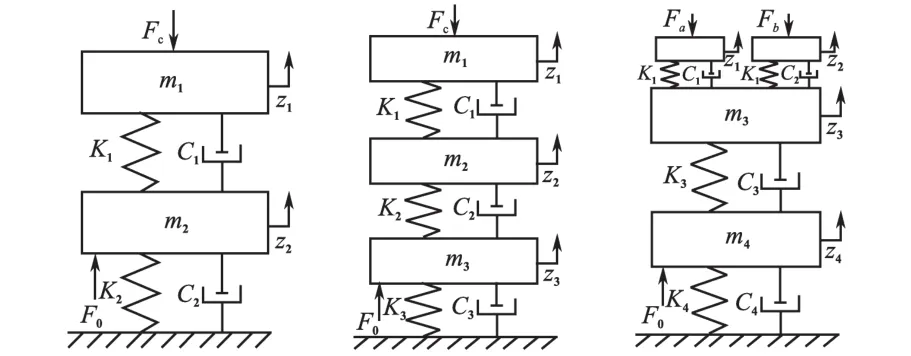
图1 受电弓二元、三元、四元质量块模型Fig.1 The mass model of pantograph

论文采用三元质量块模型，对模型中的3个集中质量块进行受力分析，得到受电弓的动力学方程：

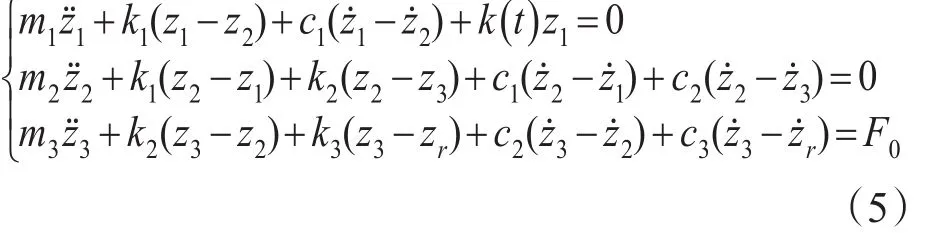
式中：m1为受电弓的弓头质量；m2为受电弓上框架的质量；m3为受电弓下框架的质量；k1为弓头与上框架之间的刚度系数；k2为上、下框架间的刚度系数；k3为车体与下框架之间的刚度系数；k(t)为接触线与受电弓之间的等效刚度；c1为受电弓弓头和上框架之间的阻尼系数；c2为受电弓上、下框架之间的阻尼系数；c3为车体与受电弓下框架之间的阻尼系数；z1为受电弓弓头的位移，取向上为正方向；z2为受电弓上框架的位移，取向上为正方向；z3为受电弓下框架的位移，取向上为正方向［8-9］。

完成模型的建立并通过受力分析得到受电弓动力学方程，并将其转换成状态空间的形式［10］：

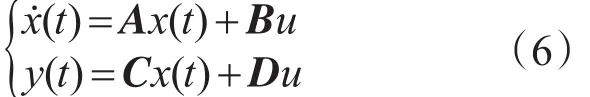
其中

1.3 传递函数

论文以DSA250型受电弓为例。DSA250型受电弓由德国STEMMANN公司设计，北京赛德公司在2001年从德国STEMMANN公司技术引进DSA250型受电弓，并于2002年完成国产化的工作。根据文献［11］得到DSA250型受电弓三元质量块模型的参数，见表1。

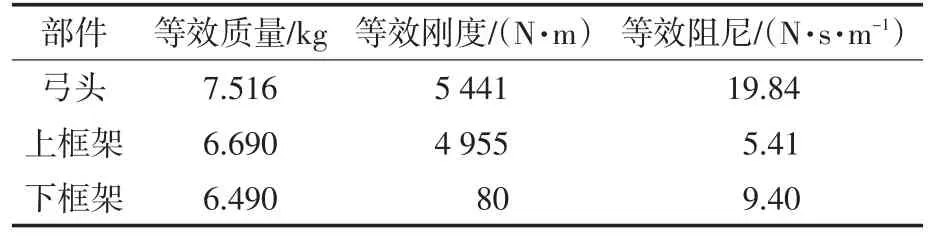
表1 DSA250型受电弓三元质量块模型参数Tab.1 Model parameters of DSA250 pantograph

由表1中的数据及受电弓三元质量块模型的状态空间方程，编程求得DSA250型受电弓的传递函数为

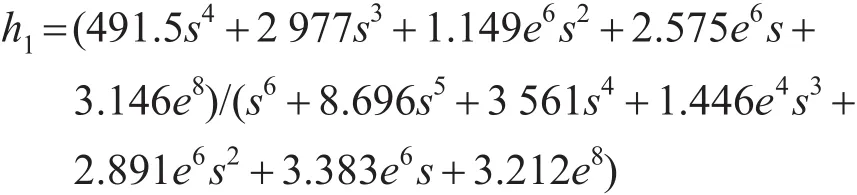
2 主动控制及效果分析

2.1 模糊主动控制

采用Matlab中的模糊工具箱，建立单输入单输出的模糊推理系统［12］。输入为实际弓网接触压力与理想弓网接触压力的误差值，即

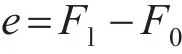
式中：e为误差；Fl为弓网接触压力的实际值；F0为弓网接触压力的理想值，本文中设定F0=100 N。

模糊推理系统的输出为弓网接触压力；输入变量隶属函数采用Trimf基本函数拼接而成，输出变量的隶属函数采用5个定值，分别为50 N，75 N，100 N，125 N，150 N。图2为模糊主动控制的简略框图。

图2 受电弓模糊主动控制简略框图Fig.2 The block diagram of pantograph′s fuzzy active control

利用建立的模糊推理系统，在Simulink中创建受电弓仿真模型。输入量为理想值F0=100 N，返回值为每次仿真得到的实际弓网接触压力，两者的误差作为模糊推理系统的输入，经过模糊规则后得到输出结果。DSA250型受电弓在模糊主动控制下的弓网接触压力的波形如图3所示。

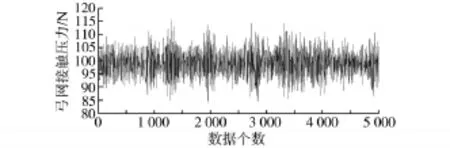
图3 受电弓模糊主动控制下的弓网接触压力波形Fig.3 Contact pressure waveform of the pantograph′s fuzzy active control

从图3可以看出，DSA250型受电弓在模糊主动控制下，能够在80～120 N之间波动，仿真数据指标为：平均值99.752 58 N，最大值115.521 N，最小值84.114 87 N，标准差4.552 087 N。

2.2 PID主动控制

PID控制器是由3部分组成的，分别为比例、积分、微分，其输入e(t)与输出u(t)的关系式为

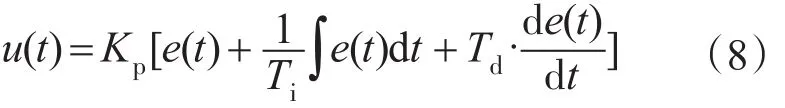
PID控制器具有稳定性好、调整方便、结构简单，并且易于掌握。常规的一些控制方法对于一些构造复杂，模型不够精确或者一些参数比较模糊的系统无法进行良好的控制，但运用PID控制技术较为方便。PID系统就是根据系统的误差，利用比例、积分、微分3个模块的配合对系统进行控制。图4为受电弓在PID主动控制下的框图模型。

图4 受电弓PID主动控制简略框图Fig.4 The diagram of pantograph PID active control

通过试凑法，PID控制器中当比例系数Kp为0.6，积分系数Ki为2，微分系数Kd为0时，可以使仿真所得的弓网接触压力较为稳定，波动程度也较小，控制稳定。

从图5可以看出，DSA250型受电弓在PID主动控制下，能够在80～120 N之间波动，仿真数据指标为：平均值100.097 8 N，最大值117.529 1 N，最小值83.368 89 N，标准差4.685 284 N。

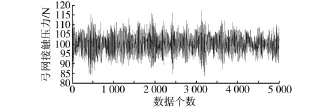
图5 受电弓PID主动控制下弓网接触压力Fig.5 Contact pressure waveform of the pantograph PID active control

2.3 模糊PID主动控制

模糊主动控制的优势在于可以在大偏差范围内利用模糊推理的方法得到合适的结果，减小输出量的偏差，而PID控制对于一些输出量在小偏差范围内的系统具有较好的控制效果。结合两种主动控制的优势，建立模糊PID主动控制，共同作用于受电弓系统，并且当仿真输出的弓网接触压力与理想的弓网接触压力的误差值较大时，系统启动模糊主动控制，误差值较小时，系统启动PID主动控制，该策略同时拥有模糊主动控制和PID主动控制的优点，可以进一步降低弓网接触压力的波动程度，提高弓网系统的受流质量。

图6中，系统在进行主动控制之前加入了误差判断模块，该模块能设定一个阀值。仿真过程中，误差首先输入误差模块并与设定的阀值进行比较，如果误差高于阀值，启动模糊主动控制；如果误差低于阀值，则启动PID主动控制。

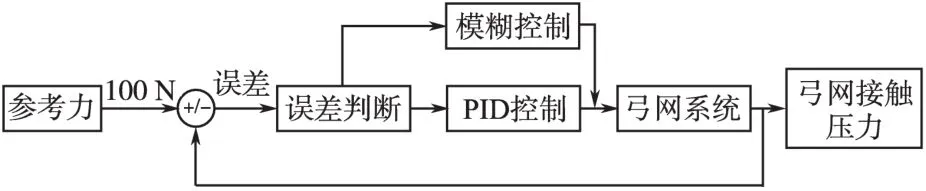
图6 受电弓模糊PID主动控制简略框图Fig.6 The diagram of pantograph fuzzy PID active control

为研究受电弓主动控制达到的效果，论文同时建立受电弓在被动控制下的模型并进行仿真研究。

从图7的仿真波形中可以分析，DSA250型受电弓在主动控制下弓网接触压力的波动范围明显比在被动控制下弓网接触压力的波动范围小得多。仿真数据如表2所示。

图7 受电弓模糊PID主动控制和被动控制下的波形Fig.7 Contact pressure waveforms of the pantograph fuzzy PID active control and the passive control

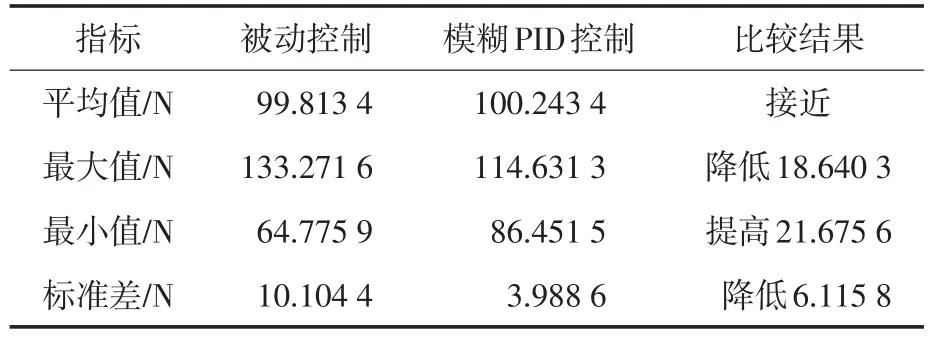
表2 受电弓模糊PID主动控制及被动控制的数据Tab.2 Contact pressure data of the pantograph fuzzy PID active control and the passive control

从表3可以分析得到，模糊PID主动控制效果最好，被动控制效果最差，模糊主动控制和PID主动控制效果接近，且都明显优于被动控制。模糊PID主动控制结合了模糊主动控制和PID主动控制的优点，可以提高弓网接触压力的最小值，降低弓网接触压力的最大值，改善弓网接触压力的波动程度，仿真结果符合理论预期结果。

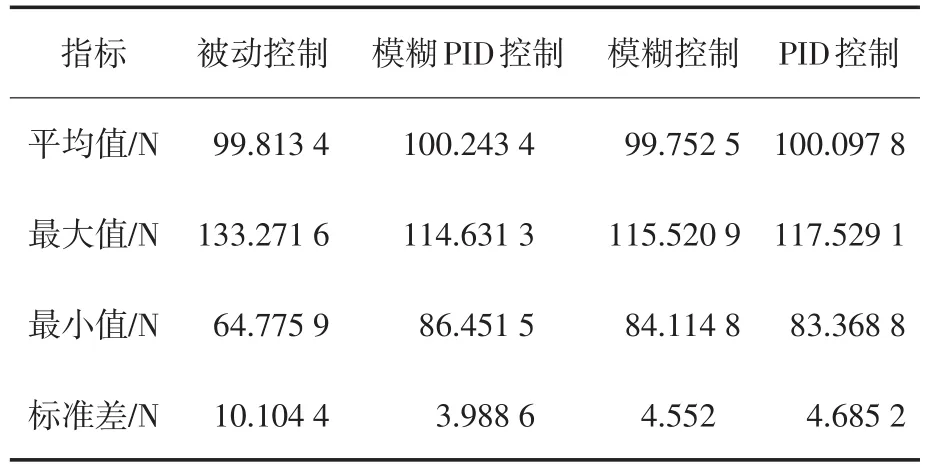
表3 受电弓在4种控制下的弓网接触压力数据Tab.3 Contact pressure data of the pantograph active control and the passive control

3 结论

本文建立了受电弓三元质量块模型，通过建模计算，得到了DSA250型受电弓的传递函数。同时研究了模糊主动控制和PID主动控制的特点，建立了模糊PID主动控制模型。利用仿真手段对受电弓主动控制和被动控制进行分析。可得如下结论：受电弓在模糊PID主动控制下能最大程度地降低弓网接触力的波动幅度，减少弓网离线率，提高弓网受流质量。

［1］WU T X，Brennan M J.Active Vibration Control of a Railway Pantograph［J］.Journal of Rail and Rapid Transit，1997，211（2）：117-130.

［2］吴学杰，张卫华.受电弓/接触网半实物半虚拟混合模拟系统的研究［J］.铁道学报，2002，24（l）：14-18.

［3］郭京波，杨绍普，高国生.变刚度弓网系统主动控制研究［J］.振动与冲击，2005，24（2）：9-13.

［4］梅桂明，张卫华.受电弓/接触网系统动力学模型及特性［J］.交通运输工程学报，2002，2（1）：20-25．

［5］Doherty R，Mullane A，Nolan G，et al.An Assessment of the Impact of Wind Generation on System Frequency Control［J］.IEEE Transactions on Power Systems，2010，25（1）：452-460.

［6］Conroy J F，Watson R.Frequency Response Capability of Full Converter Wind Turbine Generators in Comparison to Conven⁃tional Generation［J］.IEEE Transactions on Power Electron⁃ics，2008，23（2）：649-656.

［7］杨向真，苏建徽，丁明，等.微电网孤岛运行时的频率控制策略［J］.电网技术，2010，34（1）：164-168.

［8］吕志鹏，盛万兴，钟庆昌，等.虚拟同步发电机及其在微电网中的应用［J］.中国电机工程学报，2014，34（16）：2592-2601.

［9］谢萍，刘永强.直驱式永磁同步风力发电系统的整合模型与仿真［J］.可再生能源，2011，29（3）：13-16．

［10］李军军，吴政球.风电参与1次调频的小扰动稳定性分析［J］.中国电机工程学报，2011，31（13）：1-9.

［11］程航，曹五顺，周明星.不对称电网电压条件下直驱永磁风力发电机组并网逆变器的双电流闭环控制策略的研究［J］.电力系统保护和控制，2012，40（7）：66-72．

［12］杨晓萍，郭鑫.直驱式永磁风力发电机组并网控制［J］.电力系统及其自动化学报，2011，23（6）：121-126.

［13］Yun Weili，Ching⁃Nan Kao.An Accurate Power Control Strat⁃egy for Power⁃electronics⁃interfaced Distributed Generation Units Operating in a Low⁃voltage Multibus Microgrid［J］. IEEE Transactions on Power Electronics，2009，24（12）：2977-2987.

Simulation and Application Based on Fuzzy PID Active Control

LUO Qing，HUANG Min⁃xiang，GUO Yu⁃han
（College of Electrical Engineering，Zhejiang University，Hangzhou 310027，Zhejiang，China）

For the pantograph⁃catenary system of the electrified railway，the fuzzy active control model，proportional integral differential（PID）active control model were discussed，and combined the advantages of these two models，the fuzzy PID active control was established.According to the characteristics of the pantograph，established the pantograph mass model，and derived the dynamic equation，state space equation and transfer function of the pantograph.Simulation study of dynamic performance of the pantograph⁃catenary system under the passive control，fuzzy active control，PID active control and fuzzy PID active control are made with software simulink.The research results show that the dynamic performance and quality of current collection of the pantograph⁃catenary system can be improved the most obviously with fuzzy PID control.

pantograph；mass model；simulation；active control

U264.3

B

2015-01-06

修改稿日期：2015-04-02

罗庆（1990-），男，硕士研究生,Email：luoqing2016@126.com