基于频率约束的经验模态分解的谐波检测方法

李月英，林家泉，李宗帅

（1.天津中德职业技术学院航空航天与汽车学院，天津300350；2.中国民航大学航空自动化学院，天津300300）

基于频率约束的经验模态分解的谐波检测方法

李月英1，2，林家泉2，李宗帅2

（1.天津中德职业技术学院航空航天与汽车学院，天津300350；2.中国民航大学航空自动化学院，天津300300）

在使用经验模式分解进行谐波检测时，经常会产生模态混叠。针对这一问题，提出了一种基于频率约束的EMD算法，该方法通过对固有模态函数中零点的分布加以频率约束，重新设计其筛分准则，减小了产生模态混叠的概率。分别采用基于频率约束的EMD、传统EMD以及瞬时无功功率法（p-q法）进行了谐波检测仿真实验。结果表明，该方法能够比较好地抑制传统EMD中存在的模态混叠问题，有效检测出基波电流与特定次谐波，且在检测精度以及基波电流相位的一致性方面都优于瞬时无功功率法。该算法可以比较好地分解出电网谐波，具有良好的应用前景。

经验模态分解；谐波检测；固有模态函数；模态混叠

各种非线性负荷（如变频器、振荡器）在电力系统的应用使得电网谐波污染日益严重。谐波使电能质量下降，降低电力系统的效率，缩短用电设备的寿命，引起继电保护装置误动，给电网带来严重危害［1］。只有快速准确地检测出电网中的谐波成分，才能有效地补偿掉谐波分量，防止其危害。

在电网谐波检测的问题上，国内外专家提出了各种不同的检测算法［2-3］，如：瞬时无功功率法（p-q法）、傅里叶变换法［4-5］、小波变换法［6-7］、自适应法［8-10］等。瞬时无功功率法可以检测出基波和谐波总量，但要求电压信号对称且无畸变，还需设计低通滤波器来提取基波分量。傅里叶变换法存在频谱泄露和栅栏效应，使得检测的信号存在较大的频率误差和相位误差。一些加窗的傅里叶变换［11-12］（Hanning窗、三角窗等）虽使精度有所提高，但其频谱泄露问题仍没有得到解决。经验模式分解算法［13］（EMD）分解是一种自适应的时间—频率信号分析法，不需要对电网角度同步，且对初始的电压和电流信号也没有要求，可将基波分量、谐波分量和系统噪声分解成特定频率的固有模态函数（IMF）之和，但其分解过程易产生模态混叠，严重时使谐波检测失去意义。总体平均经验模态分解［14-15］有效地降低了模态混叠的概率，但是需要对信号多次引入白噪声。

本文提出一种基于频率约束的EMD算法，通过修改IMF的筛分条件，使得原本仅需满足震荡特性和时域对称性的固有模态函数，还需判断其是否满足频率范围的约束，有效解决EMD分解的模态混叠问题，提高了基波的检测精度。

1 产生模态混叠的原因

模态混叠是指多个频率的震荡信号存在于同一个模态中，或者同一个频率的震荡信号存在于不同的模态中。模态混叠在谐波检测中的表现为：基波信号中混有高频信号，或者高频信号中含有基波分量，这使得EMD分解在基波检测中精度降低，严重时则失去分解的意义。

传统EMD算法有2个IMF的筛分条件，条件1规定了IMF的震荡特性，条件2则约束了IMF的时域对称性。由于没有对IMF的频率范围提出约束，因此很容易产生模态混叠，如图1所示，分解得到的固有模态函数满足筛分条件，却是高低频共存于同一个IMF中。这样的IMF不具备其应有的物理意义，进而无法应用于电网的基波检测。

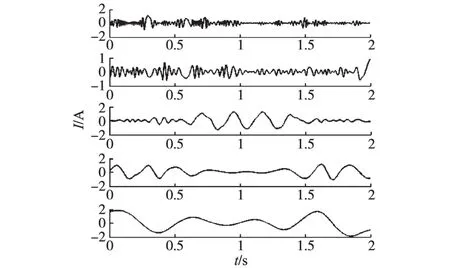
图1 EMD分解的模态混叠Fig.1 Dagram of EMD decomposition mode mixing

在实际情况中，上下包络的均值无法为零，由于最初的包络线不完全对称，故而在导致分解出的几个幅值较小的低频信号混叠在高频信号中。且如果第1次筛分的IMF存在混叠，会在后续筛分中累积放大。图1中，第1阶IMF存在明显的模态混叠，而后面几阶IMF的模态混叠也随之产生。

EMD分解存在模态混叠的问题，通过减小筛分停止准则（一般取0.2～0.3）仅能提高IMF的阶数，不能从根本上抑制模态混叠的产生，因此需要再增加筛分条件。

2 基于频率约束的EMD算法

2.1 频率约束准则

在原有振幅约束和时域对称约束的条件下，对分解出的IMF再加以频率约束，使其在分解中尽可能将信号中最高阶频率的谐波分解出来。

首先统计出该次IMF函数的零点分布的时刻记为t=[t1，t2，…，tm]，令τi=ti+1-ti，i=1，…，m-1，求出τi的均值记为E[τ]。

定义频率筛分准则δ为

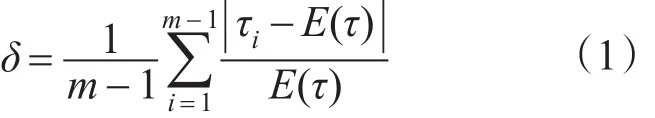
当满足δ≤ε（其中ε为选定的一个值）时筛分结束，迭代停止。

2.2 算法步骤及谐波检测过程

1）同EMD算法步骤1。

5）用原信号f(t)减去c1(t)得到1个去掉1个高频分量的新信号r1(t)：

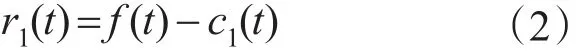
对r1(t)重复步骤1）～4）得到第2阶IMF分量c2(t)，如此反复进行，一直得到第n阶IMF分量cn(t)

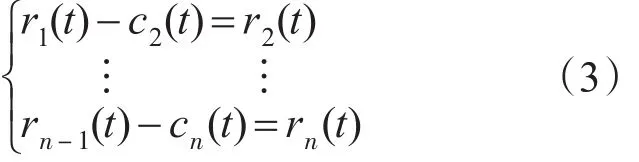
当rn(t)为一预设值或一单调函数时，筛选结束，则：

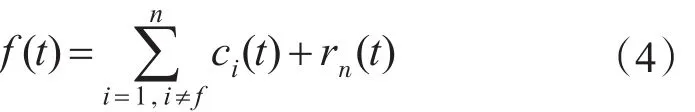
6）找出各阶IMF中，工频50 Hz附近的IMF分量cf(t)即为电网中基波分量。

7）令：X(t)=f(t)-cf(t)，重复步骤1）～6），可以检测出后一阶谐波，如此往复可以检测特定次谐波。算法流程图如图2所示。

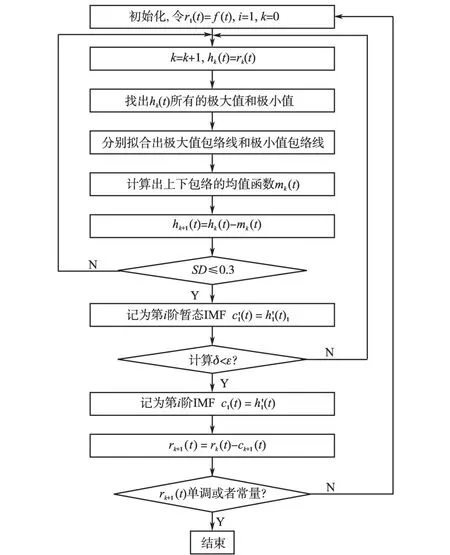
图2 算法流程图Fig.2 Algorithm flow chart

2.3 仿真数据验证

为了验证文中算法谐波检测的效果，在Matlab/Simulink环境中搭建三相整流仿真模型，图3为三相电路系统仿真模型图，仿真参数为三相模型中的电压e为100 V，f为50 Hz，阻感负载中，R=10 Ω，L=10 mH，并产生如图4所示的电流波形。

提取仿真模型中A相电流，对A相电流ia按照本文算法步骤进行分解，并选取工频50 Hz附近的IMF分量作为基波分量，且按照本文算法步骤可以求出下一阶谐波分量。

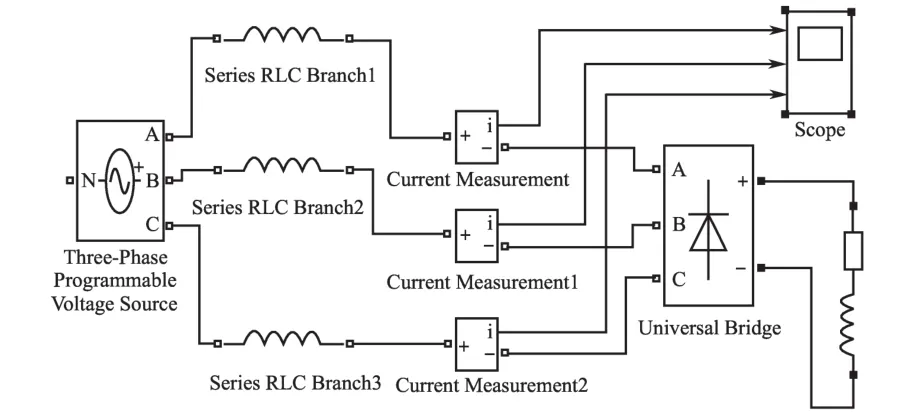
图3 三相电路系统仿真模型Fig.3 Three phase circuit system simulation model

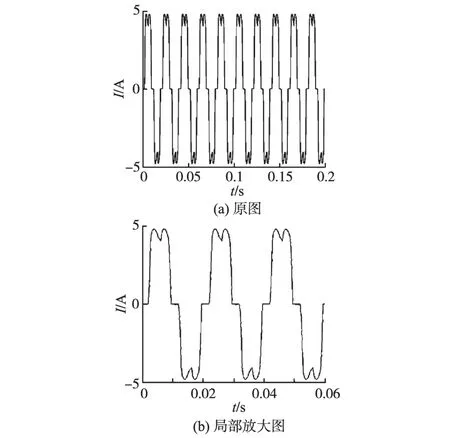
图4 A相电流仿真波形Fig.4 Current waveform of A⁃phase

文中仿真模型采用6脉波整流，故其谐波含量为6n±1次谐波，即5次谐波分量，如图5所示。

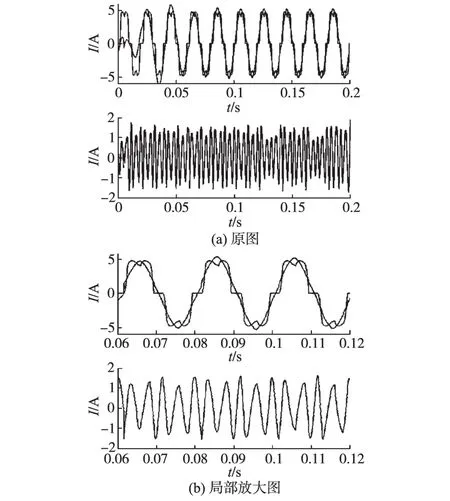
图5 A相电流与检测的基波电流和5次谐波Fig.5 Current waveforms of A⁃phase and its fundamental component and the 5th harmonic

本文算法对仿真的A相电流具有很好的跟踪特性和自适应性，在前3个周期内由于受到算法本身初值的影响与实际基波波形有较大差值外，本算法能检测出较好的基波电流。除基波电流外，本文算法能较好地检测出5次谐波电流，如图5所示，检测出的5次谐波的含量占电流总量的18.7%，与理论计算值相近，验证了该算法的有效性。

搭建如图6所示p-q法谐波检测模型，选取低通滤波器LPF的截止频率为80 Hz，对A相电流进行检测。

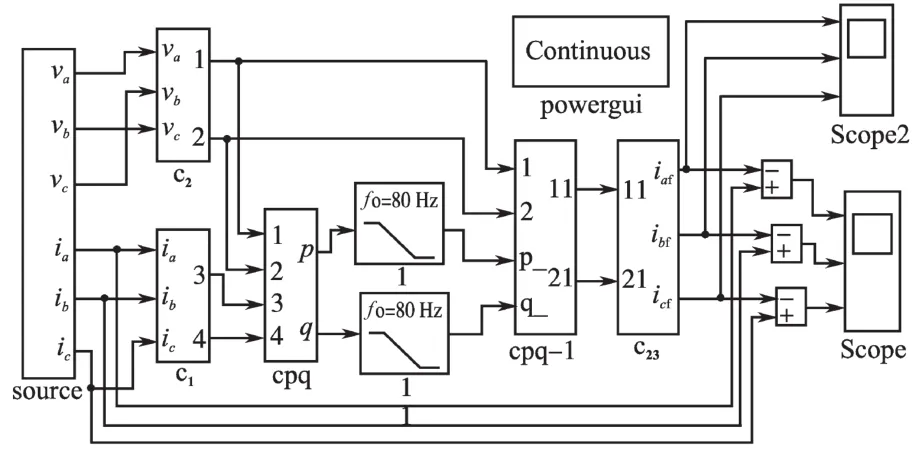
图6 p-q法谐波检测的仿真模型Fig.6 Simulation model of harmonic detection for p-q method

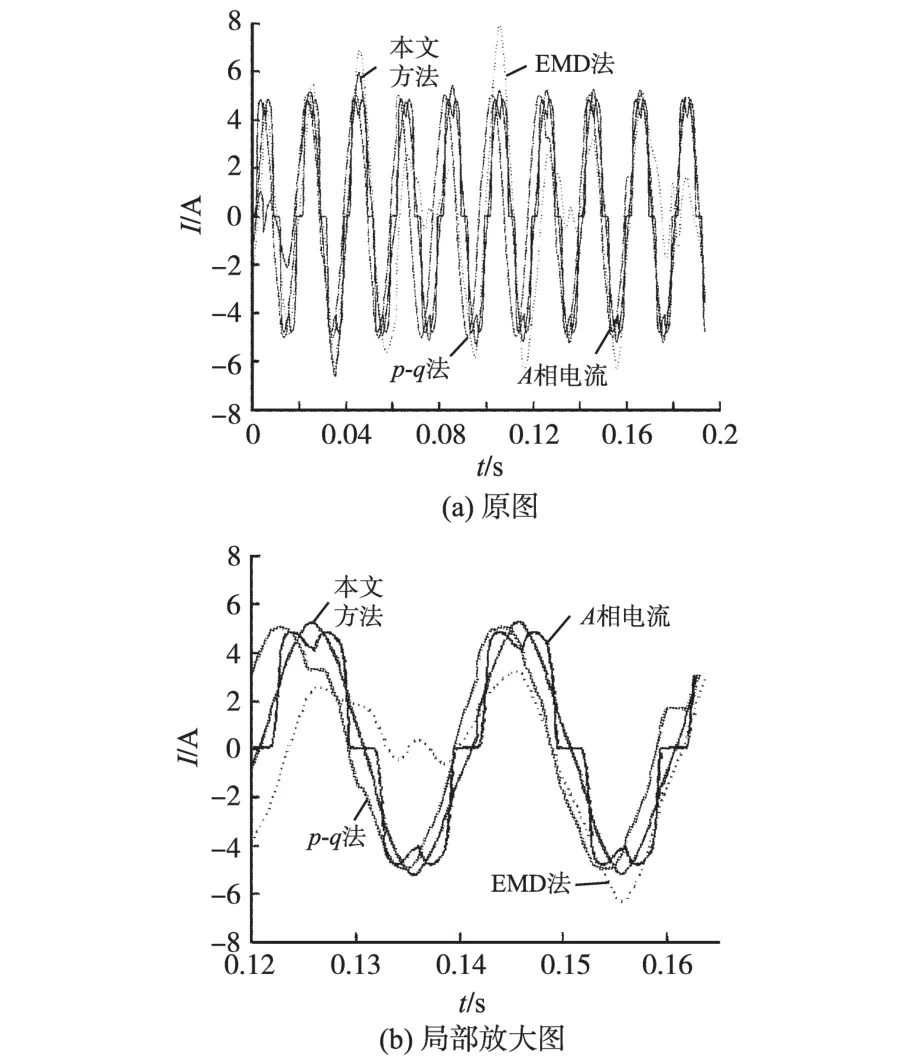
图7 新方法与p-q法、EMD法检测基波对比Fig.7 Comparison of fundamental component between p-q method，EMD and the novel method

将检测的基波电流与传统的EMD法所得结果和本文方法所得结果对比，如图7所示。传统EMD方法提取的基波受模态混叠的影响，几乎失去了基波检测的功能，p-q法能较好地检测出基波电流，且与电流波形相一致，但是存在较大的相位偏差，且p-q法的相位偏差不稳定，有一定的随机性。本文方法初始的跟踪检测特性较p-q法差，主要原因在于EMD算法受端点效应的影响，在IMF分解过程中极值的包络线在端点处误差较大造成的。本文方法具有较强的自适应性，如图7所示，经过前3个周期的调整，提取的基波电流优于p-q法，且本文方法在电流突变时具有更好的动态响应。

2.4 实测数据验证

用FLUKE435电能分析仪从某一炼钢厂电弧炉取出一段电流数据，FLUKE435所测的电流是根据IEC61000—4—7从10/12个周期无间隙谐波组电流测量值计算而得。图8为实时信号波形，采样频率为6 400 Hz，可以看出电流信号含有大量的谐波分量。

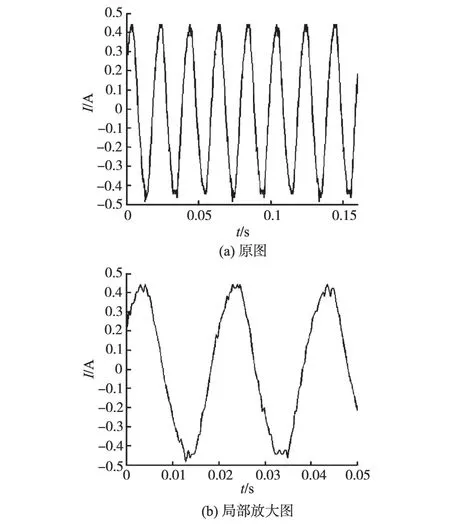
图8 实测电流波形Fig.8 Actual current waveform

如图9所示，本文算法检测的基波电流与实测电流具有很好的一致性，其幅值和相位与实测电流吻合度较好，验证了算法的有效性。利用本文算法对所取的实测电流进行经验模态分解，可以检测出基波电流和11次谐波电流如图9和图10所示。由于所取电流为12脉波整流电路的电流波形其谐波成分主要是12n±1次谐波，这也验证了本文算法对于特定谐波检测的能力。算法检测出11次谐波占电流总量的3.6%，与实测值比较吻合。

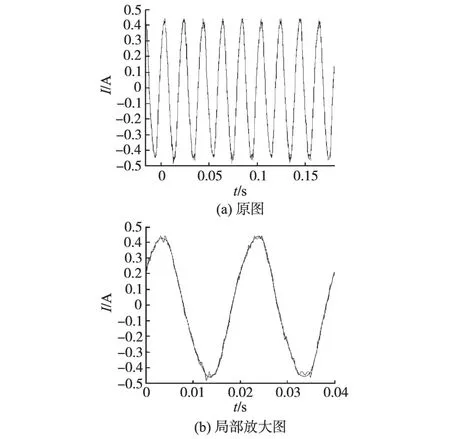
图9 检测出的基波电流与实测电流对比Fig.9 Comparison of fundamental component between the novel method and actual current

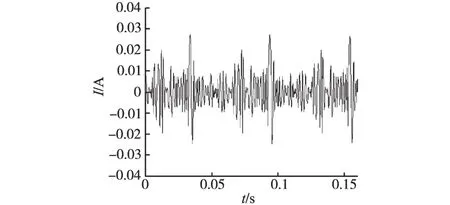
图10 11次谐波电流波形Fig.10 11thharmonic current waveform

3 结论

1）分析了传统EMD分解存在模态混叠的主要原因，仅通过减小筛分停止准则不能从根本上解决模态混叠，其模态函数筛分准则在模态分解中缺乏频率约束，且模态分解中第1阶IMF的质量尤为重要。

2）提出了一种频率约束的EMD算法，该方法减少了模态混叠的概率，提高了基波电流检测的精度。但频率约束增加了算法的复杂性，频率筛分判定准则设定过小，该算法会失效，不能检测出基波电流，频率筛分判定准则设定过大，使得模态混叠的概率增加。

3）该算法对电网的初始信号没有约束，不需要获取电网的初始参数，具有很好的动态特性和自适应性。该算法可以实现电网中特定次谐波检测。

4）对仿真数据和实测数据验证的结果表明，该算法可用于电网的谐波检测，且具有很好的精度。

［1］肖湘宁.电能质量分析与控制［M］.北京：中国电力出版社，2004.

［2］黄纯，朱智军，曹一家，等.一种电网谐波与间谐波分析新方法［J］.电工技术学报，2013，28（9）：32-39.

［3］程志友，程晨，付学敏，等.基于共轭-旋转矢量不变性技术的谐波检测方法［J］.电工技术学报，2013，28（5）：274-279.

［4］熊杰锋，李群，袁晓冬，等.电力系统谐波和间谐波检测方法综述［J］.电力系统自动化，2013，37（11）：125-133.

［5］Akagi H，Kanazawa Y，Nabae A.Instantaneous Reactive Pow⁃er Compensators Comprising Switching Devices Without Ener⁃gy Storage Components［J］.IEEE Transactions on Industry Applications，1984，20（3）：625-630.

［6］曾瑞江，杨震斌，柳慧超，等.基于小波变换的电力系统谐波检测方法研究［J］.电力系统保护与控制，2012，40（15）：35-39.

［7］舒泽亮，郭育华，连级三，等.基于小波包多频带分解实现谐波抑制与无功补偿［J］.中国电机工程学报，2006，26（21）：82-87.

［8］喻翌，赵海全，何正友，等.基于ANCT和Adaline两种自适应谐波电流检测模型的分析［J］.电力系统保护与控制，2013，41（16）：71-77.

［9］杨建宁，陈婕，关佳军，等.一种改进变步长的自适应谐波检测算法［J］.电力系统保护与控制，2011，39（16）：40-44.

［10］王凯亮，曾江，王克英，等.一种基于BP神经网络的谐波检测方案［J］.电力系统保护与控制，2013，41（17）：44-48.

［11］牛胜锁，梁志瑞，张建华，等.基于三谱线插值FFT的电力谐波分析算法［J］.中国电机工程学报，2012，32（16）：130-136.

［12］王刘旺，黄建才，孙建新，等.基于加汉宁窗的FFT高精度谐波检测改进算法［J］.电力系统保护与控制，2012，40（24）：28-33.

［13］Huang N E.The Empirical Mode Decomposition and the Hil⁃bert Spectrum for Nonlinear and Non⁃stationary⁃time Series Analysis［J］.Proceedings of the Royal Society A，1998，454（1971）：903-995．

［14］Wu Z，Huang N E．A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method［J］. Proceedings of the Royal Society A，2004，460（2046）：1597-1611．

［15］Wu Zhaohua，Huang N E．Ensemble Empirical Mode Decom⁃position：a Noise⁃assisted Data Analysis Method［J］.Advanc⁃es in Adaptive Data Analysis．2009，1（1）：1-41．

［16］朱宁辉，白晓民，董伟杰，等.基于EEMD的谐波检测方法［J］.中国电机工程学报，2013，33（7）：92-98.

［17］于兴林，李慧敏，李天云，等.基于EEMD和TLS-ESPRIT的谐波间谐波检测方法［J］.电力系统保护与控制，2014，42（4）：67-72.

Harmonic Detection Method Based on Frequency Constraining Empirical Mode Decomposition

LI Yue⁃ying1，2，LIN Jia⁃quan2，LI Zong⁃shuai2
（1.Aerospace and Automotive Institute，Tianjin Sino⁃german Vocational Technical College，Tianjin 300350，China；2.Aerontatical Automation College，Civil Aviation University of China，Tianjin 300300，China）

Mode mixing often ocurrs while using empirical mode decomposition（EMD）in harmonic detection.To solve the problem，a new EMD algrothim was proposed based on frequency constrain.By frequency constrainting the distribution of zero points in intrinsic mode function（IMF）and redesigning the screening criteria，the occurrence probability of mode mixing was reduced.Simulation researches of harmonic detection had been done seperatly，which were based on frequency constraint EMD method，the traditional EMD method and instantaneous reactive power method（p-q method）.The result shows that the improved algrothim could overcome the mode mixing problem in traditional EMD，detect the fundamental current and the spetific harmonic effectively and get better detection accuracy and the consistency of the fundamental current phase than p-q method.The algrothim work better in harmonic decomposition to be of good prospects in application.

empirical mode decomposition（EMD）；harmonic detection；intrinsic mode functions（IMF）；mode mixing

TM761

A

2014-10-13

修改稿日期：2015-07-03

国家自然科学基金民航联合基金（U1433107）

李月英（1982-），女，硕士研究生，Email：sdulyy2000@126.com