改进细菌群体趋药性算法在无功优化中的应用

任新伟，徐建政

（山东大学电气工程学院，济南250061）

改进细菌群体趋药性算法在无功优化中的应用

任新伟，徐建政

（山东大学电气工程学院，济南250061）

为了克服细菌群体趋药性BCC（bacterial colony chemotaxis）算法容易陷入局部最优的缺点，在自适应调整细菌移动速度和感知范围的基础上引入了混沌优化。先将部分重叠或者陷入局部极值点的菌群映射为混沌序列，使其可以重新更优质的遍历分布于空间；然后通过逆映射得到菌群新的适应度值，提高了算法的全局搜索能力，并成功将其应用到电力系统的无功优化中；对Rastrigin函数进行仿真以及IEEE33节点配电系统进行计算分析。结果表明改进的算法具有很好的全局搜索能力，能有效降低系统有功网损，该算法是可行的。

配电网；无功优化；细菌群体趋药性算法；混沌映射；全局最优

随着电网规模日益扩大，负荷需求不断增长，如何在满足负荷发展需要的前提下，充分利用系统的无功资源，保证系统的安全、经济运行，多年来一直是国内外电力工作者们致力研究的课题。通过控制无功的合理流动，可以有效降低配网网损并提高电压调整能力，这对于电网的经济可靠运行有着重要的意义[1-3]。

无功优化问题是指某电力系统在一定运行方式下，满足各种约束条件，达到预定目标的优化问题，它涉及无功补偿装备投入地点的选择、无功补偿装置投入容量的确定、变压器分接头的调节和发电机机端电压的配合等。所以，配电网无功优化通常是多变量、多约束的混合非线性规划问题。目前，一些新型的人工智能优化方法如遗传算法[4-5]、进化算法[6]、细菌趋药性算法、混沌搜索、Tabu搜索[7]、粒子群算法[8-9]等已经取得了一定的成果。但是，任何一种算法都不可能在所有方面都占优势，比如遗传算法有很好的收敛性，计算时间少，鲁棒性高，但不能很好地解决大规模计算量问题，并且容易陷入“早熟”；粒子群算法比遗传算法规则更为简单，更容易实现、精度高、收敛快，但其容易陷入局部最优。所以，构造混合算法或者寻求各种算法的有机结合是未来研究的方向。

细菌群体趋药性BCC（bacterial colony chemo-taxis）算法规则简单，容易实现，同时，可以感知外界环境的变化来改进自己菌群的位置，所以在一定程度上加速了其收敛能力，但也存在着容易陷入局部最优的缺点。本文在动态调整细菌的移动速度和感知范围的基础上，通过与混沌算法相结合，引入了混沌映射，使得菌群可以更优质地遍历性分布，提高了全局搜索能力。并建立了配电网无功优化模型，通过算例分析，表明了算法的有效性。

1 配电网无功优化模型

1.1 目标函数

以无功补偿设备的出力QC为控制变量、负荷节点电压为状态变量、配电网有功网损最小为目标建立优化模型，把负荷节点电压越界作为罚函数，即

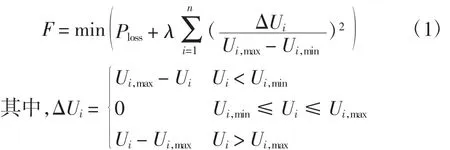
式中：Ploss为系统有功网损；λ为电压越限罚系数，本文取为1；n为负荷节点数；Ui，max和Ui，min分别为节点电压的上下限，分别取为1.03和0.93。

1.2 约束条件

潮流方程等式约束条件为

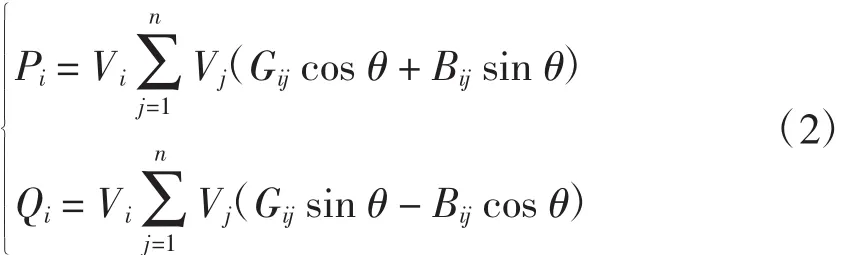
式中：Pi、Qi分别为节点i的注入有功和无功功率，Gij、Bij、θ分别为节点i、j之间的电导、电纳和节点电压相角差。

控制变量不等式约束条件为

状态变量不等式约束条件为

式中，QCmax、QCmin分别为无功补偿设备的无功容量的上下限。

2 基本BCC算法及改进方法

2.1 基本BCC算法

2.1.1 趋化过程

（1）给定计算精度ε，设定系统参数T0、b、τC。（2）计算细菌的移动速度v，设其为常数。

（3）计算细菌新的移动轨迹和移动时间。

细菌在n维空间移动时，可用n-1维角度向量φ=（φ1，φ2，…，φn-1）来描述其方向。其向左或向右偏转的方向与原轨迹的夹角由高斯概率密度分布确定，即

细菌在新轨线上的移动时间τ由指数概率分布决定，即

其中，T值与系统参数T0、b有关，即

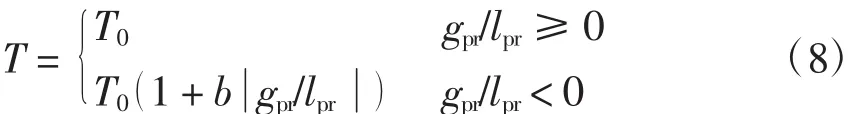
式中：T0为最小平均移动时间；b为与维数无关的参数。

（4）计算新位置。

细菌在n维空间中的移动步长L=（l1，l2，…，ln-1），其中

把新确定的移动步长与之前的坐标求和，就可以得到细菌的新位置。

2.1.2 感知过程

细菌在移动之前，会感知外界的信息，主动向更好的位置靠近。定义移动步数为k时细菌所能感知的同伴中心点为

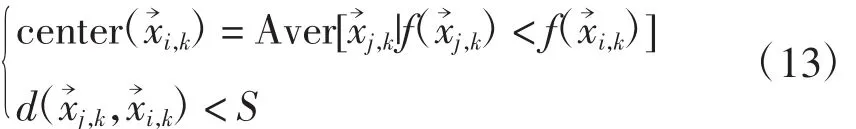
2.2 改进方法

BCC算法是在BC算法中加入信息交互机制而来[10]，菌群之间相互交换信息，可以加快收敛速度，但同时不可避免地会容易产生局部最优。

在基本BCC算法的基础上[11-13]，动态调整细菌运动速度v和感知范围Sk，即

从式（14）可知，自适应调整细菌移动速度无非就是随着迭代次数的增加，细菌的速度减小，但与菌群的位置无关，当细菌陷入局部极值或者部分重叠的时候，无法通过速度的调整来跳出这些区域；而式（15）中，考虑到当代个体与当代其他个体之间的距离关系和差别程度，可以使得个体在算法初期很快地往优秀的方向移动，而随着个体之间距离的缩小，感知范围缩小，不能阻止菌群陷入局部最优，或者当其陷入局部最优时无法有效地跳出。当菌群部分重叠或者陷入局部最优后的n次迭代中，细菌几乎不再移动，个体之间的距离几乎不再变化，这时自适应调整就失去了意义。所以仅靠自适应调整移动速度和感知范围并不能很好地解决算法容易陷入局部最优的问题。

本文引入混沌映射，利用其规律性和遍历性使菌群可以重新优质遍历分布于搜索空间。具体方法如下。

（1）判断何时引入混沌映射。因为当菌群重叠或者陷入局部最优时，细菌移动距离很小，根据式（15）的启发，可以取当代的一个细菌（第n代）与前面m代（n-1，n-2，…n-m）中同一个细菌位置之间的距离作为判据，即

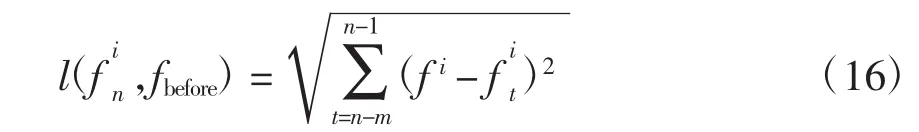
（2）假设需要进行混沌优化的细菌数目为s，对细菌的适应度值进行混沌优化。

利用Logistic映射来产生混沌现象，即

当μ∈[3.57，4]，xk∈（0，1），xk≠（0.25、0.5、0.75）时，可以得到混沌现象，此时xk会遍历空间（0，1）。

取s个细菌的最优适应度值f，首先将其映射到Logistic方程的定义域（0，1），即

式中，fmax、fmin分别为适应度值的上、下限。再利用式（17）多次迭代计算得到s个混沌序列变量，最后把此混沌序列通过逆映射得到s个新的适应度值，

这样上述s个重叠或陷入局部最优的细菌就重新遍历于空间。

文献[10]引入的Logistic映射，只是对单个值进行一下变换，本来重叠的个体经过同一个公式的变换仍然会重叠，而且没有通过迭代产生混沌序列，没法使得菌群遍历于空间（只有定义域在（0，1）的值经过反复迭代才可以遍历于（0，1）空间），谈不上是混沌迁移。

为了验证算法跳出局部最优的能力，本文用未引入混沌映射和引入混沌映射算法分别对Rastrigin函数进行20次仿真，函数表达式为

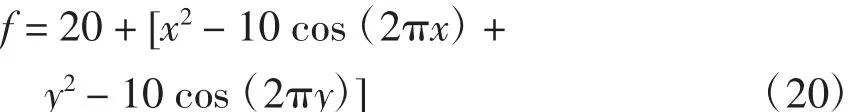
其中（x，y）∈（-20，20）。在进行20次仿真实验后，加入混沌优化的算法，在细菌移动20步之后，均可以找到最优解，如图1所示；未加入混沌优化的算法中，有5次陷入局部最优；3次还没有找到最优解。由此可得，加入混沌映射后，函数寻优成功率为100%，防止了算法陷入局部最优，提高了其全局搜索能力，同时，算法的收敛能力大大增强，在少于20步就可以找到最优解。

2.3 算法的实现步骤

算法的实现步骤如下。

图1 菌群移动20步之后的分布情况Fig.1Distribution of flora after 20 steps

（1）设系定统参数，初始化菌群。设定计算精度εbegin和εend的值趋化过程中精度实时更新εnew= ε/μ，设定最大迭代次数M。

（2）计算初始配电网系统的电压水平和网损，用于调用比较。

（3）利用趋化过程和感知过程，分别得到2次目标函数值，取较小的一个记为fbetter，位置记为xbetter。

（4）从第3代之后开始检测，如果某些细菌符合混沌映射的条件，说明产生了部分重叠的个体，此时对菌群进行混沌优化，使其跳出重叠区域。

（5）进化操作和精英保留策略，记录最优值。

（6）循环计算，直到达到精度要求或迭代次数上限。

图2 IEEE33节点系统Fig.2IEEE33-node system

3 算例分析

采用MatlabR2009a对IEEE33节点系统进行无功优化计算，系统线路参数保持不变[14]，其网络结构如图2所示，并假设在节点2、6、13、31补偿电容器。选取三相功率的基准值为100 kVA，线电压基准值为12.66 kV，设节点1为平衡节点，负荷节点范围为[0.93，1.03]。设定细菌种群数为50，最大迭代次数为500，精度系数εbegin=2.0，εend=0.001，精度更新系数μ=1.25，优化结果取20次的计算平均值。

3.1 优化结果分析

经过优化分析，优化结果如表1和表2所示。

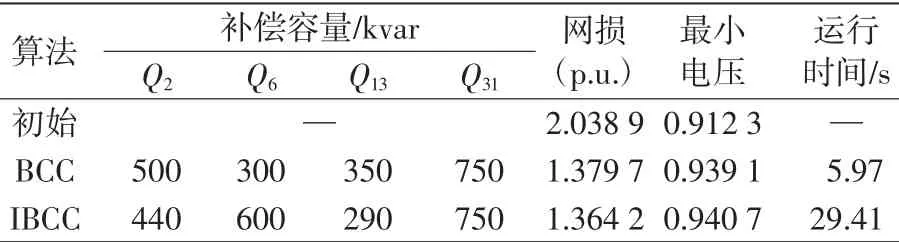
表1 不同算法的优化结果Tab.1Optimization results of different methods

表2 优化前后节点电压Tab.1Node voltage before and after optimization p.u.

由表1可知，经过优化后，系统网损大大降低，最小电压由0.912 3 p.u.提高到0.940 7 p.u.。虽然改进算法的运行时间较长，但是其寻优成功率为100%，全局搜索能力更强。

从表1和表2可知，经过无功优化以后，节点电压水平升高，并且利用改进算法的优化效果更加明显。优化前，系统电压越限个数为13个，由于目标函数中罚函数的引入，优化后的电压结果都在合理的范围以内。

综合算例分析计算和对Rastrigin函数仿真结果，改进的算法在网损减小和电压改善方面的效果更加明显，同时能防止陷入局部最优，全局搜索和收敛能力更强，所以此算法具有很好的研究意义。

4 结论

（1）改进了BCC算法，在自适应调整细菌移动速度和感知范围的基础上引入混沌映射，有效地平衡了算法跳出局部最优和寻优速度之间的关系。

（2）通过无功优化有效地降低了系统有功网损，同时提高了电压水平，但优化模型中只考虑了有功网损最小，没有把电压稳定度等指标加入其中，在后续研究中，应考虑建立一个多目标模型，更加全面地对系统进行优化。

[1]陈树勇，宋书芳，李兰欣，等（Chen Shuyong，Song Shufang，Li Lanxin，et al）.智能电网技术综述（Survey on smart grid technology）[J].电网技术（Power System Technology），2009，33（8）：1-7.

[2]王建，李兴源，邱晓燕（Wang Jian，Li Xingyuan，Qiu Xiaoyan）.含有分布式发电装置的电力系统研究综述（Power system research on distributed generation penetration）[J].电力系统自动化（Automation of Electric Power System），2005，29（24）：90-97.

[3]张沈习，程浩忠，张立波，等（Zhang Shenxi，Cheng Haozhong，Zhang Libo，et al）.含风电机组的配电网多目标无功规划（Multi-objective reactive power planning in distribution system incorporating with wind turbine generation）[J].电力系统保护与控制（Power System Protection and Control），2013，41（1）：40-46．

[4]Deb K，Pratap A，Agarwal S，et al.A fast and elitist multiobjective genetic algorithm：NSGA-II[J].IEEE Trans on Evolutionary Computation，2002，6（2）：182-197.

[5]张文，刘玉田（Zhang Wen，Liu Yutian）.自适应粒子群优化算法及其在无功优化中的应用（Adaptive particle swarm optimization and its application in reactive power optimization）[J].电网技术（Power System Technology），2006，30（8）：19-24．

[6]刘自发，张建华（Liu Zifa，Zhang Jianhua）.一种求解电力经济负荷分配问题的改进微分进化算法（An improved differential evolution algorithm for economic dispatch of power systems）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（10）：100-105．

[7]刘玉田，马莉（Liu Yutian，Ma Li）.基于Tabu搜索方法的电力系统无功优化（Reactive power optimization based on Tabu search approach）[J].电力系统自动化（Automation of Electric Power Systems），2000，24（1）：61-64．

[8]张劲松，李崎强，王朝霞（Zhang Jinsong，Li Qiqiang，Wang Zhaoxia）.基于混沌搜索的混和粒子群优化算法（Hybrid particle swarm optimization algorithm based on the chaos search）[J].山东大学学报：工学版（Journal of Shandong University：Engineering Science），2007，37（1）：47-50，114．

[9]俞俊霞，赵波（Yu Junxia，Zhao Bo）.基于改进粒子群优化算法的最优潮流计算（Improved particle swam optimization algorithm for optimal power flow problems）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（4）：83-88．

[10]赵义术，李磊，王大鹏（Zhao Yishu，Li Lei，Wang Dapeng）.基于细菌群体趋药性的电力系统无功优化（Power system reactive power optimization based on the bacterial colony chemotaxis）[J].继电器（Relay），2007，35（16）：50-54．

[11]陈继明，王元元，高艳亮（Chen Jiming，Wang Yuanyuan，Gao Yanliang）.基于改进细菌群体趋药性算法的配电网无功优化（Reactive power optimization of distribution network based on improved bacterial colony chemotaxis algorithm）[J].电力系统保护与控制（Power System Protection and Control），2012，40（14）：97-102．

[12]张晓辉，卢志刚，秦四娟（Zhang Xiaohui，Lu Zhigang，Qin Sijuan）.基于改进细菌群体趋药性算法的电力系统无功优化（Reactive power management based on improved bacterial colony chemotaxis algorithm）[J].电网技术（Power System Technology），2012，36（2）：109-114．

[13]李秀卿，孙守鑫，张超（Li Xiuqing，Sun Shouxin，Zhang Chao）.基于改进细菌群体趋药性算法的无功优化（Reactive power optimization based on the improved bacterial colony chemotaxis algorithm）[J].电力系统保护与控制（Power System Protection and Control），2011，39（8）：56-59．

[14]王守相，王成山.现代配电系统分析[M].北京：高等教育出版社，2007．

Application of Improved Bacterial Colony Chemotaxis Algorithm in Reactive Power Optimization

REN Xinwei，XU Jianzheng
（School of Electrical Engineering，Shandong University，Jinan 250061，China）

In order to tackle the shortcoming of the bacterial colony chemotaxis algorithm that is liable to fall into local optimum，this paper introduces chaotic optimization on the basis that the perception range and the speed of movement of bacteria are adjusted adaptively.This paper initiallyfirstly maps bacteria which overlap or get into local extreme point onto chaotic sequence，making them in ergodic and superior distribution again，then gets the new fitness value through the inverse mapping which improves the global search capability，and applies the improved algorithm to reactive power optimization successfully.Simulation results of Rastrigin function and analysis of IEEE33 bus system showindicate that the improved algorithm is goodbetter in global search capability and can effectively reduce the network loss，so it is feasible.

distribution network；reactive power optimization；bacterial colony chemotaxis algorithm；chaos modelapping；global optimum

TM71

A

1003-8930（2015）05-0081-05

10.3969/j.issn.1003-8930.2015.05.15

任新伟（1988—），男，硕士研究生，研究方向为电力系统运行与控制。Email：sinways@163.com

2013-06-24；

2013-07-09

徐建政（1956—），男，硕士，教授，研究生导师，研究方向为电力系统运行与控制以及计算机在电力系统中监控中的应用。Email：xujianzheng@sdu.edu.cn