采用最大-最小蚁群算法的励磁系统参数辨识

毛晓明，蔡永智，赵勇

（1．广东工业大学自动化学院，广州510006；2．中国南方电网科学研究院，广州510080）

采用最大-最小蚁群算法的励磁系统参数辨识

毛晓明1，蔡永智1，赵勇2

（1．广东工业大学自动化学院，广州510006；2．中国南方电网科学研究院，广州510080）

为获得发电机励磁系统准确的模型参数，对BPA（bonneville power administration）软件中励磁系统典型仿真模型进行深入分析，得到模型参数与励磁系统大、小阶跃响应特性的关联关系。结合实际情况，对需辨识参数进行筛选，对参数取值范围进行限制。采用最大-最小蚁群算法对参数进行辨识，先求得影响发电机空载电压小干扰阶跃响应特性的主要参数，再得到影响发电机空载电压大干扰阶跃响应特性的主要参数。BPA计算得到的辨识模型仿真曲线与实测数据吻合良好，仿真结果表明了辨识方法的有效性。

励磁系统；参数辨识；最大-最小蚁群算法；电压阶跃响应

电力系统规划及运行方式的制定，有赖于电力系统仿真计算与分析[1]。励磁系统模型是同步电机模型的重要组成部分，其参数的准确性对电力系统稳定性计算的精度和结论有重要影响。对发电机励磁系统进行相关实验，根据现场采集的数据进行励磁系统参数辨识是一项非常重要的工作[2]。

励磁系统参数辨识的方法主要有传统辨识法和人工智能法。常用的传统辨识法有频域法[3]和时域法[4-5]，这两种方法概念清晰，简便易行，在工程上得到了广泛应用。但励磁系统存在高阶非线性环节，应用传统辨识法难以取得令人满意的效果。人工智能法具有强鲁棒性和良好的全局寻优能力，能有效解决高阶非线性系统辨识难的问题。目前使用最多的人工智能方法为遗传算法GA（genetic algorithm）。文献[6-7]将GA及其改进算法应用于励磁系统参数辨识，结果较为理想。但GA寻优效果依赖于参数初值的选定，在先验知识不足时难以辨识出与实际相符的系统参数。

本文以仿真软件BPA中的励磁系统标准模型为待辨识模型，根据发电机空载大、小干扰电压阶跃响应实测数据，采用最大-最小蚁群算法辨识励磁系统模型参数，实现了励磁系统原始模型与BPA标准模型的转换。该方法有效解决了传统辨识法对高阶非线性系统辨识难的问题，同时算法只需给出参数的取值范围，与遗传算法相比，对先验知识的依赖更少。

1 最大-最小蚁群算法的基本原理

蚁群算法ACO（ant colony optimization）[8]由意大利Dorigo于1992年提出，是一种种群寻优的启发式搜索算法[8]。在此基础上，德国Stutzle[9]提出最大-最小蚁群算法MMAS（maximum minimum ant system）[9]。以平面上的旅行商问题TSP（travelling salesman problem）为例，阐述MMAS的原理。

假设城市数为m，城市i、j的距离为lii，路径（i，j）上的初始信息素δij（0）为常数。循环开始时，将n只蚂蚁随机置于m个城市，蚂蚁k从城市i出发，按照概率选择下一个要转移的城市j，其转移概率为

式中：θij为启发因子，θij=1/lij；allowedk为蚂蚁k下一步允许选择的城市；指数α、β为信息素与启发信息的相对重要性。

当蚂蚁完成一次循环，即：遍历所有城市后，MMAS记录当前循环最短路径，只对当前循环中找到最优解的那只蚂蚁，或实验开始以来找到最优解的那只蚂蚁进行信息素更新，并进入下一次循环。更新规则为

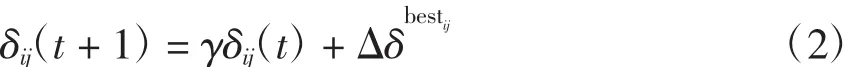
式中：δij为当前循环最优路径（i，j）的信息素；γ为信息素残留度，0〈γ〈1；Δδbestij为蚂蚁k走过路径（i，j）上的信息素增量，为当前循环最优路径长度。

为避免搜索停滞，MMAS引入信息素上下限限制机制。将每条路径上的信息素轨迹量限制在[δmin，δmax]。δmax和δmin的计算公式为

式中：f（sopt）为当前全局最优路径长度；e为在每个选择点上待选解的平均个数；Pbest为当MMAS收敛时蚂蚁构造出最优路径的概率。信息素轨迹量在第1次循环后均被置为δmax（1），即为第1次循环后的信息素上限。

此外，MMAS还引入了信息素平滑机制，即

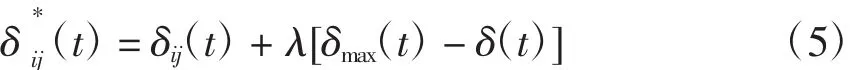
式（5）用于提高蚂蚁搜索新解的能力，其中，0〈λ〈1。当MMAS非常接近收敛时，该机制有助于增加非收敛路径的信息素轨迹量。

2 基于MMAS的励磁系统参数辨识

2.1 励磁系统的数学模型

南方电网辖区发电机大多采用交流励磁机系统和自并励静止励磁系统，其在BPA仿真环境中分别采用FR和FV模型，见图1和图2。

根据南方电网《同步发电机励磁系统参数实测与建模导则》，励磁系统小干扰阶跃性能指标仿真校核误差应满足表1的要求。

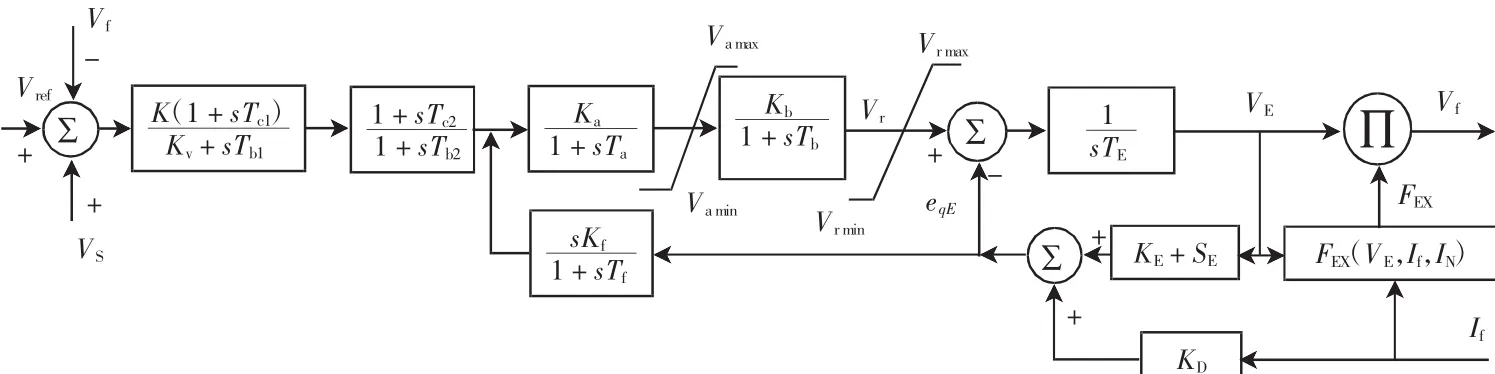
图1 交流励磁机系统的FR模型Fig.1FR model of AC excitation system

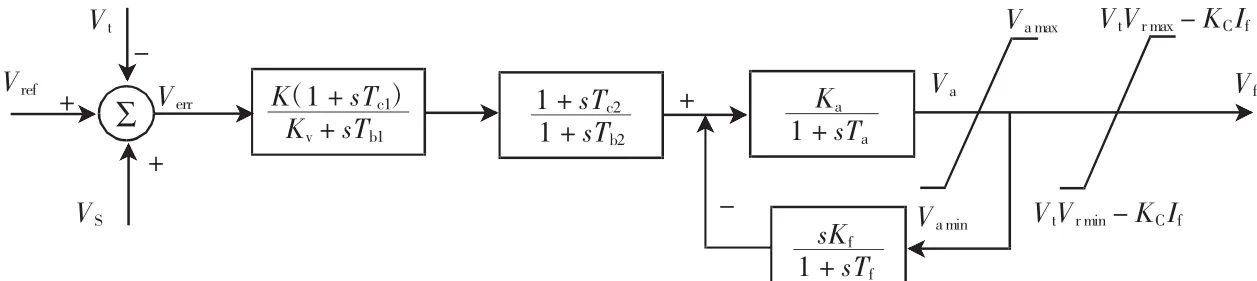
图2 自并励静止励磁系统的FV模型Fig.2FV model of static excitation system

表1 励磁系统性能指标的仿真校核误差Tab.1Checking tolerance of excitation system performance

2.2 系统辨识的原理及数学模型

系统辨识是指根据系统的输入、输出信号，采取某种辨识方法估计系统的数学模型及其参数。其原理如图3所示。

图3 系统辨识原理Fig.3System identification principle

图3中，x为输入信号，yr和ym分别为实际系统和模型系统的输出响应，J为辨识误差e（t）的评价函数。辨识即采用某种算法不断迭代修正系统模型及其参数，使J（e（t））达到最小为止。

按照对待测系统的了解程度，可将系统分为“黑箱”系统、“灰箱”系统和“白箱”系统。励磁系统属于“灰箱”系统，可按物理机理先得到数学模型，再用系统辨识方法确定模型参数[10]。本文根据励磁系统参数对发电机空载大、小干扰阶跃响应的影响，分2步进行参数辨识。

（1）辨识励磁系统除限幅环节以外的参数。以发电机端电压空载小干扰阶跃响应实测输出与仿真输出误差e（t）的时间乘绝对误差积分准则ITAE（integral of time-weighted absolute error）作为辨识的目标函数，即

式中：c为机端电压的采样点，c=1，2，…，N；tc为采样时间间隔。

（2）对限幅环节参数进行辨识。目标函数为

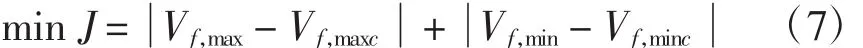
式中：Vf，max、Vf，min分别为发电机空载大干扰阶跃响应仿真得到的正向、反向顶值励磁电压；Vf，maxc、Vf，minc分别为发电机空载大干扰阶跃响应实验的实测正向、反向顶值励磁电压。

式（6）、式（7）中，待辨识参数的取值区间为[50%厂家值，150%厂家值]。

2.3 参数辨识的算法实现

以自并励静止励磁系统为例说明，图2中K取1。通过仿真分析，得到影响发电机空载小干扰阶跃响应的模型参数为Ka、Tc1、Tb1、Kv、Tc2、Tb2、Kf和Tf，影响发电机空载大干扰阶跃响应的模型参数为Vrmax、Vrmin。励磁系统调节器响应时间Ta的数量级一般为ms，对发电机空载扰动阶跃响应的影响很小；Vamax、Vamin较大，在发电机大干扰阶跃响应实验中，励磁系统输出一般不会达到其限值；换相压降系数KC较小，对限幅值影响不大。辨识时将Ta、Vamax、Vamin和KC设为厂家值。

类似于蚁群算法在TSP问题上的路径搜索，除限幅环节以外的参数按照排列顺序可视作A1～A8共8个解层区。根据每个参数的取值范围，分别以rA1～rA8为间隔划分解层区A1～As，每个解层区有nA1～nA8个解元素，如图4所示。在每只蚂蚁开始搜索前，Ka、Kc1、Kb1、Kv、Kc2、Kb2和Kf均置为1，Tf置为0。开始时，蚂蚁k向A1层跳转，按照概率转移公式计算A1层各个解元素的转移概率，，…，；随机生成一个在（0～1）区间内满足均匀分布的随机数P，与选择概率P1，P2，…，PnA1依次比较，以当前选择概率大于P对应的解元素作为X1（其中，P1=Pa11，，这时蚂蚁k到达A1层。重复上述步骤，蚂蚁k可依次跳转至A2～A8层并确定X2～X8，从而得到一组解X= [X1，X2，…，X8]。记录每次循环最优解的值，当循环结束后，循环最优解集的最小值即为全局最优解。

对于限幅环节参数Vrmax、Vrmin的辨识，解层数可视为两层，做法同上。限幅环节初值置为0，其他参数设定为前述辨识得到的结果。

为提高MMAS的算法性能，引入蚁群系统的概率转移规则。1只位于节点i的蚂蚁按规则选择下一个将要移动到的节点j，规则为

式中：q为[0，1]区间均匀分布的随机数；q0为一个给定的参数（0≤q0≤1）；jS为按照式（1）给出的概率分布所选出的节点[9]；θij=1/Jij=1/（Jj-Ji），Ji为计及第1～i层节点X1～Xi时目标函数的大小。当Jij较小时，θij较大，转移概率也较大，使得蚂蚁每一步倾向于寻找使系统实际输出与仿真输出误差最小的参数。A8层中各点对应的J8x即为目标函数J的值，故直接选取J8x较小的X8，无需根据转移概率来选择。具体流程见图5。算法初始化包括：输入待辨识参数的取值范围；置蚂蚁个数n为10，最大循环数Nc为30，概率转移公式相关参数α为1，β为2，q0为0.45，γ为0.98；用于计算信息素下限的相关参数：Pbest为0.5信息素平滑参数λ=0.5；蚂蚁初始位置为零点，各路径初始信息素δij（0）为1 000，当前循环次数Nc为1。

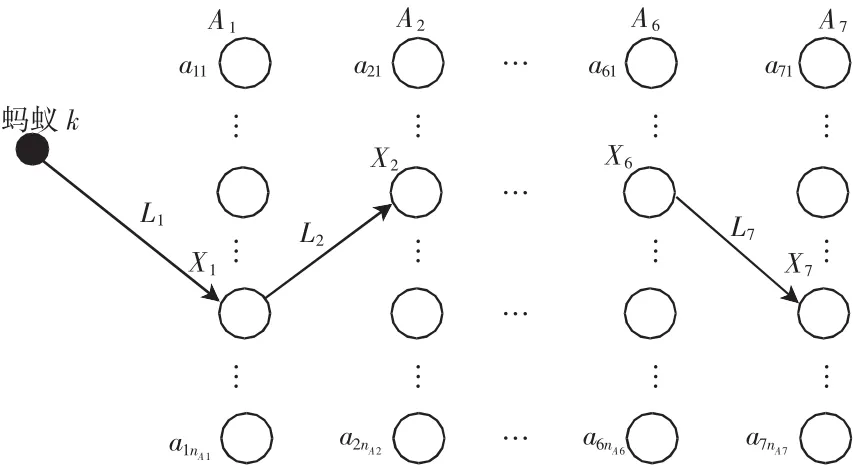
图4 分层求解Fig.4Layered solution

在辨识出最优解X*=[X1*，X2*，…，X8*]后，再以[Xi*-rAi，Xi*-rAi]（i=1～8）作为待辨识参数的取值范围，以rBi为间隔对其进行等分（本文取rBi=rAi/10），可得到更精确解。对于励磁系统参数，一般只需对其辨识范围做2次划分即可满足精度要求。

交流励磁机励磁系统的参数辨识方法及步骤与自并励励磁系统类似，区别仅在于待辨识参数（解层区）数目不同，不再赘述。

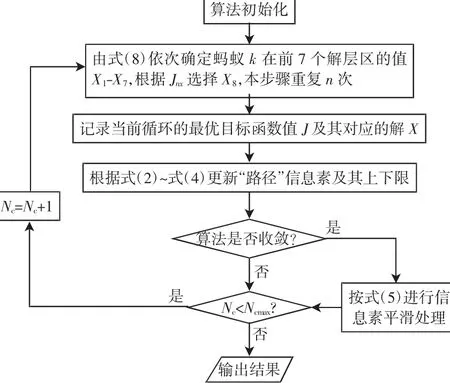
图5 参数辨识流程Fig.5Flow chart of parameter identification

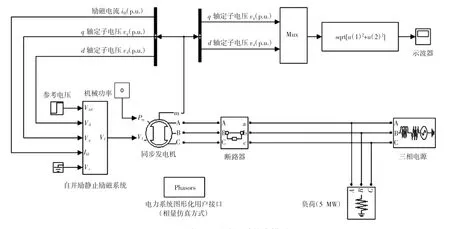
图6 单机-无穷大系统仿真模型Fig.6Single machine-infinite bus simulation model

3 算例

本文在Matlab仿真环境中搭建如图6所示的单机-无穷大电力系统仿真模型。发电机采用机组实际参数，采用第1节和第2节所述辨识原理和算法对南方电网辖区多台机组励磁系统参数进行辨识，得到BPA标准模型参数。

以某电厂1号机组为例，其励磁系统为自并励静止励磁系统，原始模型如图7示。在Matlab中搭建图2的FV型励磁系统仿真模型。根据原始模型结构，先设置参数Kf=0，Tf=100 s，K=1，再按照第2.3节所述算法，根据发电机空载小、大干扰阶跃响应实测曲线和数据进行辨识计算。辨识结果为：Ka=150.6，Tc1=1 s，Tb1=3.9 s，Tc2=1 s，Tb2=1 s，Kv=1.1，Vrmax=7.6，Vrmin=-6.6。现场装置实际整定参数值为：Ka=156，Tc1=1 s，Tb1=4 s，Tc2= 1 s，Tb2=1 s，Kv=1，Vrmax=7.31，Vrmin=-6.45，辨识值与实际值很接近。

采用辨识模型，在BPA仿真环境中计算机组空载电压5%小干扰阶跃响应，仿真结果与实测结果的比较见图8，主要性能指标比较见表2。可见，励磁系统各项性能指标误差在要求范围内。

由辨识模型计算得到的顶值励磁电压Vfmax= 2.26、Vfmin=-1.9，与机端电压40%大干扰阶跃实验得到的顶值励磁电压Vfmax=2.27，Vrmin=-2.0相符。同理，对南方电网辖区多台机组的励磁系统参数进行辨识，相关性能指标均满足导则要求。

图7 励磁系统原始模型Fig.7Original model of excitation system

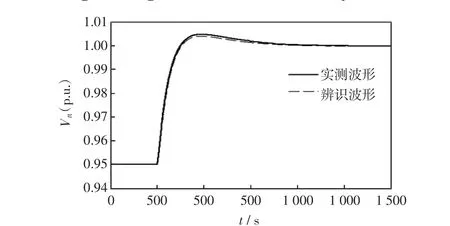
图8 辨识模型5%小干扰阶跃响应与实测结果比较Fig.8Comparison of response of the identified model and field data with a 5%voltage-step

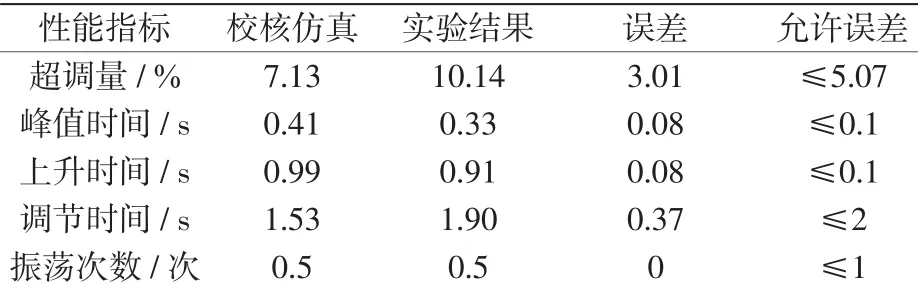
表2 励磁系统5%小干扰阶跃响应误差校核Tab.2Error checking for excitation system response following 5%voltage-step

4 结语

本文提出一种基于最大－最小蚁群算法的励磁系统参数辨识方法，对南方电网辖区多台机组励磁系统参数进行辨识，得到了满足励磁系统性能指标误差要求的BPA标准模型参数。该方法原理简单，方便易行，为辨识励磁系统模型参数提供了新方法。

[1]刘取．电力系统稳定性及发电机励磁控制[M]．北京：中国电力出版社，2007.

[2]舒辉，文劲宇（Shu Hui，Wen Jinyu）．发电机励磁系统参数辨识综述（Overview of parameter identification methods for generator excitation systems）[J]．电力自动化设备（Electric Power Automation Equipment），2008，28（2）：104-107．

[3]郭睿，王修庞，郭珊珊，等（Guo Rui，Wang Xiupang，Guo Shanshan，et al）．基于相关辨识法的发电机励磁系统参数辨识（The estimation of generator excitation system parameters based on correlation identification method）[J]．继电器（Relay），2008，36（5）：19-22．

[4]朱守真，沈善德，焦连伟，等（Zhu Shouzhen，Shen Shande，Jiao Lianwei，et al）．建立大型同步发电机组励磁系统动态参数（Establishing the excitation system dynamic parameters for large synchronous generators）[J]．中国电机工程学报（ProceedingsoftheCSEE），1997，17（3）：179-183．

[5]曹浩军，张承学，单勇（Cao Haojun，Zhang Chengxue，Shan Yong）．基于LIF法的励磁系统参数辨识（IdentificationofexcitationsystemparametersbasedonLIFmethod）[J]．继电器（Relay），2004，32（15）：5-9．

[6]王晓伟，蒋平，曹亚龙，等（Wang Xiaowei，Jiang Ping，Cao Yalong，et al）．改进遗传算法在发电机励磁系统参数辨识中的应用（Application of improved genetic algorithm in parameter identification of generator excitation systems）[J]．继电器（Relay），2007，35（11）：16-20．

[7]王兴贵，王言徐，智勇，等（Wang Xinggui，Wang Yanxu，Zhi Yong，et al）．遗传算法在发电机励磁系统参数辨识中的应用（Application of genetic algorithm in generator excitation system parameters identification）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（1）：76-79．

[8]Dorigo M，Di Caro G，Gambardella L M．Ant algorithms for discrete optimization[J]．Artificial Life，1999，5（2）：137-172．

[9]李士勇．蚁群算法及其应用[M]．哈尔滨：哈尔滨工业大学出版社，2004．

[10]沈善德．电力系统辨识[M]．北京：清华大学出版社，1993．

Excitation System Parameter Identification via Maximum-minimum Ant System

MAO Xiaoming1，CAI Yongzhi1，ZHAO Yong2
（1．Faculty of Automation，Guangdong University of Technology，Guangzhou 510006，China；2．Science Research Academy，China Southern Power Grid，Guangzhou 510080，China）

In order to acquire the accurate parameters of generator excitation systems，the typical simulation models used in bonnevitle power administration BPA software package are analyzed in depth.The relationship between the parameters and system small and large-signal voltage-step response is investigated.Parameters needed to be identified are selected and their ranges of values are specified according to practical status.Selected parameters are identified via the maximum-minimum ant system，and the parameters which mainly impact on generator small-signal voltage step-response are initially obtained，then the parameters dominating generator large-signal voltage step-response are subsequently acquired.Simulation curves of the identified model obtained by BPA fit well with the field data，and results show the effectiveness of the developed method.

excitation system；parameter identification；maximum-minimum ant system；voltage step-response

TM743

A

1003-8930（2015）05-0051-05

10.3969/j.issn.1003-8930.2015.05.10

毛晓明（1971—），女，博士，副教授，研究方向为电力系统运行、分析与控制。Email：mxmsunny@163.com

2013-11-14；

2014-08-14

广东省自然科学基金项目（2014A030313509，S2013010012431,S2013040013776）；广东省教育厅育苗工程项目（2013LYM_0019）

蔡永智（1984—），男，硕士研究生，研究方向为电力系统运行分析与控制。Email：xbcyzsunny@163.com

赵勇（1976—），男，博士，高级工程师，研究方向为电网安全稳定分析与规划工作。Email：5908759@qq.com