一种改进的差分进化算法及其应用

夏莘媛，刘伯颖，李洋，李玲玲

（1.河北工业大学电子信息工程学院，天津 300401；2.河北工业大学计算机与软件学院，天津 300401；3.河北工业大学电气工程学院，天津 300401）

一种改进的差分进化算法及其应用

夏莘媛1，刘伯颖2，李洋3，李玲玲3

（1.河北工业大学电子信息工程学院，天津 300401；2.河北工业大学计算机与软件学院，天津 300401；3.河北工业大学电气工程学院，天津 300401）

多目标优化问题（MOP）存在范围广且人工求解难度大，通过差分进化算法（DE）解决MOP问题具有重要意义．由于常用DE算法性能有限、收敛速度、计算精度和优化能力相互制约，通过改善变异因子、进化机制以及与粒子群算法融合等措施，研究一类基于粒子群优化和DE的混合算法（PSODE），经典优化函数的仿真实验和对比分析，结果表明在高维复杂寻优问题中可以求得高精度解．在实际数字滤波器优化设计中，表明其改进算法在计算精度和运行速度上均能取得满意的应用效果．

差分进化算法；多目标优化；数字滤波器设计

0 前言

在许多情况下，实际优化问题为多个相互影响与限制的目标所构成，因此需要寻求一个融合多个因素的最优解．这种涉及多个目标并求出问题的最优解，即为多目标优化问题（multi-objectiveoptimization problem，MOP）1．人们通常将MOP问题变为单目标优化问题，然后再进行求解2．这样，实际转化成一个高维优化问题．由于MOP问题往往因其方程复杂且目标彼此制约，问题的解也常常不是唯一的，在解空间中任意一点都可视为一个解．为此需要从海量解中寻找最优解，这是常用求解方法难以实现的．

差分进化算法（DifferentialEvolution，DE）是由Storn等[3-4]于1995年提出的，该算法是受自然界优胜劣汰的进化机制启发的一种全局寻优算法，主要通过模拟自然界生物进化机制，包括变异、交叉和选择等基本操作．常用DE算法适合求解各种最优化问题且具有较好的计算精度和收敛性能，并在解决多目标优化问题上得到广泛关注，现在优化领域已成为一个研究热点，比如AbbassHA等人56提出了Pareto前沿DE算法，BabuBV等7利用罚函数及权值系数方法改进了DE算法，文献[8]设计一种双群体DE算法求解约束多目标优化问题，文献[9]采用自适应DE算法求解多约束优化问题等，均取得较为理想的应用效果．

为进一步提高常用DE算法的性能，本文通过改善变异因子、进化机制及与粒子群优化（PSO）算法融合等措施，研究改进的DE算法并进行对比分析，在实际滤波器的优化设计中以期取得满意的应用效果．

1 差分进化算法及其改进

1.1 差分进化（DE）算法描述

自然界中，每种生物的种群都一直经历着优胜劣汰、适者生存的自然选择．DE算法正是受这种进化模式的启发而诞生，其基本进化操作有：变异、交叉和选择；其控制参数有：交叉因子、缩放因子、种群规模及最大进化代数．

DE算法的具体关键环节如下：

1）粒子初始化：产生N个D维的粒子组成种群，记单个个体为χi,Gi=1,2,,N，其中i为个体的标号，G为进化代数．依照式(1)进行粒子初始化．

6）重复进化：保留每代得到的最优解，在给定的进化代数Gn内选出最佳解，并输出结果．

1.2 DE算法的改进

DE算法具有许多优点，但也存在一些不足，比如因固定的变异因子F导致的收敛速度与计算精度相互制约，容易出现早熟现象等．为了改善DE算法性能，本文将做进一步改进．

1.2.1 基于随机变异因子的DE算法（RDE）

在常用DE算法中，由于变异因子始终为固定值，因此在提高收敛速度时会降低计算精度．为此设定变异因子F=rand，即不断地用[0,1]中的随机数作为变异因子．这种改进算法记为随机变异因子DE算法（RDE）．

1.2.2 收敛变异因子差分进化算法（CDE）

由于固定变异因子F在取值较大时可以使DE算法收敛速度提高，在取值较小时可以提高种群个体逼近最优解的精度，因此可以设定一个收敛因子

这里，F1为新的变异因子，Gn为最大进化代数，G为进化代数．随着G的增加，收敛因子成对数形式在1至0的范围内减小，这样变异因子在最初以较大的值使DE算法收敛、逃离局部极值点，在后期受收敛因子影响而不断减小，使种群个体逐步逼近最优解．这样在一定程度上可同时提高收敛速度与计算精度．

1.2.3 基于PSO的DE混合算法（PSODE）

粒子群优化（PSO）算法的具体过程是：先随机生成一个由N个粒子构成的种群，每个单独粒子代表着优化函数的一组解，粒子在D维的空间内寻优，然后每一次迭代中，利用适应度函数fitness对每一个粒子进行评价．通过更新每个粒子的速度与位置，实现对最优解的寻优．

其中：w为惯性权重；c1与c2是加速因子，一般均取2．r1与r2为[0,1]中的随机数．

本文通过结合PSO与DE算法，得到混合算法（PSODE）．首先，PSO与DE两种算法各自在寻优空间内生成独立的种群，进行相应算法的寻优，然后利用fitness比较两种算法每一代种群的适应度，选取适应度高的粒子进行两种算法之间的交叉，这样可以提高算法的收敛速度，同时还可以减少早熟现象的发生．

当PSO算法采用固定惯性因子w时，与DE算法中采用固定变异因子F一样，会出现收敛速度与计算精度相冲突的情况．因此，可以通过式(10)更新．

其中：wmin与wmaχ分别为w的下限与上限；k为控制因子；G与Gn同DE算法一样分别为进化代数与最大进化代数．

当PSODE快速收敛后,若停留在某一最优值上不再变化，即fitnessχiG=fitnessχiG1==fitnessχiGGp,这样仍会产生早熟现象．此时可以重新产生粒子，即生成一个临时向量：

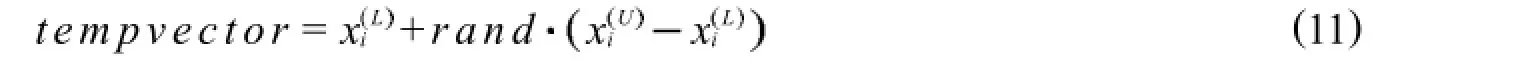
其中：χL与χU同DE算法中的一样为变量的下限与上限；Gp为最大停留的代数．

若tempvector的fitness高于现有粒子的fitness，则用tempvector替换最优粒子；反之，现有粒子不变．

PSODE算法实现过程如下：

Step1设置初始参数：种群数N，最大进化代数Gn，惯性权重的最大值w max和最小值w m in，加速因子c1与c2，控制因子k，变异因子F，交叉因子CR；

Step2初始化PSO算法和DE算法种群：PSOpopulation，DEpopulation；

Step3更新PSOpopulation中粒子的速度和位置；对DEpopulation中粒子进行变异、交叉、选择操作；

Step4通过fitness函数选出PSOpopulation中的最优粒子PSObest和DEpopulation中的最优粒子DEbest；

Step5对比选出PSObest与DEbest中最优个体，替换次优个体；

Step6判断粒子是否停留某点，若停留，产生新粒子；否则继续下一步；

Step7若没达到最大进化代数，转Step3继续寻优；若达到，则输出最优解，完成寻优计算．

1.3 仿真实验与对比分析

为验证改进算法的寻优性能，采用表1所示的4个经典的国际标准测试函数进行寻优实验与对比分析．

表1 国际标准测试函数Tab.1 Internationalstandard testing functions

表1中的测试函数均可视为由多目标函数转化而成，其中Sphere函数为一简单的单峰函数，通过此函数可以看出不同算法的收敛快慢．Rosenbrock函数也是单峰函数，但其全局最优值不易获得，容易出现早熟现象，通过Rosenbrock函数可以测试算法的计算精度和寻优能力．Rastrigin函数在维数较少的情况下可以看作非线性的多峰函数，存在多个局部极值，因此较难实现寻优；Griewank函数拥有许多局部最优值，若算法的全局搜索能力与逃离局部最优值的能力弱，则难以寻得最优值；这两个函数可以考察算法全局寻优能力．

分别将4个标准测试函数作为适应度函数fitness来求解其最小值，4种算法（DE、RDE、CDE、PSODE）中的相关参数设置为：wmax=0.9，wmin=0.4，c1=c2=2，CR=0.8，F=0.6，k=3，Gp=20代，种群大小设定为100组，最大进化代数Gn=3 000次，优化函数设定为10维．收敛曲线如图1～图4所示，适应度函数fitness的计算结果如表2所示，其中统计了10次测试结果，Best为最好优化值，Worst为最差优化值，Mean为平均值．

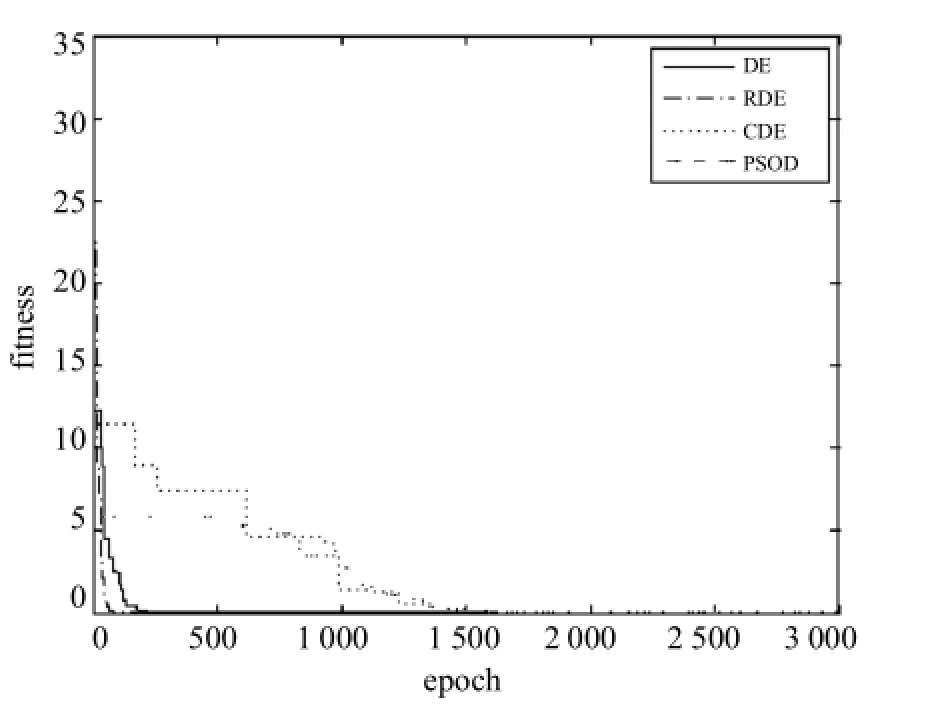
图1 几种算法对Sphere函数的寻优收敛曲线Fig.1 Convergence curves for Sphere function

图2 几种算法对Rosenbrock函数的寻优收敛曲线Fig.2 Convergence curves forRosenbrock function

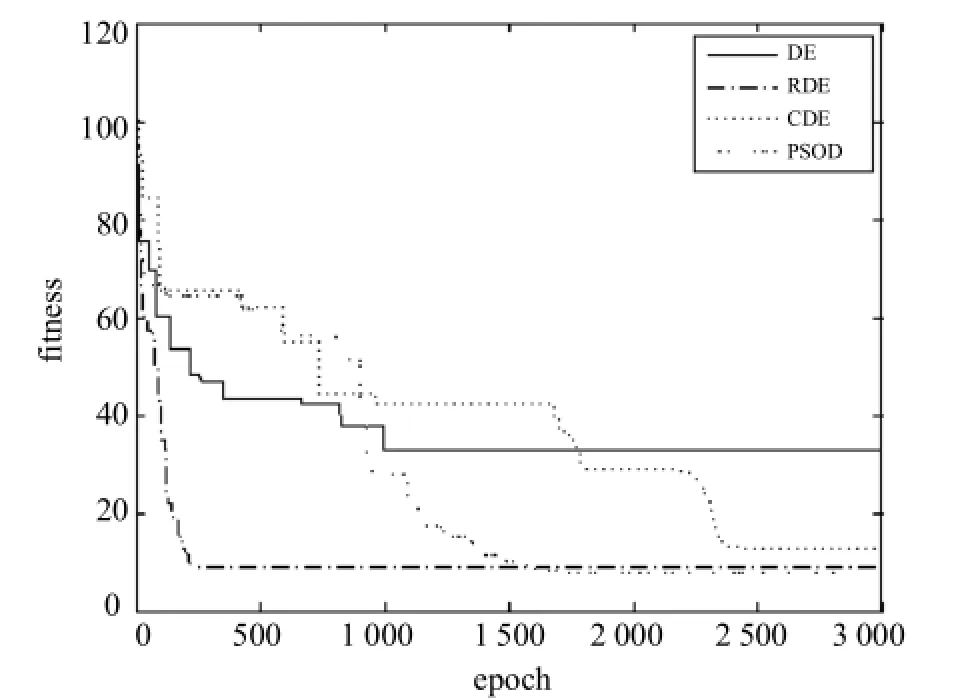
图4 几种算法对Griewank函数的寻优收敛曲线Fig.4 Convergence curves forGriewank function

表2 几种算法的测试效果Tab.2 Testing resultswith fouralgorithms

从图1～图4和表2中发现，DE算法具有较快的收敛速度，在求解低难度优化问题时具有较高的计算精度；RDE加快了算法的收敛速度，但更适用低精度的优化求解；CDE算法表现稳定，收敛速度不快，但是可以求解出高精度的最优解；PSODE算法在收敛速度上比CDE快，但不及DE和RDE，然而在高难度的寻优问题中可以求得高精度解，特别是在计算后期，与DE算法相比，避免计算停滞的能力明显提高，即克服了早熟现象的发生．因此PSODE算法是具有实用价值的．

2 实际应用

在红外搜索系统的应用中，常用钟形波来代替理论上的脉冲信号，因此信号处理器应该产生一个与钟形波相匹配的滤波器，这在实际中是很难实现的．钟形波的函数表达式如下

其中：是波形的半宽度；E是钟形波的高度．经过傅氏变换后的幅频响应为

若想获得与此匹配的滤波器，可以选择与之对应的低通滤波器进行优化设计．其中匹配滤波器可以通过式(14)数字级联方式实现．

其中：A是增益因子；N为级联的级数．在第k级，和均为要优化的参数，可见其滤波器设计即为一个高维优化问题．具体实现方式如图5所示．

设定选择两级级联形式的匹配滤波器，其计算方程可以写为

其中：X是滤波器的输入；Y1和Y2分别是第1级和第2级的输出；W1和W2为加法器的输出．

图5 数字级联滤波器示意图Fig.5 Digital filter in cascade form

在两级级联的滤波器中，频率响应函数为

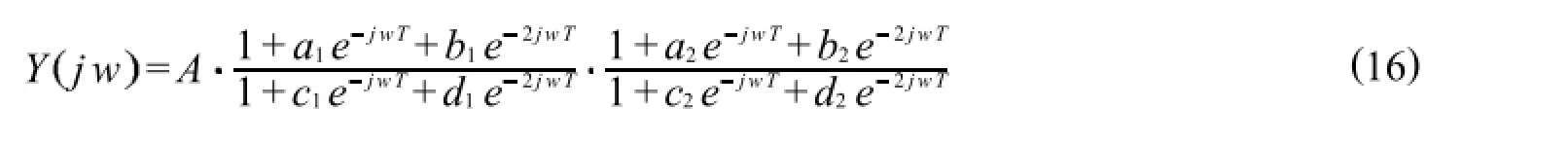
其中=A,a1,b1,c1,d1,a2,b2,c2,d2为一组目标，通过将匹配滤波器频率响应函数与钟形波的频率响应函数对比作为fitness适应度函数

其中：M为离散点个数，则可转化为一个9维的最小值优化问题，参数设置为：wmax=0.9，wmin=0.4，c1=c2=2，CR=0.8，F=0.6，k=3，Gp=20代，种群大小设定为100组，最大进化代数Gn=3000次，=0.15，M=1 000．分别通过DE算法和PSODE算法进行5次寻优得到fitness函数的计算结果如表3所示，PSODE算法所得滤波器参数为

A=0.3531588，a1=1.091 5979，b1=0.747245 2，c1=0.572 1020，d1=0.231006 3，a2=2.5489479，b2=1.861 446 3，c2=0.876 254 1，d2=0.205 392 8．

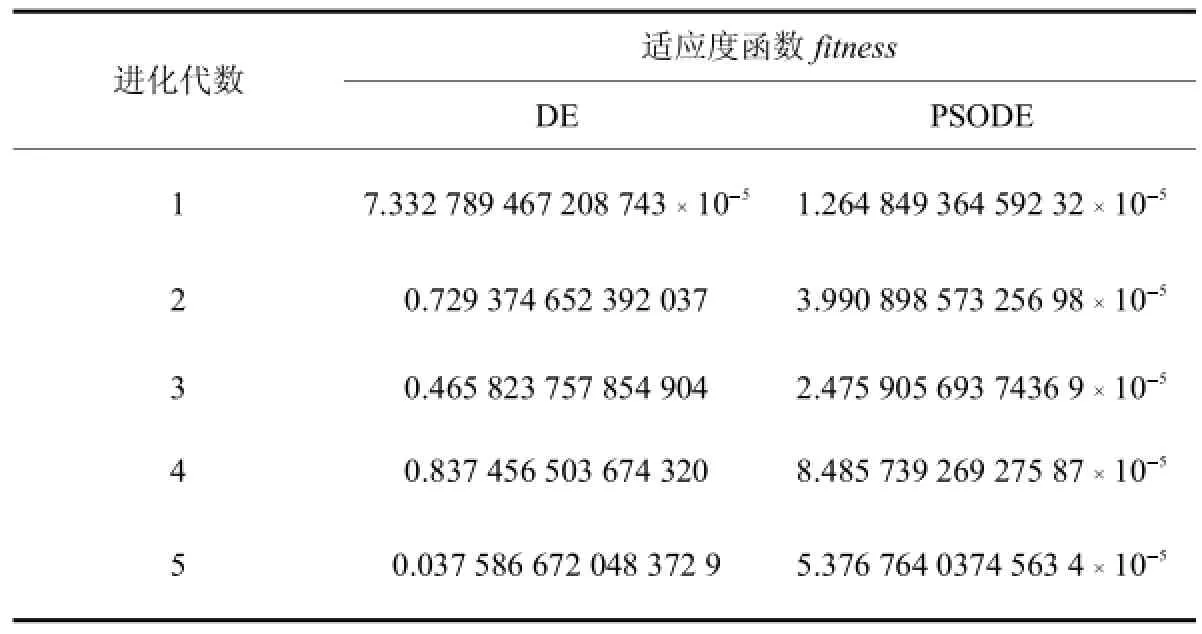
表3 滤波器优化设计效果对比Tab.3 Comparison on filteroptimization design effect

由表3可知，PSODE算法具有很高的计算精度，逃离局部最优值的能力强，减少了早熟现象的发生，因此其寻优计算的稳定性更高．

3 结论

在差分进化算法中，采用随机变异因子可以加快算法的收敛速度，很适用于低精度的优化求解；采用收敛变异因子虽然收敛速度不快，但表现稳定，可以求解出高精度的最优解；而采用基于粒子群优化算法的混合算法（PSODE）在高难度寻优问题中可以求得高精度解，特别是在计算后期可以避免计算停滞等早熟现象，从而提高优化效率．数字滤波器的设计为一个高维函数优化问题，采用差分进化算法能够实现滤波器的优化设计，特别是采用本文改进的混合算法可以取得更为满意的设计效果．

[1]肖晓伟，肖迪，林锦国，等．多目标优化问题的研究概述[J]．计算机应用研究，2011，28（3）：805-808．

[2]马小姝，李宇龙，严浪．传统多目标优化方法和多目标遗传算法的比较综述[J]．电气传动自动化，2010，32（3）：48-50．

[3]Storn R，Pricek．Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces[J]．Technical Report，International Computer Science Institute，1995，9（8）：22-25．

[4]Storn R，Pricek．Differentialevolution-a simple and efficientheuristic for globaloptimization over continuous spaces[J]．Journalof Global Optimization，1997，11（4）：341-359．

[5]AbbassH A，Sarker R，New ton C．A Pareto-frontier differentialevolution approach formulti-objectiveoptimization problems[C]//IEEECongress on Evolutionary Computation．Piscataway，2001，971-978．

[6]Abbass HA，SarkerR．Thepareto differentialevolution algorithm[J]．International Journalon Artificial Intelligence Tools，2002，11（4）：531-552．

[7]Babu BV，Jehan M M L．D ifferentialevolution for M ulti-objective optimization[C]//IEEE Congress on Evolutionary Computation．Canberra，2003，2696-2703．

[8]孟红云，张小华，刘三阳．用于约束多目标优化问题的双群体差分进化算法[J]．计算机学报，2008，31（2）：228-235．

[9]Saber M Elsayed，Ruhul A Sarker，Daryl L Essam．A self-adaptive combined strategies algorithm for constrained optim ization using differential evolution[J]．Applied M athematics and Computation，2014，241：267-282．

[责任编辑 代俊秋]

An improved differentialevolution algorithm and itsapplication

XIA Xin-yuan1，LIU Bo-ying2，LIYang3，LILing-ling3

(1.Schoolof Electronic and Information Engineering,HebeiUniversityofTechnology,Tianjin300401,China;2.SchoolofComputer Scienceand Software,HebeiUniversity ofTechnology,Tianjin 300401,China;3.Schoolof ElectricalEngineering,HebeiUniversity of Technology,Tianjin 300401,China)

Multi-objectiveOptim ization Problem（MOP）isvery common butdifficult to besolved,so ithas im portant significance to solve MOPusing DifferentialEvolution(DE)algorithm.To overcome theshortcom ingsin DEalgorithm, such as the lim ited performance,themutual restriction among convergent rate,com putationalaccuracy and optim ization ability,ahybrid approach to particleswarm optimization(PSO)andDEalgorithm ispresented by improvingmutagenic factor,evolutionism andmixing PSO algorithm.Simulation experimentand comparative analysis on classical testing functionsshow thatthepresented improved approach can get thehigh accuracy solution inhigh dimensionalcomplex optimization problems.In theactualdesign on digital filterby improved approach,theapplication effect can be obtained satisfactory at computationalaccuracy and operation rate.

differentialevolution algorithm;multi-objective optim ization problem;digital filter design

TP18

A

1007-2373(2015)01-0012-07

10.14081/j.cnki.hgdxb.2015.01.003

2014-11-05

国家自然科学基金（51475136）；河北省引进留学人员基金（C2012003038）；国家大学生创新创业训练计划（201310080017）；河北省大学生创新创业训练计划（201310080073）

夏莘媛（1992-），女（汉族），硕士生．通讯作者：李玲玲（1968-），女（汉族），教授，博士生导师．